Математическая игра "Знаток истории математики"

Правила игры «Знаток истории математики»

Игра состоит из 2 раундов и финала. В начале каждого раунда объявляются темы и стоимость вопросов (количество баллов, которые можно получить при правильном ответе на вопрос). Команды по очереди выбирают тему и стоимость вопроса, после чего ведущий зачитывает соответствующий вопрос. Порядок, в котором команды выбирают вопросы, определяется ведущим перед началом игры.

В каждом раунде 4 темы и 3 различных стоимостей вопросов (всего 24 задания) и в финале 3 задачи. Время на обсуждение заданий первого раунда – 2 минуты, 2 раунда – 3 минуты, задание финала – 5 минут. По истечении этого времени все команды сдают бланк с вариантом своего ответа счетной комиссии. В случае правильного ответа команда получает количество очков, равное стоимости вопроса, если она ответила неверно, то теряет количество очков, равное стоимости вопроса. Если команда вообще не дает ответа, то команда на бланке ответов пишет «сброс» и получает 0 баллов.

В финал проходят все команды, набравшие положительное количество баллов. Команды, набравшие наибольшее количество очков имеют право убрать 2 нежелательные задачи, вследствие чего оставшаяся задача является заданием финала. Каждая команда делает свои ставки (ставка не превышает количества набранных баллов). При правильном ответе они получают баллы, равные сумме набранных баллов и ставки. При неправильном ответе - получают баллы, равные разности набранных баллов и ставки.

40

Знаток истории

математики

Продолжить игру

II раунд

Садовникова М.Г. Миронова Л.Н. РС(Я), г.Ленск, Лицей №2

I раунд

Математические

термины

10

20

30

Великие математики

и их теоремы

10

30

20

И нструменты

20

30

10

ЧИСЛА

30

20

10

РАУНД II

математика

10

Математические термины

Назовите слово, которое в переводе с греческого означает

«наука, размышление»

Слово «математика» произошло от греч. мάθημα (мантейнен). В текстах на русском языке слово «математика» или «маѳематика» встречается с XVII века.

Продолжить игру

РАУНД II

аксиома

20

Математические термины

Утверждение, не требующее доказательства или принятое за истину,

на основе которого доказываются другие утверждения

Аксиома (греч. слово axios- ценный; axioma – «принятие положения», «почет», «уважение», «авторитет»). В русском языке – с Петровских времен. Впервые встречаются у Аристотеля. Использовались в книгах Евклида «Начала».

Продолжить игру

РАУНД II

гипотенуза

30

Математические термины

Назовите слово, которое в переводе с греческого означает «натянутая тетива»

Гипотенуза (греч.слово gyipotenusa – «стягивающая»). Заимствовано из латинского языка в 18 в., в котором hypotenusa – (от греч.) сторона прямоугольного треугольника, лежащая против прямого угла. Древнегреческий ученый Евклид писал: «сторона, которая стягивает прямой угол».

Продолжить игру

РАУНД II

Что и требовалось доказать

10

Великие математики и их теоремы

Какой фразой древнегреческого ученого Евклида заканчивается доказательство математического утверждения?

Запишите эту фразу.

Евклид

(IIIв. до н.э). Главный труд, написанный около III в. до н. э., – «Начала». Посвящён систематическому построению геометрии.

Продолжить игру

РАУНД II

Софья Васильевна Ковалевская

20

Великие математики и их теоремы

Кто изображен на портрете?

С.В.Ковалевская

(1850-1891)

Русский математик, механик, писатель и публицист. Автор повести «Нигилистка» (1884).

Продолжить игру

РАУНД II

Решето Эратосфена

30

Великие математики и их теоремы

Как называется алгоритм нахождения простых чисел среди натуральных чисел?

Эратосфен

(IIIв. до н.э) – греческий ученый, астроном, географ, филолог и поэт.

Первый ученый, доказавший, что Земля имеет форму шара.

Продолжить игру

РАУНД II

астролябия

Инструменты

10

Как называется инструмент для измерения углов на местности?

Первая астролябия появилась в Древней Греции. Витрувий в своём писании «Десять книг об архитектуре», рассказывая про астрономический инструмент, называемый «пауком», говорит, что его «изобрёл астроном Евдокс, а иные говорят — Аполлоний».

Продолжить игру

РАУНД II

9

С помощью циркуля и линейки разделить произвольный угол на 3 равные части

Инструменты

20

В чем суть задачи о трисекции угла?

Одной из кривых, открытой в последствии решения задачи, является спираль Архимеда.

Продолжить игру

РАУНД II

Инструменты

30

Как начертить окружность на местности?

Окружность – самая простая из всех кривых линий. Одна из древнейших геометрических фигур. Согласно Аристотелю, небесная материя, из которой состоят планеты и звезды, как самая совершенная, должна двигаться по самой совершенной линии - окружности.

РАУНД II

Продолжить игру

Положительные

и отрицательные

10

Числа

До XVIв., как и в древности, большинство ученых считали эти числа «ложными» и «истинными». О каких числах идет речь?

Термины произошли от слов plus – «больше»,  minus – «меньше». Сначала действия обозначали первыми буквами p, m.

Современные знаки «+» и «-» появились в Германии в последнее десятилетие XVв.  в книге Видмана, которая была руководством по счету для купцов (1489г).

Продолжить игру

РАУНД II

дружественные

20

Числа

Как называют два числа, каждое из которых равно сумме делителей другого числа, не считая самого числа?

Первая пара различных наименьших дружественных чисел 220 и 284 была известна еще древнегреческому ученому Пифагору (6 в. до н.э.). Пифагорейцы считали их символом дружбы.

Продолжить игру

РАУНД II

В IX веке – Сабит ибн Корра нашел общий способ получения дружественных чисел.

1636г. – открытие второй и третьей пары дружественных чисел французским юристом и математиком Пьером Ферма и Рене Декартом.

1747-1750 г. г. – Леонард Эйлер указал сразу 59 пар дружественных чисел.

1867г. (в некоторых источниках 1887г.)– поразительное открытие сделал 16-летний итальянец Никколо Паганини (тезка знаменитого скрипача), обнаружив вторую по величине пару дружественных чисел 1184 и 1210, которую проглядели все знаменитые математики.

3, 5, 8

30

Числа

Продолжите ряд 3 числами: 0, 1, 1, 2,…

Речь шла а размножающихся кроликах, количество которых образовывали последовательность:

0,1,1,2,3,5,8,13,21,34,55,89,...

– числа Фибоначчи

(Леонардо Пизанский). Ученый не подозревал, что задача из его книги обессмертит его имя.

Продолжить игру

РАУНД II

II раунд

Древний Египет

60

40

20

Древний Восток

40

20

60

Древний Рим

40

20

60

Русь

60

40

20

финал

70+(353-128):5+173=288

20

Древний Египет

Запишите пример в египетской системе счисления и решите

Продолжить игру

финал

7;49;343;2401;16807

Сумма –19607

40

Древний Египет

У семи лиц по семи кошек, каждая кошка съедает по семи мышей, каждая мышь съедает по семи колосьев, из каждого колоса может вырасти по семь мер ячменя. Как велики числа этого ряда и их сумма?

Задача из папируса Ринда (папирус с математическими задачами). Написан иератическим древнеегипетским письмом (одна из форм египетского письма).

Продолжить игру

финал

9

60

Древний Египет

Найти число, если известно, что от прибавления к нему его две трети и вычитания из суммы ее трети получается число 10.

Задача из папируса Ринда («папирусом Ахмеса» или папирус Британского Музея). Куплен на Луксорском базаре шотландским любителем древностей Александром Генри Риндом (1833–1863) в 1858 году.

Продолжить игру

финал

2∙60 2 +28∙60+45

20

Древний Восток

Запишите число 8925 в вавилонской системе счисления

Продолжить игру

финал

23

40

Древний Восток

Имеются вещи, число их неизвестно. Если считать тройками, то остаток 2; если считать пятерками, то остаток 3; если считать их семерками, то остаток 2.

Спрашивается, сколько вещей.

Задача Сунь-цзы (III-IVвв) – китайский математик. Сформулировал правило действий на счетной доске.

Продолжить игру

финал

60

Древний Восток

Решить уравнение в целых числах

Задача Бхаскары II

(1114 г. – позднее 1178 г.) – крупнейший индийский математик и астроном. Вершиной достижений является циклический метод решения в целых положительных числах.

Продолжить игру

финал

[1325-(1439-226)]:4=28

Древний Рим

20

Запишите пример в римской системе счисления и решите его.

Продолжить игру

финал

сын:жена:дочь

4:2:1

40

Древний Рим

Некто, умирая, завещал: «Если у моей жены родится сын, то пусть ему будет имения, а жене – остальная часть. Если же родится дочь, то ей – , а жене – остаток».

Родилась двойня – сын и дочь.

Как разделилось имение?

Древнеримская задача (IIв.)

Продолжить игру

финал

;

Древний Рим

60

Один говорит другому: «Дай мне 7 динариев, и я буду в 5 раз богаче тебя». А другой говорит: «Дай мне 5 динариев, и я буду в 7 раз богаче тебя».

Сколько динариев у каждого?

Задача Леонардо Пизанского (1180-1240). Леонардо имел прозвище Фибоначчи,

т.е. «сын Боначчо» (добродушный).

Продолжить игру

финал

1325:25+246=299

: + =

20

Русь

Решите и запишите пример

в славянской нумерации

1325:25+246

финал

Продолжить игру

35

40

Русь

Один человек выпьет кадь пития в 14 дней, а с женою выпьет ту же кадь в 10 дней. И ведательно есть, в колико дней жена его особенно выпьет ту же кадь.

Задача Л.Ф.Магницкого (1669-1739)

(из учебника «Арифметика»), русского математика, педагога. Молодым он произвёл на царя Петра I сильное впечатление незаурядным умственным развитием и обширными познаниями.

Продолжить игру

финал

36

60

Русь

Спросил некто учителя: «Скажи, сколько у тебя в классе учеников, так как я хочу отдать к тебе в учение своего сына». Учитель ответил: «Если придет еще столько же, сколько имею, и полстолько, и четвертая часть, и твой сын, тогда у меня будет учеников 100». Спрашивается, сколько было у учителя учеников?

«Арифметика» Магницкого создавалась как учебник для будущих офицеров армии и флота, обучавшихся в Школе навигацких и математических наук. 

Продолжить игру

финал

ФИНАЛ

Печать Соломона

1.

Своя

_

2.

Точки в ряду

игра

Задача о разрезании шахматной доски

3.

Сколько равносторонних треугольников изображено на знаменитой печати царя Соломона, изображенной на его гробнице?

Ответ: 31

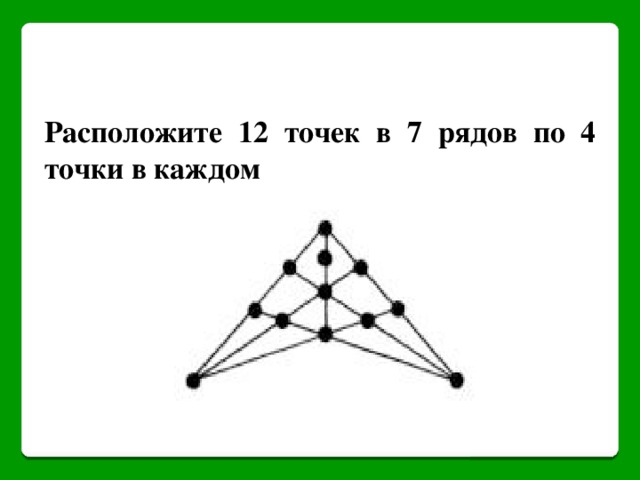
Расположите 12 точек в 7 рядов по 4 точки в каждом

Как мудрецы разделили шахматную доску с алмазами на четыре одинаковые части с одним алмазом в каждой?