Контрольная работа по теме "Применение производной к исследованию функций"

Контрольная работа № 3

«Применение производной к исследованию функции»

Вариант 1.

1. Исследовать на монотонность функцию и найти её экстремумы:

y=2x³ + 3x² – 1

2. Найти промежутки выпуклости функции y = 12x² - x³

3 . Найдите наибольшее значение функции  у= х³-6,5х² +14х-14  на отрезке  [-4; 3]

4.  На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции  , опре­де­лен­ной на ин­тер­ва­ле  . Най­ди­те про­ме­жут­ки воз­рас­та­ния функ­ции  . В от­ве­те ука­жи­те сумму целых точек, вхо­дя­щих в эти про­ме­жут­ки.

5. На ри­сун­ке изоб­ражён гра­фик y=f'(x) — про­из­вод­ной функ­ции f(x), опре­де­лен­ной на ин­тер­ва­ле (-8; 3). В какой точке от­рез­ка [-3; 2 ] функ­ция f(x) при­ни­ма­ет наи­боль­шее зна­че­ние?

6. Построить график функции, предварительно исследовав ее по алгоритму:

у=2х³-3х² +1

Алгоритм исследования функции:

1.Область определения функции D(f)

2.Четность/нечетность, периодичность

3. Точки пересечения графика с осями координат

4.Промежутки монотонности функции

5.Экстремумы функции

6.Промежутки выпуклости и точки перегиба

7.Асимптоты функции

8. Дополнительные точки

Дополнительно:

7. Представьте число 42 в виде суммы трех положительных слагаемых так, чтобы два из них были пропорциональны числам 2 и 3, а произведение всех слагаемых было наибольшим.

Контрольная работа № 3

«Применение производной к исследованию функции»

Вариант 2.

1. Исследовать на монотонность функцию и найти её экстремумы:

y=3x³ + 2x² – 14

2. Найти промежутки выпуклости функции y = 6x² - x⁴

3. Найдите наименьшее значение функции  у= х³-х² -40х+3  на отрезке  [0; 4]

4 .  На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции f(x), опре­де­лен­ной на ин­тер­ва­ле (−7; 14). Най­ди­те ко­ли­че­ство точек мак­си­му­ма функ­ции f(x) на от­рез­ке [−6; 9]. 

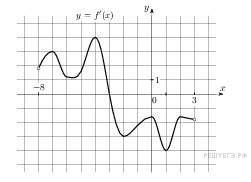
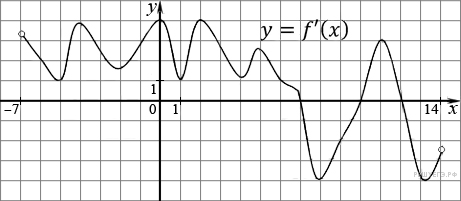
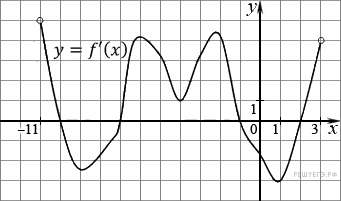5 .На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции f(x), опре­де­лен­ной на ин­тер­ва­ле (−11; 3). Най­ди­те про­ме­жут­ки воз­рас­та­ния функ­ции f(x). В от­ве­те ука­жи­те длину наи­боль­ше­го из них.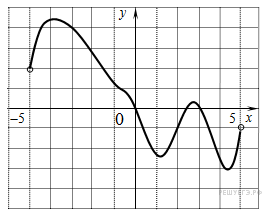

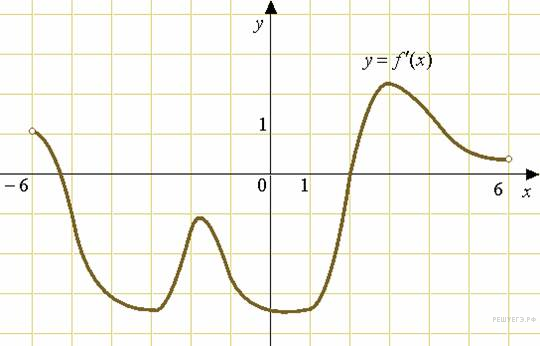
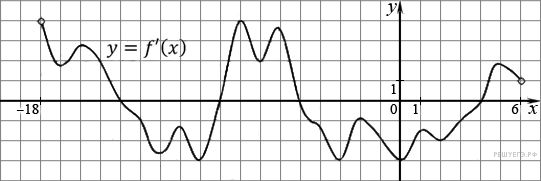6. Построить график функции, предварительно исследовав ее по алгоритму:

у=-2х³+3х² -1

Алгоритм исследования функции:

1.Область определения функции D(f)

2.Четность/нечетность, периодичность

3. Точки пересечения графика с осями координат

4.Промежутки монотонности функции

5.Экстремумы функции

6.Промежутки выпуклости и точки перегиба

7.*Асимптоты функции

8. Дополнительные точки

Дополнительно:

7. Представьте число 45 в виде суммы трех положительных слагаемых так, чтобы два из них были пропорциональны числам 1 и 4, а произведение всех слагаемых было наибольшим.

Контрольная работа № 3

«Применение производной к исследованию функции»

Вариант 3.

1. Най­ди­те точку мак­си­му­ма функ­ции .

2. Найти промежутки выпуклости функции

3. Най­ди­те наи­боль­шее зна­че­ние функции   на

от­рез­ке  .

4.  На ри­сун­ке изоб­ра­жен гра­фик функ­ции  , опре­де­лен­ной на ин­тер­ва­ле (−5; 5). Опре­де­ли­те ко­ли­че­ство целых точек, в ко­то­рых про­из­вод­ная функ­ции   от­ри­ца­тель­на.

5 . На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции f(x), опре­де­лен­ной на ин­тер­ва­ле (−18; 6). Най­ди­те ко­ли­че­ство точек ми­ни­му­ма функ­ции f(x) на от­рез­ке [−13;1].

6. Построить график функции, предварительно исследовав ее по алгоритму:

у=х³-2х² +х

Алгоритм исследования функции:

1.Область определения функции D(f)

2.Четность/нечетность, периодичность

3. Точки пересечения графика с осями координат

4.Промежутки монотонности функции

5.Экстремумы функции

6.Промежутки выпуклости и точки перегиба

7.Асимптоты функции

8. Дополнительные точки

7. Дополнительно: Из всех прямоугольных параллелепипедов, у которых в основании лежит квадрат и площадь полной поверхности равна 600 см², найти параллелепипед наибольшего объема (записать его измерения).