Обобщающий урок в 10 классе по теме «Производная функции»
Девиз урока: Решай, ищи, твори и мысли. И в задачах тех ищи удачу, где получить рискуешь сдачу! (Ритм)
Тип урока: обобщения и систематизации
Дидактическая цель: создать условия для систематизации изученного материала, выявления уровня овладения системой знаний и умений, опытом творческой деятельности средствами информационно – коммуникационной технологии.
Задачи:
Образовательная: обобщить и систематизировать изученный материал по теме «Производная функции, выяснить степень готовности учащихся к контрольной работе.
Развивающая: способствовать формированию ключевых компетентностей, развитию элементов творческой самостоятельной деятельности учащихся, внимания, наблюдательности.
Воспитательная: воспитание устойчивого интереса к изучению математики через применение различных видов деятельности на уроке, толерантности, культуры речи, уверенности в себе, ответственности за качество и результат выполняемой работы на уроке.
Формы организации учебной деятельности: фронтальная, групповая, индивидуальная.
Методы: проблемный, частично – поисковый, исследовательский.
Форма урока: игровая «Самая умная пара по математике»
Оборудование: компьютер, проектор, интерактивная электронная доска ACTIVboard, электронный карандаш ACTIVpen, тестирующие устройства ACTIVote, флипчарты, раздаточный материал.
Планируемый результат урока: Учащиеся должны знать правила нахождения производных и быть готовыми к выполнению контрольной работы, отработать навыки применения теоретических знаний расчета производной функции на учебных примерах, почуствовать ответственность за качество и результат выполняемой работы на уроке.
Ход урока:
Организационный момент
Объявление девиза урока (Флипчарт 1)
Постановка целей и задач урока
2) Повторение теоретического материала (1 балл)
1. Сформулировать достаточный признак возрастания (убывания) функции:
Теорема 3 (достаточные условия экстремума). Пусть функция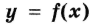 непрерывна на промежутке X и имеет внутри промежутка стационарную или критическую точку
непрерывна на промежутке X и имеет внутри промежутка стационарную или критическую точку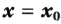 . Тогда:
. Тогда:
а) если у этой точки существует такая окрестность, в которой при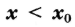 выполняется неравенство
выполняется неравенство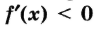 , а при
, а при — неравенство
— неравенство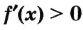 , то
, то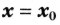 — точка минимума функции
— точка минимума функции 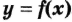 ;
;
б) если у этой точки существует такая окрестность, в которой при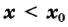 выполняется неравенство
выполняется неравенство  , а при
, а при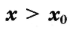 — неравенство
— неравенство 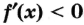 , то
, то 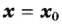 — точка максимума функции
— точка максимума функции 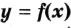 ;
;
в) если у этой точки существует такая окрестность, что в ней и слева и справа от точки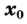 знаки производной одинаковы, то в точке
знаки производной одинаковы, то в точке 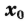 экстремума нет.
экстремума нет.

2. Знак производной меняется по схеме, изображенной на рисунке: (Флипчарт 2)
_ + _ _ +





-6 0 1 3
Определите, на каких промежутках функция возрастает, и на каких убывает.
3.На рисунке изображён график дифференцируемой функции, определите знак производной функции на промежутках. А) [-6;-2) b) (-2;3) c) (3;5] (Флипчарт 3)



- 6 -5 -4 -3 -2 -1 0 1 2 3 4 5
Ответ: плюс, минус, плюс
3.Скажите, что это за алгоритм? (Флипчарт 4) Используется инструмент Шторка. Закрывается название. По тексту алгоритма учащиеся должны определить, алгоритм нахождения исследования функции



«Найди меня» Каждый учащийся выбирает себе пару, в ходе выполнения задания на интерактивной электронной доске ACTIVboard,, соединяя электронным карандаш ACTIVpen функцию и производную. (Флипчарт 5)
.Установите соответствие:
| Функция | 1. 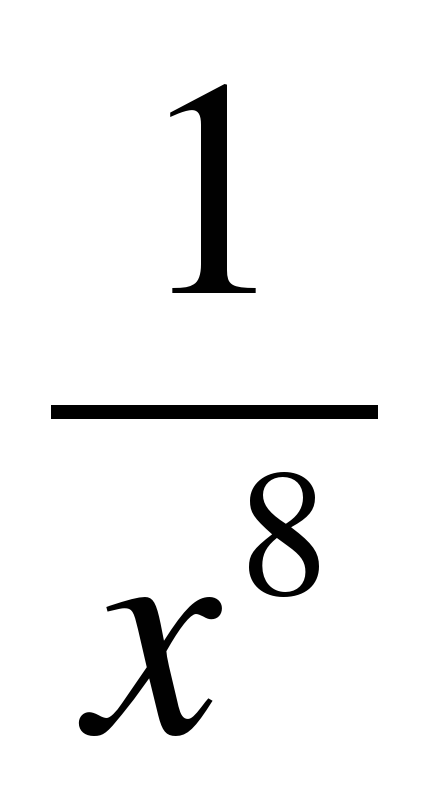 +2 +2 | 2. x+cosx | 3. sin2x | 4. cos2x | 5. 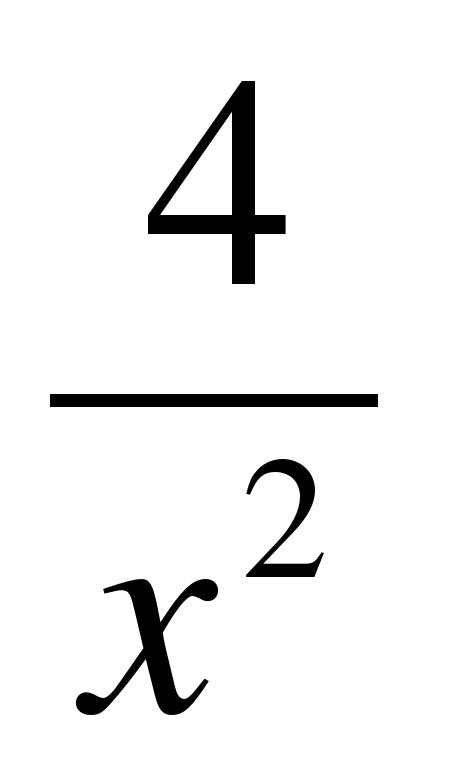 |
|
|
|
|
|
|
|
| Производная | А. 1-sinx | B.  | C. -2sin2x | D. sin2x | E. 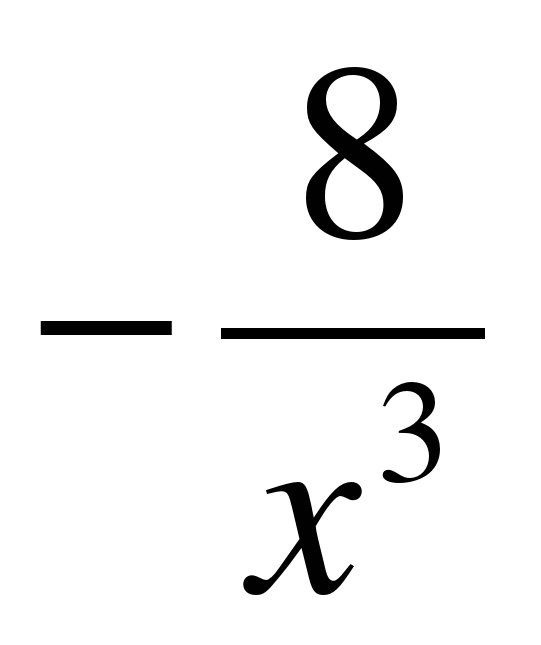 |
5. «Собери слово»
Найдите наибольшее и наименьшее значения заданной функции на заданном отрезке:
Учащиеся получают раздаточные карточки с заданиями
1 . пара 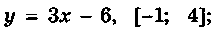 В
В
2. пара 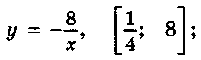 Е
Е
3 пара 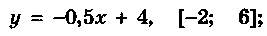 Р
Р
4 пара 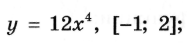 Н
Н
5 пара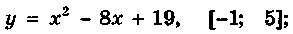 О
О
Слово: ВЕРНО
6 «Самый зоркий» (Флипчарт 6-10)
Найди верный ответ
(Флипчарт 6) Из предложенных вариантов ответов выберите промежутки (промежуток), на которых функция, график которой изображен на рисунке, убывает.
*1) 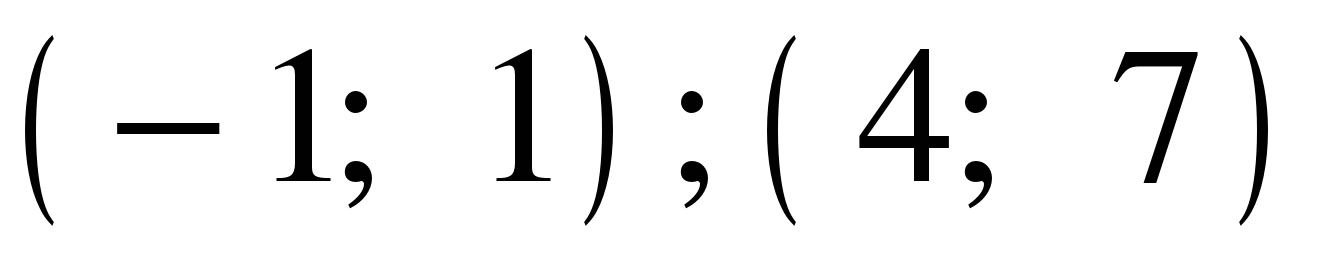
2) 
3) 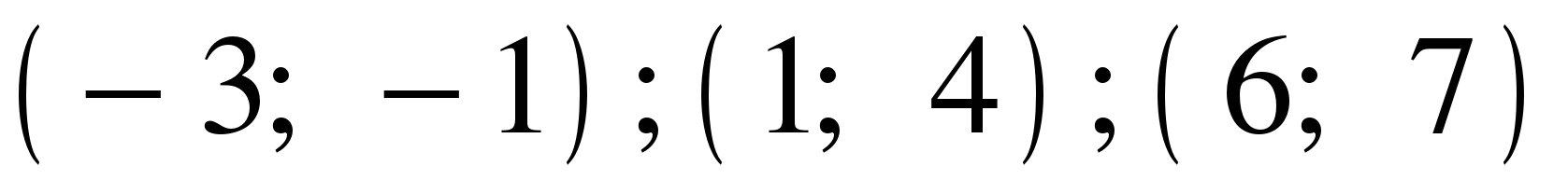
4) 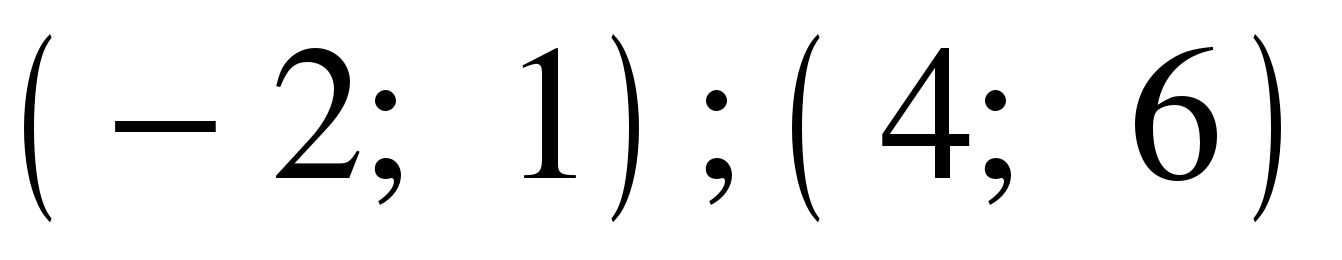

(Флипчарт 7) Из предложенных вариантов ответов выберите промежутки (промежуток), на которых функция, график которой изображен на рисунке, возрастает.

(Флипчарт 8) Из предложенных вариантов ответов выберите промежутки (промежуток), на которых функция, график которой изображен на рисунке, убывает.
(Флипчарт 9) Из предложенных вариантов ответов выберите промежутки (промежуток), на которых функция, график которой изображен на рисунке, убывает.
(Флипчарт 10) Из предложенных вариантов ответов выберите промежутки (промежуток), на которых функция, график которой изображен на рисунке, убывает.
«Самый ловкий» Учащимся раздаются карточки с заданиями
Составьте уравнение касательной к графику функции в точке с абсциссой , если:
, если:
№1
Отв:
№2
Отв::
№3
Отв:
№4
Отв:
№5
Отв:
«Самый быстрый». Флипчарт 11-14
Флипчарт 11
Используя данные о производной, приведенные
в таблице, укажите промежутки возрастания функции
ОТВ:
Флипчарт 12
Используя данные о производной, приведенные в таблице, укажите промежутки убывания функции;
ОТВ
Флипчарт 13
Используя данные о производной, приведенные в таблице, укажите точки максимума функции;
ОТВ: -5
Флипчарт 14
Используя данные о производной, приведенные в таблице, укажите точки минимума функции
ОТВ:-2
9 «Самый экстремальный». Учащимся раздаются карточки
Найдите точки экстремума заданной функции и определите их характер:
№1 ;
ОТВ: x = –2 точка минимума
x = 2 точка максимума
№2;
ОТВ точка максимума
точка максимума
 точки минимума
точки минимума
№3;
ОТВ: точка максимума
точка максимума
 точка минимума
точка минимума
№4
ОТВ: точка максимума
точка максимума
 точки минимума
точки минимума
№5;
ОТВ: х = -2 — точка максимума,
х = 2 — точка минимума
10 «Зри в ответ» Тестирование на интерактивной доске, с помощью тестирующих устройств ACTIVote. Подготовка к ЕНТ.
1. Средняя линия трапеции равна 7 см. Одно из ее оснований больше другого на 4 см. Найти основания трапеции.
А) 10 см, 4 см. В) 5 см, 6 см. C) 5 см, 9 см. D) 11 см, 3 см. Е) 2 см, 12 см.
2. Вычислите
А) -4805/2054. В) 48/20. C) 48,05. D) 0. Е) 1.
3. Решить систему уравнений:
А) (3; 1); (-1; -2). В) (-1; -2); (2; 1). C) (2; 1). D) (-1; -2). Е) (3; 1).
4. Найдите три числа, из которых второе больше первого настолько насколько третье больше второго, если известно, что произведение двух меньших чисел равно 85, а произведение больших равно 115.
А) 8,5; 9; 12. В) 9,1; 3; 4. C) 5; 7; 9. D) 8,5; 10; 11,5. Е) 12; 11; 10.
5. Решите уравнение = 99.
А) 1; 3. В) -1; 3. C) -1; 1. D) 10; 2. Е) -1/10; 1.
6. Найдите самое наименьшее решение неравенства 0.
A) 0. B) 1. C) -1. D) -2. E) 2.
7. Вычислите: 508423 + 5084 + 9765084.
А) 508400. B) 58400 C) 5084. D) 585000. E) 5084000.
8. Упростить выражение ++ .
А) 2. В) 1. С) 0. D) 6. E) 4.
9. В равнобокой трапеции высота, проведенная из вершины тупого угла делит большее основание трапеции на отрезки 6 см и 30 см. Найдите основания трапеции.
A) 26 см и 34 см; B) 12 см и 24 см; C) 24 см и 36 см; D) 41 см и 20 см; E) 22 см и 32 см.
10. Решите уравнение 8b2 + 14 = 32b
A) 0,5; 3,5. B) -0, 5; 3,5. C) 0,5; -3,5. D) 0; 3,5. E) -3,5; -0,5.
Ответы:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| С | А | С | Д | С | А | Е | С | С | А |
11 Домашнее задание: повторить, подготовиться к контрольной работе
12 Итог урока: Выявление типичных ошибок учащихся, их затруднения, выставление оценок.
13 Рефлексия
Самоанализ урока: Урок проведён в 10 классе. Всего в классе 17 учащихся. На уроке присутствовало 17. Урок взят с раздела программы «Производная», по теме «Применение производной». На данном уроке использованы: игровая технология, компьютерное и интерактивное оборудование. Главная цель и задачи урока были достигнуты за счёт самостоятельного поиска и осмысления дополнительного материала во время игры. Игровую форму при моделировании урока я выбирала, исходя их типа и задач урока. На уроке реализованы принципы научно-технического образования, обеспечено развитие познавательной деятельности учащихся с помощью игровой технологии. Данный урок является наглядным примером моей методической работы по теме: «Учебно-тренировочные материалы и новые информационные технологии в изучении математики». Были выполнены задания на выявление самой лучшей пары по математике, предварительно был проведён отборочный тур, в ходе игры учащиеся получали жетоны. Были использованы компьютер, проектор, интерактивная электронная доска ACTIVboard, электронный карандаш ACTIVpen, тестирующие устройства ACTIVote, красочные флипчарты и раздаточный материал. На уроке была проведена работа по подготовке учащихся 10 класса к ЕНТ. В ходе тестирования учащиеся использовали нисколько вычислительные навыки, а в большей степени научились применять другие нетрадиционные методы решения с рациональным использованием времени. Урок очень понравился детям они смогли проявить себя в неординарной ситуации, повторить, показать и обобщить свои знания. Уроки такого вида развивают в детях чувство ответственности и сопереживания за деятельность каждого, а применение интерактивных технологий вызывает познавательный интерес к изучению математики.


























