б) развивающие: способствовать развитию умения анализировать и делать выводы, развивать внимание, мышление, познавательный интерес;
| 1. ТИТУЛЬНЫЙ СЛАЙД | Тема «Диалог математики и музыки» Цитата: Музыка – это радость души, которая вычисляет, сама того не замечая. ( Лейбниц) |
| Организационный момент. СЛАЙД 2
| - У. Здравствуйте ребята! Мы, начиная с февраля месяца в рамках недели математики, провели исследования связей математики с различными науками. Делали проекты Математика+Литература, Математика+ИЗО, Математика+Физ-ра, Математика+История, Математика+Природоведение (учитель обращает внимания учащихся на выставочные проекты). На протяжении этой работы мы убедились в том, что математика – царица наук. И сегодня мы еще раз докажем это утверждение, рассмотрев связь математики и музыки. Это будет необычный урок, а интегрированный. Для этого нам помогут знания по теме «Обыкновенные дроби». |
| Разминка. СЛАЙД 3 | - У. М. Для того чтобы начать любое дело нужно настроиться. В музыке для этого используют инструмент под названием КАМЕРТОН. Если стукнуть им обо что-нибудь, то услышишь нежное и тихое «Ля – а – а». Звук ЛЯ (в музыке) словно маяк, по которому ориентируются композиторы, дирижеры, певцы и многие другие. - МАТЕМАТИКА – точная наука, любит во всем порядок! А музыка не переносит фальши! - У. Итак, настроились на работу, проведем небольшую разминку. Назовите дроби. 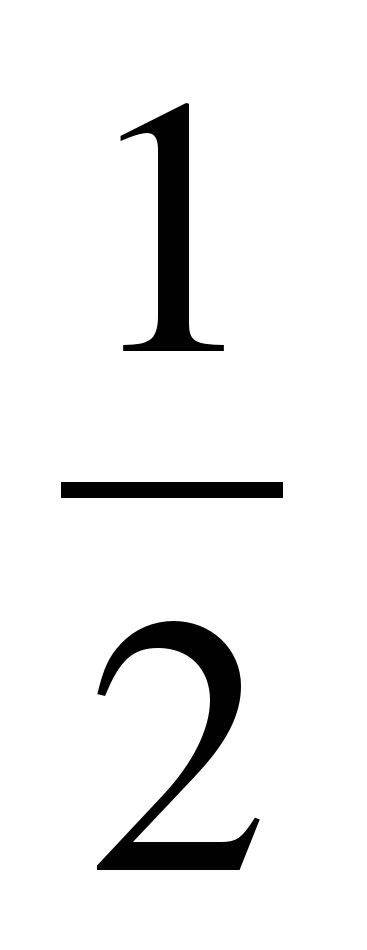 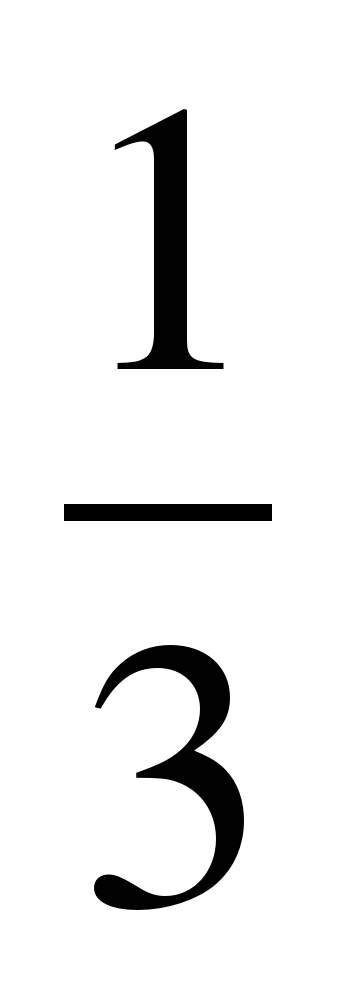 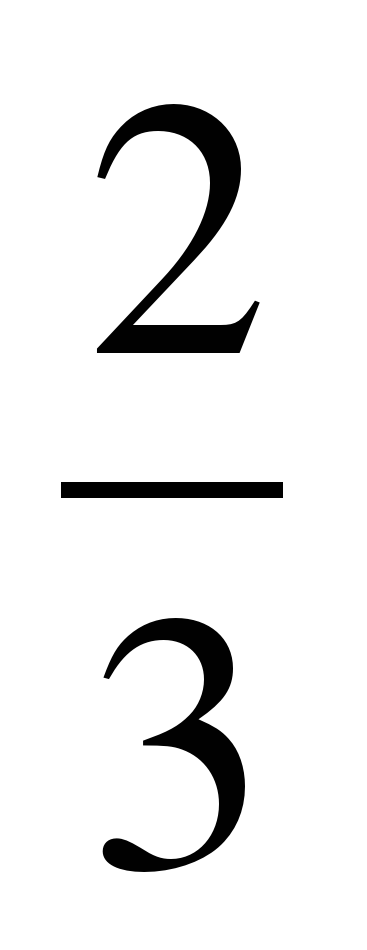 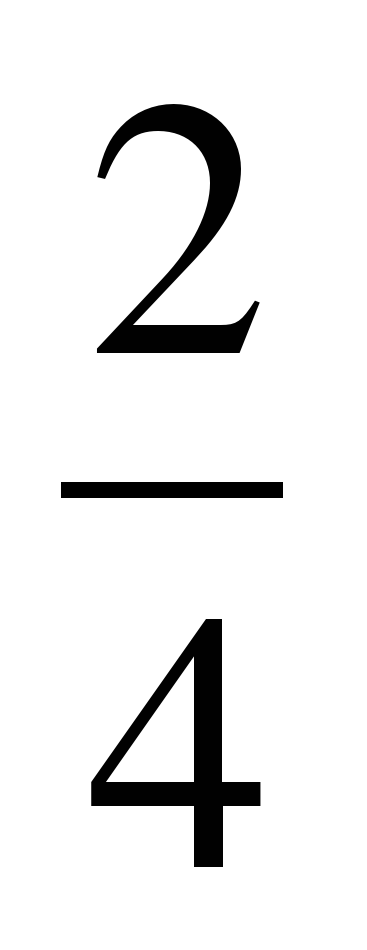 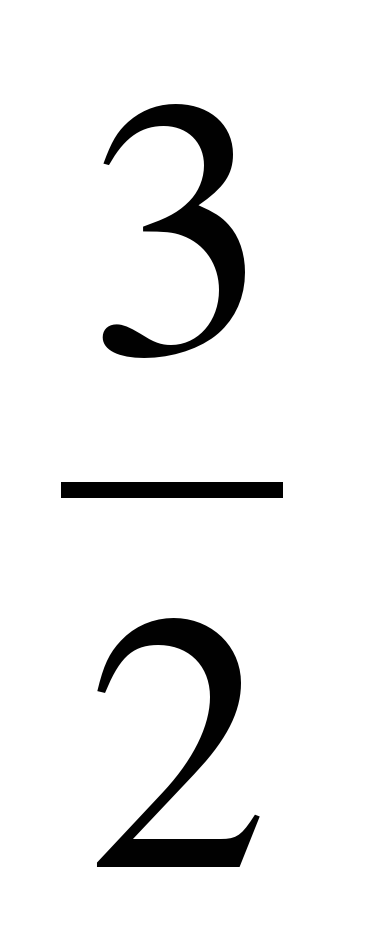 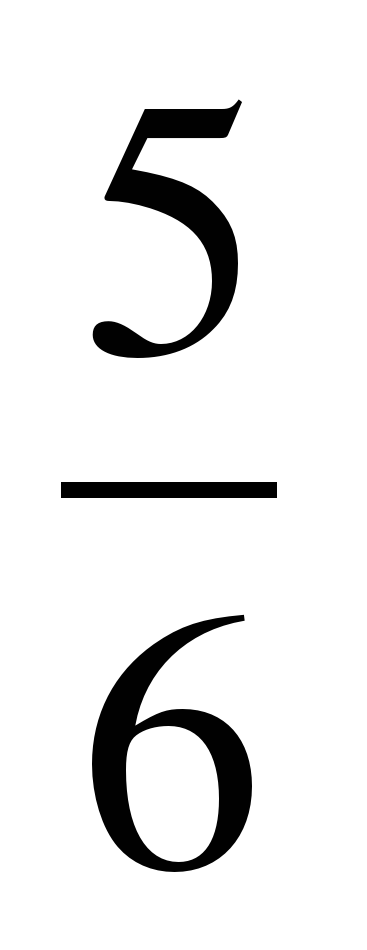 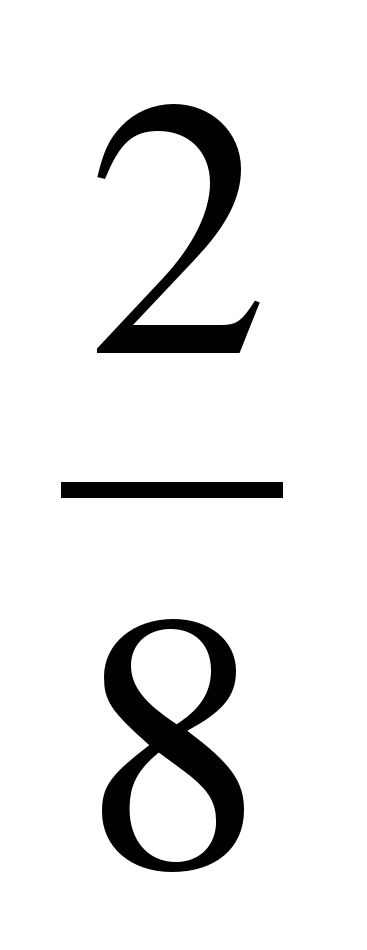 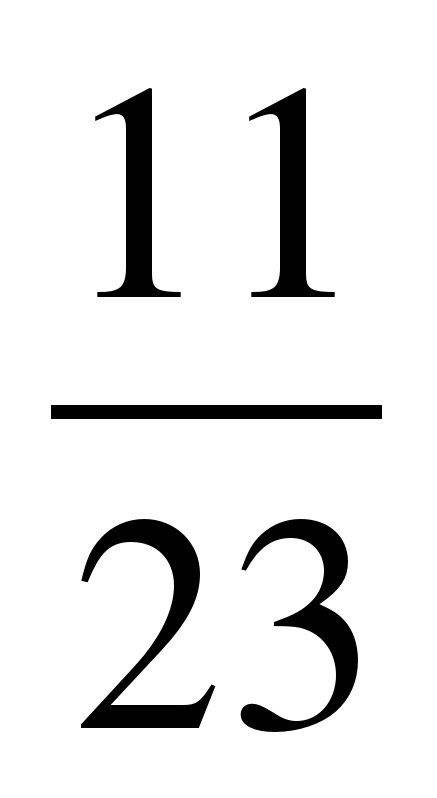 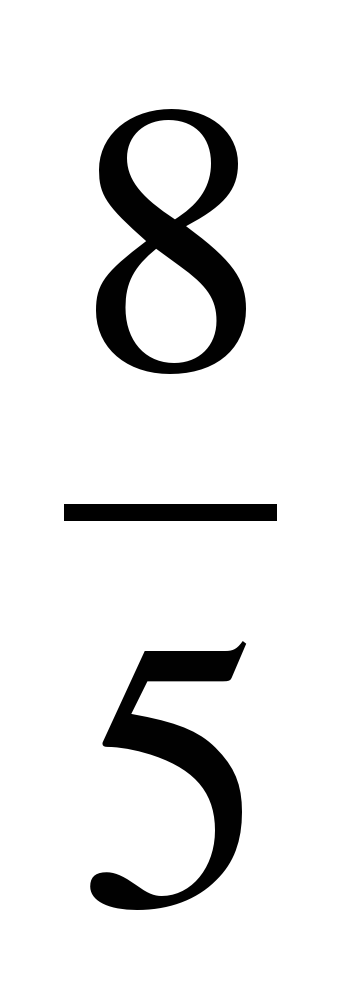 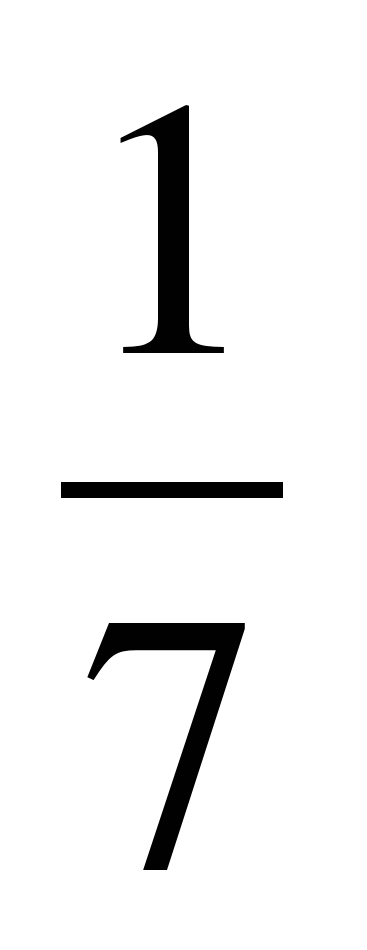 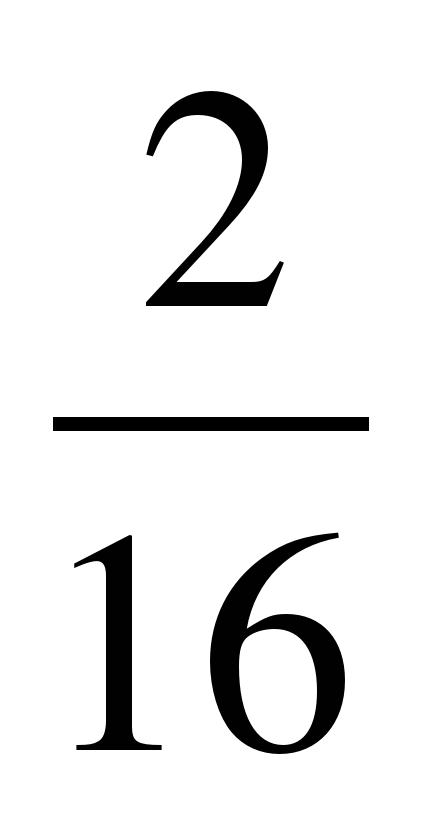 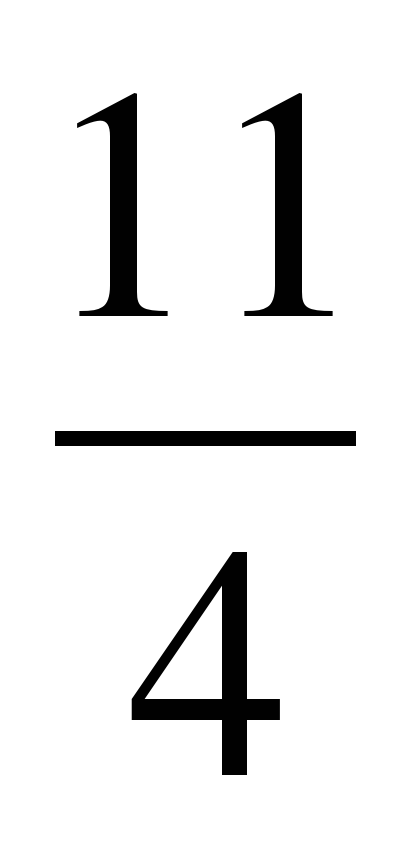 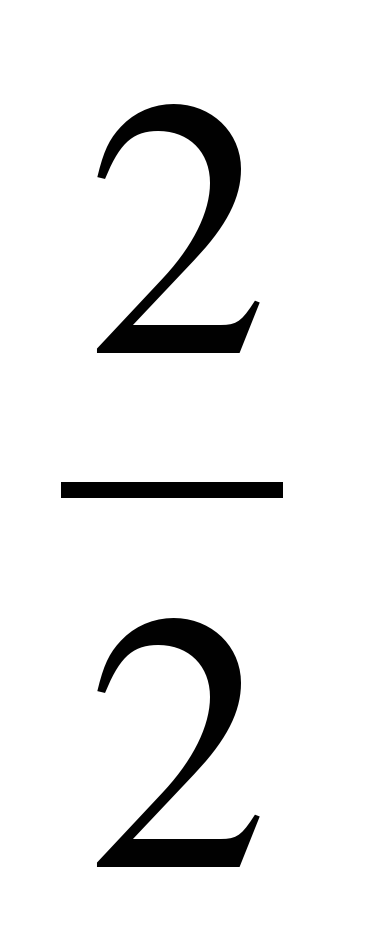 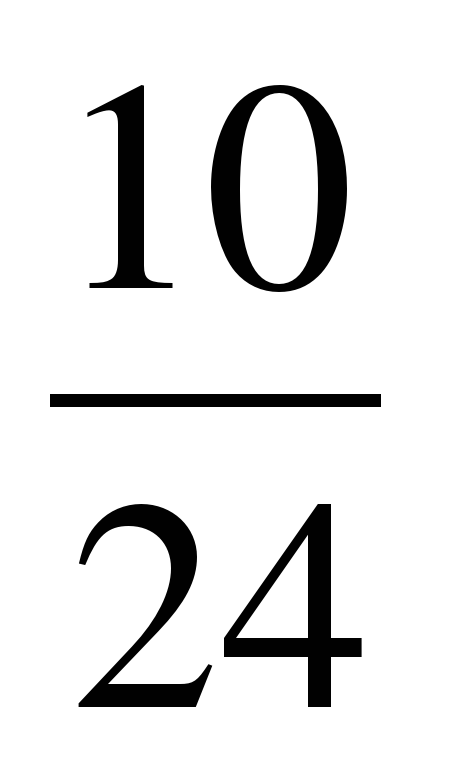 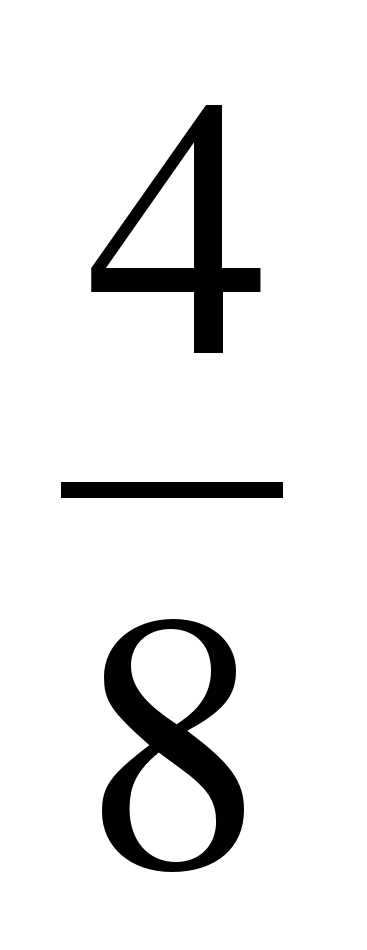 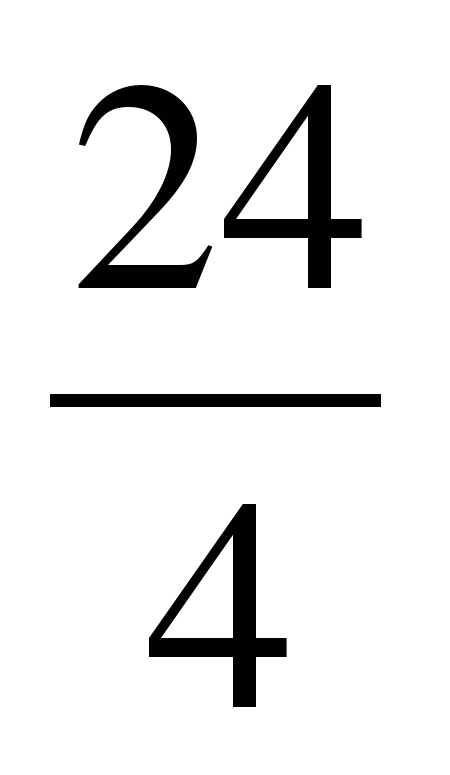 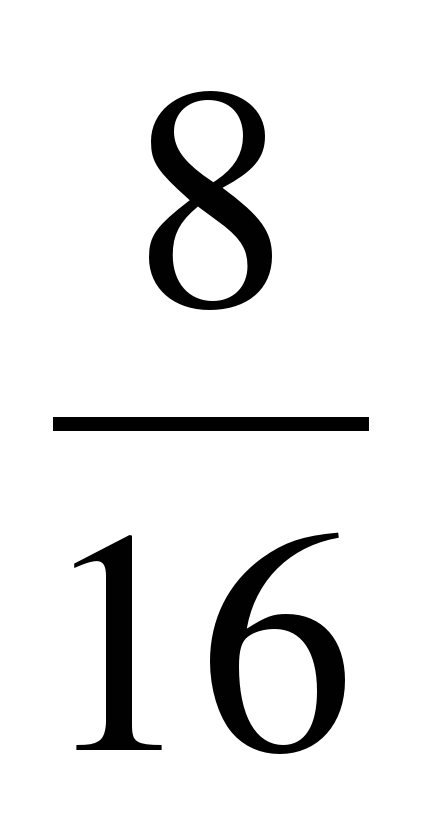 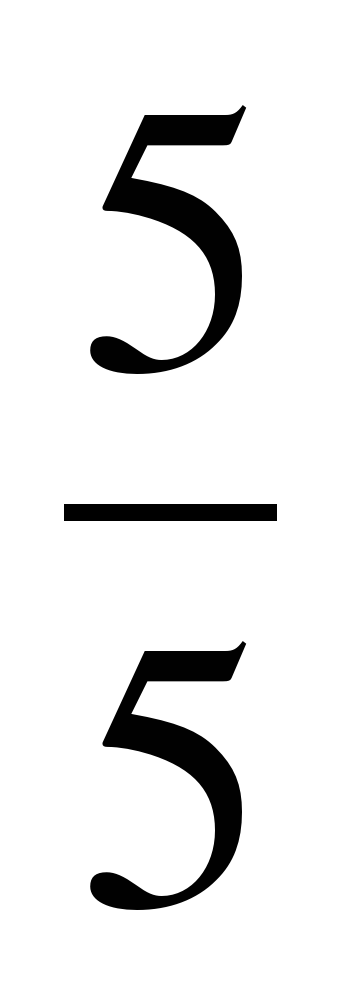 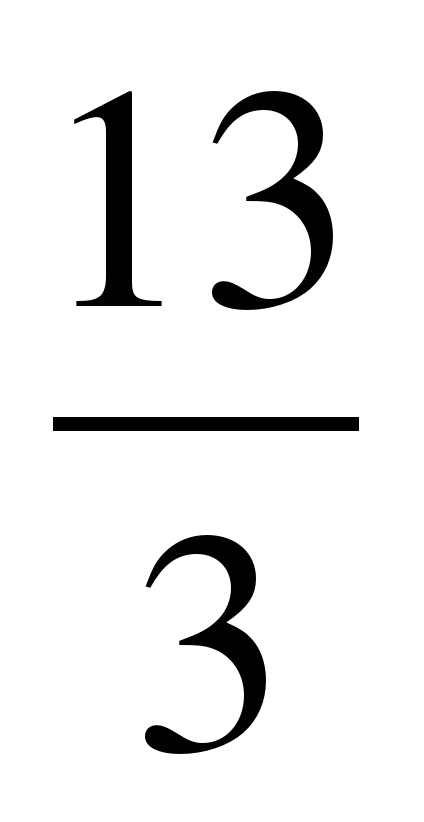 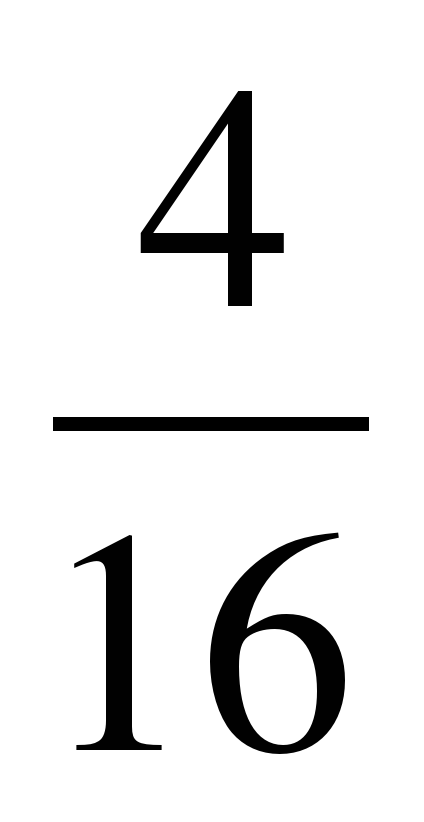 - Назовите неправильные дроби. - Назовите дроби, которые можно заменить натуральным числом. - Назовите дроби половинки. - Назовите дроби четверти. - Назовите дробь, означающую восьмую часть целого. |
| Постановка цели урока. СЛАЙДЫ 4,5
| - У. Тема нашего урока «Диалог математики и музыки» (Заполнить бланки) - Что такое диалог? (Диалог – это взаимосвязь двух или нескольких объектов и их отношения) - Люди уже очень давно задумывались о связи музыки и математики. Давайте, путем несложных вычислений узнаем фамилию ученого, который с помощью математических умозаключений доказал связь двух наук. - Перед вами таблица с числовым рядом.
Данному числовому ряду соответствует буквенный, который поможет нам узнать фамилию ученого. Но использовать мы будем не все буквы, а только те, которые соответствуют следующим числам: (устный счёт) | Ф | Б | О | Г | М | П | И | А | | 6 | 2005 | 80 | 62 | 1790 | 70 | 27 | 24 | | Одна пятая от 350 | 70 | П | | 1% от 2700 | 27 | И | | Две третьих от 9 | 6 | Ф | | Три четвёртых от 32 | 24 | А | | Две десятых от 310 | 62 | Г | | Одна девятая от 720 | 80 | О |
- Да, таинственный незнакомец – древнегреческий философ-математик Пифагор Самосский. А какое математическое правило помогло нам это узнать? (Чтобы найти часть от числа – нужно число разделить на знаменатель и умножить на числитель). - Пифагор Самосский жил в 6 веке до нашей эры. Он изучал интервалы, открывал математические соотношения между отдельными звуками, он развил учение о врачевании болезней при помощи музыки. -Он считал, что определённые мелодии могут избавить человека от ревности, зависти и гордыни. - Именно в музыке он нашел прямое доказательство своему знаменитому тезису «Всё есть число». - А другой известный учёный – Альберт Эйнштейн сказал, что «Настоящая наука и настоящая музыка требуют однородного мыслительного процесса». Задача нашего урока – доказать, что они правы! |
| Изучаем длительности СЛАЙДЫ 8,9 | - У: Ребята, при записи мелодии , звуки имеют свою длину (длительность). В музыке длительности составляют основу любого ритма. Длительности получаются также как и дроби: они возникают при делении целой на равные доли. У. Муз.: (говорит о счете в музыке) У:. Поэтому длительности можно подсчитывать как дробные числа. (рассмотрим схему и заполним таблицу на бланках). | музыка | математика | Длительности | | Целая нота | 1 |  | | Половина целой ноты - половинная | 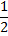 | 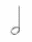 | | Делим целую ноту на 4 части - четвертная |  | 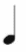 | | Делим целую ноту на 8 частей - восьмая |  | 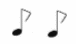 | | Делим целую ноту на 16 частей - шестнадцатая | 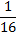 | 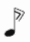 |
- Сколько в целой ноте половинных? Четвертных? Восьмых? Шестнадцатых нот? - Сколько в половинной ноте четвертных? Восьмых? Шестнадцатых нот?
|
| Выполнение заданий СЛАЙДЫ 10-13
| Выполняем задания на бланке. Поставьте знаки �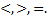 � � Каждую из сумм переведите на язык длительностей. Запишите с помощью чисел равенства и объясните их справедливость. Представьте данную запись в виде суммы и найдите ее значение. |
| Стучим ритм (физ. минутка) СЛАЙДЫ 14,15
| - У. М. В любом музыкальном произведении указывается в каком темпе и с какой скоростью его нужно исполнять. Еще в 17 веке существовал прибор, позволяющий с абсолютной точностью исполнять произведение в заданном темпе. Прибор МЕТРОНОМ (греч. «метрос» - мера, «номос» - закон). - Задание «Прохлопай ритм» 1 ряд – целая нота 2 ряд – половинная нота 3 ряд – четвертная нота 4 ряд – восьмая нота |
| Слушаем музыку ритма СЛАЙДЫ 16,17
| - У. М. Перед вами ещё один портрет человека, которого я, не задумываясь, могу поставить в один ряд с Пифагором и Эйнштейном. Это тоже великий человек нашей планеты. Георгий Васильевич Свиридов, наш современник, композитор и пианист, Герой Социалистического труда. Ну, а раз появился портрет композитора, то обязательно в нашем классе зазвучит её величество музыка. Произведение, которое прозвучит, называется «Время, вперёд!». Оно написано к одноимённому кинофильму. Послушайте и постарайтесь представить, что рисует эта музыка, о чём она, какое воздействие оказывает на слушателя. (Учащиеся слушают музыку Свиридова «Время вперёд!»). Д: Как-будто ракета взлетает, появляется гордость за нашу Родину, новые свершения, движение вперёд, и т.д. У: С помощью каких средств музыкальной выразительности композитору удалось этого добиться? Д: На фоне пульсирующего ритма сопровождения мелодия в исполнении труб призывно взлетает всё выше и выше. У: В каком размере написал Георгий Свиридов своё произведение? (напеваем, дирижируем, обращаем внимание на сильные доли, определяем размер). У: Ребята, как вы думаете, об этом произведении лучше сказать, что оно мелодичное или ритмичное? Д: Ритмичное. У: А ритм состоит из чего? Д: Из длительностей. |
| Делим на такты СЛАЙД 18 | - У. М. Разделим ритмический рисунок на такты (сумма дробей в такте должна быть одинаковая!) ЗАДАНИЕ № 5 на слайде и бланках. |
| Диезы и бемоли СЛАЙД 19 | -У. Нотные записи звуков могут повышаться или понижаться. Для этого используются ЗНАКИ АЛЬТЕРАЦИИ (лат. слово «изменять» ). # Диез повышает на половину b Бемоль понижает на половину Соединим числа и знаки альтерации, вот что получим: 4 # -3b +7 # = 4 + ½ - 3 + ½ + 7 + ½ = 9 ½ 4 # = 4 + ½ 7# = 7 + ½ 3b = 3 - ½ Ответ: 9 ½ . ЗАДАНИЕ №6 1 вариант 2 вариант 5b + 8 # - 6# 10b – 2# + 5b Ответы: 6 целых ½, 11 целых ½. |
| Д/з СЛАЙД | творческое задание: придумать математические выражения используя знаки альтерации, схему длительности. |
| Итог. Рефлексия СЛАЙД 20 | - Чему мы научились на уроке? Д: Изучили длительности, научились разделять мелодию на такты, опираясь на закон сложения обыкновенных дробей, изучили знаки альтерации. - Где мы сможем применить полученные знания? Д: Если захотим сочинить музыку, то сможем грамотно разделить её на такты; в музыкальной школе, когда будут затруднения в диктанте с расстановкой длительностей в такте – поможет математика и т.д. У: Какой вывод можно сделать по сегодняшнему уроку? (дети пытаются сформулировать) Д: Музыка и математика очень разные, но они нужны друг другу. У: В бланке ответов поставьте плюс удовлетворены ли вы уроком? | Доволен |
| | Не понравилось |
| | Безразлично |
|
|
| Заключение СЛАЙД 22 | У. М. Недавно нам посчастливилось побывать на сцене нашего РДК и поучаствовать в ежегодном концерте «Аленький цветочек».В заключении нашего урока давайте исполним фрагмент песни «Далеко ли, близко ли». У: Я думаю, наш разговор не закончен, предлагаю вам самим поискать ещё точки соприкосновения математики и музыки. Ваши находки станут темами наших следующих необычных музыкально-математических уроков. До свидания! Спасибо за урок! |
| Дополнительное задание СЛАЙД 24 | ЗАДАНИЕ №7 - Сколько прямых углов в слове «НОТЫ»?
|


















