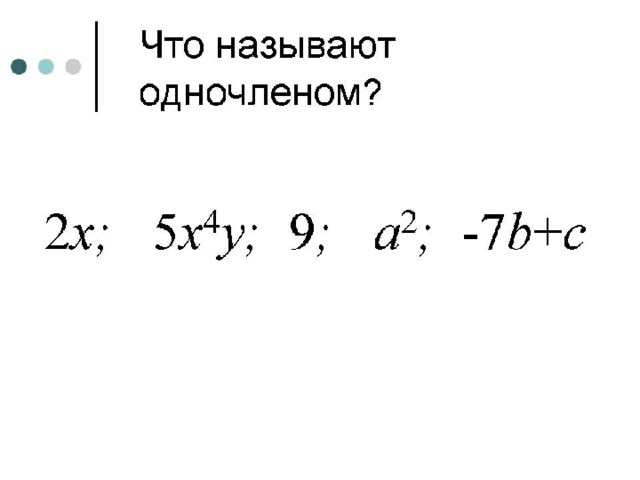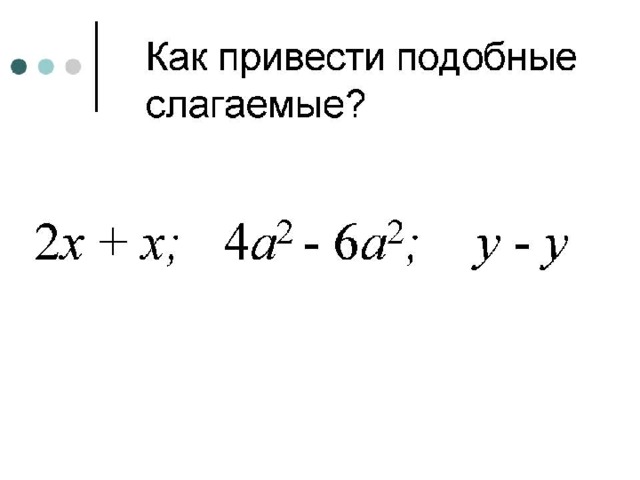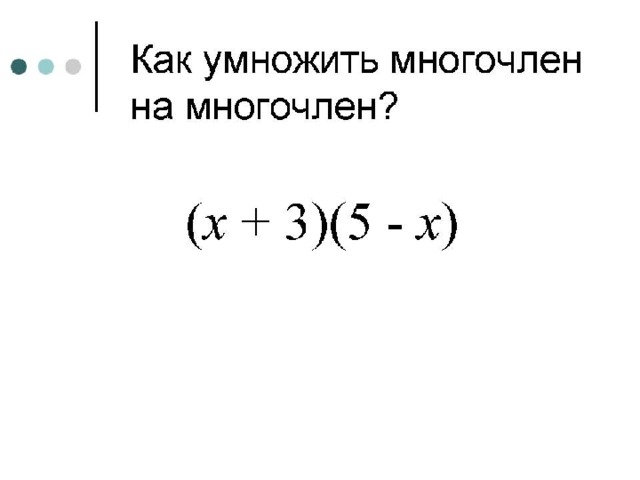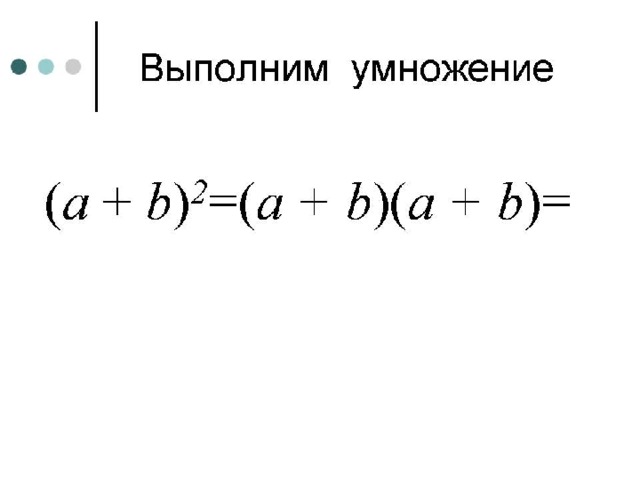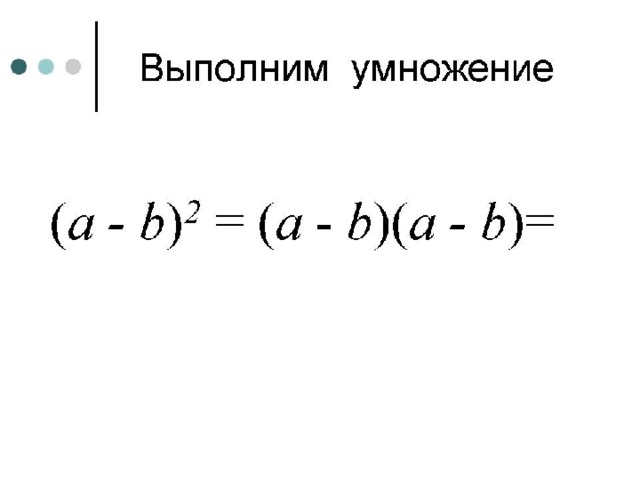Урок по алгебре в 7 классе
Тема урока:"Возведение в квадрат суммы и разности двух выражений"
Тип урока: формирование новых знаний.
Цели:
образовательная: вывести формулы квадратов суммы и разности двух чисел, сформировать умение учащихся практически применять эти формулы для упрощения выражений.
развивающая: развивать математическую речь, память, интерес к математике, умение логически рассуждать.
воспитательная: воспитывать активность, внимательность, самостоятельность.
Оборудование: Компьютер, телевизор, оформление классной доски для объяснения нового материала и закрепления знаний, карточки для самостоятельной работы.
Ход урока
Организационный момент.
- Здравствуйте ребята! На прошлых уроках мы научились умножать одночлены и многочлены. Сегодня мы начнём изучение новой темы “Формулы сокращенного умножения”. Эпиграфом нашему уроку послужат слова С. Ковалевской: “У математиков существует свой язык – это формулы”. На этом уроке мы познакомимся с возведением в квадрат суммы и разности двух выражений. Запишите, пожалуйста, тему нашего урока в тетрадь. Подумайте и скажите, какая у нас сегодня главная цель урока? (Вывести формулу квадратов суммы и разности двух чисел). Молодцы!
Повторение.
- Внимание на экран! Давайте вспомним:
Вопрос: Что называют одночленом?
Ответ: Произведение чисел, переменных и их степеней.
Действия с одночленами:
умножение одночленов 2х·3; 2·2х·3;
возведение в степень 32; (2х)2; верно ли 2х2=(2х)2
Вопрос: Что называют многочленом?
Ответ: Сумму одночленов.
Вопрос: Какие слагаемые называются подобными?
Ответ: Слагаемые с одинаковой буквенной частью.
Вопрос: Как привести подобные слагаемые?
Ответ: Сложить их числовые коэффициенты, а результат умножить на общую буквенную часть.
Вопрос: Как умножить одночлен на многочлен?
Ответ: Одночлен умножить на каждый член многочлена, а результат сложить.
Вопрос: Как умножить многочлен на многочлен?
Ответ: Алгоритм умножения многочлена на многочлен.
Изучение нового материала.
- При перемножении многочленов и приведении их к стандартному виду, а также при решении многих других задач очень полезными оказываются формулы сокращенного умножения.
Прежде всего, выведем формулы для возведения в квадрат суммы и разности двух выражений.
Выведем формулы (a + b)2 = a2+2ab+b2 и (a - b)2 = a2-2ab+b2
По алгоритму, который мы повторили в начале урока, перемножим эти многочлены (выполняют 2 учащихся у доски с объяснением каждого шага, при решении).
(a + b)(a + b) =a· (a + b) + b· (a + b) = a2+ab+ba+b2=a2+2ab+b2.
(a -b)(a - b) =a· (a –b) - b· (a – b) = a2-ab-ba+b2=a2-2ab+b2.
Итак, мы получили две формулы сокращенного умножения. Это формулы квадрата суммы и разности двух выражений. Запишем эти формулы и сформулируем их словесно.
(a + b)2 = a2+2ab+b2 (квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа).
(a - b)2 = a2-2ab+b2 (квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого числа на второе плюс квадрат второго числа).
Учим словесные формулировки и рассказываем соседу. После изучения – вслух.
Тождество (1) называют формулой квадрата суммы, тождество (2) – формулой квадрата разности. Эти формулы позволяют проще возводить в квадрат сумму или разность любых двух чисел (выражений). Они написаны на первом форзаце вашего учебника. И они нам понадобятся для разложения на множители многочленов даже в 11 классе.
Закрепление изученного.
- Рассмотрим примеры применения формулы квадрата суммы и квадрата разности.
На доске решаются задания
№ 799 (а, в, е, з)
а) (х + у)2 = х2 + 2ху + у2
в) (b + 3 )2 = b2 + 2· b· 3 + 32 = b2 + 6b + 9
е) (9 – у)2 = 92 - 2 ·9· у + у2 = 81 – 18у + у2
з) (15 – x)2 = 152 – 2 ·15· x + x2 = 225 – 30x + x2
№803 (а, в, ж)
а) (2x + 3)2 = (2x)2 + 2·2x ·3 + 32 = 4x2 + 12x + 9
в) (10 + 8k)2 = 102 + 2· 10· 8k + (8k)2 = 100 +160k + 16k2
ж) (0,3x – 0,5a)2 = (0,3x)2 – 2 ·0,3x ·0,5a + (0,5a)2 = 0,09x2 – 0,3xa + 0,25a2
Этап контроля и самоконтроля.
Каждому ученику приготовлены индивидуальные карточки, которые они подписывают. И выполняют самостоятельно задания. В конце урока сдают.
Пример карточки:
| Ф.И. учащегося: |
| а) (m+n)2= |
| б) (8-a)2= |
| в) (40+b)2= |
| г) (0,2a-x)2= |
Дополнительное задание для успешных учеников:
Прочитай решение задания и выполни по образцу
Выполните возведение в квадрат (2а + b4)2 = (2a)2 + 2· 2a ·b4 + (b4)2 = 4a2 + 4ab4 + b8
(4y3 – 0,5y2)2 = (4y3)2 – 2·4y3·0,5y2 + (0,5y2)2 = 16y6 – 4y5 + 0,25y4
(3x + c2)2 = (5a5 – 0,2a2)2 =
Задание на дом.
П. 32. стр.153 – 154, выучить формулы квадрата суммы и разности двух выражений, выполнить № 800 (а, в,д,ж), № 803 (б,д,з) повторение №831
7. Подведение итогов урока. Рефлексия.
- Ребята, с какими формулами сокращенного умножения мы с Вами сегодня познакомились. Сформулируйте словами. Для чего нужны формулы? (Для упрощения выражений).
- Оценки за урок.
- Спасибо за урок.
8. Дополнительно: геометрическое доказательство формул (стр. 164, 166)