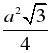Урок №
ТЕОРЕМА ПИФАГОРА
Цели: продолжить рассматривать решение задач с помощью теоремы Пифагора и проверить навыки решения задач по этой теме.
Ход урока
I. Проверка домашнего задания.
1. Заслушать сообщения о других доказательствах теоремы Пифагора.
2. Ответить на возможные вопросы по домашнему заданию.
II. Решение задач.
№ 517 (разобрать решение без записи в тетрадь).
Решение
1) Рассмотрим АВС. Сторона ВС – наибольшая. Проверим, не выполняется ли в нем условие
ВС2 = АВ2 + АС2
132 = 122 + 52
169 = 144 + 25
169 = 169.
АВС – прямоугольный по теореме, обратной теореме Пифагора.
2) Аналогично доказывается, что АDС – прямоугольный с прямым углом DСА.
3) SАВСD = SАВС + SDАС = АВ · АС + АС · DС = АС (АВ + DС) =
= · 12 (5 + 9) = 84 (см2).
№ 496.
Решение
1) Пусть АD = ВС = х.
Тогда ВD = 3 – х.
2) По теореме Пифагора для треугольника ВСD
х2 = (3 – х)2 + ;
х2 = 9 – 6х + х2 + 3;
6х = 12;
х = 2;
ВС = 2 см.
3) По теореме Пифагора для треугольника АСD.
AC = (см).
№ 497 (без записи в тетрадь).
Решение
АВD – прямоугольный.
По теореме Пифагора
АВ2 = BD2 + AD2,
BD =,
BD =,
AD + AB – полупериметр.
AD + AB = 25 (см).
ВD = = 5 (см).
№ 489.
1) ВD – высота АВС, которая является и медианой.
АD = DС = .
2) АВD – прямоугольный по теореме Пифагора.
ВD =
SDАВС = ВD · АС = · · a =.
III. Самостоятельная работа.
Вариант I
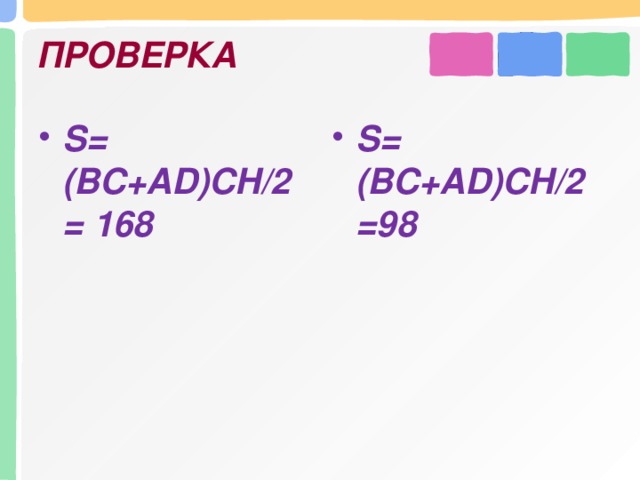
В прямоугольной трапеции основания равны 22 см и 6 см, большая боковая сторона – 20 см. Найдите площадь трапеции.
Вариант II
В прямоугольной трапеции боковые стороны равны 7 см и 25 см, а меньшее основание равно 2 см. Найдите площадь трапеции.
Вариант III
(для более подготовленных учащихся)
Диагональ АС прямоугольной трапеции АВСD перпендикулярна боковой стороне СD и составляет угол 60° с основанием АD. Найдите площадь трапеции, если АD = 24 см.
IV. Итоги урока.
Площадь равностороннего треугольника S =, где а – сторона треугольника.
Домашнее задание: № 518; №515
№499
)
Для желающих.
Рассмотреть самостоятельно решение № 524 (вывод формулы Герона).
Просмотр содержимого документа
«КОНСПЕКТ УРОКА»
Урок 11
ТЕОРЕМА ПИФАГОРА
Цели: продолжить рассматривать решение задач с помощью теоремы Пифагора и проверить навыки решения задач по этой теме.
Ход урока
I. Проверка домашнего задания.
1. Заслушать сообщения о других доказательствах теоремы Пифагора.
2. Ответить на возможные вопросы по домашнему заданию.
II. Решение задач.
№ 517 (разобрать решение без записи в тетрадь).
Решение
| 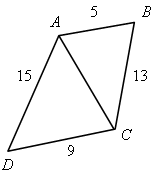
| 1) Рассмотрим  АВС. Сторона ВС – наибольшая. Проверим, не выполняется ли в нем условие АВС. Сторона ВС – наибольшая. Проверим, не выполняется ли в нем условие ВС2 = АВ2 + АС2 132 = 122 + 52 169 = 144 + 25 169 = 169.  АВС – прямоугольный по теореме, обратной теореме Пифагора. АВС – прямоугольный по теореме, обратной теореме Пифагора.
|
2) Аналогично доказывается, что  АDС – прямоугольный с прямым углом DСА.
АDС – прямоугольный с прямым углом DСА.
3) SАВСD = SАВС + SDАС = 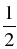 АВ · АС +
АВ · АС + 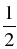 АС · DС =
АС · DС = 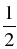 АС (АВ + DС) =
АС (АВ + DС) =
= 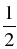 · 12 (5 + 9) = 84 (см2).
· 12 (5 + 9) = 84 (см2).
№ 496.
Решение
1) Пусть АD = ВС = х.
Тогда ВD = 3 – х.
| 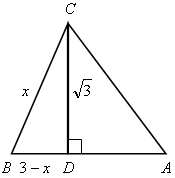
| 2) По теореме Пифагора для треугольника ВСD х2 = (3 – х)2 + 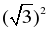 ; ; х2 = 9 – 6х + х2 + 3; 6х = 12; х = 2; ВС = 2 см. |
3) По теореме Пифагора для треугольника АСD.
AC = 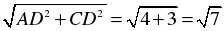 (см).
(см).
№ 497 (без записи в тетрадь).
Решение
| 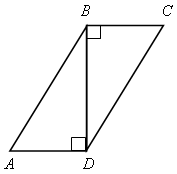
|  АВD – прямоугольный. АВD – прямоугольный. По теореме Пифагора АВ2 = BD2 + AD2, BD = 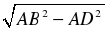 , , BD = 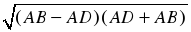 , , AD + AB – полупериметр. AD + AB = 25 (см). |
ВD = 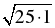 = 5 (см).
= 5 (см).
№ 489.
| 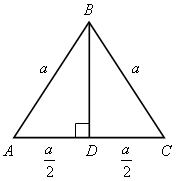
| 1) ВD – высота  АВС, которая является и медианой. АВС, которая является и медианой. АD = DС = 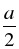 . . 2)  АВD – прямоугольный по теореме Пифагора. АВD – прямоугольный по теореме Пифагора. ВD =  |
SАВС = 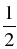 ВD · АС =
ВD · АС = 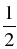 ·
·  · a =
· a = 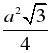 .
.
III. Самостоятельная работа.
Вариант I
В прямоугольной трапеции основания равны 22 см и 6 см, большая боковая сторона – 20 см. Найдите площадь трапеции.
Вариант II
В прямоугольной трапеции боковые стороны равны 7 см и 25 см, а меньшее основание равно 2 см. Найдите площадь трапеции.
Вариант III
(для более подготовленных учащихся)
Диагональ АС прямоугольной трапеции АВСD перпендикулярна боковой стороне СD и составляет угол 60° с основанием АD. Найдите площадь трапеции, если АD = 24 см.
IV. Итоги урока.
Площадь равностороннего треугольника S = 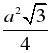 , где а – сторона треугольника.
, где а – сторона треугольника.
Домашнее задание: № 518; №515
№499
)
Для желающих.
Рассмотреть самостоятельно решение № 524 (вывод формулы Герона).
Просмотр содержимого презентации
«презентация по геометрии 8кл»