| Четверть: II Урок: 18 Раздел: 9.2A Квадратные уравнения.
| 
НИШ ХБН г. Атырау |
| Дата: 17.11.16 | ФИО учителя: Ибрашева Т.М. |
| Класс: 9C | Количество присутствующих: 17 | отсутствующих: |
| Тема урока: | Решение квадратных уравнений. Урок обобщения |
| Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу) | Учащиеся будут: АУ 9.1 знать вид квадратного уравнения 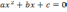 где 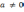 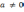 ; ; АУ 9.2 знать, что если b или с равно 0, то квадратное уравнение ax2 + bx + c = 0 не полное. АУ 9.3 использовать дискриминант для определения количества действительных корней квадратного уравнения; АУ 9.4 решать квадратные уравнения и уравнения, приводящиеся к ним, такие, как: 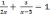 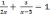 ; ; АУ 9.5 знать и применять формулы Виета, связанные с суммой и произведением корней квадратного уравнения. |
| Цели урока: | Повторить и обобщить знания уч-ся: – по видам квадратного уравнения; – по использованию дискриминант для определения количества действительных корней квадратного уравнения; – по решению квадратных уравнений и уравнений, приводящихся к ним, такие, как: 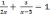 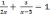 ; ; – по знанию и применению формулы Виета, связанные с суммой и произведением корней квадратного уравнения; – по развитию навыков самообучения через задания для критического мышления. |
| Критерии успеха: | Учащиеся: – знают вид квадратного уравнения; – умеют использовать дискриминант для определения количества действительных корней квадратного уравнения; – умеют решать квадратные уравнения и уравнения, приводящиеся к ним, такие, как: 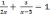 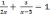 ; ; – знают и применяют формулы Виета, связанные с суммой и произведением корней квадратного уравнения; – владеют навыками самообучения. |
| Языковые цели:
| Учащиеся смогут: Понимать определение квадратного уравнения и знать некоторые из его применений в реальной жизни устно и/или письменно Лексика и терминология, специфичная для предмета: Квадратное уравнение Наивысшая степень переменной (первый/второй/ средний/последний) член, (степень) переменной Целое число, коэффициент, показатель степени, удалить/раскрыть скобки, наибольший общий делитель, упростить, решить Полезные выражения для диалогов и письма: Квадратное уравнение – это уравнение, в котором … самой большой степенью переменной является квадрат Понимание квадратных уравнений помогло человечеству понять: как рассчитать скорость движущих объектов как рассчитать тормозной путь машины как сконструировать спутниковую тарелку как проектировать здания как планеты движутся вокруг солнца как летают самолеты как футбольный мяч движется по воздуху как работает маятник как движется пуля |
| Школьные ценности:
| Уважение по отношению к себе и окружающим: уважение к родному языку, так и к другим языкам – воспитывается при работе с терминами урока, при решении прикладных задач. Сотрудничество: формирование навыков сотрудничества и развитие конструктивного подхода – осуществляется через работу в группе, паре. Академическая честность: уважение идей и мыслей других людей – воспитывается при работе с разными источниками информации. Обучение на протяжении всей жизни: развитие таких умений и навыков, которые будут способствовать самостоятельному обучению учащихся – формируются при индивидуальной работе. |
| Взаимосвязь с «Мәңгілік ел»: | Общество всеобщего труда: учащиеся моделируют и решают задачи практической направленности, связанные с расчетами по определению затрат труда |
| Межпредметные связи: | Прикладная математика, физика. |
| Навыки использования ИКТ: | Развитие навыков работы в Power Point, с ИД. |
| Предварительные знания:
| Понимание квадратных корней, умение преобразовывать выражения; навыки умножения и деления. Понимание выражений, равенств и неравенств; понимание, как уравнение может быть представлено графически; определение делителей чисел. |
| Тип урока: | Урок обобщения и систематизации знаний. |
| Ход урока: |
| Запланированные этапы урока | Запланированная деятельность на уроке | Ресурсы |
| Начало урока 5 мин | 1.Орг. момент Приветствие. Каждый ученик выбирает листок с уравнением и дает краткую характеристику о нём. По виду уравнения класс делится на 4 группы. Прежде, чем сесть на место, выходят к доске заполняют детонантный граф. Совместно с учащимися формулируется тема урока, цель. | Рабочая программа 9 класс; Рабочий план 9 класс; Учебная литература: 1) Алгебра 8. Шыныбеков А.Н. Учебник для 8 класса общеобразовательной школы. 3-е изд. – Алматы: Атамұра, 2012. – 288 с. ISBN 978-601-282-527-5 Глава 2. п.1 стр. 61-63
2) Алгебра. 8 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. – 10-е изд., испр. - М. : Мнемозина, 2010. - 384 с.: ил. Глава 4. п.9 стр.174-176 3) Алгебра. 8 класс : учеб. для учащихся общеобразоват. учреждений / А.Г. Мордкович. – 14-е изд., испр. - М. : Мнемозина, 2012. - 215 с.: ил. Глава 4. п.24 стр.174-176 |
| Середина урока 33 мин | Актуализация опорных знаний. Стадия вызова Работа со всем классом. Тест на ИД с помощью программы Plickers. 1. Формула дискриминанта: а) D=b2 – 4a b) D=b2 + 4ac c) D=b2 – 4ac 2. Если D = 0, то назовите формулу и сколько корней у уравнения: а) x = – b/2a, один корень b) x = b/2a, нет корней c) x = – b/2, два разных корня 3. Если D а) один корень b) нет корней c) два корня 4. Если D 0, то назовите формулу и сколько корней у уравнения: а) x = – b/2a, один корень b) нет корней c) 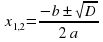 , два корня , два корня 5. Формула теоремы Виета для неприведенного уравнения: а) x1 + x2 = – b/a и x1 x2 = c/a x2 = c/a b) x1 + x2 = – b и x1 x2 = c x2 = c c) x1 + x2 = b/a и x1 x2 = – c/a x2 = – c/a Ответы: 1. c 2. a 3. b 4. c 5. a Закрепление знаний. Работа в группе. Решение КВУР различными методами: 1) с использованием формулы корней: (2х + 3)2 – (х – 1)2 = – 8; Ответ: – 2; 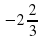 Оценивание по критериям. | Навыки | Критерии успеха | Итог | | Критическое мышление. Анализ | Анализирует условие уравнения на выбор применения ФСУ |
| | Применение знаний | Верно использует формулы корней при решении квадратного уравнения | – 2; 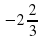
| | Оценка | Обосновывает свое решение |
| 2) по теореме Виета: Разность квадратов корней приведенного квадратного уравнения равна 24. Второй коэффициент этого уравнения равен 2. Найдите свободный член уравнения. Ответ: – 35 Оценивание по критериям. | Навыки | Критерии успеха | Итог | | Критическое мышление. | Интепретирует условие задачи для составления уравнения с применением теоремы Виета |
| | Применение знаний | Умеет применять теорему Виета при решении квадратного уравнения | – 35 | | Оценка | Обосновывает свое решение |
|
3) с применением ФСУ, выделение квадрата двучлена: 4х2 – 4х – 3=0; Ответ: – 0,5; 1,5 Оценивание по критериям. | Навыки | Критерии успеха | Итог | | Оценка | Оценивает какую ФСУ применить в конкретном примере |
| | Применение знаний | Умеет решать квадратное уравнение с применением ФСУ | – 0,5; 1,5 | | Рефлексия | Обосновывает свое решение |
|
4) методом разложения на множители: 2х2 – 5х + 2 = 0; Ответ: 0,5; 2 Оценивание по критериям. | Навыки | Критерии успеха | Итог | | Критическое мышление. Анализ | Анализирует условие уравнения для выбора слагаемых для группировки |
| | Применение знаний | Умеет решать методом разложения на множители | 0,5; 2 | | Оценка | Обосновывает свое решение |
|
5) метод введения новой переменной: 3(x2 + 2x)2 = 35(x + 1)2 + 115 Ответ: – 5; 3 Оценивание по критериям. | Навыки | Критерии успеха | Итог | | Критическое мышление. Анализ | Анализирует условие уравнения на выбор выражения для замены |
| | Применение знаний | Умеет решать методом введения новой переменной | – 5; 3
| | Оценка | Обосновывает свое решение |
|
Решение квадратных уравнений графическим способом. Работа в паре. 1) х2 – х– 2=0; 2) х2+1,5х–2,5=0; 3)х2=0,5х+3; 4) 7х= – х2; 5)4+9х2=0 ; 6) 4х2=– 4х– 1 ; 7) 3х2=4х+7; 8) 2х= х2+1; 9) 0,5х2=6.
Оценивание по критериям. | Навыки | Критерии успеха | Итог | | Критическое мышление. Анализ | Разделяет на функции
|
| | Применение знаний | Правильно строит графики функций Находит на графике решение уравнений |
| | Оценка | Обосновывает свое решение |
|
Дополнительно. Индивидуальная работа. Мяч брошен вертикально ввверх с начальной скоростью 40м/с. Через сколько секунд он окажется на высоте 60м? Решение: 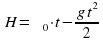
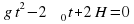
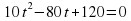
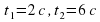 Через 2с – при подъеме окажется на высоте 60м Через 2с – при подъеме окажется на высоте 60м
Через 6c после прохождения верхней точки при движении вниз окажется на высоте 60м
Оценивание по критериям. | Навыки | Критерии успеха | Итог | | Критическое мышление. Анализ | Анализирует условие уравнения на выбор переменной |
| | Применение знаний | Правильно составляет уравнение по условию задачи |
| | Решает уравнение и находит верный ответ |
| | Оценка | Обосновывает свое решение |
|
|
| Конец урока 2 мин | Домашнее задание. По учебнику Ю. Макарычева Алгебра 8 класс: № 689. Радиус одной из двух окружностей, имеющих общий центр, на 5см больше радиуса другой. Площадь кольца, заключенного между этими окружностями, составляет 1,25 площади малого круга. Найдите радиусы окружностей.
В конце урока рефлексия: Учащиеся заполняют таблицу с помощью стикеров: | № | Ф.И. уч-ся | Умеют решать КВУР различными методами | | По формуле корней | По теореме Виета | С применением ФСУ | Разложением на множители | Через введение новой переменной | Графический метод | Прикладные задачи | | 1 |
|
|
|
|
|
|
|
|
|
| Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися? | Оценивание – как Вы планируете проверить уровень усвоения материала учащимися? | Здоровье и соблюдение техники безопасности |
|
|
|
|
| Рефлексия по уроку Были ли цели урока/цели обучения реалистичными? Все ли учащиеся достигли ЦО? Если нет, то почему? Правильно ли проведена дифференциация на уроке? Выдержаны ли были временные этапы урока? Какие отступления были от плана урока и почему? | Используйте данный раздел для размышлений об уроке. Ответьте на самые важные вопросы о Вашем уроке из левой колонки. |
|
|
| Общая оценка Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)? 1: 2: Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)? 1: 2: Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках?
|

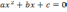
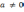
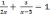
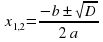 , два корня
, два корня x2 = c/a
x2 = c/a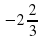
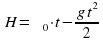
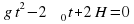
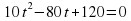
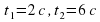 Через 2с – при подъеме окажется на высоте 60м
Через 2с – при подъеме окажется на высоте 60м















