Муниципальное общеобразовательное учреждение
Мамонтовская основная школа
Урок по теме
«Определение степени с натуральным показателем»
Цель: ввести понятие степени с натуральным показателем.
Задачи:
- Образовательная: научить ребят работать с определением степени числа с натуральным показателем на примерах некоторых заданий.
- Развивающая: учить детей приёмам мыслительной деятельности, опираясь на их субъектный опыт, мотивируя каждый шаг учебной деятельности, развивать кругозор, углубить материал по данной теме.
- Воспитательная: воспитывать стремление детей к получению новых знаний, чувства товарищества, формировать объективную самооценку знаний.
Оборудование: компьютер, мультимедийный проектор, интерактивная доска,,рабочие тетради
Ход урока
1. Орг. момент
Приветствие детей, объявление темы и цели урока, запись в тетрадь числа и темы урока (слайд 1), оформление тетрадей с печатной основой (ТПО).
2. Актуализация опорных знаний
- Вспомним определение функции (слайд 2).
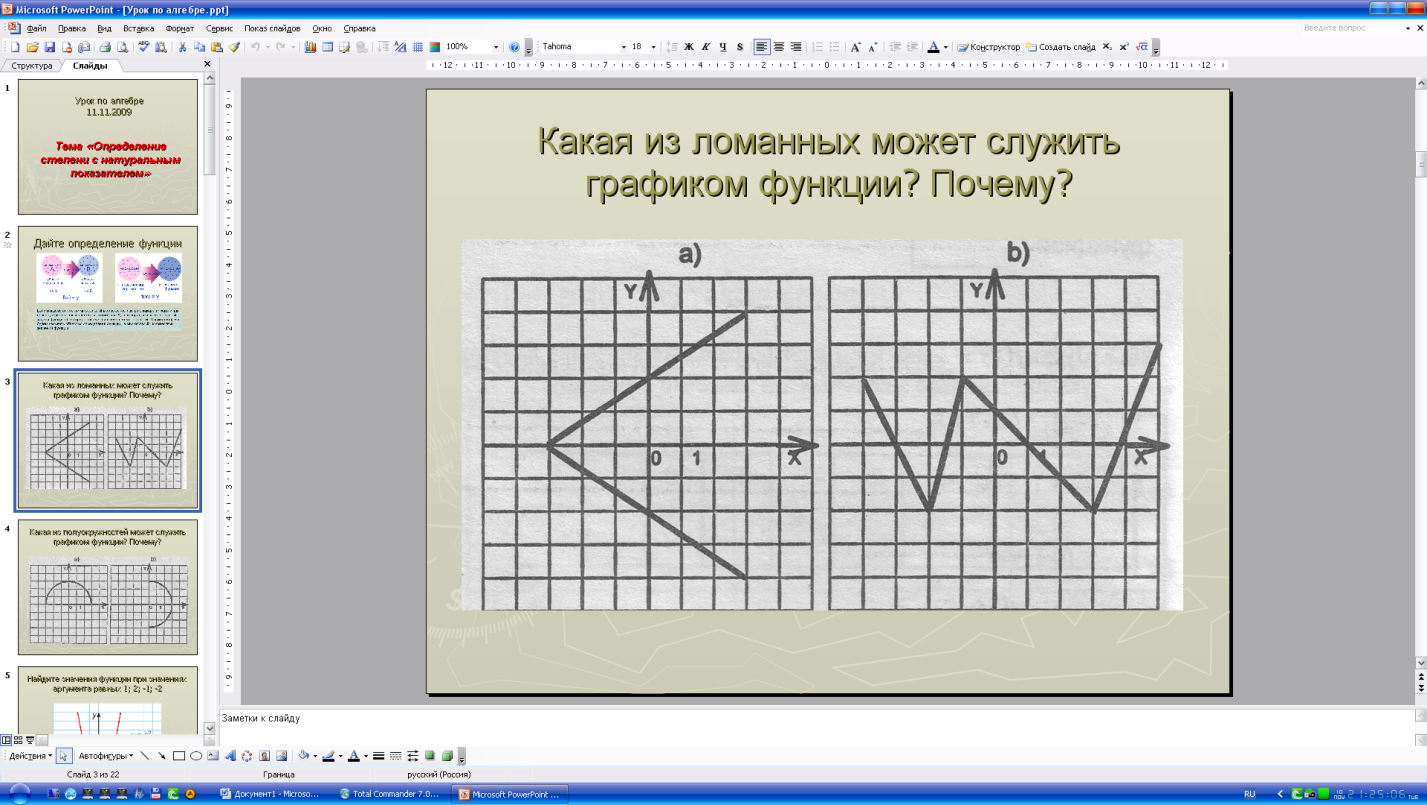
- Какая из ломаных может служить графиком функции? Почему?
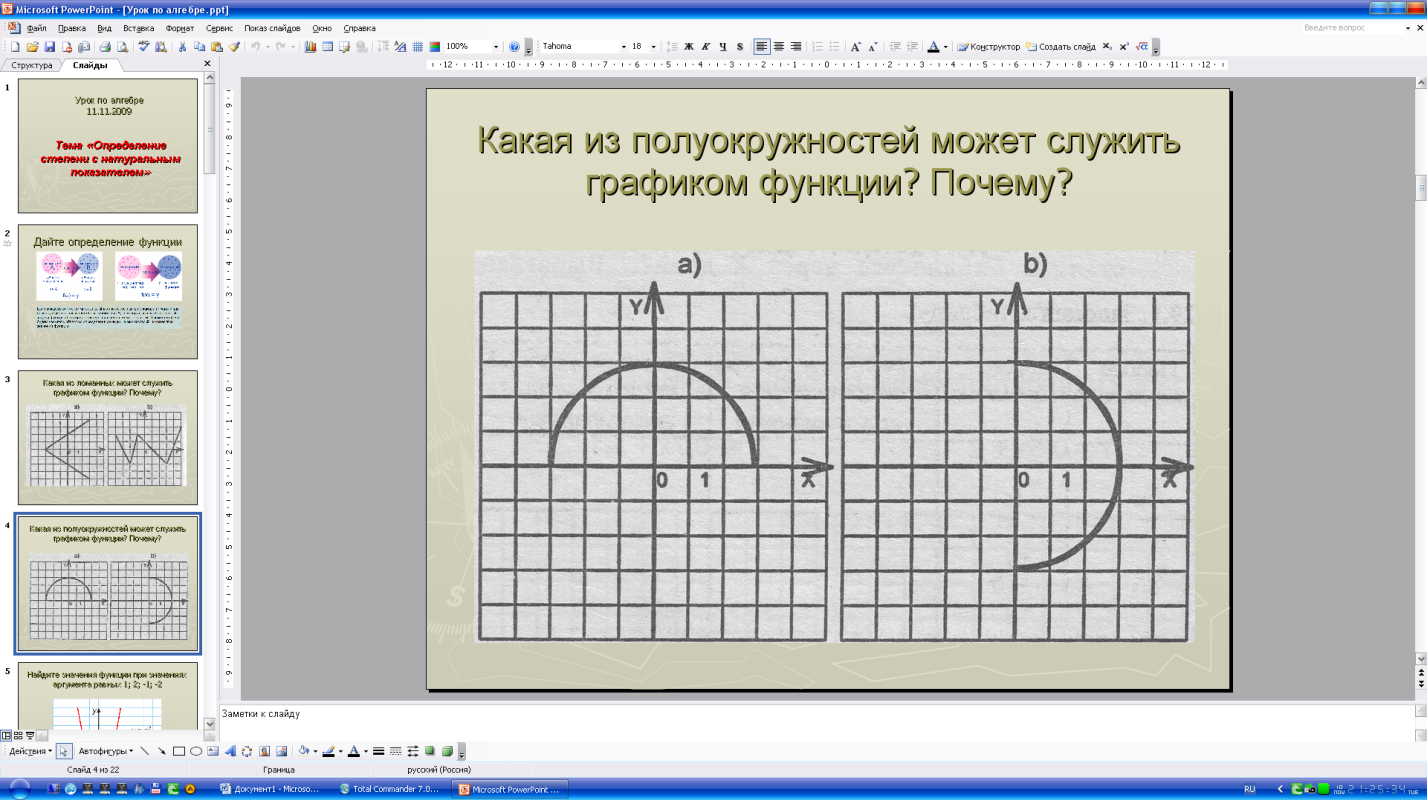
- Какая из полуокружностей может служить графиком функции? Почему?
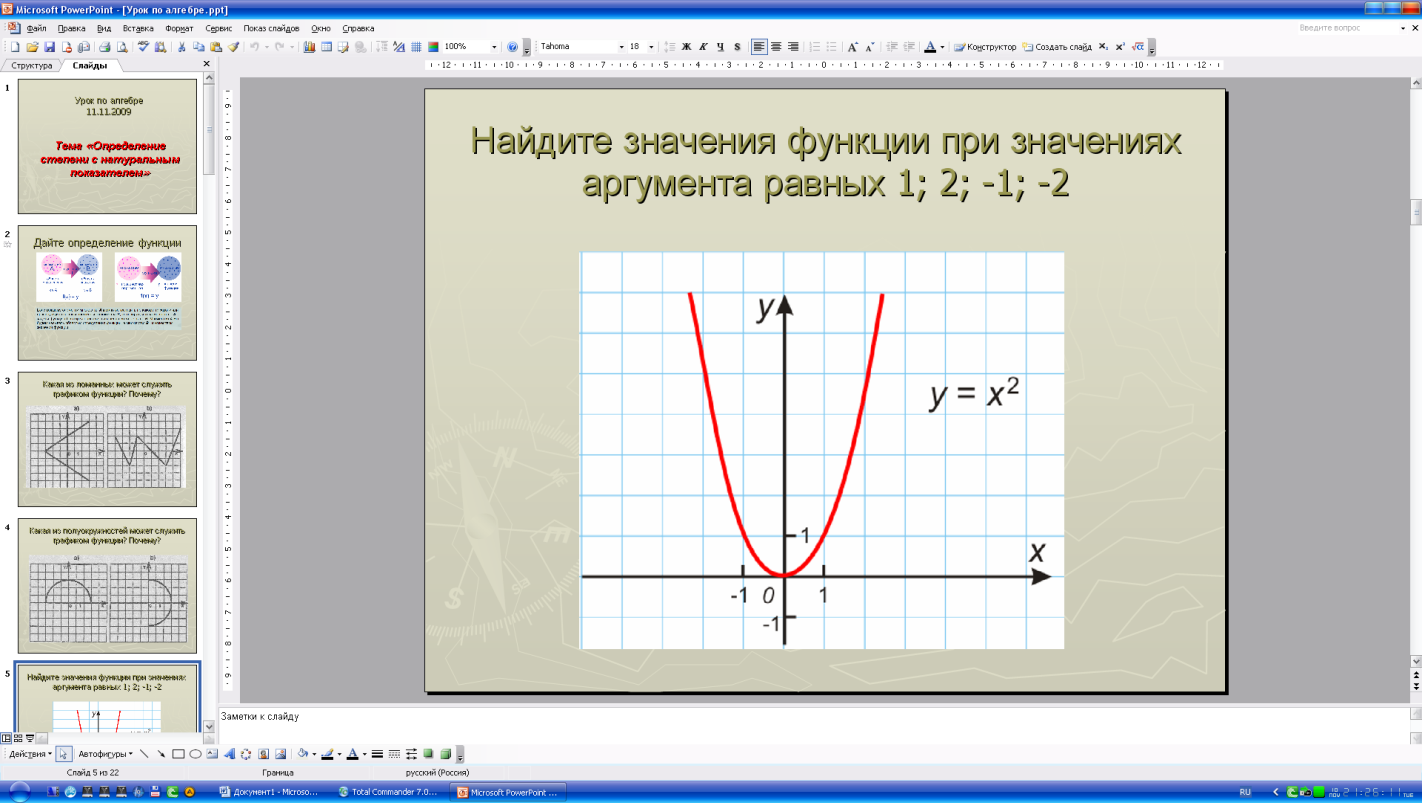
- Перед вами график функции у=х2
По графику найдите значение функции при следующих значениях аргумента: -2, -1, 1, 2.
График этой функции называется параболой, мы будем его скоро изучать.
Возрастающей или убывающей является эта функция?
- Найти значение выражения:
32; 23; 31; 42; 0,82; 02; 0,13; 13
- Что значит возвести число в квадрат, в куб?
- Упростите выражение
x·x
a·a·a
y·a·c·c·y·a·y·y·a
2·2·2·2·2
2+2+2+2+2
Чем отличаются 2 последних выражения?
3. Объяснение нового материала
- Сегодня мы попробуем дать определение степени с натуральным показателем. Для этого вспомним, как найти объем куба. (слайд 9)
Перед вами куб, у которого все измерения равны 3, как найти его объем? (V=3?3?3)
- А теперь поставим три кубика, найдите их общий объем (V=3?3?3?3=34) – читаем «три в четвертой степени».
- А как найти это число? (запись в тетрадь)
- Как можно по-другому записать an? (an=a?a?a?…?a). Дайте определение степени с натуральным показателем. (дети формулируют правила)
- Проверьте себя.
- Прочитайте правило на слайде. А теперь найдите это правило в учебнике и прочитайте еще раз.
- заполняем таблицу «Определения. Обозначения.» и комментируем по ходу заполнения.
4. Закрепление изученного материала
- Заполним таблицу письменно, ученики выходят по очереди к интерактивной доске (первый заполняет столбики 1, 3, 5, второй – столбики 2, 4, 6.
Степень
(-9)42
53
(3xy)3
(x+y)5
2n-1
(a-b)n
Основание степени
Показатель степени
- Продолжаем работу, ученики по одному выходят к доске на следующие задания.
- Запишите произведение в виде степени
0,9·0,9·0,9
(-6)·(-6)·(-6)·(-6)
ССССССС
(-x)·(-x)·(-x)·(-x)·(-x)
(a-b)(a-b)
(xy)(xy)(xy)(xy)(xy)
2·2·2·a·a·b·b·b·b
a2·a3·a
- Представьте степень в виде произведения
3,54
(-0,1)3
(-100)4
(-a)6
- Вспомним материал 5 класса. Часто при решении примеров требуется знать степени чисел 2 и 3. Заполним таблицу в ТПО и на интерактивной доске (слайд 17).
n
1
2
3
4
5
6
7
8
9
10
2n
3n
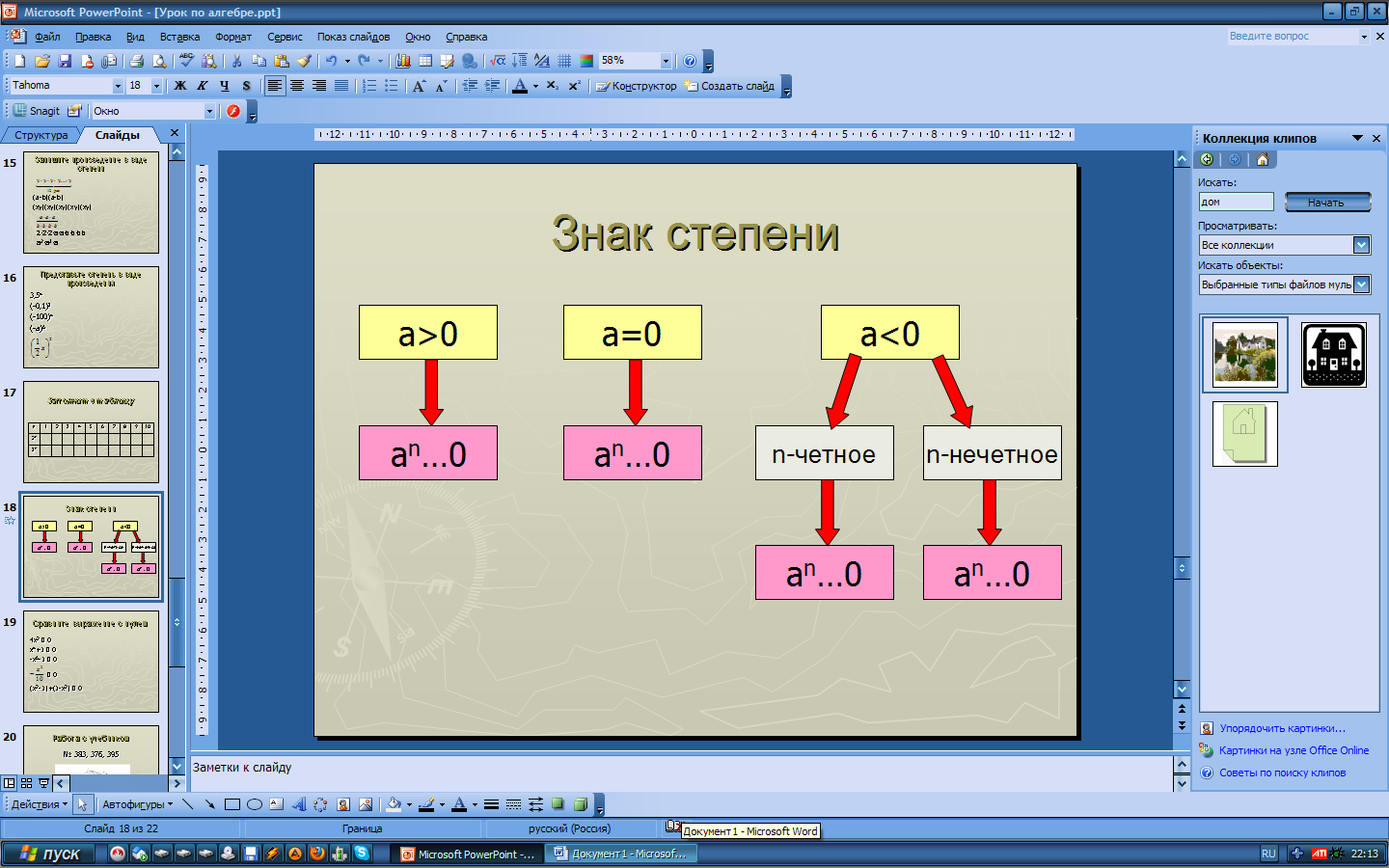
- Перед тем, как выполнять задания на нахождение значений степени заполним таблицу «Знак степени». Учитель у доски, фронтальный опрос
- Сравните выражение с нулем (слайд 19), один человек у доски, остальные работают в ТПО.
4x2 0
x4+1 0
-x6-1 0
0
(x2-1)+(1-x2) 0
- Работаем с учебником выполняем номера 383, 376, 395.
5. Итог урока
- Что называется степенью числа a с натуральным показателем n?
- Найдите ошибки в примерах:
3·3·3·3·3 = 53
(-2)2= -2·2= -4
81 = 1
113 = 13
6. Домашнее задание
П.18
№ 377, 382, 385
Муниципальное общеобразовательное учреждение
Мамонтовская основная школа
Урок по теме
«Определение степени с натуральным показателем»
Цель: ввести понятие степени с натуральным показателем.
Задачи:
- Образовательная: научить ребят работать с определением степени числа с натуральным показателем на примерах некоторых заданий.
- Развивающая: учить детей приёмам мыслительной деятельности, опираясь на их субъектный опыт, мотивируя каждый шаг учебной деятельности, развивать кругозор, углубить материал по данной теме.
- Воспитательная: воспитывать стремление детей к получению новых знаний, чувства товарищества, формировать объективную самооценку знаний.
Оборудование: компьютер, мультимедийный проектор, интерактивная доска,,рабочие тетради
Ход урока
1. Орг. момент
Приветствие детей, объявление темы и цели урока, запись в тетрадь числа и темы урока (слайд 1), оформление тетрадей с печатной основой (ТПО).
2. Актуализация опорных знаний
- Вспомним определение функции (слайд 2).
- Какая из ломаных может служить графиком функции? Почему?
- Какая из полуокружностей может служить графиком функции? Почему?
- Перед вами график функции у=х2
По графику найдите значение функции при следующих значениях аргумента: -2, -1, 1, 2.
График этой функции называется параболой, мы будем его скоро изучать.
Возрастающей или убывающей является эта функция?
- Найти значение выражения:
32; 23; 31; 42; 0,82; 02; 0,13; 13
- Что значит возвести число в квадрат, в куб?
- Упростите выражение
x·x
a·a·a
y·a·c·c·y·a·y·y·a
2·2·2·2·2
2+2+2+2+2
Чем отличаются 2 последних выражения?
3. Объяснение нового материала
- Сегодня мы попробуем дать определение степени с натуральным показателем. Для этого вспомним, как найти объем куба. (слайд 9)
Перед вами куб, у которого все измерения равны 3, как найти его объем? (V=3?3?3)
- А теперь поставим три кубика, найдите их общий объем (V=3?3?3?3=34) – читаем «три в четвертой степени».
- А как найти это число? (запись в тетрадь)
- Как можно по-другому записать an? (an=a?a?a?…?a). Дайте определение степени с натуральным показателем. (дети формулируют правила)
- Проверьте себя.
- Прочитайте правило на слайде. А теперь найдите это правило в учебнике и прочитайте еще раз.
- заполняем таблицу «Определения. Обозначения.» и комментируем по ходу заполнения.
4. Закрепление изученного материала
- Заполним таблицу письменно, ученики выходят по очереди к интерактивной доске (первый заполняет столбики 1, 3, 5, второй – столбики 2, 4, 6.
Степень
(-9)42
53
(3xy)3
(x+y)5
2n-1
(a-b)n
Основание степени
Показатель степени
- Продолжаем работу, ученики по одному выходят к доске на следующие задания.
- Запишите произведение в виде степени
0,9·0,9·0,9
(-6)·(-6)·(-6)·(-6)
ССССССС
(-x)·(-x)·(-x)·(-x)·(-x)
(a-b)(a-b)
(xy)(xy)(xy)(xy)(xy)
2·2·2·a·a·b·b·b·b
a2·a3·a
- Представьте степень в виде произведения
3,54
(-0,1)3
(-100)4
(-a)6
- Вспомним материал 5 класса. Часто при решении примеров требуется знать степени чисел 2 и 3. Заполним таблицу в ТПО и на интерактивной доске (слайд 17).
n
1
2
3
4
5
6
7
8
9
10
2n
3n
- Перед тем, как выполнять задания на нахождение значений степени заполним таблицу «Знак степени». Учитель у доски, фронтальный опрос
- Сравните выражение с нулем (слайд 19), один человек у доски, остальные работают в ТПО.
4x2 0
x4+1 0
-x6-1 0
0
(x2-1)+(1-x2) 0
- Работаем с учебником выполняем номера 383, 376, 395.
5. Итог урока
- Что называется степенью числа a с натуральным показателем n?
- Найдите ошибки в примерах:
3·3·3·3·3 = 53
(-2)2= -2·2= -4
81 = 1
113 = 13
6. Домашнее задание
П.18
№ 377, 382, 385


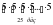

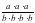
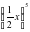
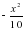 0
0















