Урок по теме "Координатная плоскость"

В ходе данного урока ребята убедятся в то, что полученные знания могут применяться не только в математике. Это поможет формированию у них целостного восприятия мира. Урок способствует расширению кругозора, развитию логического и абстрактного мышления, наблюдательности детей.

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«Координатная плоскость»

МБОУ «Сидоровская средняя общеобразовательная школа»

МБОУ «Тамбовская средняя общеобразовательная школа»

Урок по теме

«Координатная плоскость»

Учителя:

Ященко Мария Андреевна – учитель физики и математики

Герман Лидия Андреевна - учитель математики

«Координатная плоскость»

Тип урока: обобщения и систематизации знаний.

Цели урока:

закрепить навыки определения координаты точки в координатной плоскости и построения точки по ее координатам;
обобщить и систематизировать материал по теме «Координатная плоскость»; установить связи между теорией и практикой;
развивать у учащихся умение применять логические операции – сравнение; анализ; развивать и активизировать познавательные процессы – мышление, внимание, восприятие; приобщение учащихся к информационным технологиям;
воспитание интереса к математике и ее приложениям.

Задачи урока:

научить отмечать точки на координатной плоскости;
развивать мышление, самостоятельность;
воспитывать аккуратность, доброжелательное отношение друг к другу.

Необходимое оборудование и материалы:

Компьютер, проектор, экран
Презентация к уроку.

Данное занятие следует проводить в конце изучения темы.

Ход урока.

Здравствуйте ребята! Садитесь.
Сегодня у нас итоговый урок по теме: «Координатная плоскость». Выполняя различные задания, вы покажете нам свои знания, умения и навыки, способность применять их в различных ситуациях.
(слайд 2) А фраза - «Жить на плоскости не скучно, веселей, чем на прямой…» - будет эпиграфом нашего урока.

Включаю настольную лампу.

Позади трудный день …

Казалось, он не закончится …

Очень устала.

(изменив интонацию)

А сегодня всё совсем по-другому …

Солнечные лучи кажутся ярче,

Листва шуршит под ногами совсем не так как вчера

И какое-то ощущение лёгкости.

Беседа с учащимися:

А от чего зависит наше настроение? (после рассуждений сделать вывод о том, что у человека хорошее настроение, если он здоров, счастлив, успешен и всё это происходит одновременно, то есть в системе)

Учитель записывает на доску слово «система».

А какой смысл вы вкладываете в это слово? (ответы детей)
Какое известное вам слово спрятано в слове «система»? (слово «тема»)
Что оно означает?

Рассказ учителя: «Тема» - нечто заданное, «сис» - составленное из частей. Таким образом, «система» - нечто заданное, составленное из частей (или чётко расчлененное целое).

Приведите примеры системы (пароход, теплоход, пылесос …).

Знаете ли вы, кому из древних математиков пришла идея о введении системы координат?

(слайд 3) Идея задавать положение точки на плоскости зародилась в древности – прежде всего у астрономов. Во II в. Древнегреческий астроном Клавдий Птолемей пользовался широтой и долготой в качестве координат.

(слайд 4) Слово «абсцисса», «ордината», «координаты» первым начал использовать в конце XVII века немецкий математик Готфрид Лейбниц.

Однажды в 17 в. по дороге из Парижа в Нейбург вечером одинокий путник зашёл на постоялый двор. По кривой скрипучей лестнице путник поднялся на второй этаж бедной гостиницы. Он зашёл в полутёмный номер, снял шпагу и плащ, отпустил слугу, зажёг свечу и сел за дубовый стол. Из дорожной сумки он достал бумагу и гусиное перо с чернильницей. Через какое-то время бумага покрылась таинственными знаками. Скажу по секрету: наш путник был математиком и философом, т.е. человеком, любящим мудрость.

Но в этот день ему не повезло. Формулы, как назло, не сходились, задача не решалась, несмотря на все старания. Ни какой из известных приёмов не подходил. Наконец под утро, отчаявшись, он лёг на тесную кровать, заснул и увидел сон.

Но это был такой сон, который невозможно рассказать, т.к. там не было никакого сюжета. Просто море, огромные волны бились о берег. И вдруг эти остановились. Время как будто замерло. Все вокруг, и сами волны, и морская пена, и облака, быстро бежавшие по небу, вдруг оказались охвачены некой сетью, и в один момент застыли, словно замёрзли … И можно было бродить вдоль этой замёрзшей волны, и видеть там замёрзших рыб … неподвижные водоросли … И можно было все это рассматривать и изучать.

Путник проснулся с каким-то удивительно легким и приятным чувством открытия. Он подошёл к столу, взял перо и нарисовал нечто, подобное сетке из линий. Взглянул на календарь: 10 ноября 1619 год. Открытие состоялось.

А как звали путника, вы узнаете, ответив на вопросы кроссворда.

(слайды 5)

1. Как называют пару чисел, определяющих положение точки на плоскости?

2. Как называются прямые, которые не пересекаются?

3. Как называются прямые, пересекающиеся под углом 90 градусов?

4. Как называют ось ОХ?

5. Какой угол образуют перпендикулярные прямые?

6. Как называют ось ОУ?

координаты

параллельные

перпендикулярные

абсцисс

прямой

ординат

(слайд 6) Рене Декарт родился 31марта 1596г. во Франции.

Происходил из старинного дворянского рода. Учился в колледже, по окончании жил в Париже. Служил в армии, все свое свободное время посвящал науке. Сделал много открытий в физике, создал физическую теорию кровообращения, сделал значительный вклад в области философии.

В 1649 по приглашению шведской королевы Кристины переселился в Стокгольм, где вскоре умер.

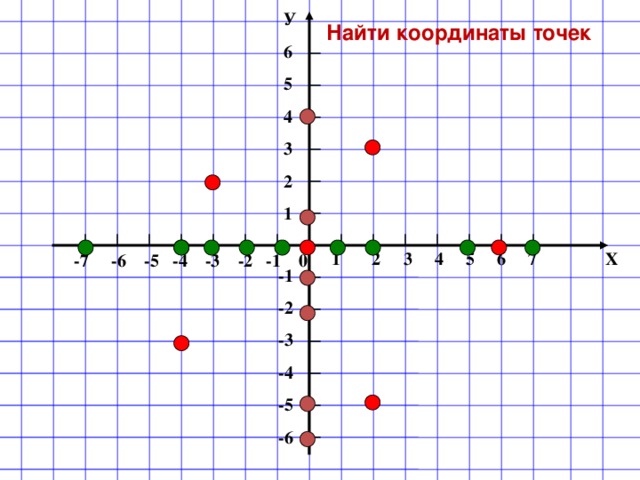
(слайд 7) устная работа.

Определи координату точки.

Что общего у этих точек?
Как задаются точки лежащие на координатных осях? (если точка принадлежит оси ОХ, то (Х; 0), если оси ОУ, то (0;У))

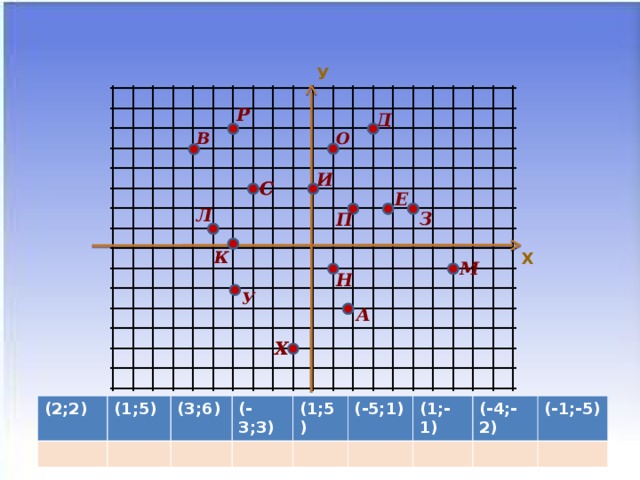
(слайд 8) Расшифруйте слово.

«Стоит Антошка

На одной ножке

Где солнце встанет

Туда он и глянет»

(2;2)	(1;5)	(3;6)	(-3;3)	(1;5)	(-5;1)	(1;-1)	(-4;-2)	(-1;-5)
П	О	Д	С	О	Л	Н	У	Х

(можно взять и это слово – на выбор учителя)

Возле елок из иголок,

Летним днем построен дом.

За травой не виден он,

А жильцов в нем миллион.

(7;-1)	(-4;-2)	(-4;6)	(2;-3)	(-6;5)	(4;2)	(0;3)	(1;-1)	(0;3)	(-4;0)
М	У	Р	А	В	Е	Й	Н	И	К

(слайд 9) Как дитя вселенной, я от всей души постараюсь сделать все, что в моих силах, чтобы нести свет туда, где темно, чтобы нести тепло туда, где холодно. Если я потерплю неудачу, я плакать не буду, а постараюсь вновь. И когда я достигну успехов, моё сердце наполнится светом, теплом, нежностью, любовью.

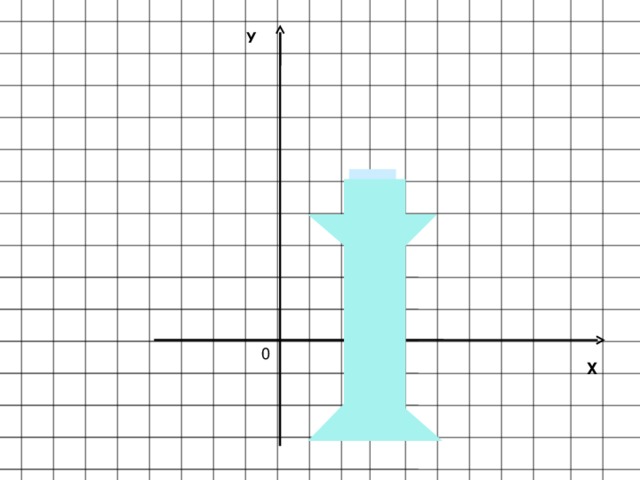
(слайд 10) Давайте зажжем свечу добра. Для этого постройте в системе координат следующие точки (1;-3) (2;-2) (2;3) (1;4) (2;4) (2;5) (4;5) (4;4) (5;4) (4;3) (4;-2) (5;-3) Последовательно соедините эти точки.

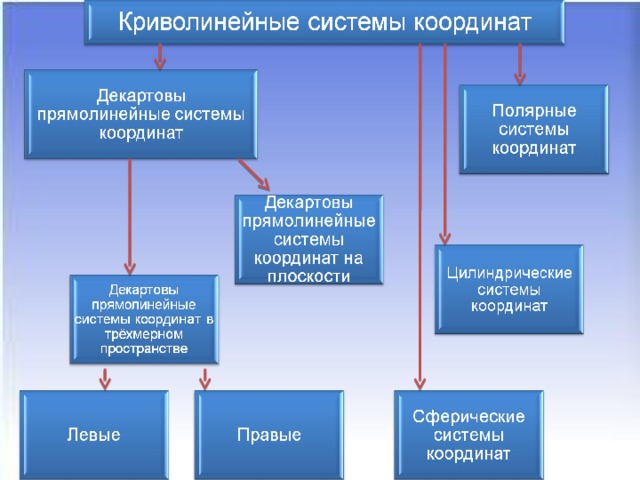
Как вы думаете, существуют ли какие-нибудь системы координат, кроме тех которыми мы пользуемся?

(слайд 11)

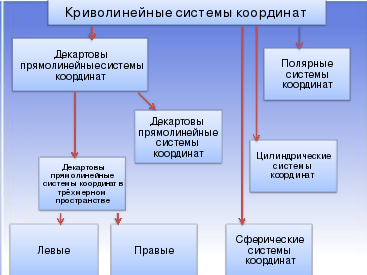
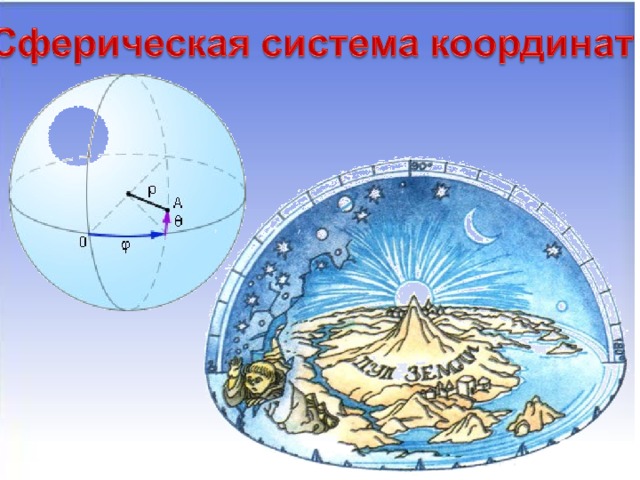
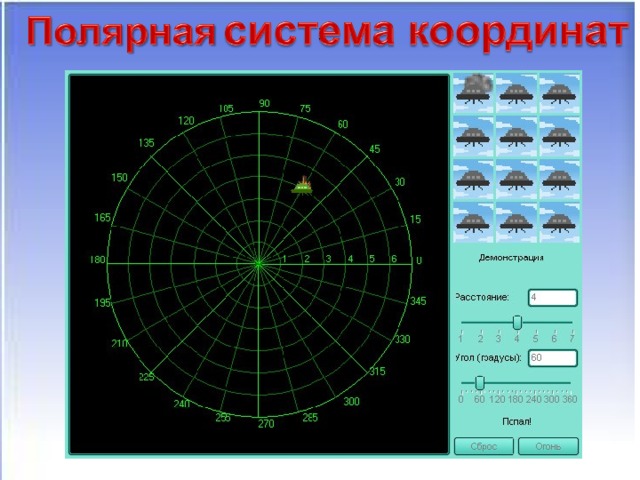
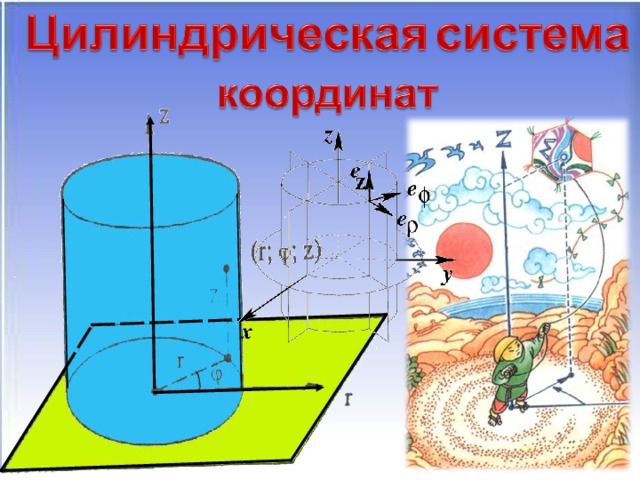
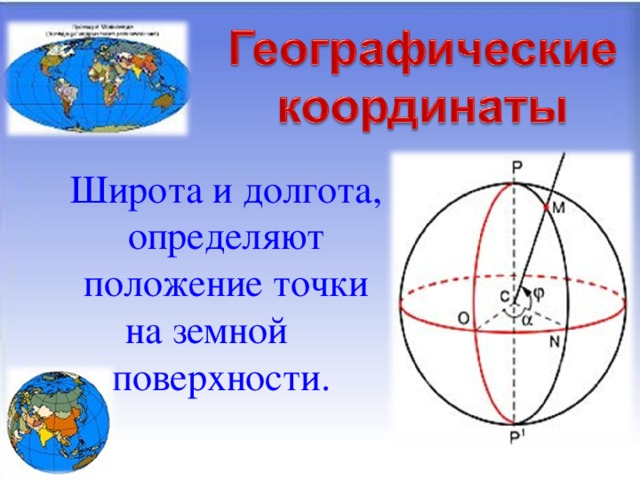
(слайд 12-14) Сферические, полярные, цилиндрические.
(слайд 15) Физкультминутка

Мы руками поведём – будто в море поплывём

Раз, два, три, четыре, вот мы к берегу приплыли.

Чтобы косточки размять, начнем наклоны выполнять.

Вправо – влево, вправо – влево.

Не забудем и присесть –
Раз, два, три, четыре,
На счет пять – за парты сесть

(слайды 16) Школа Робинзона Крузо. Определить вид транспортного средства, которое позволило Робинзону сделать открытие. Нарисуйте фигуру по координатам!

1. (-9;1) (-7;-3) (-7;3) (7;-3) (11;1) (-9;1)

2. (-3;1) (-3;17) (2;16) (-3;15)
3. (-3;1) (1;4) (2;6) (2;9) (1;11) (-3;15)
4. (-3;1) (5;3) (7;5) (8;7) (8;9) (7;11) (5;13) (-3;15)

(слайд 17) Самоконтроль: проверьте, правильно ли вы сделали?

Понятие системы координат встречается даже там, где мы и не думаем, что она есть. Послушайте такие отрывки.

Н.А.Некрасов Кому на Руси жить хорошо

«….. идите по лесу

Против столба тринадцатого

Прямёхонько версту:

Придёте на поляночку,

Стоит на той поляночке

Две стройные сосны …»

К. Симонов «Сын артиллериста» (отрывок)

Третий сигнал по радио.

«Немцы вокруг меня,

Бейте четыре – десять,

Не жалейте меня!»

Майор побледнел, услышав

Четыре – десять – как раз

То место, где его Лёнька

Должен сидеть сейчас.

(слайд 18) Загадки

Шесть ног, а бежит не быстрее, чем на четырех.

(3;-1) (2;-1) (1;0) (1;-2) (-1;-1) (-2;-1) (-4;-2) (-4;1) (-6;1) (-4;3) (-3;1) (-1;3) (-2;4) (-1;5) (0;4) (-1;3) (-1;1) (1;1) (3;-1) всадник на коне

Сижу верхом, не знаю на ком. Знакомца встречу – соскочу, привечу.

(2;0) (1;1) (-1;1) (-2;0) (-2;-1) (-3;-2) (-2;-2) (-1;-1) (2;-1) (2;0) кепка

(слайд 19) Значение координат в нашей жизни. (по гиперссылкам слайды 23-29)

Координаты используются:

в астрономии;
в математике и информатике (построение графиков);
в географии (широта и долгота, определяют положение точки на земной поверхности);
в строительстве;
в кино и театре;
в различных играх;
инженерная графика (Координатные системы разных видов применяют для моделирование эскизов промышленных машин, оборудования, объектов на местности.);

в газетах (для показания роста или спада чего либо) и многом другом…

В современной математике всё чаще пользуются именно представлением своих результатов в графической форме, следуя Декарту. Методы Декарта и других математиков переплетаются, имеют огромную познавательную силу.

(слайд 20) Наш урок хочется закончить такими словами:

Да, много решено загадок

От прадеда и до отца,

И нам с тобой продолжить надо

Тропу, которой нет конца.

В. Наздрёв

(слайд 21) Домашнее задание:Дома я попрошу вас выполнить следующие задания

§6 № 6.26(а, б) 6.40(а).
Нарисовать на координатной плоскости своё ЛЮБИМОЕ ДОМАШНЕЕ ЖИВОТНОЕ. Рисунок, состоящий из ломаных «зашифруйте» с помощью координат точек.

Спасибо за урок. До свидания.

При разработке урока использованы:

Статьи и материалы:

из Википедии — свободной энциклопедии
- (http://ru.wikipedia.org/wiki/)

из Большой энциклопедии Кирилла и Миффодия (www.KM.ru )

материалы сайтов:

http://giscraft.ru, http://dic.academic.ru

http://dovgel.com, http://giscraft.ru nual.ruuztest.ru/abstracts, http://lostlab.ru, maths/geom/coord.php.

Литература:

Труднев В.П. Считай, смекай, отгадывай. — М.: Просвещение, 1980.
Кордемский Б.А. Увлечь школьников математикой. — М.: Просвещение, 1981.
Научно – практический журнал. Математика для школьников № 4, 2012.

Просмотр содержимого презентации
«коорд плос на конкурс»

Мой университет - www . moi - mummi . ru

МБОУ «Тамбовская средняя общеоразовательная школа»

МБОУ «Сидоровская средняя общеобразовательная школа»

Презентацию подготовили:

Учитель математики - Герман Л.А.

Учитель математики и физики – Ященко М.А.

Клавдий Птолемей (др.-греч. Κλαύδιος Πτολεμαος) — знаменитый александрийский астроном, математик и географ II век н. э.

Во II в.

Древнегреческий астроном

Клавдий Птолемей пользовался широтой и долготой в качестве координат

Немецкий философ, физик, математик, историк и дипломат; один из самых универсальных и плодотворных ученых 17 в.

Слова «абсцисса»,

«ордината», «координаты» первым начал использовать в конце XVII века

Лейбниц.

1. Как называют пару чисел, определяющих положение точки на плоскости?

3. Как называются прямые пересекающиеся под углом 90 градусов?

2. Как называются прямые, которые не пересекаются?

4. Как называют ось ОХ?

5. Какой угол образуют перпендикулярные прямые?

6. Как называют ось ОУ?

К О О Р Д И Н А Т Ы

П А Р А Л Л Е Л Ь Н Ы Е

П Е Р П Е Н Д И К У Л Я Р Н Ы Е

А Б С Ц И С С

П Р Я М О Й

О Р Д И Н А Т

К О О Р Д И Н А Т Ы

Французский математик, физик, физиолог и философ, создатель знаменитого метода координат.

Найти координаты точек

1 2 3 4 5 6 7 Х

-7 -6 -5 -4 -3 -2 -1 0

-1

-2

-3

-4

-5

-6

У Р Д В О И С С Е Л З П К К Х М Н У А Х Х (2;2) (1;5) (3;6) (-3;3) (1;5) (-5;1) (1;-1) (-4;-2) (-1;-5)

(2;2)

(1;5)

(3;6)

(-3;3)

(1;5)

(-5;1)

(1;-1)

(-4;-2)

(-1;-5)

Как дитя вселенной, я от всей души постараюсь сделать всё, что в моих силах, чтобы нести свет туда, где темно, чтобы нести тепло туда, где холодно. Если я потерплю неудачу, я плакать не буду, а постараюсь вновь. И когда я достигну успехов, моё сердце наполнится светом, теплом, надеждой и любовью.