Министерство образования и науки Российской Федерации
МБОУ ВОРОНОВСКАЯ СОШ
Урок по математике на тему:
«Теорема Виета»
8 класс
Учитель математики
Первой категории: Пушкарева Г.А.
2015 год
Тип урока: Урок изучение нового материала.
Цель: сформулировать, доказать и научить применять прямую и обратную теорему Виета при решении квадратных уравнений.
Задачи:
Образовательная:
обобщить и систематизировать знания учащихся по теме: «Квадратные уравнения»;
«открыть» зависимость между корнями и коэффициентами приведенного квадратного уравнения;
доказать теорему Виета, сформулировать обратную теорему
учить применять теорему Виета и обратную теорему в различных ситуациях.
Развивающая:
способствовать выработке у школьников умения обобщать изучаемые факты, формулировать выводы;
развивать исследовательские навыки и самостоятельность при составлении и решении уравнений;
Воспитательная:
План урока:
Организационный момент.
Проверка домашнего задания.
Актуализация знаний.
Изучение нового материала.
Первичное закрепление материала.
Итоги.
Домашнее задание.
Ход урока.
Организационный момент.
– Здравствуйте, ребята. Скажите, пожалуйста, какие уравнения мы решали на прошлом уроке?
(Квадратные).
– Сегодня мы продолжим решать квадратные уравнения и познакомимся со знаменитой теоремой, которая поможет нам в их решении.
– Обратите внимание на свои рабочие места. На столе у каждого из вас лежит ваш «Табель», который позволит оценить вашу успешность на этом уроке. Подпишите на нем свою фамилию и имя (См.Приложение 1).
Проверка домашнего задания.
– Дома вы должны были заполнить таблицу. На доске один учащийся заполняет таблицу (См.Приложение 2), а остальные ученики работают с карточками (См.Приложение 3).
Таблица для заполнения на доске. Последние две строчки не заполнены.
| Уравнение | Корни | Произведение корней | Сумма корней |
| 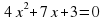
| 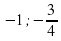
| 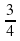
| 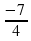
|
| 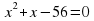
| 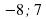
| 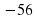
| 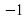
|
| 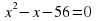
| 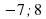
| 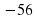
| 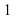
|
| 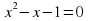
| 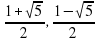
| 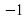
| 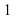
|
| 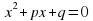
| 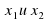
| 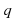
| 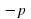
|
| 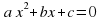
| 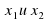
| 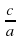
| 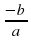
|
На одной из боковой закрытой доске записаны критерии оценок.
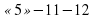
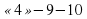
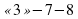
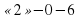
Карточки для учащихся.
| Карточка 1. №1. Сколько корней имеет квадратное уравнение | Решение: |
| а) 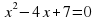 | 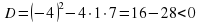 – корней нет – корней нет
|
| б) 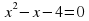 | 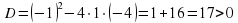 – 2 коня – 2 коня
|
| №2. Решите квадратное уравнение 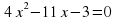
| 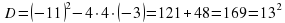
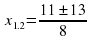
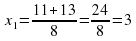
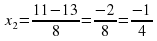
|
| Карточка 2. №1. Сколько корней имеет квадратное уравнение | Решение: |
| а) 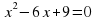 | 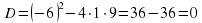 – 1 корень – 1 корень
|
| б) 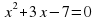 | 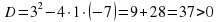 – 2 коня – 2 коня
|
| №2. Решите квадратное уравнение 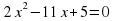
| 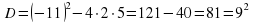
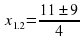
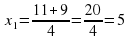
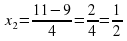
|
– Итак, проверим, как вы справились с таблицей. Поменяйтесь тетрадями с соседом. За каждый верный ответ ставьте «+».
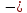 Считаем количество плюсов и выставляем оценки. Максимально можно получить 18 плюсиков. Критерии оценок смотрите на доске (открываем доску после подсчета «+»).
Считаем количество плюсов и выставляем оценки. Максимально можно получить 18 плюсиков. Критерии оценок смотрите на доске (открываем доску после подсчета «+»).
– Далее, проверяем правильность выполнения карточек. (Открываем вторую боковую закрытую доску с решением). Максимум может быть три плюса.
На закрытой доске записаны правильные ответы и критерии оценки.
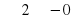
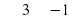

– Поменялись назад тетрадями. Не забудьте выставить свои оценки в ваш табель.
Актуализация знаний.
– Вспомним, какое уравнение называется приведенным?
Уравнение называется приведенным, если коэффициент при старшей степени равен единице.
Изучение нового материала.
–Итак, рассмотрим внимательно заполненную вами таблицу. Не заметили ли вы каких-либо особенностей?
Ответы учеников.
– Давайте сравним с вами сумму и произведение корней с коэффициентами уравнения.
– Сделаем вывод. Какая существует зависимость между корнями приведенного уравнения и его коэффициентами?
– Сформулируйте данное утверждение. Давайте запишем его в тетрадь.
Запись в тетради:
Если приведенное квадратное уравнение имеет корни, то сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Историческая справка.
Впервые зависимость между корнями и коэффициентами квадратного уравнения, установил замечательный французский ученый Франсуа Виет (1540-1603 г.).
Франсуа Виет был по профессии адвокатом и много лет работал советником короля. И, хотя, математика была всего лишь его увлечением, благодаря упорному труду он добился в ней больших результатов.
В 1951 году он ввел буквенные обозначения для коэффициентов при неизвестных в уравнениях, что дало возможность записать общими формулами корни уравнения, а так же его свойства.
Виет сделал множество открытий, среди которых больше всего гордился установлением зависимости между корнями и коэффициентами квадратного уравнения, которое называется теоремой Виета.
Значит, утверждение, которое мы с вами сформулировали, называется теоремой Виета.
– Итак, согласно теореме Виета:
Для приведенного квадратного уравнения 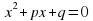

– Давайте докажем это утверждение.
Итак, если 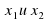 – корни квадратного уравнения
– корни квадратного уравнения 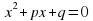 .
.

– Чему равны корни этого уравнения?
и
– Найдем сумму и произведения данных корней.


Итак, согласно теореме Виета для приведенного квадратного уравнения 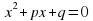

– Необходимо отметить, что теорема Виета применяется только к квадратным уравнениям, имеющим корни.
Первичное закрепление материала.
– Закрепим полученные нами знания на практике. У вас на столе разложены карточки с заданиями и надписью «Закрепление» (См.Приложение 4).
– Рассмотрим первое задание.
№1. Верно ли решены уравнения?
а) - да
б)  - да
- да
в)  -да
-да
г) - да
– На основании чего вы можете утверждать, что данные числа являются корнями уравнения?
– Почему вы так решили?
(Согласно теореме Виета)
– Можно ли определить знаки корней уравнения, не решая его?
(Да)
– Следующий номер выполните самостоятельно, затем мы с вами проверим его.
№2. Составьте квадратные уравнения, корнями которого являются числа.
– Какое утверждение мы использовали в данном случае?
(Сумма корней равна второму коэффициенту с противоположным знаком, произведение корней равно свободному члену).
– Давайте немного отдохнем.
– Кстати, огромную славу Франсуа Виет приобрел во время франко-испанской войны, подобрав ключ к необыкновенной испанской тайнописи. Испанские инквизиторы обвинили французов в сговоре с дьяволом, так как по их мнению, только дьявол мог разгадать их хитроумный шифр.
– Продолжим работу.
№3. Какая пара чисел является корнями уравнения  .
.

– Почему?
(Так как  , то есть
, то есть  )
)
Значит, мы можем сделать следующий вывод. Если  , то эти числа являются корнями приведенного квадратного уравнения
, то эти числа являются корнями приведенного квадратного уравнения 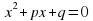
– Данное утверждения является обратным для теоремы Виета. Его доказательством вы займетесь дома самостоятельно.
– Используя это утверждение, решим задание №4.
№4. Найдите подбором корни квадратного уравнения.
а) 
б) 
в) 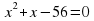
г) 
Решение:
а) 
б) 
в) 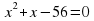
г) 
Задание решается на доске учениками.
– Значит, для решения данного задания мы использовали утверждение, обратное теореме Виета.
– Решим с вами следующую задачу.
На доске было записано уравнение  . Кто-то из учеников стер свободный член. Вместо свободного члена я поставила букву
. Кто-то из учеников стер свободный член. Вместо свободного члена я поставила букву  . Я знаю, что один из корней уравнения равен 2. Какое уравнение было написано первоначально?
. Я знаю, что один из корней уравнения равен 2. Какое уравнение было написано первоначально?
Задачу у доски решает ученик.
– Что нам надо использовать при решении данной задачи?

 = уравнение выглядит так
= уравнение выглядит так  .
.
– Вернемся к таблице и заполним предпоследнюю строку Над заполнением последней строки вы должны поработать дома.
– Оцените, пожалуйста, свою работу с заданиями на закрепление и поставьте себе оценку в табель.
Итоги.
– Итак, подведем итоги сегодняшнего урока.
– Сегодня мы с вами познакомились с теоремой знаменитого французского ученого Франсуа Виета и научились её применять при решении простейших задач.
– Где же применяется теорема Виета?
– Можно проверить, правильно ли найдены корни квадратного уравнения?
– Как можно определить знаки корней квадратного уравнения, не решая его?
– Можно ли определить знаки корней квадратного уравнения, не решая его?
– Закончить урок мне хотелось бы такими словами:
«По праву достойна в стихах быть воспета,
О свойствах корней теорема Виета».
Домашнее задание.
–Запишите домашнее задание.
П.23, №582(а,в,д), 584, 585, 597.
 Табель
Табель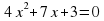
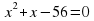
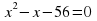
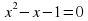
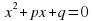
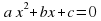
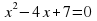 б)
б) 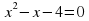
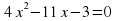
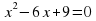 б)
б) 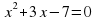
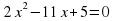
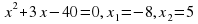
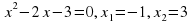
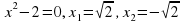
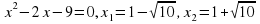
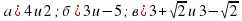
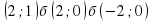 является корнями уравнения
является корнями уравнения 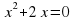 .
.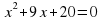
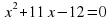
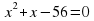
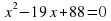
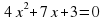
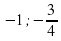
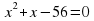
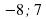
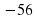
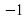
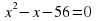
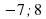
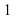
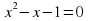
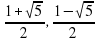
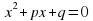
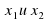
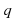
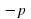
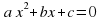
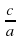
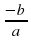
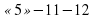
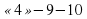
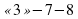
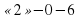
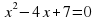
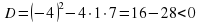 – корней нет
– корней нет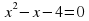
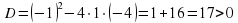 – 2 коня
– 2 коня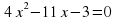
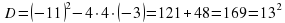
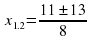
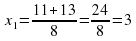
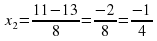
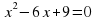
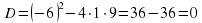 –
– 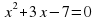
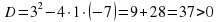 – 2 коня
– 2 коня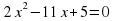
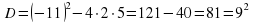
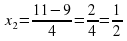
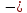 Считаем количество плюсов и выставляем оценки. Максимально можно получить 18 плюсиков. Критерии оценок смотрите на доске (открываем доску после подсчета «+»).
Считаем количество плюсов и выставляем оценки. Максимально можно получить 18 плюсиков. Критерии оценок смотрите на доске (открываем доску после подсчета «+»).