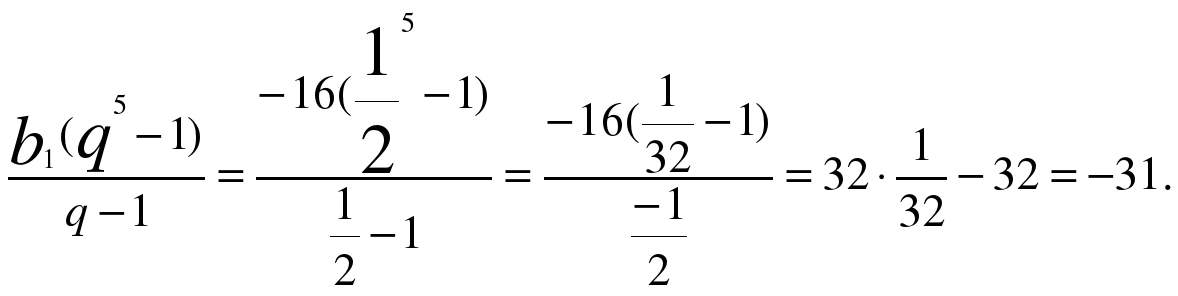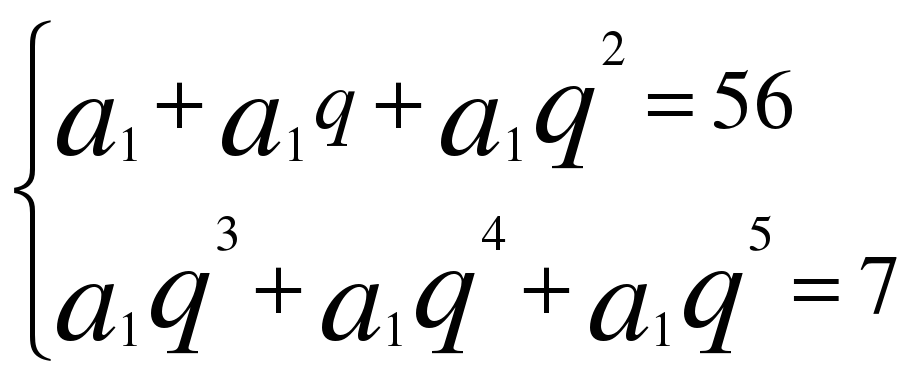Повторительно-обобщающий урок по теме: « Арифметическая и геометрическая прогрессии»

Цели:
- Повторить и обобщить знания по теме «Арифметическая и геометрическая прогрессия».
- Расширить знания.
- Совершенствовать навыки решения задач.
- Установить уровень знаний и умений по теме.


Учет результатов работы
Этапы:
Этапы:
Оценка
или
кол-во баллов
Прогнозируемая оценка по теме
Оценка
или
кол-во баллов
Прогнозируемая оценка по теме
5
I. Проверка теории
I. Проверка теории
II . Экспресс - опрос
II . Экспресс - опрос
10
III . Тест – прогноз
III . Тест – прогноз
6
3
Дополнительные баллы
Дополнительные баллы
Всего баллов за урок
4
Всего баллов за урок
23
Оценка за урок
Оценка за урок

I. Проверка теории
Арифметическая прогрессия
1. Определение
(реккурентная формула)
Геометрическая прогрессия
2. Формула n- ого члена
3. Сумма первых n членов
прогрессии
4. Свойства

Заполненная таблица
Арифметическая прогрессия
1. Определение
(реккурентная формула)
2. Формула n- ого члена
Геометрическая прогрессия
3. Сумма первых n членов
прогрессии
4. Свойства

Этапы:
Оценка
или
кол-во баллов
Прогнозируемая оценка по теме
5
I. Проверка теории
10
II . Экспресс - опрос
III . Тест – прогноз
Дополнительные баллы
Всего баллов за урок
Оценка за урок


Связь прогрессий
a n =a n-1 +d
а n =a n-1 · q
a n =a 1 · q n -1
a n =a 1 +d(n-1)

Прогрессио – это …

II. Экспресс-опрос
Вариант 1.
I . Дано ( b n ) : ⅓; 1;… - геометрическая прогрессия.
1. Найдите знаменатель прогрессии.
2. Найдите четвертый член прогрессии.
3. Найдите сумму 4-х первых членов прогрессии.
4. Найдите сумму всех членов геометрической прогрессии, если b 1 =48, q = - ½.
II . Дано ( a n ) : 10; 7; … - арифметическая прогрессия.
1. Найдите разность прогрессии.
2. Найдите десятый член прогрессии.
3. Найдите сумму 10-и первых членов прогрессии.
Вариант 2.
I . Дано ( b n ) : ½; 1; … - геометрическая прогрессия
1. Найдите знаменатель прогрессии.
2. Найдите пятый член прогрессии.
3. Найдите сумму 5-и первых членов прогрессии.
4. Найдите сумму всех членов геометрической прогрессии, если b 1 =36, q = - ½.
II . Дано ( a n ) : 15; 10 ; … - арифметическая прогрессия.
1. Найдите разность прогрессии.
2. Найдите двенадцатый член прогрессии.
3. Найдите сумму 12-и первых членов прогрессии.
- Вариант 2. I . Дано ( b n ) : ½; 1; … - геометрическая прогрессия 1. Найдите знаменатель прогрессии. 2. Найдите пятый член прогрессии. 3. Найдите сумму 5-и первых членов прогрессии. 4. Найдите сумму всех членов геометрической прогрессии, если b 1 =36, q = - ½. II . Дано ( a n ) : 15; 10 ; … - арифметическая прогрессия. 1. Найдите разность прогрессии. 2. Найдите двенадцатый член прогрессии. 3. Найдите сумму 12-и первых членов прогрессии.
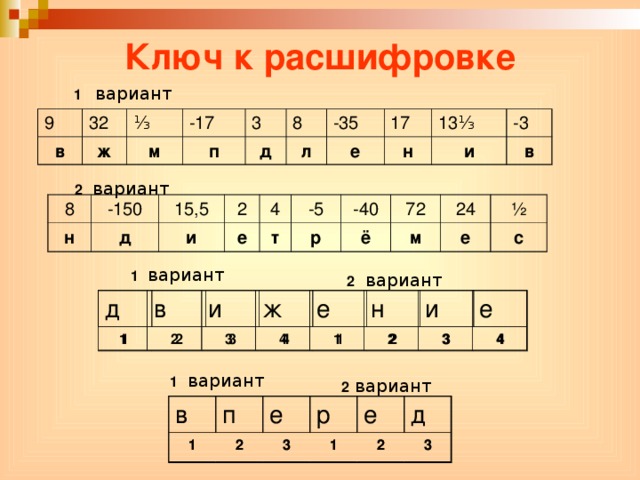
Ключ к расшифровке
1 вариант
9
32
в
ж
⅓
м
-17
п
3
д
8
л
-35
е
17
н
13⅓
и
-3
в
2 вариант
8
-150
н
д
15,5
и
2
е
4
т
-5
р
-40
ё
72
м
24
е
½
с
1 вариант
2 вариант
д
в
1
1
и
2
2
ж
3
3
е
4
4
1
н
1
и
2
2
е
3
3
4
4
1 вариант
2 вариант
в
1
1
п
2
2
е
3
р
3
е
1
1
2
2
д
3
3

Этапы:
Оценка
или
кол-во баллов
Прогнозируемая оценка по теме
5
I. Проверка теории
10
II . Экспресс - опрос
6
III . Тест – прогноз
IV . Дополнительные баллы
Всего баллов за урок
Оценка за урок

Прогрессио – движение вперед!
- будешь как я!

А знаете ли вы, что…
- В клинописных табличках вавилонян, как и в египетских папирусах, относящихся ко 2 тысячелетию до нашей эры, встречаются примеры арифметической и геометрической прогрессий. В основном это были задачи о разделе наследства, о распределении продуктов, в общем, задачи, связанные с запросами хозяйственной жизни и общественной практики.
- 5 век до н.э. – древние греки знают формулы суммы натуральных и четных натуральных последовательных чисел.
- 5 век н.э. – в Китае и Индии ученые знают формулу n -ого члена и суммы n первых членов арифметической прогрессии.
- Упоминание о геометрической прогрессии в легенде об изобретателе шахмат.

Задача №1
- Юноша подарил девушке в первый день 3 цветка, а в каждый последующий день дарил на 2 цветка больше, чем в предыдущий день. Сколько денег он потратил на цветы за две недели, если один цветок стоит 10 рублей?
- Юноша подарил девушке в первый день 3 цветка, а в каждый последующий день дарил на 2 цветка больше, чем в предыдущий день. Сколько денег он потратил на цветы за две недели, если один цветок стоит 10 рублей?

Решение
1. Пусть (кол-во цветов, купленных в 1-ый день), тогда (на столько юноша увеличивал каждый день кол-во купленных цветков).
2. Найдем (кол-во цветков, купленных за две недели):
3. Найдем количество потраченных денег на цветы:
(руб)
Ответ: юноша потратил за две недели 2240 рублей.

Задача №2.
Родители ко Дню рождения своего сына Андрея решили купить и обновить ему мобильный телефон.
Для этого они в первый месяц отложили 650 рублей, а в каждый последующий месяц они откладывали на 50 рублей больше, чем в предыдущий.
Какая сумма будет у родителей Андрея через 10 месяцев?

Дано:
Найти:
Решение:
Ответ: 8750 рублей.

Этапы:
Оценка
или
кол-во баллов
Прогнозируемая оценка по теме
5
I. Проверка теории
10
II . Экспресс - опрос
6
III . Тест – прогноз
Дополнительные баллы
4
Всего баллов за урок
Оценка за урок

III. Тест-прогноз
В геометрической прогрессии ( c n ) c 2 =8, c 4 =2.
В геометрической прогрессии ( b n ) b 3 =3, b 5 =⅓.
1. Найдите знаменатель прогрессии. (1балл)
- 1. Найдите знаменатель прогрессии. (1балл)
1. Найдите знаменатель прогрессии, если известно, что все ее члены положительны. (1балл)
2. Найдите первый член этой прогрессии. (1балл)
3. Найдите сумму 6-и первых членов прогрессии. (1балл)
- 1. Найдите знаменатель прогрессии, если известно, что все ее члены положительны. (1балл) 2. Найдите первый член этой прогрессии. (1балл) 3. Найдите сумму 6-и первых членов прогрессии. (1балл)
2. Найдите первый член прогрессии, если известно, что члены последовательности с нечетными номерами – отрицательны, а с четными номерами – положительны. (1балл)
3. Найдите сумму 6-и первых членов прогрессии. (1балл )
- 2. Найдите первый член прогрессии, если известно, что члены последовательности с нечетными номерами – отрицательны, а с четными номерами – положительны. (1балл) 3. Найдите сумму 6-и первых членов прогрессии. (1балл )

Тест-прогноз. Ответы:
№ задачи
1.
I вариант
2.
II вариант
3.
-16
-10,5
27

Решение первой задачи
Дано: (с n ) – геом. прогрессия
с 2 = 8; с 4 = 2
Найти: q
Решение:
с 4 = с 2 * q 2
q 2 = c 4 / c 2
q 2 = 2/8 = ¼
q 1 = ½
q 2 = - ½
Дано: ( b n ) – геом. прогрессия
b 3 = 3 ; b 5 = ⅓
Найти : q , если все члены ( b n ) положительны
Решение:
b 5 = b 3 * q 2
q 2 = b 5 / b 3
q 2 = ⅓ : 3 = 1/9
q 1 = ⅓
q 2 = - ⅓
т.к. все члены ( b n ) положительны, то q = ⅓

Решение второй задачи
Дано: (с n ) – геом. прогрессия
с 2 = 8; q 1 = ½ ; q 2 = - ½
Найти: с 1
Решение:
1 ) .Т.к. члены (с n ) имеют разные знаки, то
q = - ½
2 ) . с 2 = с 1 *q
с 1 = с 2 : q
с 1 = 8 : (-½) = -16
Дано: ( b n ) – геом. прогрессия
b 3 = 3 ; q = ⅓ ;
Найти: b 1
Решение:
b 3 = b 1 *q 2
b 1 = b 3 : q 2
b 1 = 3 : ( ⅓ ) 2 = 3 : 1/9 = 27

Решение третьей задачи вариант 1
Дано: (с n ) – геом. прогрессия
с 1 = -16; q = - ½
Найти: S 6
Решение:

Решение третьей задачи вариант 2
Дано: ( b n ) – геом.
прогрессия
b 1 = 27; q = ⅓ ;
Найти: S 6
Решение:
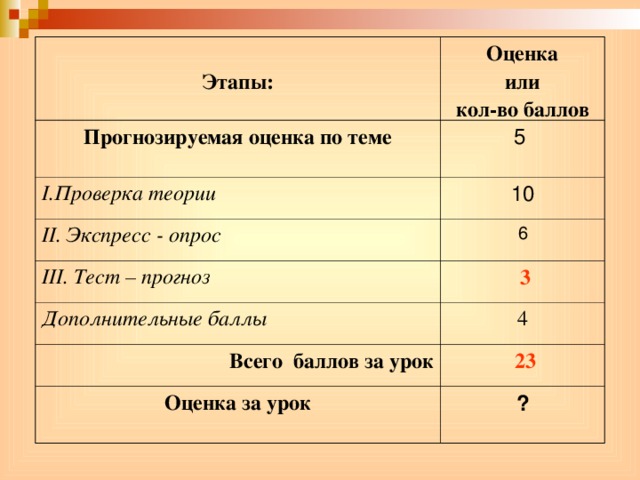
Этапы:
Оценка
или
кол-во баллов
Прогнозируемая оценка по теме
5
I. Проверка теории
10
II . Экспресс - опрос
6
III . Тест – прогноз
3
Дополнительные баллы
4
Всего баллов за урок
2 3
Оценка за урок
?
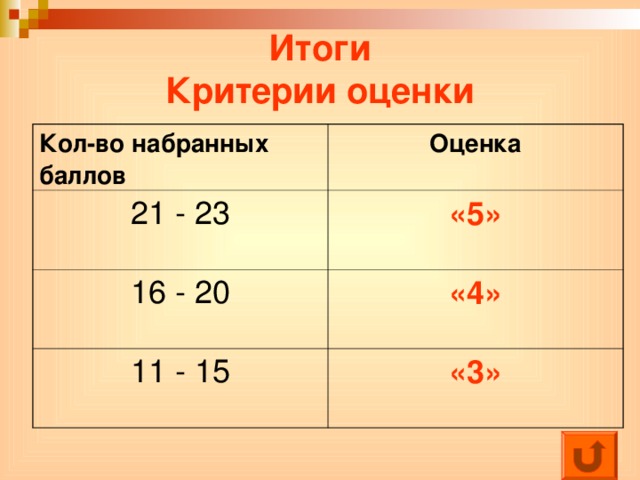
Итоги Критерии оценки
Кол-во набранных баллов
Оценка
21 - 23
«5»
16 - 20
«4»
11 - 15
«3»






Спасибо
за урок!
 ,
,
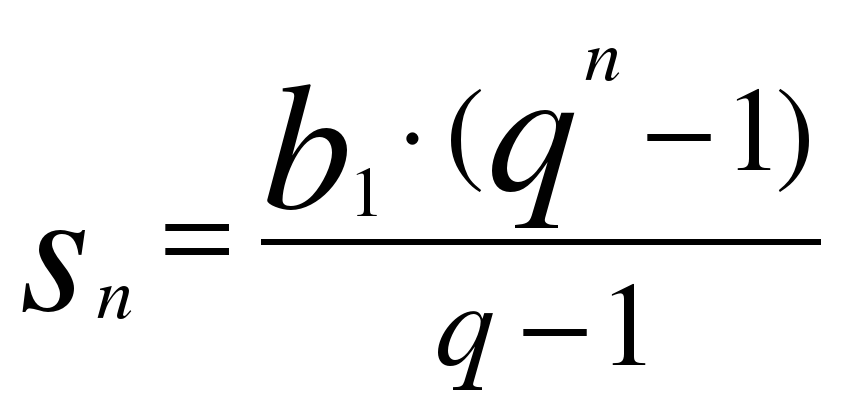 ,
, 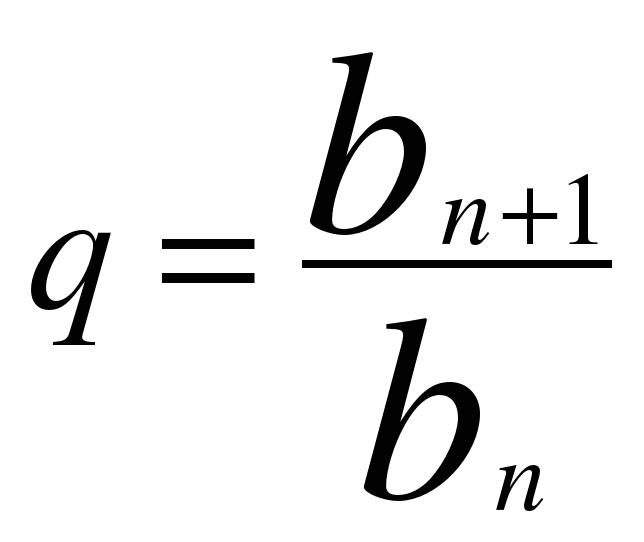
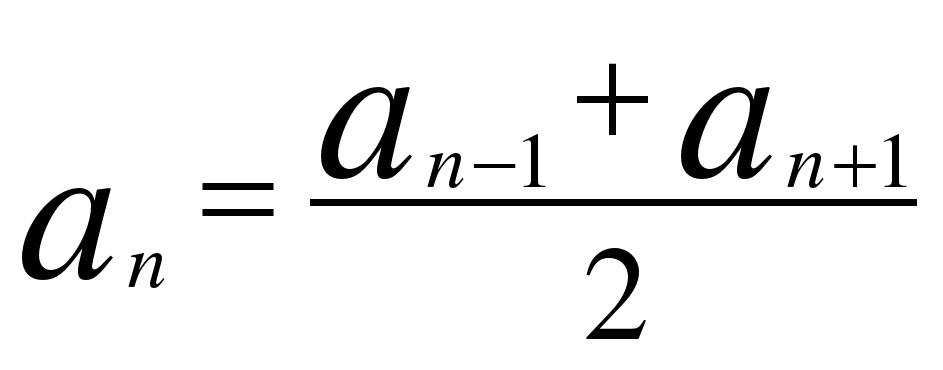

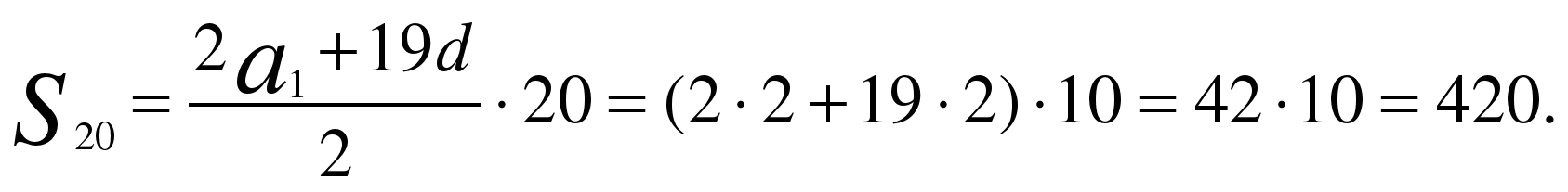
 ,
,