Разработка урока по алгебре для 9 класса по теме "Арифметическая и геометрическая прогрессии"

Разработка урока по алгебре для 9 класса по теме "Прогрессии". Тип урока - обобщение и систематизация знаний. Данный урок нацелен на обобщение и систематизацию знаний учащихся по арифметической и геометрической прогрессиям. Способствует развитию навыков применения основных формул для решения задач. В структуре урока содержатся задания для повторения формул, решение задач, исследовательская работа, сообщения учащихся по теме урока. В ходе урока прослеживается интеграция с историей и литературой. К разработке прилагается презентация.

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«ОТКРЫТЫЙ УРОК ПО ПРОГРЕССИЯМ»

КГУ «Маяковская средняя школа отдела образования акимата Алтынсаринского района»

Открытый урок

Тема: «Арифметическая и геометрическая прогрессии»

Алгебра 9 «Б» класс

Урок подготовила и провела:

учитель математики

Кутенко Т.В.

Январь 2015 год

с.Первомайское

Открытый урок по алгебре

Тема: «Арифметическая и геометрическая прогрессии»

Класс: 9 «Б»

Тип урока: урок обобщения и систематизации знаний.

Цель:

Обобщить и систематизировать знания по арифметической и геометрической прогрессии;

2.Способствовать развитию навыков применения основных формул в ходе решения задач;

3. Воспитать волю и настойчивость для достижения конечных результатов.

Оборудование: мультимедийное оборудование, ватманы, цветные маркеры, рабочее поле для каждого ученика, листы ответов.

Структура урока:

Этапы урока

Содержание работы

Продолжительность, мин

Задачи, решаемые на этапах урока

Вводный

Оргмомент

Установочный

Актуализация знаний:

Фронтальный опрос определений

Основные формулы прогрессии

Определение прогрессий по слайдам

Решение задач (работа в парах)

Коррекция ЗУН.

Мотивация дальнейшей деятельности.

Закрепление знаний.

Определение последовательности промежуточных этапов с учетом конечного результата.

Основной

Роль прогрессий в повседневной жизни

Работа в группах. Решение задач (мини-исследование)

Отчеты групп

Выступления учащихся

Создание условий эффективной и рациональной деятельности учащихся и учителя.

Развитие интереса к математике.

Формирование коммуникативных действий: общение, умение вступать в диалог, инициативное сотрудничество.

Моделирование с целью выяснения общих законов.

Контролирующий

Самостоятельная работа

Проверка самостоятельной работы

7-8

Создание условий для индивидуальной работы. Выявление уровня учебных достижений. Коррекция ЗУН

Итоговый

Рефлексия. Домашнее задание

Рефлексия способов и условий действия, полученных результатов

РЕЗЕРВ: Задачи на концентрацию внимания

Ход урока

Организационный момент.

Учитель: Здравствуйте ребята, садитесь. Сегодня у нас с вами открытый урок. У нас присутствуют гости. Поэтому для того, чтобы снять напряжение и не волноваться, я предлагаю начать наш урок с высказывания:

«Человек страшится только того, чего не знает. Знанием побеждается страх» (слайд №2)

Учитель: Я желаю вам сегодня максимально проявить знания!

Учитель: Сегодня мы заканчиваем изучение темы «Последовательности». (слайд №1) На уроках познакомились с возрастающими, убывающими, ограниченными, неограниченными последовательностями, но особое внимание удели двум последовательностям, каким?

Ученик: Арифметическая и геометрическая последовательности.

Учитель: этим последовательностям дали имена и сказали о них: «Прогрессии».

Что означает слово «Прогрессия»? (слайд №3)

Ученик: Движение вперед.

Учитель: Сегодня мы будем двигаться вперед и убедимся, что раздел математики «Прогрессии» является неотъемлемой частью общечеловеческой культуры и окружающего нас Мира.

Актуализация знаний учащихся.

1. Ответим устно на вопросы:

- Какую прогрессию называют арифметической?

- Какую прогрессию называют геометрической?

- Как найти разность арифметической прогрессии?

- Как найти знаменатель геометрической прогрессии?

- Назовите формулу n -го члена арифметической прогрессии. Что в формуле обозначает n?

-Назовите формулу n -го члена геометрической прогрессии.

2. Давайте вспомним формулы. Посмотрите на слайд и соотнесите формулы в нужные столбцы. (слайд №5 )

Арифметическая прогрессия: a_n=a₁+d(n-1); a_n=k_n+b; S_n= (a₁+a_n)n\2; d=a_n+1-a_n

Геометрическая прогрессия: S_n=b_nq-b₁\q-1 ; q=b_n-1\b_n; a_n=a₁q_n-1

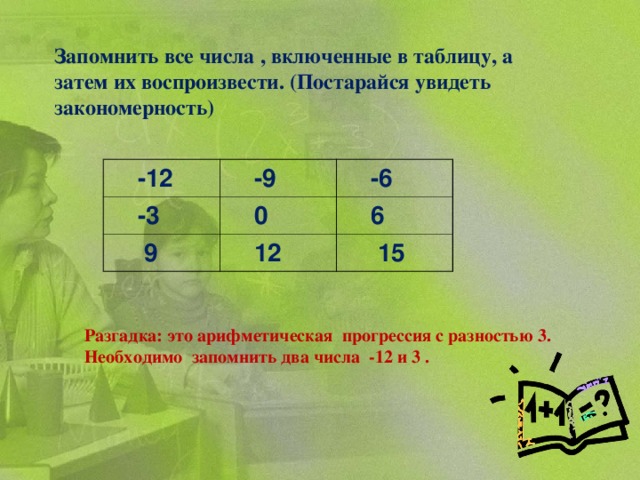
3. Перед вами несколько числовых последовательностей. Выберите те, которые являются арифметической прогрессией и найдите ее разность; те, которые являются геометрической прогрессией и найдите ее знаменатель. Для этого заполните небольшую таблицу в бланках ответов. (Дается время 2мин.). (слайд №6)

Арифметическая последовательность	Геометрическая последовательность
-2; 0;2; …	-4; -8; -16;…
8; 6; 4;…	7; 14;28;…

-2; 0; 2; 4;……
-4; -8; -16;……
7; 14; 28; 56;…
8; 6; 4;…….

Сверяем свои ответы и оцениваем себя. (Слайд №7).

4. Решение задач . Работа в парах.(слайды № 8,9)

А) Поезд отойдя от станции равномерно увеличивал скорость на 50 м в минуту. Какова была скорость поезда в конце 21 минуты ? (эта задача на арифметическую или геометрическую прогрессию?)

Решение: а₂₁=а₁+d(n-1)==50+50*20=1050м

Б) Подготовку к экзамену начинают с 15 мин. В каждый следующий день её время увеличивают на 10 мин. Сколько дней следует готовиться к экзамену в указанном режиме, чтобы достичь максимальной продолжительности подготовки, не влияющей на здоровье подростка, 1час 45минут ?

Дано: a₁=15 Решение: a_n=a₁+(n-1)d

d=10 a_n=a₁+nd-d

a_n=105 nd=a_n-a₁+d

Найти: n

10n=105-15+10

10n=100

n=10

Обобщение и систематизация знаний.

Исследовательская работа. Работа в группах.

Учитель: Когда мы начинали изучать геометрическую прогрессию, я вам рассказывала легенду об изобретении шахматной доски. Но мы не решали эту задачу. Сегодня мы с вами проведем небольшое исследование и решим эту задачу. Работаем в группах. Решение оформляем на ватманах. (приложение 2) (слайды 10-13)

Учитель: А сейчас мы немного передохнем, и послушаем выступления ваших одноклассников о том, действительно ли прогрессии играют большую роль в повседневной жизни?

Выступления учащихся (Презентации Вики Бородулиной, Карины Достьяровой и Мадины Башпеновой)

Учитель: Вы убедились, что раздел математики «Прогрессии» являются неотъемлемой частью общечеловеческой культуры?

Учитель: Сейчас вам необходимо показать свои знания по этой теме и выполнить индивидуальную самостоятельную работу. (7-8мин.)

Самостоятельная работа (тесты) с последующей проверкой (слайд №15-17)

Учитель: Самостоятельная работа пройдет под девизом

«Гений состоит из 1 процента вдохновения и 99 процентов потения» Т. Эдисон (слайд №14)

Прогрессии.

I вариант

Найдите разность арифметической прогрессии (с_n), если с₅ =7, а с₇ =13

А) 2

Б) 3

В) -2

Г) другой ответ

Чему равна сумма первых пяти членов геометрической прогрессии (b_n),

если b₁ = l, а знаменатель равен -2?

А) 11

Б) -17

В) 17

Г) другой ответ

Найдите сумму первых пяти членов арифметической прогрессии (a_n),

если a₁ =6, a₅ = - 6.

А) 30

Б) 5

В) 0

Г) 1

Чему может быть равен знаменатель геометрической прогрессии (b_n),

если b₁₀ = l0, а b₁₂ = 40?

А) 2

Б) ±2

В) 4

Г) 15

В арифметической прогрессии (с_n) разность равна -0,3, а с₁=8. Найдите все натуральные n, при которых выполняется неравенство: с_n 4,6?

А) n

Б) n

В) n

Г) n

Найдите сумму бесконечной геометрической прогрессии (a_n),

если a₁ =3, a₂ = 0,3 .

А)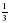

Б)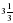

В)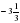

Г) 1

В арифметической прогрессии (a_n), найдите a_7,если a₃+ a₁₁ =20.

А) 5

Б) 10

В) 20

Г) другой ответ

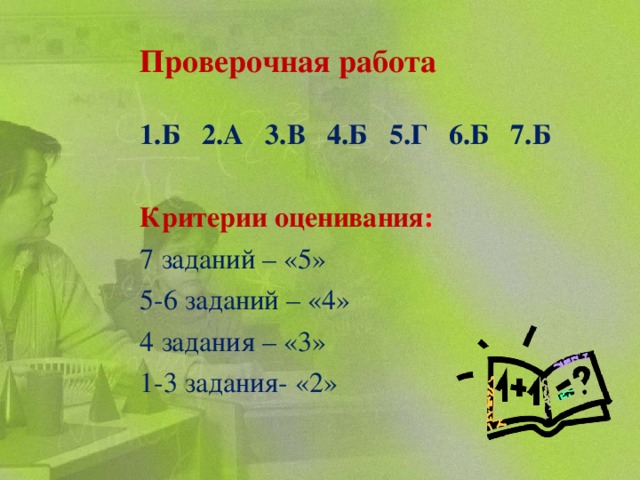
Проверочная работа (тест)

Подведение итогов урока. Рефлексия.

Итак, ребята, наш урок подошел к концу.

-Что мы сегодня на уроке с вами повторили?

-Что нового узнали? (Обсуждение)

Завершить наш урок хочу такими словами: (слайд № 18)

Урок сегодня завершен,

Но каждый должен знать:

Познание, упорство, труд

К прогрессу в жизни приведут!

Домашнее задание. Подготовить исследовательскую работу по теме: Что выгоднее? (1000000 тенге прямо сейчас или 1тиын ежедневно удваивающийся в течение 30 дней? ) (слайд 19)

^{Результаты исследовательской деятельности представить в виде:
-буклета;
-презентации.}

Выставление оценок. Весь урок учащиеся выставляют себе оценки за каждый этап в оценочных листах, затем считают результаты и оглашают их.

ПРИЛОЖЕНИЕ

Рабочее поле

Учени___ 9 «Б» класса____________________________________

Заполнить таблицу

1.-2; 0;2; 4;…

2.-4; -8; -16;…

3.7; 14;28;56;…

4.8; 6; 4;…

Арифметическая прогрессия	Геометрическая прогрессия

Решение задач.

Решение:

Ответ:

Решение:

Ответ:

Задача :

Самостоятельная работа. (тест)

Прогрессии.

I вариант

Найдите разность арифметической прогрессии (с_n), если с₅ =7, а с₇ =13

А	Б	В	Г
2	3	-2	другой ответ

Чему равна сумма первых пяти членов геометрической прогрессии (b_n), если b₁ = l, а знаменатель равен -2?

А	Б	В	Г
11	-17	17	другой ответ

Найдите сумму первых пяти членов арифметической прогрессии (a_n), если a₁ =6, a₅ = - 6.

А	Б	В	Г
30	5	0	1

4. Чему может быть равен знаменатель геометрической прогрессии (b_n), если b₁₀ = l0, а b₁₂ = 40?

А

Б

В

Г

2

±2

4

15
В арифметической прогрессии (с_n) разность равна -0,3, а с₁=8. Найдите все натуральные n, при которых выполняется неравенство: с_n 4,6?

А

Б

В

Г

n

n

n

n
Найдите сумму бесконечной геометрической прогрессии (a_n), если a₁ =3,

a₂ = 0,3 .

А	Б	В	Г
			1

В арифметической прогрессии (a_n), найдите a_7,если a₃+ a₁₁ =20.

А	Б	В	Г
5	10	20	другой ответ

Оценочный лист

Ф.И. ученика_________________________________________________

№ задания	Своя оценка	Оценка учителя
1
2
3
4
5

Оценочный лист

Ф.И. ученика_________________________________________________

№ задания	Своя оценка	Оценка учителя
1
2
3
4
5

Оценочный лист

Ф.И. ученика_________________________________________________

№ задания	Своя оценка	Оценка учителя
1
2
3
4
5

Просмотр содержимого презентации
«презентация к уроку»

КГУ «Маяковская средняя школа отдела образования акимата Алтынсаринского района »

Открытый урок

Алгебра 9 класс

Тема: «Арифметическая и геометрическая прогрессии»

Кутенко Т.В.

учитель математики

«Человек страшится только того, чего не знает. Знанием побеждается страх»

Цель:

1. Обобщить и систематизировать знания по арифметической и геометрической прогрессии;

2.Способствовать развитию навыков применения основных формул в ходе решения задач;

3. Воспитать волю и настойчивость для достижения конечных результатов.

$Среди перечисленных формул выберите те, которые относятся к арифметическим и геометрическим прогрессиям Геометрическая прогрессия Арифметическая прогрессия а n =a 1 +d(n-1) S n =b n q-b 1 \q-1 q=b n -1\b n a n =k n +b S n = (a 1 +a n )n\2 d=a n+1 -a n a n =a 1 q n-1$

Среди перечисленных формул выберите те, которые относятся к арифметическим и геометрическим прогрессиям

Геометрическая прогрессия

Арифметическая прогрессия

а n =a 1 +d(n-1)

S n =b n q-b 1 \q-1

q=b n -1\b n

a n =k n +b

S n = (a 1 +a n )n\2

d=a n+1 -a n

a n =a 1 q n-1

a n =a 1 q n-1

-2; 0;2; 4;… -4; -8; -16;… 7; 14;28;56;… 8; 6; 4;…

-2; 0;2; 4;…
-4; -8; -16;…
7; 14;28;56;…
8; 6; 4;…

Арифметическая последовательность

Геометрическая последовательность

-2; 0;2; …

-4; -8; -16;…

8; 6; 4;…

7; 14;28;…

Поезд отойдя от станции равномерно увеличивал скорость на 50 м в минуту. Какова была скорость поезда в конце 21 минуты ? (эта задача на арифметическую или геометрическую прогрессию?)

а 21 =а 1 +d(n-1)==50+50*20=1050м

Подготовку к экзамену начинают с 15 мин. В каждый следующий день её время увеличивают на 10 мин. Сколько дней следует готовиться к экзамену в указанном режиме, чтобы достичь максимальной продолжительности подготовки, не влияющей на здоровье подростка, 1час 45минут?

Дано: a 1 =15 d=10 a n =105

Найти: n

Решение: a n =a 1 +(n-1)d

a n =a 1 +nd-d

nd=a n -a 1 +d

10n=105-15+10

10n=100 n=10

Ответ: 10 дней

ЛЕГЕНДА

О ШАХМАТНОЙ ДОСКЕ

Древнеиндийский царь Шерам пожелал наградить изобретателя шахмат древнеиндийского ученого Сету.

-« Я достаточно богат, чтобы исполнить любое твое пожелание, проси, что хочешь» заявил самонадеянный царь.

-«Прикажи выдать за первую клетку шахматной доски одно пшеничное зерно, за вторую прикажи дать два зерна, за третью-четыре, за четвертую- восемь, за пятую …» .

-«Довольно, ты получишь зерна за все 64 клетки доски согласно твоему желанию, просьба твоя ничтожна, слуги принесут тебе твою пшеницу…» раздраженно сказал самоуверенный царь Шерам .

Ученый Сета улыбнулся, поклонился и ушел дожидаться обещанной награды . Наутро царь осведомился у слуг, доставлена ли награда изобретателю.

-« О повелитель, число зёрен было так велико…»

«Как бы оно не было велико, награда должна быть выдана, не жалейте амбаров с зерном»- надменно сказал царь.
«Не в твоей власти исполнять такие желания, во всех твоих амбарах и на полях , и на всей Земле нет такого числа зерен, которое потребовал ученый Сета» - ответили слуги.
«Назовите это чудовищное число!»- воскликнул

изумленный царь.

«ГЕНИЙ СОСТОИТ ИЗ 1 ПРОЦЕНТА ВДОХНОВЕНИЯ И 99 ПРОЦЕНТОВ ПОТЕНИЯ». Т. ЭДИСОН

Самостоятельная работа 1. Найдите разность арифметической прогрессии (с n ), если с 5 =7, а с 7 =13 А) 2 Б) 3 В) -2 Г) другой ответ 2. Чему равна сумма первых пяти членов геометрической прогрессии (b n ), если b 1 = l, а знаменатель равен -2? А) 11 Б) -17 В) 17 Г) другой ответ 3. Найдите сумму первых пяти членов арифметической прогрессии (a n ), если a 1 =6, a 5 = - 6. А) 30 Б) 5 В) 0 Г) 1

4,6? А) n

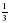
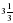
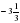
4.Чему может быть равен знаменатель геометрической прогрессии (b n ), если b 10 = l0, а b 12 = 40? А) 2 Б) ±2 В) 4 Г) 15 5.В арифметической прогрессии (с n ) разность равна -0,3, а с 1 =8. Найдите все натуральные n, при которых выполняется неравенство: с n 4,6? А) n