Тема урока "Средняя линия треугольника".
Цели урока: формирование понятия средней линии треугольника и ее свойства.
Задачи:
Образовательные:
- Ввести понятие средней линии треугольника; доказать свойство средней линии треугольника; рассмотреть свойства средней линии треугольника применительно; научить применять его при решении задач.
Развивающие:
- Развивать интерес с к геометрии, логическое мышление, интуицию учащихся; формировать умения чётко и ясно излагать свои мысли;
совершенствовать графическую культуру.
- Развивать творческую и мыслительную деятельность учащихся, их интеллектуальные качества: способность к исследовательской деятельности, к синтезу и анализу.
Воспитательные:
- Воспитывать интерес к геометрии, расширять кругозор учащихся
- Прививать аккуратность в оформлении геометрических задач, культуру устной речи.
Ход урока.
1. Вступительное слово учителя.
Эпиграфом к сегодняшнему уроку взяты слова французского писателя XIX столетия. Анатоль Франс однажды заметил: “Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом”.
Давайте последуем совету писателя и на сегодняшнем уроке: будьте активны, внимательны, поглощайте с большим желанием знания, которые пригодятся вам в дальнейшей жизни.
Тему нашего урока мы сформулируем позже, а сейчас постройте произвольный треугольник. Найдите середины боковых сторон и соедините их.
Как по вашему мнению будет называться эта линия? (средняя)
Итак, тема нашего урока «Средняя линия треугольника». Давайте сформулируем, какие цели мы должны достичь:
- Дать определение средней линии треугольника.
- Доказать теорему о средней линии треугольника.
- Доказать теорему о пересечении медиан треугольника.
2. Проверка домашнего задания.
С помощью документ камеры решение домашнего задания (№ 568 б) из тетради учащегося проектируется на экран. Учащийся комментирует решение.
3. Устная работа. Повторение изученного материала.
Цель: систематизировать базовые знания по теме «Подобие треугольников»; развивать логическое мышление; формировать умение четко и ясно излагать свои мысли.
Чтобы успешно выполнить цели сегодняшнего урока, нам не раз придется обращаться к признакам подобия треугольников. Какие признаки подобия треугольников вы знаете?
4. Понятие средней линии треугольника и ее свойства.
Цели: сформулировать определение средней линии треугольника и доказать ее свойство; развивать умение сравнивать и анализировать.
Давайте сформулируем определение средней линии.
Средняя линия треугольника это … (отрезок)
Чем являются концы этого отрезка для сторон треугольника? (середины)
Середины каких сторон треугольника соединяет этот отрезок? (боковых)
Значит средняя линия треугольника – это __что?_, который что делает? что?_ каких? сторон треугольника.
Сколько средних линий можно построить в треугольнике?
Каким же свойством обладает средняя линия треугольника?
Постройте остроугольный, прямоугольный, тупоугольный треугольники (работа в группах).
Постройте в них средние линии. Измерьте длину средней линии и основания треугольника. Сделайте вывод.
Как расположена средняя линия относительно основания треугольника?
Значит мы можем предположить, что средняя линия треугольника параллельна основанию и равна его половине. Теперь это утверждение докажем в виде теоремы.
5. Физкультминутка
6. Свойство медиан треугольника
Цель: развивать логическое мышление; способность к исследовательской деятельности, к синтезу и анализу.
Вспомните, что называется медианой треугольника? Укажите рисунок, на котором изображена медиана.
Свойство медиан треугольника: медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.
Медиану тоже считают замечательной линией треугольника. Как вы считаете, почему?
7. Закрепление нового материала. Решение задач
Цель: научить учащихся применять приобретенные на уроке знания при решении задач; развивать логическое мышление; прививать аккуратность в оформлении геометрических задач; совершенствовать графическую культуру.
№ 567
8. Подведение итогов
- Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника.
- Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
- Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины.
Оценки за урок.
9. Рефлексия учебной деятельности на уроке.
Какую цель вы ставили перед собой на уроке?
Вы достигли поставленной цели?
Что помогало выполнять задание?
Проанализируйте свою работу на уроке.
10. Домашнее задание
П. 62, вопросы 8, 9 (стр. 160). Задачи № 566, 571.
Просмотр содержимого документа
«Средняя линия треугольника»
Тема урока "Средняя линия треугольника".
Цели урока: формирование понятия средней линии треугольника и ее свойства.
Задачи:
Образовательные:
Развивающие:
совершенствовать графическую культуру.
Воспитательные:
Воспитывать интерес к геометрии, расширять кругозор учащихся
Прививать аккуратность в оформлении геометрических задач, культуру устной речи.
Ход урока.
1. Вступительное слово учителя.
Эпиграфом к сегодняшнему уроку взяты слова французского писателя XIX столетия. Анатоль Франс однажды заметил: “Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом”.
Давайте последуем совету писателя и на сегодняшнем уроке: будьте активны, внимательны, поглощайте с большим желанием знания, которые пригодятся вам в дальнейшей жизни.
Тему нашего урока мы сформулируем позже, а сейчас постройте произвольный треугольник. Найдите середины боковых сторон и соедините их.
Как по вашему мнению будет называться эта линия? (средняя)
Итак, тема нашего урока «Средняя линия треугольника». Давайте сформулируем, какие цели мы должны достичь:
2. Проверка домашнего задания.
С помощью документ камеры решение домашнего задания (№ 568 б) из тетради учащегося проектируется на экран. Учащийся комментирует решение.
3. Устная работа. Повторение изученного материала.
Цель: систематизировать базовые знания по теме «Подобие треугольников»; развивать логическое мышление; формировать умение четко и ясно излагать свои мысли.
Чтобы успешно выполнить цели сегодняшнего урока, нам не раз придется обращаться к признакам подобия треугольников. Какие признаки подобия треугольников вы знаете?
4. Понятие средней линии треугольника и ее свойства.
Цели: сформулировать определение средней линии треугольника и доказать ее свойство; развивать умение сравнивать и анализировать.
Давайте сформулируем определение средней линии.
Средняя линия треугольника это … (отрезок)
Чем являются концы этого отрезка для сторон треугольника? (середины)
Середины каких сторон треугольника соединяет этот отрезок? (боковых)
Значит средняя линия треугольника – это __что?_, который что делает? что?_ каких? сторон треугольника.
Сколько средних линий можно построить в треугольнике?
Каким же свойством обладает средняя линия треугольника?
Постройте остроугольный, прямоугольный, тупоугольный треугольники (работа в группах).
Постройте в них средние линии. Измерьте длину средней линии и основания треугольника. Сделайте вывод.
Как расположена средняя линия относительно основания треугольника?
Значит мы можем предположить, что средняя линия треугольника параллельна основанию и равна его половине. Теперь это утверждение докажем в виде теоремы.
5. Физкультминутка
6. Свойство медиан треугольника
Цель: развивать логическое мышление; способность к исследовательской деятельности, к синтезу и анализу.
Вспомните, что называется медианой треугольника? Укажите рисунок, на котором изображена медиана.
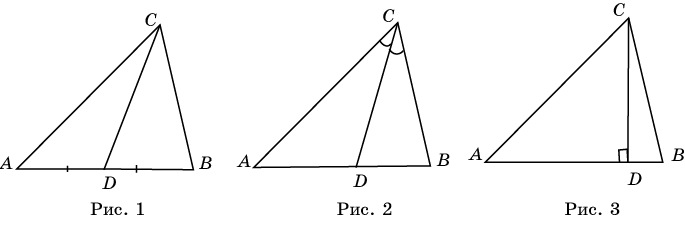
Свойство медиан треугольника: медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.
Медиану тоже считают замечательной линией треугольника. Как вы считаете, почему?
7. Закрепление нового материала. Решение задач
Цель: научить учащихся применять приобретенные на уроке знания при решении задач; развивать логическое мышление; прививать аккуратность в оформлении геометрических задач; совершенствовать графическую культуру.
№ 567
8. Подведение итогов
Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника.
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины.
Оценки за урок.
9. Рефлексия учебной деятельности на уроке.
Какую цель вы ставили перед собой на уроке?
Вы достигли поставленной цели?
Что помогало выполнять задание?
Проанализируйте свою работу на уроке.
10. Домашнее задание
П. 62, вопросы 8, 9 (стр. 160). Задачи № 566, 571.
Просмотр содержимого презентации
«Средняя линия треугольника»

СРЕДНЯЯ ЛИНИЯ ТРЕУГОЛЬНИКА

Актуализация знаний
8
10
5
CD = , AD = , CE = , ВE = Доказать: а) CDE CAB;
б) AB II DE.
10
5
8
4
C
1
D
E
Доказательство.
а)
2
A
B
CAB (по II признаку )
CDE
AB II DE
б)
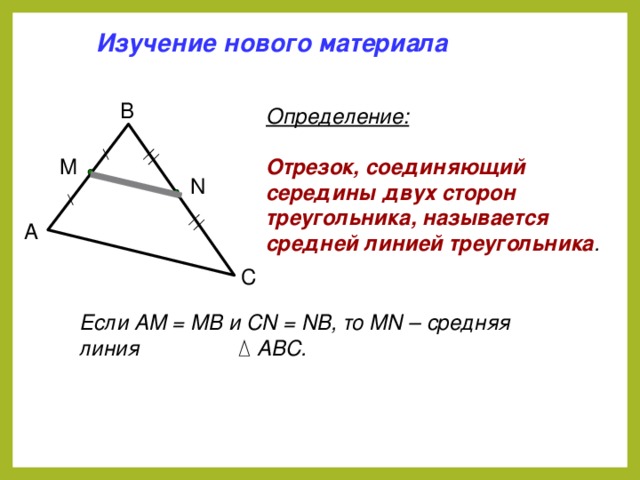
Изучение нового материала
B
Определение:
Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника .
M
N
A
C
Если АМ = МВ и СN = NB, то MN – средняя линия
АВС.
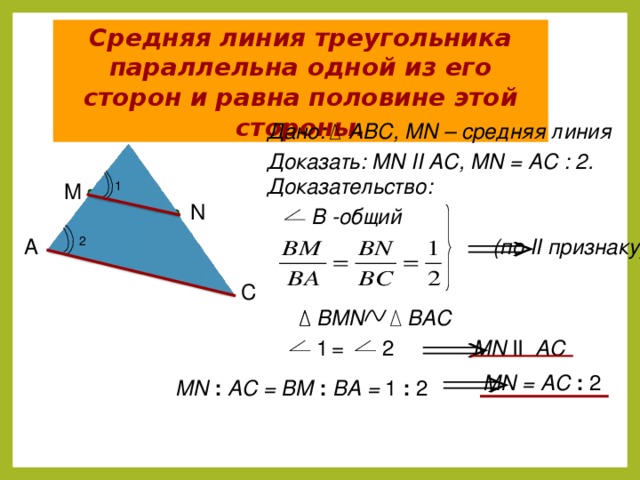
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Дано: АВС, MN – средняя линия
B
Доказать: MN II AC, MN = АC : 2.
Доказательство:
M
1
N
В -общий
(по II признаку)
2
А
C
BAC
BMN
MN II AC
=
1
2
MN = AC : 2
MN : AC = BM : BA = 1 : 2
4
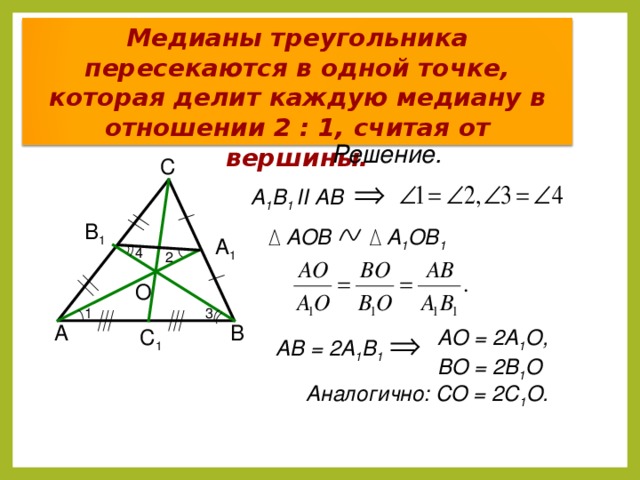
Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины.
Решение.
С
А 1 В 1 II АВ
В 1
АОВ
А 1 ОВ 1
А 1
4
2
О
1
3
А
В
АО = 2А 1 О, ВО = 2В 1 О
С 1
АВ = 2А 1 В 1
Аналогично: СО = 2С 1 О.
5
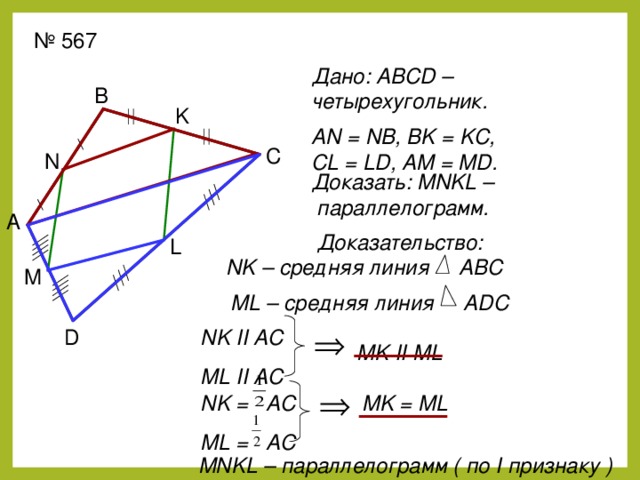
№ 567
Дано: ABCD – четырехугольник.
В
K
AN = NB, BK = KC,
CL = LD, AM = MD.
С
N
Доказать: MNKL –
параллелограмм.
А
Доказательство:
L
NK – средняя линия ABC
M
ML – средняя линия ADC
NK II AC
ML II AC
D
MK II ML
MK = ML
NK = AC
ML = AC
MNKL – параллелограмм ( по I признаку )
А
В
С
А 1
В 1
С 1
О
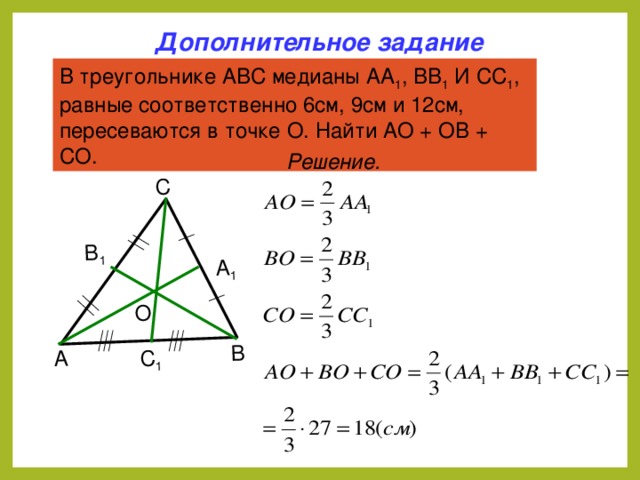
Дополнительное задание
В треугольнике АВС медианы АА 1 , ВВ 1 И СС 1 , равные соответственно 6см, 9см и 12см, пересеваются в точке О. Найти АО + ОВ + СО.
Решение.
5

Итог урока
Отрезок , соединяющий середины двух сторон треугольника, называется средней линией треугольника .
1.
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
2.
Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины.
3.
5

Домашнее задание
П. 62, вопросы 8, 9
Задачи № 566, 571
5


























