Урок математики в 11 классе "Степень"

Обобщающий урок по теме: «Степень.» 11-й класс

Тип урока: Обобщение и систематизация.

Цели урока:

• Образовательная

  • систематизировать знания учащихся по пройденной теме;

  • проверить уровень изученного материала;

  • применить теоретический материал для решения задач.

• Воспитательная

  • воспитывать чувство ответственности за выполненную работу;

  • воспитывать культуру речи, аккуратность, внимание.

• Развивающая

  • развивать мыслительную деятельность учащихся;

  • прививать интерес к предмету.

Ход урока

1. Оргмомент.

Перед вашими глазами высказывание английского математика Джеймса Джозефа Сильвестра (1814–1897) “Математика – это музыка разума”.

“Музыка – это математика чувств”.

К чувствам мы можем отнести различного рода переживания. В этом году одной из причин ваших и моих переживаний является успешная сдача ЕГЭ и, как следствие, поступление в ВУЗ. Очень хочется, чтобы преобладали положительные эмоции. Должна быть уверенность, а это наши знания и навыки. Сегодня на уроке мы повторим определения и формулы по теме «Степень»; рассмотрим преобразование выражений, содержащих степени и решение иррациональных уравнений.

2.Актуализация опорных знаний.

(2 человека у доски дописывают основные свойства корней и степеней)

Повторим теорию.

1) Дайте определение корня n-ой степени из числа.

(Корнем n-ой степени из числа a называется такое число х, n-я степень которого равна a.)

2) Что такое арифметический корень n –ой степени?

(Арифметическим корнем n-ой степени из числа а называют такое неотрицательное число b, n-ая степень которого равна а.)

3) Найдите значение выражения

4) Сформулируйте основные свойства корней.

• корень из произведения неотрицательных множителей равен произведению корней из этих множителей.

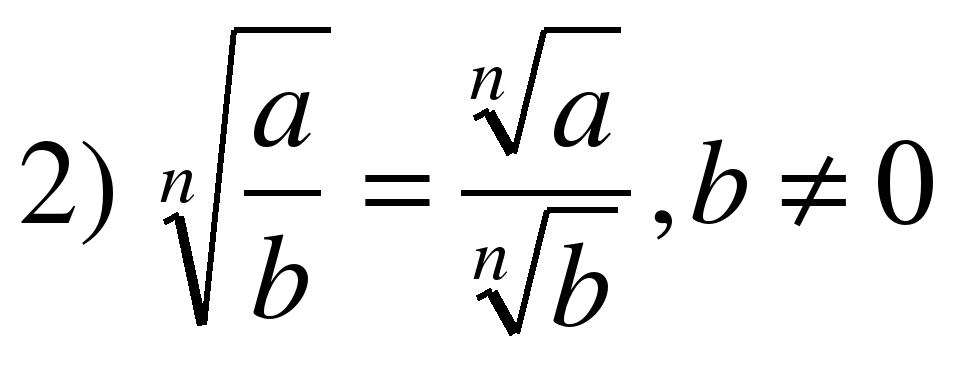• корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, деленному на корень из знаменателя.

• Извлечение корня из корня

• показатель степени подкоренного выражения можно вынести за знак корня

• Показатель корня и показатель степени подкоренного выражения можно разделить на одно и то же натуральное число.

Вопрос:

Как можно записать степень с рациональным показателем в виде выражения, содержащего корень

5) сформулируйте основные свойства степеней

Для любых а 0, b0 и любых рациональных r и s :

В картах самоконтроля(записать только ответ)

1) Найдите значение выражения:

  

В картах самоконтроля(записать только ответ)

2) Представьте степень с дробным показателем в виде корня:

1)_= 2)- 8^1,5= 3)_ 4) _=

Дополнительно

Решите уравнение х³=125 х⁴=64 х⁵=-_ х⁴=-16

Повторим теорию

6) Какие уравнения называются иррациональными?

(Уравнение, в котором под знака радикала содержится переменная, называется иррациональным)

В картах самоконтроля(записать только ответ)

3) Из предложенных уравнений запишите номера тех, которые являются иррациональными:

_{ }

2) 2х²-5х+9=0 7) 2сos х-1=0

_ 8)_=_

4)у²-3_ у=4 9)х_=1+х

5)7х-8=11

№1,3,6,8

Повторим теорию

7)Какими основными способами решаются иррациональные уравнения?

• возведения в степень, равную показателю корня

• введения новой переменной

Расскажите алгоритм решения иррационального уравнения.

1) Возвести обе части уравнения в степень, равную показателю корня.

2) Решить полученное уравнение.

3) Сделать проверку.

Всегда ли нужно делать проверку? (нет, при возведении в нечетную степень посторонние корни не появляются)

В картах самоконтроля(записать только ответ)

4)Решите уравнение:

Подведите итог по баллам.

Физминутка для глаз.

3. Формирование навыков.

Работа проводится по двум направлениям в зависимости от уровня ЗУН.

1 направление. (Те учащиеся, которые хорошо владеют навыками применения свойств, решают самостоятельно упражнения.)

1) Найдите значение числового выражения

А) _ =15

Б) _ 6 15/16

2) Упростите выражение

_ =4аb²c³

2) Решите уравнение

_-9+х=0 х=12-пост , х=7

Х-1= х=2

2 направление.

Остальные учащиеся работают с учителем у доски. Выполнение упражнений:

1) Упростить выражение

_ =15 _ =7 _ =1,5 _ =9

2) Решить уравнение

Х=31 х=35 х=-8,х=-9

4. Домашнее задание.(дифференцированное)

1) стр 273 №2,3(2), №13(2а,б) (на «3») преобразование выражений, иррациональные уравнения

2) №439,440,стр223, №147(а,б)стр 297(на «4и5»)

.

5. Проверка ЗУН. Проверочная работа из заданий ЕГЭ.

В то время, пока учащиеся выполняют проверочную работу, учитель проверяет работы сильных учеников и выставляет оценки.

6. Подведение итогов.

Сообщаются оценки, полученные на этом уроке. Ответить на вопросы: Чем занимались на уроке? Для чего? В конце листа самоконтроля нарисуйте смайлик.

Карта самоконтроля ученика…………………………………………………………………………………..

Для сильных учеников

Английский математик

Джеймс Джозеф Сильвестр

1814 - 1897

11 класс

Повторяем теорию

• Дайте определение корня n-ой степени из числа.
• Что такое арифметический корень n-ой степени?

Найдите значение выражения

В картах самоконтроля

• Выполните задания № 1 и №2

В картах самоконтроля:

• 1) Найдите значение выражения:

• В картах самоконтроля: 2) Представьте степень с дробным показателем в виде корня:

1.

2.

не имеет смысла

3.

4.

Повторяем теорию

• Какие уравнения называются иррациональными?
• Уравнение, в котором под знака радикала содержится переменная, называется иррациональным

В картах самоконтроля: 3) Из предложенных уравнений запишите номера тех, которые являются иррациональными:

• 1)
• 2)
• 3)
• 4)
• 5) 7х-8=11

• 6)
• 7) 2cosх – 1=0
• 8)
• 9)

Повторяем теорию

• 7) Какими основными способами решаются иррациональные уравнения?
• - возведения в степень, равную показателю корня
• - введения новой переменной
• 8) Расскажите алгоритм решения иррационального уравнения
• 9)Всегда ли нужна проверка?

В картах самоконтроля: Решите уравнения

Работа в тетрадях Найти значение выражения

Решите уравнение

Домашнее задание:

• 1) стр 273
• № 2,3(2), №13(2а,б)
• 2) стр223
• № 439,440,
• стр 297 №147(а,б)

В картах самоконтроля: Проверочная работа

отличное

плохое

равнодушное

Покажите ту, которая соответствует настроению в данный момент.

Спасибо за урок!

Обобщение понятия степени