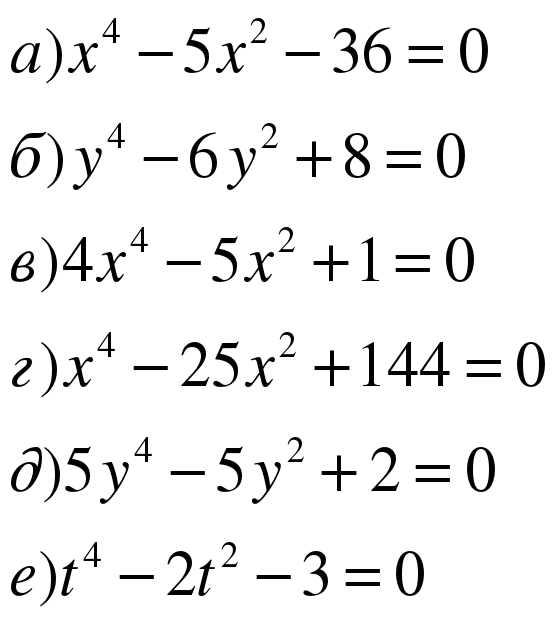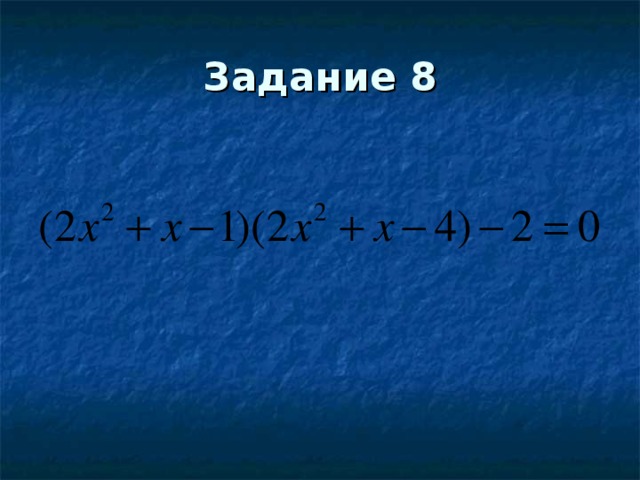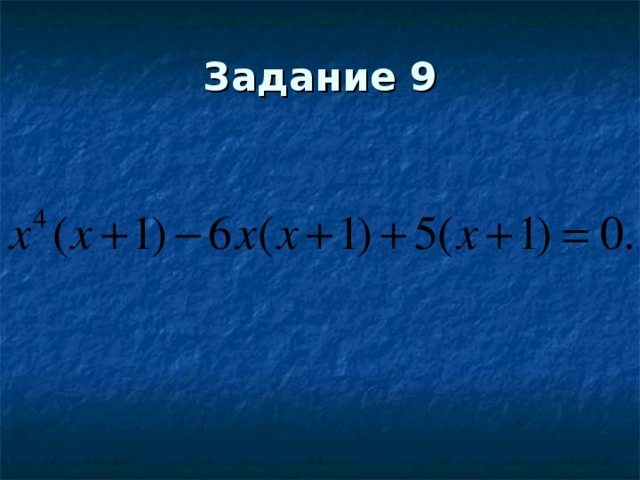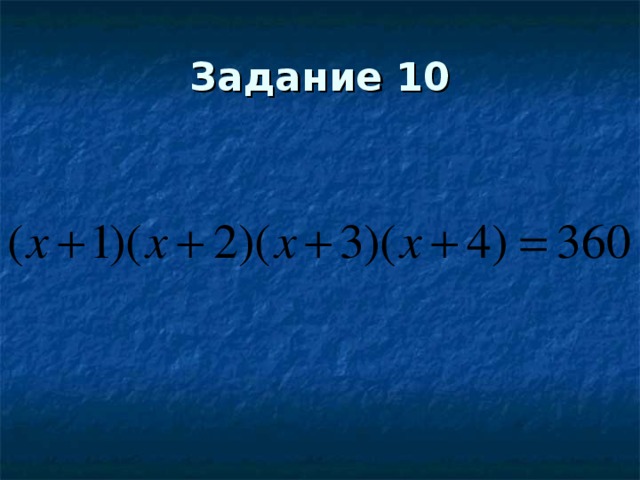Автор: Сватковская Елена Александровна,
учитель математики,
МБНОУ «Лицей № 3 (искусств)»
УРАВНЕНИЯ, ПРИВОДИМЫЕ К КВАДРАТНЫМ.
БИКВАДРАТНЫЕ УРАВНЕНИЯ. (СЛАЙД 1)
Предварительная подготовка к уроку: учащиеся должны уметь решать биквадратные уравнения и уравнения, приводимые к квадратным, владеть методом введения новой переменной; учащиеся заранее готовят сообщения о великих итальянских ученых-математиках.
Цели урока:
а) образовательная: рассмотрение способов решения уравнений, приводимых к квадратным уравнениям;
б) воспитательная: воспитание навыков групповой работы, сознательной деятельности учащихся;
в) развивающая: развитие мыслительной деятельности учащихся, навыков взаимодействия между учащимися, умения обобщать изучаемые факты.
Оборудование: сетка кроссворда на карточках, карточки, плакат-план путешествия, записи на доске, диапроектор, компьютер, копирка.
Тип урока: урок-путешествие по стране «Математика».
ХОД УРОКА:
Организационный момент
(План путешествия, в котором перечислены названия станций, записан на доске или плакате.)
Сегодня мы отправимся в путешествие по стране «Математика». Остановимся в городе Уравнений третьей и четвертой степени, продолжим знакомство с биквадратными уравнениями, услышим новое о математиках.
Путешествие по стране «Математика»
СТАНЦИЯ ЛЮБИТЕЛЕЙ КРОССВОРДОВ
У каждого из вас есть карточки с сеткой кроссворда и вопросами. Под карточку положите чистый лист и копирку. Ответы записывайте только в именительном падеже. Разгадайте кроссворд, сдайте карточки, а по листу проведите самопроверку. (СЛАЙД 2)
По горизонтали:
4.Чем является выражение 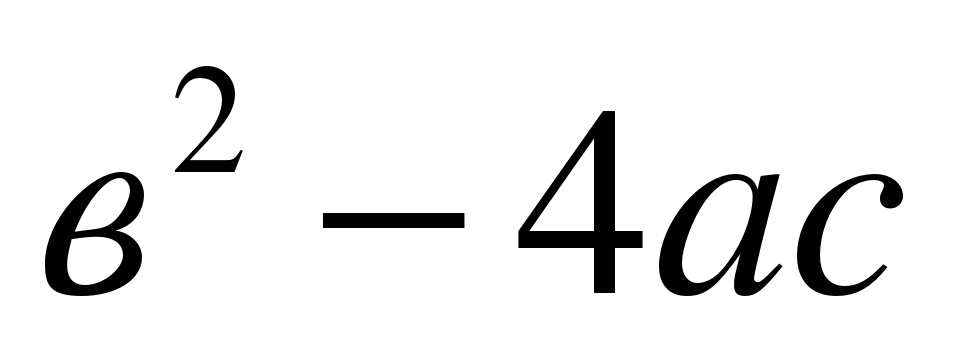 для квадратного уравнения? (дискриминант)
для квадратного уравнения? (дискриминант)
6.Значение переменной, при которой уравнение обращается в верное равенство. (корень)
8.Уравнение вида  , где
, где  . (биквадратное)
. (биквадратное)
9.Французский математик, имеющий отношение к квадратным уравнениям. (Виет)
10.Уравнение, в котором левая и правая части являются целыми выражениями. (целое)
11. Уравнения с одной переменной, имеющие одинаковое множество корней. (равносильные)
По вертикали:
1.Множество корней уравнения. (решение)
2.Решение уравнения 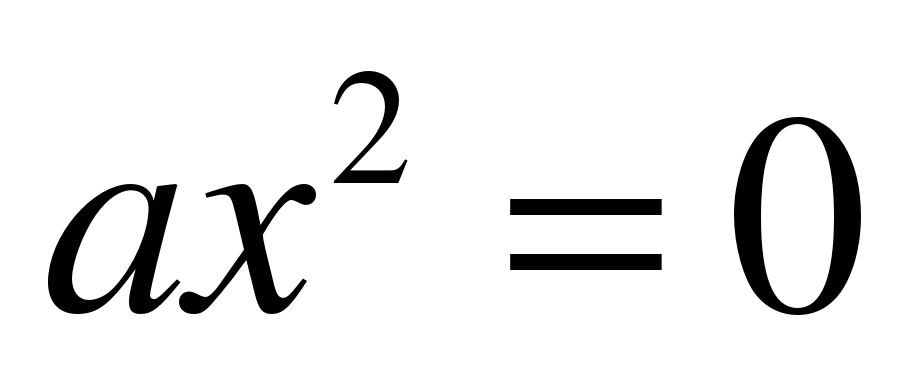 . (ноль)
. (ноль)
3.Равенство, содержащее переменную. (уравнение)
5.Квадратное уравнение, в котором один из коэффициентов b или с равен 0. (неполное)
7. Квадратное уравнение, в котором первый коэффициент равен единице. (приведенное)
СТАНЦИЯ «ИСТОРИЧЕСКАЯ»
Ученик: В проблему уравнений 3-й и 4-й степеней большой вклад внесли итальянские математики 16 века Н.Тарталья, А.Фиоре, Д.Кардано и др. В 1535 г. между А.Фиоре и Н.Тартальей состоялся научный поединок, на котором последний одержал победу. Он за 2 часа решил 30 задач, предложенных Фиоре, а сам Фиоре не смог решить ни одной, заданной ему Тартальей.
Учитель: Кто еще подготовил сообщения? (заслушиваются сообщения, подготовленные учащимися. На каждое 2-3 минуты.)
ГОРОД УРАВНЕНИЙ (устная часть)
Это не просто город Уравнений, а уравнений 3-й и 4-й степеней. Вам предстоит ответить на все вопросы. Только ответив на них, вы сможете отправиться дальше.
ЗАДАНИЕ 1. Каким способом вы решали бы уравнения каждой из групп?
(Уравнения к заданиям 1-3 высвечиваются на экран) (СЛАЙД 3)
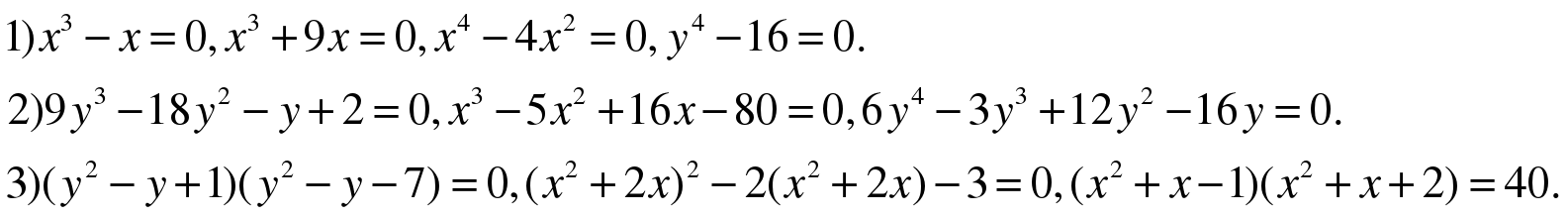
ОТВЕТЫ: Примеры группы 1) лучше решать разложением на множители с помощью вынесения общего множителя за скобки или с помощью формул сокращенного умножения.
Примеры группы 2) лучше решать способом группировки и разложения на множители.
Примеры группы 3) лучше решать введением новой переменной и переходом к квадратному уравнению.
ЗАДАНИЕ 2. Какой множитель вы вынесли бы за скобки в примерах группы 1) задания 1? (СЛАЙД 3)
ОТВЕТЫ: 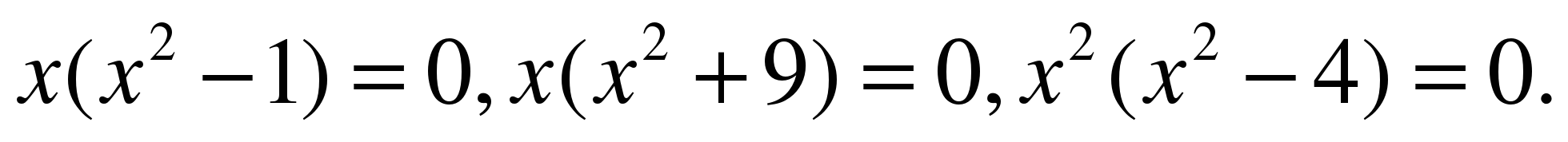
ЗАДАНИЕ 3. Как вы сгруппировали бы слагаемые в примерах группы 2) задания 1? (СЛАЙД 3)
ОТВЕТЫ: 
ЗАДАНИЕ 4. Что бы вы обозначили через новую переменную в примерах группы 3) задания 1? (СЛАЙД 3)
ОТВЕТЫ: 
ЗАДАНИЕ 5. Как можно разложить на множители многочлен 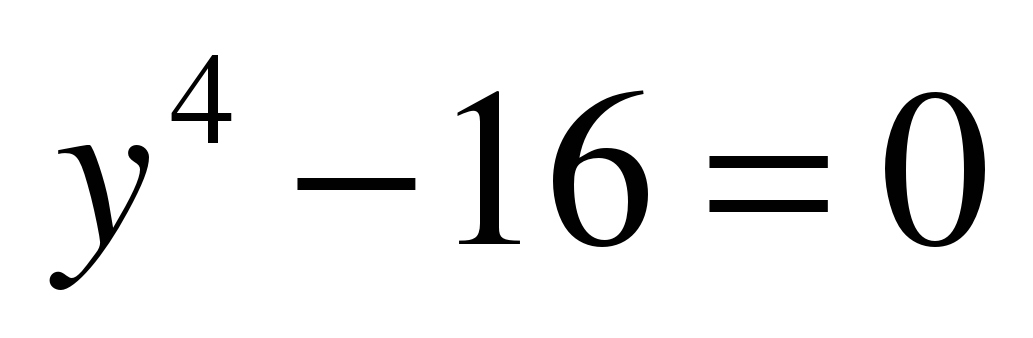 ?
?
ОТВЕТЫ: 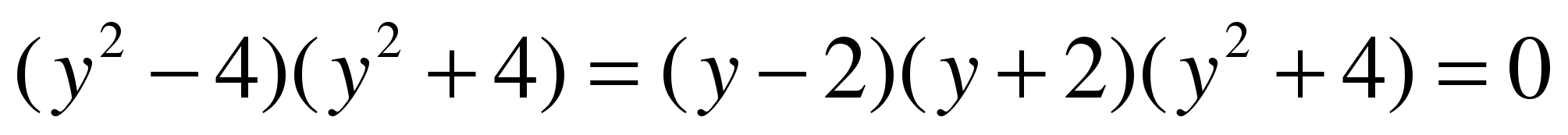 .
.
ГОРОД УРАВНЕНИЙ (практическая часть)
Вы справились с устной работой, и мы отправляемся дальше.
ЗАДАНИЕ 6. Решите уравнение. (См. приложение.)
(задание у доски одновременно решают 2 ученика.)
а) (Первый ученик решает у доски с объяснением.) 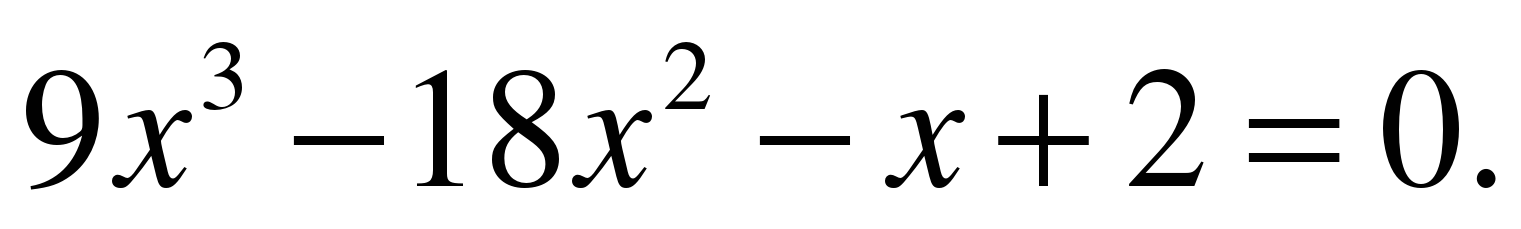
б) (Второй учащийся решает уравнение молча, затем объясняет решение, класс слушает и задает вопросы, если что-то непонятно.) 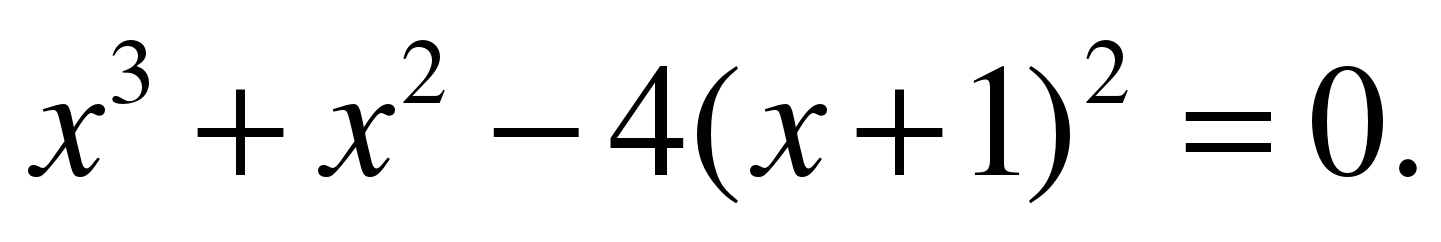
ЗАДАНИЕ 7. Решите уравнение. (См. приложение.)
(Задание выполняется самостоятельно по вариантам, предварительно оговорив замену для введения новой переменной. Проверяется устно.) (СЛАЙД 4)
Вариант 1 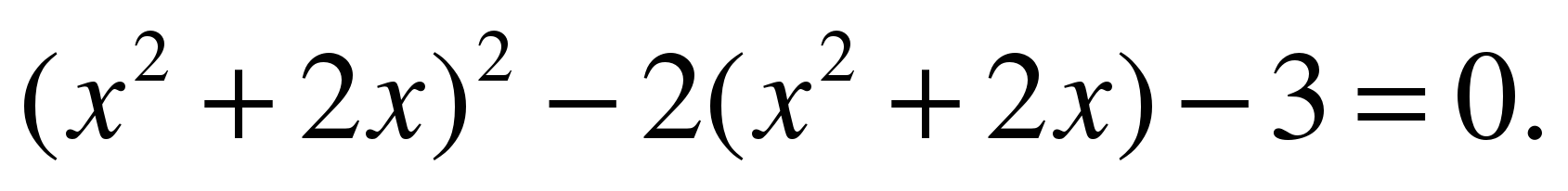 Замена:
Замена: 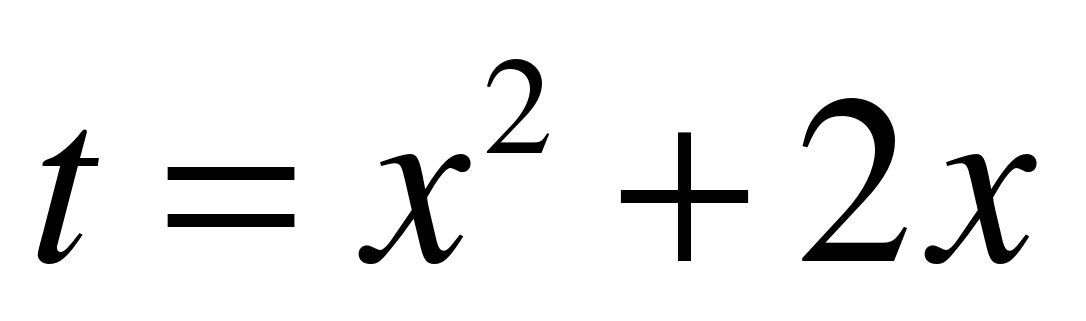 .
.
Вариант 2 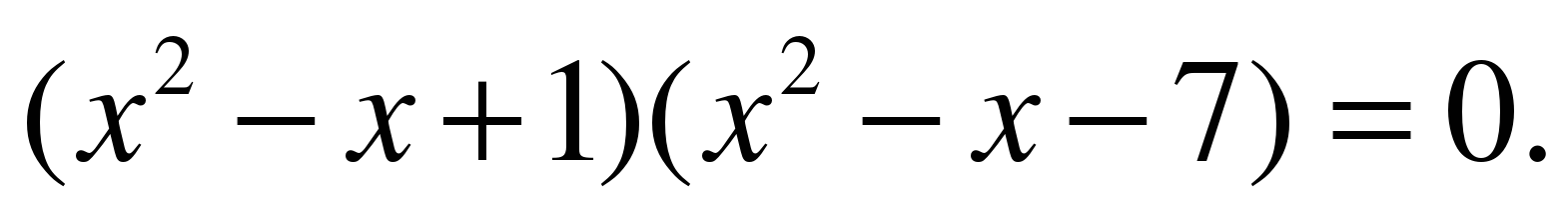 Замена:
Замена: 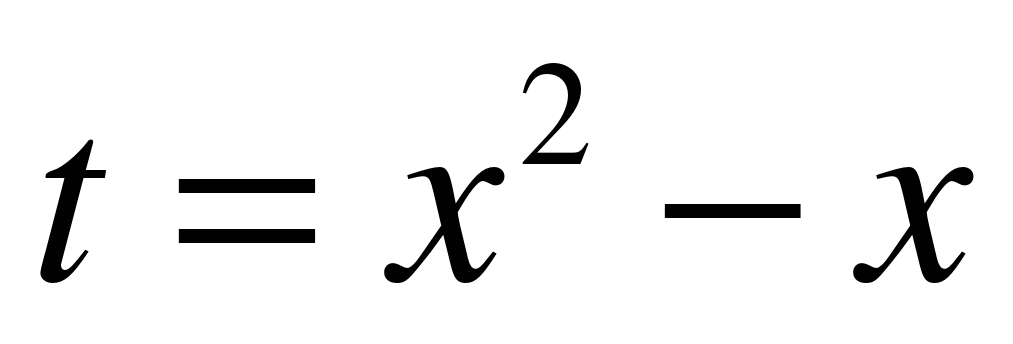 .
.
ЗАДАНИЕ 8. Решите уравнение. (См. приложение.)
(Дополнительно для тех, кто раньше справился с предыдущими уравнениями).
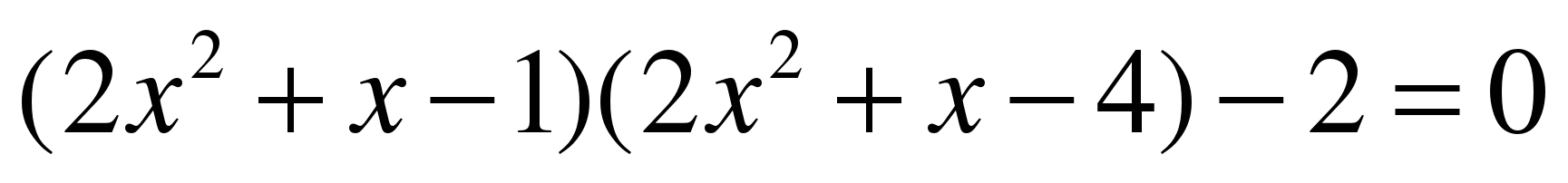 . (СЛАЙД 5)
. (СЛАЙД 5)
ЗАДАНИЕ 9. Решите уравнение. (СЛАЙД 6)
(Ход решения учащимися комментируется с места.) 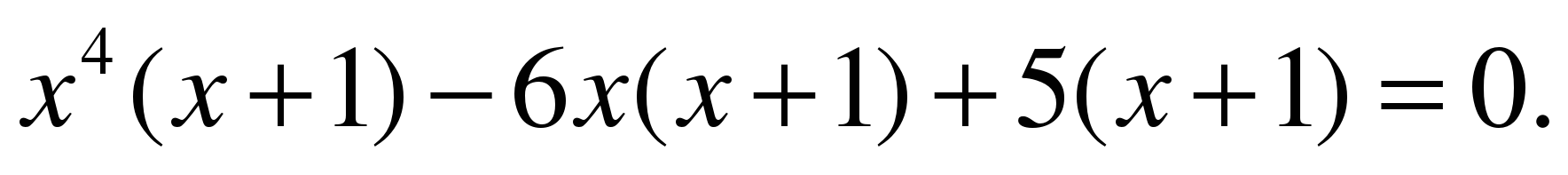
РЕШЕНИЕ: Вынесем общий множитель:  ,
,
откуда 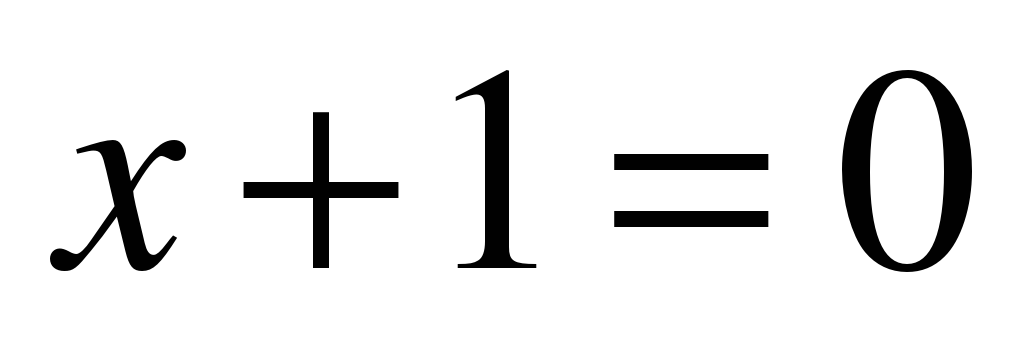 или
или 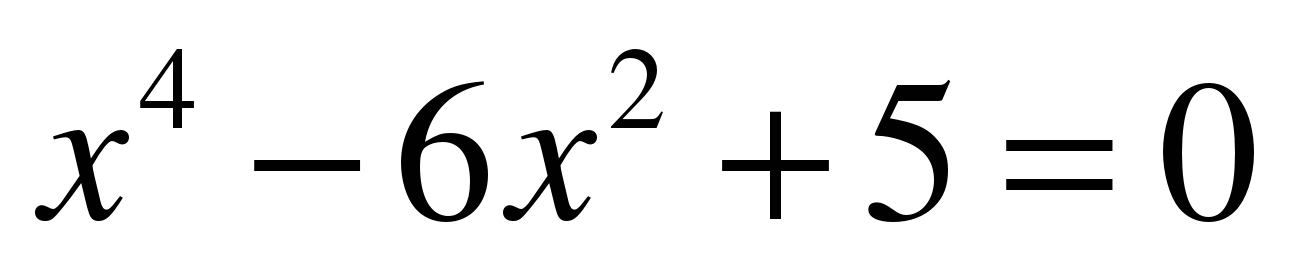 , т.е.
, т.е.
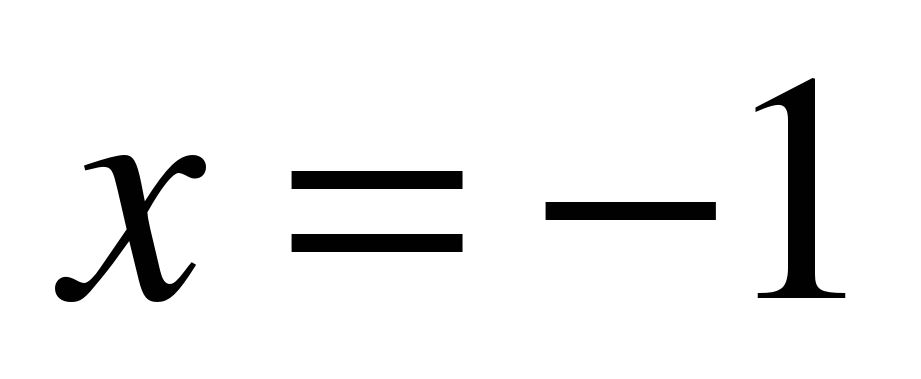


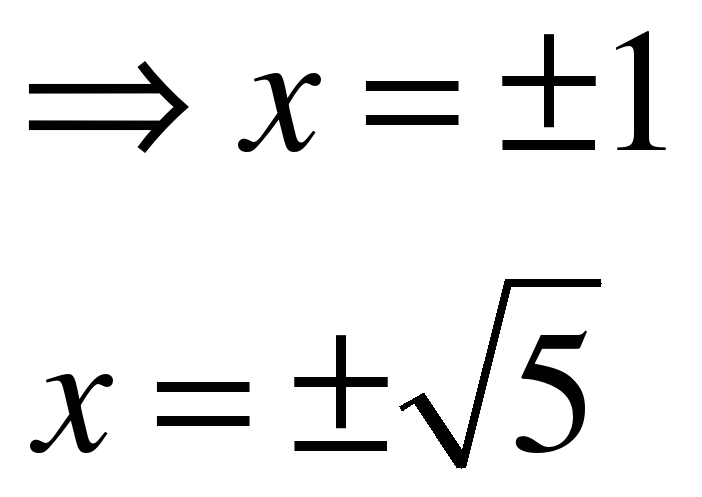
ОТВЕТ: 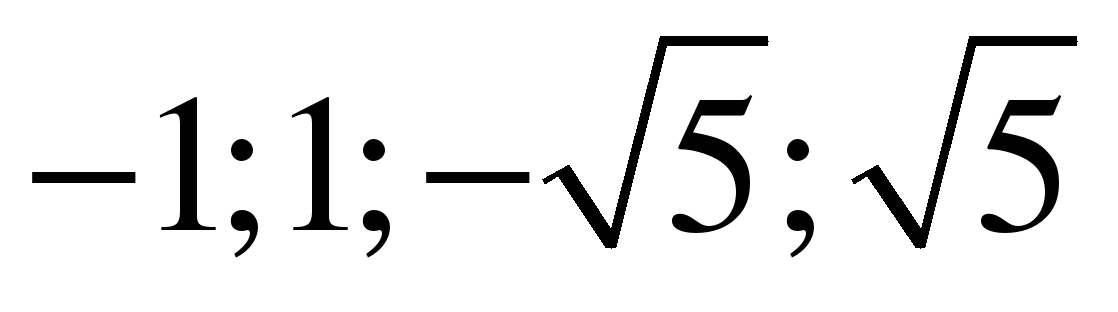
ЗАДАНИЕ 10. Решите уравнение.
(Предварительно учитель обсуждает с классом способ решения. Затем учащийся решает часть примера у доски.) (СЛАЙД 7)
 .
.
РЕШЕНИЕ: Сначала сгруппируем множители:
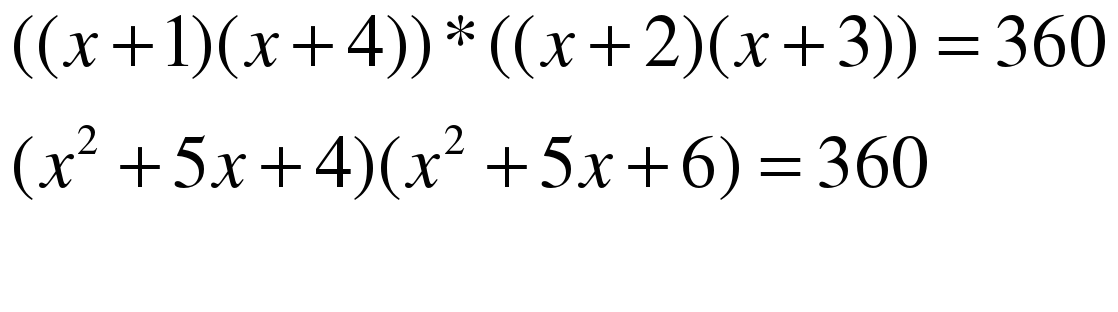 Замена:
Замена: 
(Далее уравнение решается самостоятельно с дальнейшей устной проверкой.)

Значит,  или
или 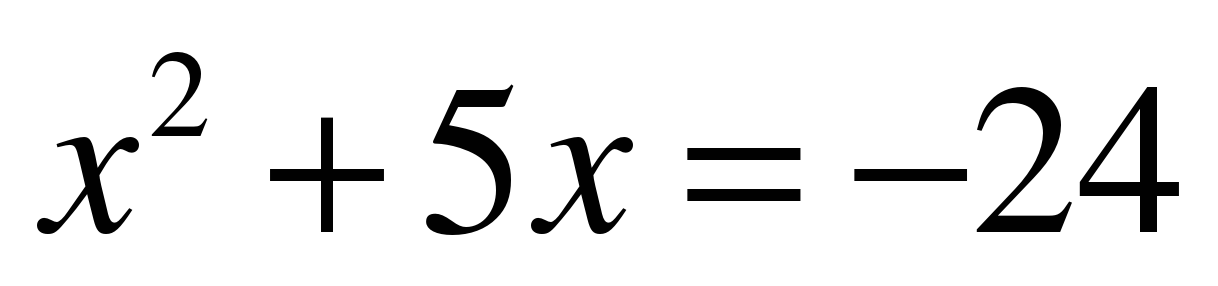 (Второе уравнение корней не имеет, т.к. дискриминант меньше нуля)
(Второе уравнение корней не имеет, т.к. дискриминант меньше нуля)
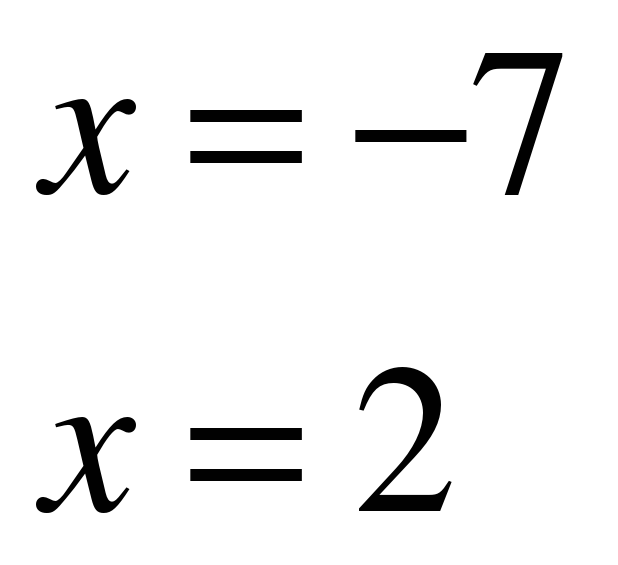
ОТВЕТ: -7; 2.
ЗАДАНИЕ 11. Решите уравнение. (См. приложение.)
(Тот, кто верно решит больше биквадратных уравнений за 10 минут, получит «5». Учащиеся работают самостоятельно с последующей взаимопроверкой). (СЛАЙД 8)
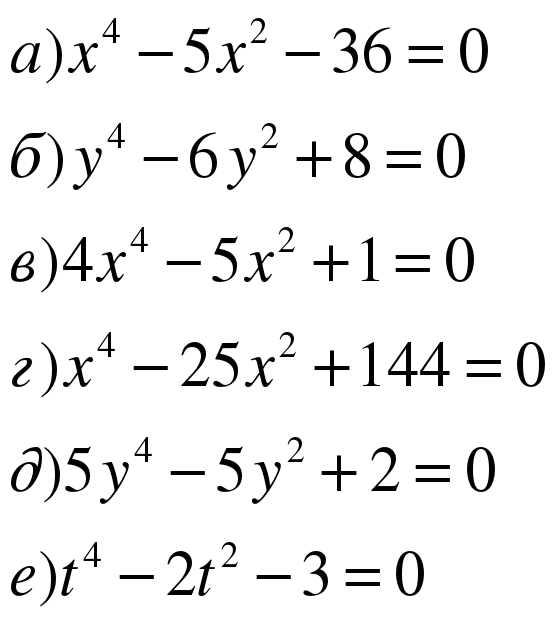
ЗАДАНИЕ 12. При каких значениях а уравнение 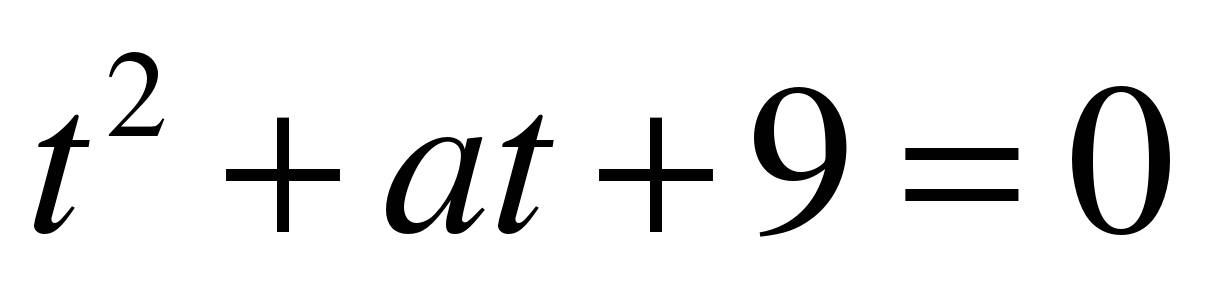 не имеет корней? (См. приложение.) (СЛАЙД 9)
не имеет корней? (См. приложение.) (СЛАЙД 9)
(Пример на повторение.)
СТАНЦИЯ «ДОМАШНЯЯ»
Вы прибыли на станцию «Домашняя». Получите домашнее задание:
ЗАДАНИЕ 13. Решите уравнение итальянских математиков
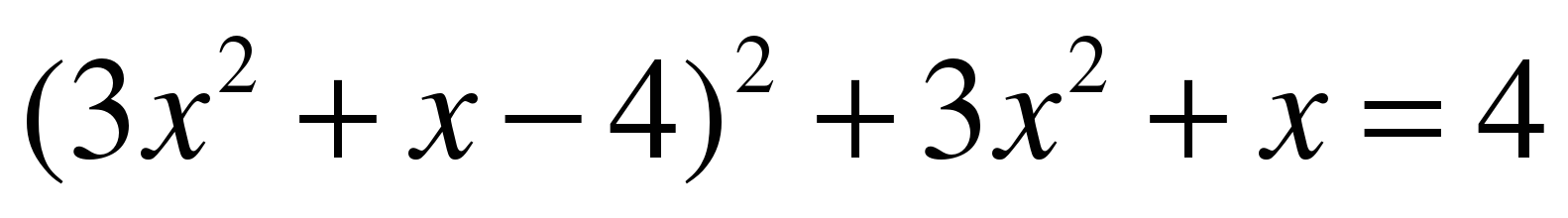 . (См. приложение.) (СЛАЙД 10)
. (См. приложение.) (СЛАЙД 10)
ЗАДАНИЕ 14. Найдите и решите 3-4 уравнения, предложенные А.Фиоре и Н.Тартальей.
Подведение итогов урока.
Наше путешествие завершено. Итак, подсчитайте, сколько каждый из вас решил уравнений.
За урок весь класс решил…..уравнений. Оценки за урок….
ЛИТЕРАТУРА:
Алгебра: Сборник заданий для проведения письменного экзамена по алгебре за курс основной школы. 9 класс. – М.: Дрофа, 1996
Алимов Ш.А., Колягин Ю.М. Алгебра: Учебник для 9 класса общеобразовательных учреждений. – М.: Просвещение, 2007
Нагибин Ф.Ф., Канн, Канин Е.С. Математическая шкатулка. – М.: Просвещение, 1988
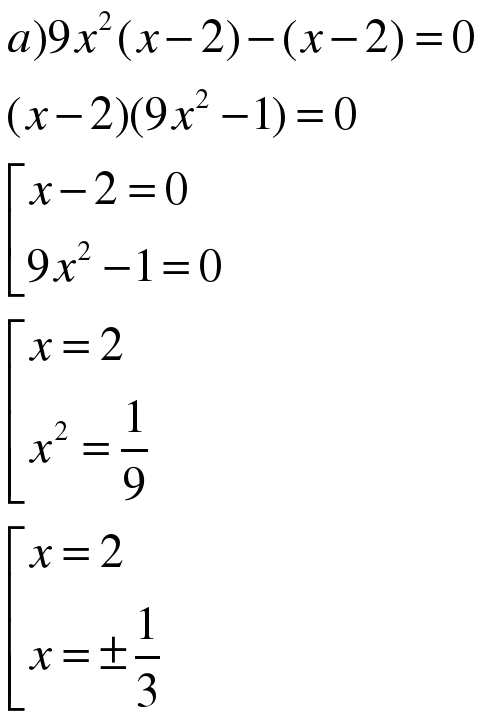
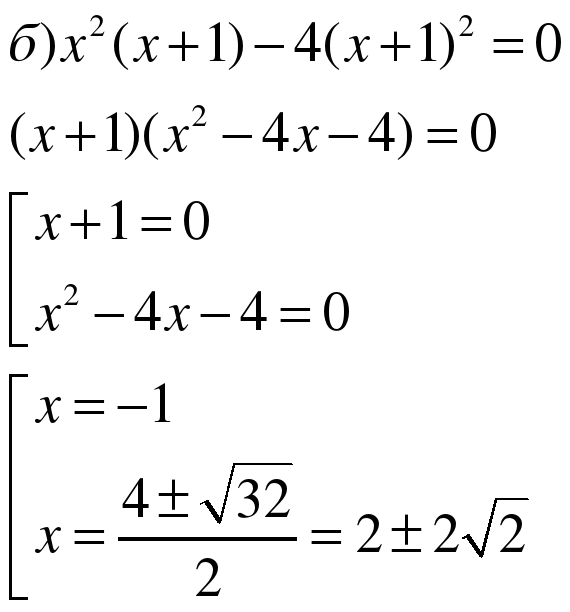
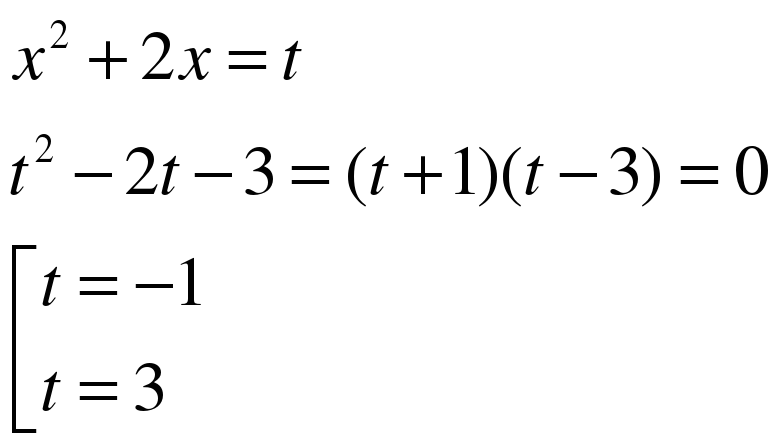
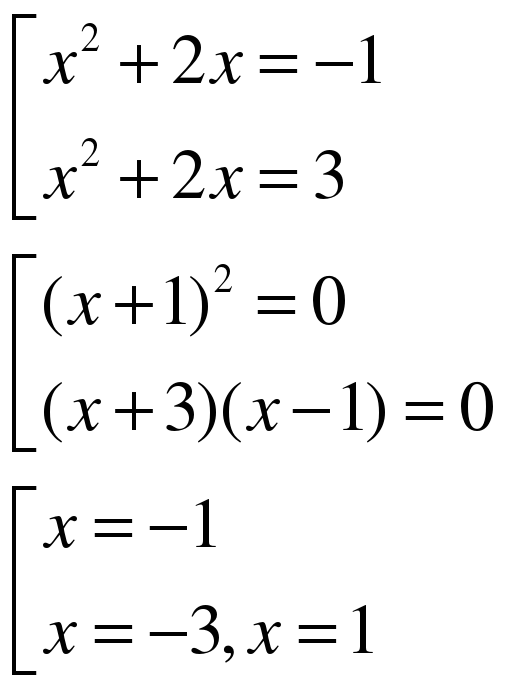
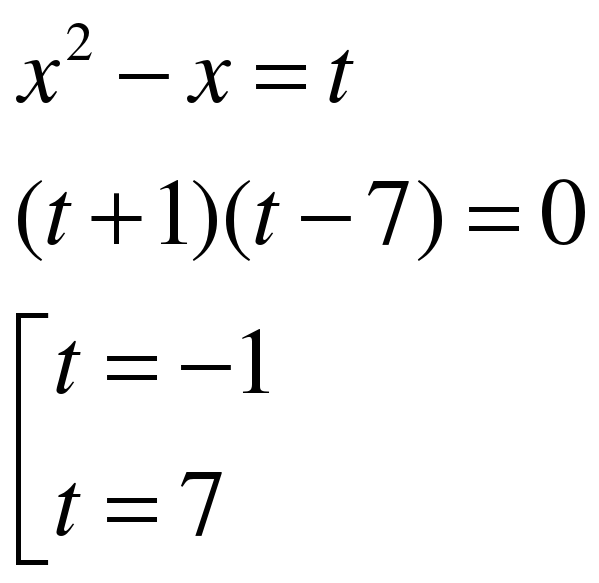
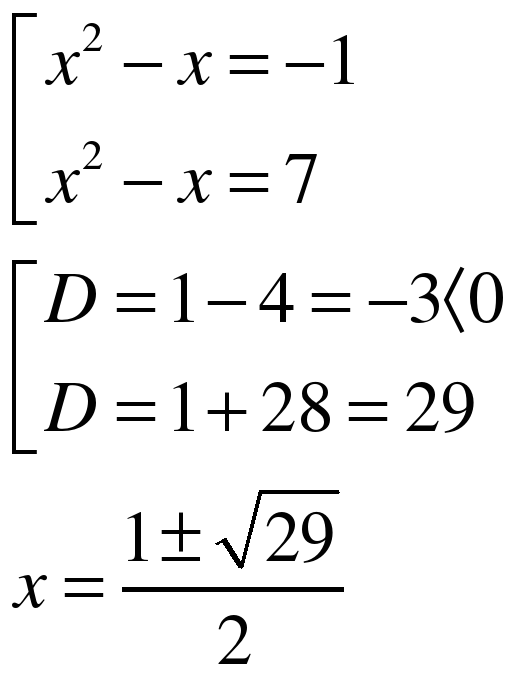
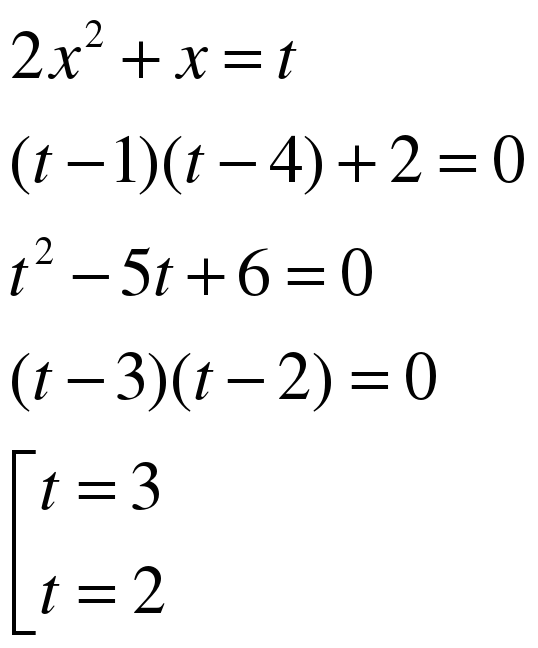


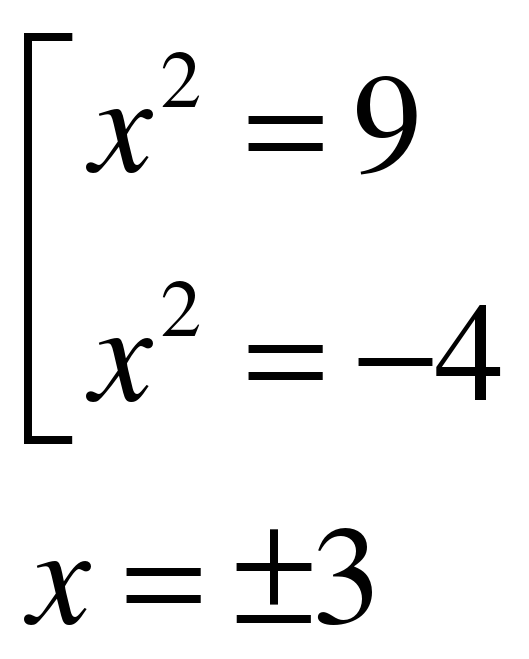
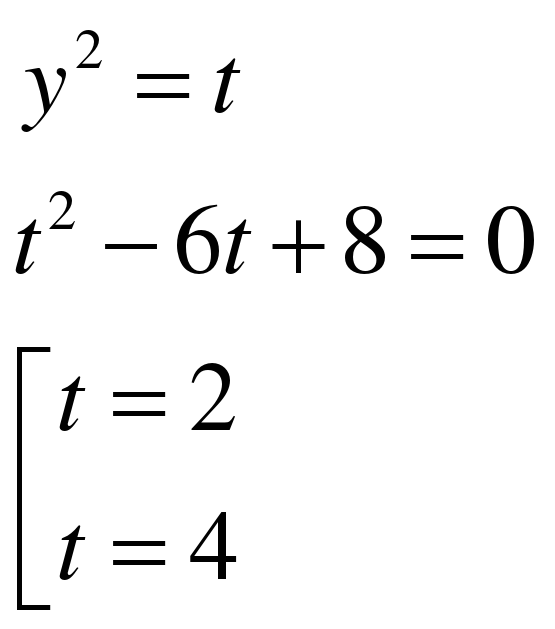
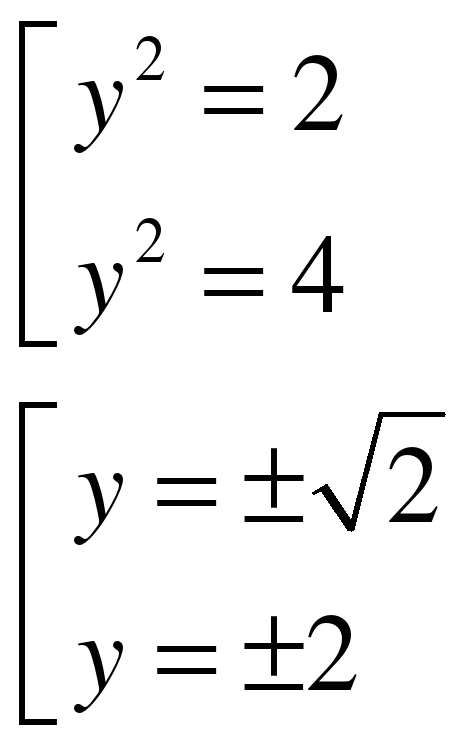
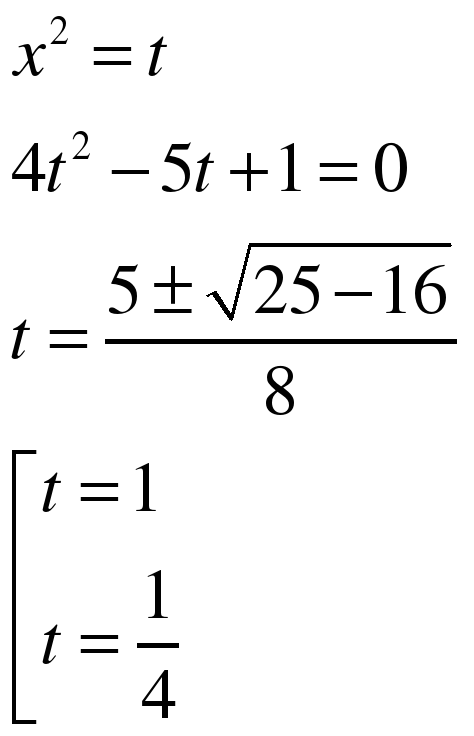

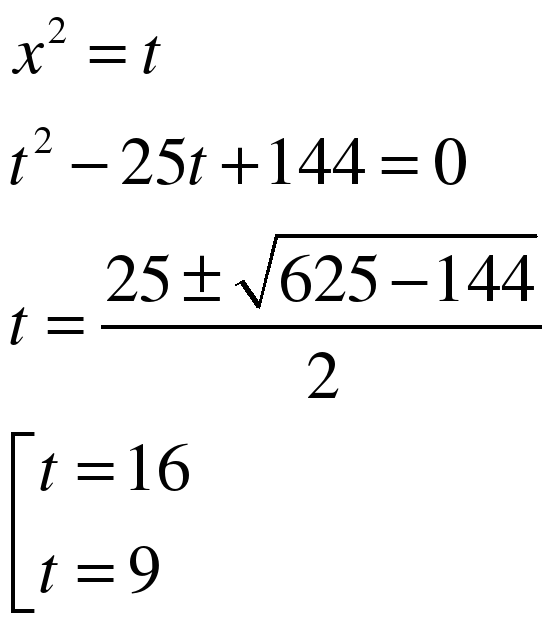
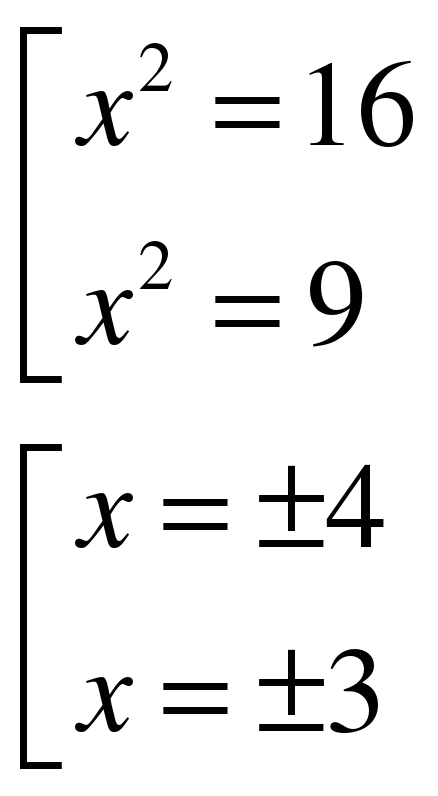
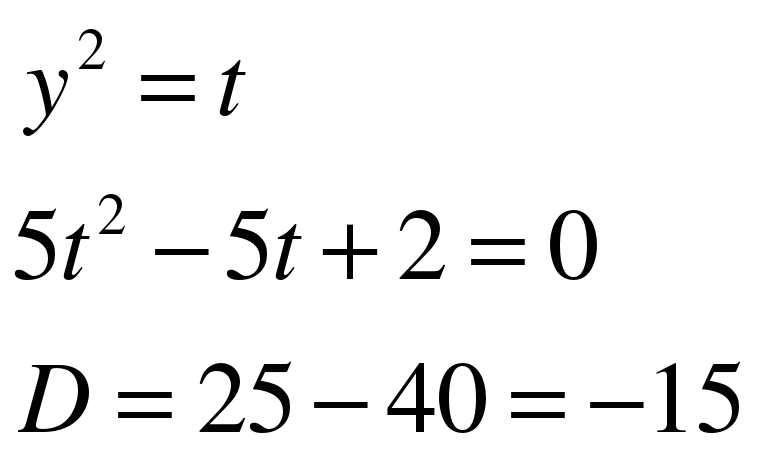


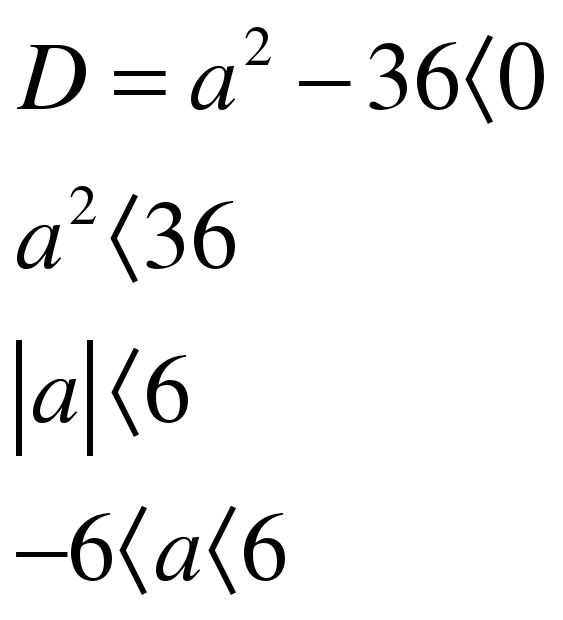
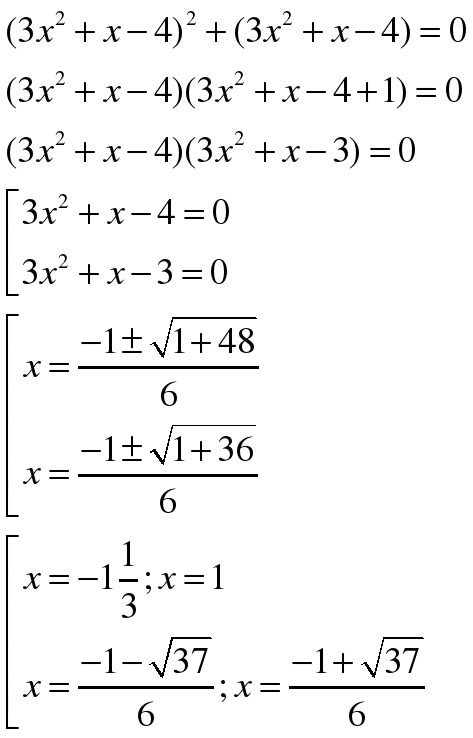
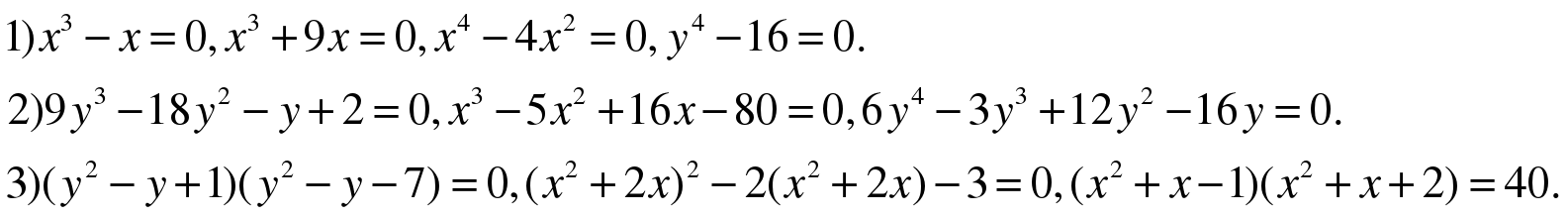

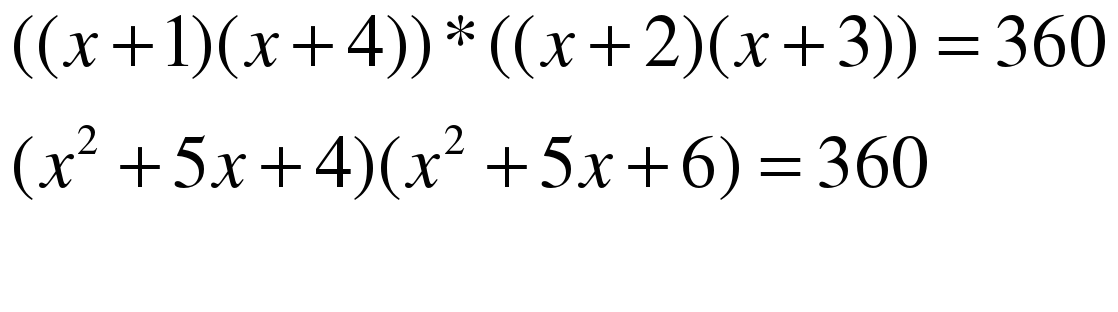 Замена:
Замена: