открытый урок по алгебре в 9 классе на 2 урока,урок-путешествие по стране "математика"
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Уравнения,приводимые к квадратным. Биквадратные уравнения.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Уравнения,приводимые к квадратным. Биквадратные уравнения.»
Полезное для учителя
Распродажа видеоуроков!
1970 руб.
2820 руб.
1760 руб.
2510 руб.
2020 руб.
2880 руб.
2100 руб.
3000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
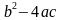 для квадратных уравнений с коэффициентами
для квадратных уравнений с коэффициентами 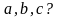
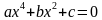 , где
, где 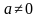
 .
.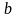 или
или 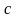 равен 0.
равен 0.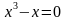 ,
, 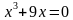 ,
, 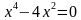 ,
, 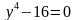 ;
;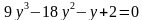 ,
, 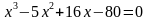 ,
, 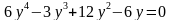 ;
;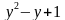 )(
)(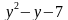 ) = 65,
) = 65, 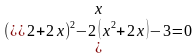 ,
, 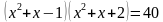 .
.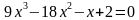 ; б)
; б) 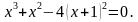
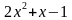 )(
)(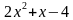 ) + 2 = 0
) + 2 = 0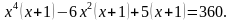 (ход решения комментируют с места).
(ход решения комментируют с места).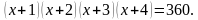
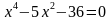 ; г)
; г) 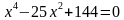 ;
;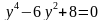 ; д)
; д) 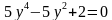 ;
;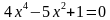 ; e)
; e) 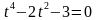 .
.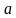 уравнение
уравнение  не имеет корней? (пример на повторение).
не имеет корней? (пример на повторение).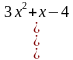 решите уравнение итальянских математиков.
решите уравнение итальянских математиков.















