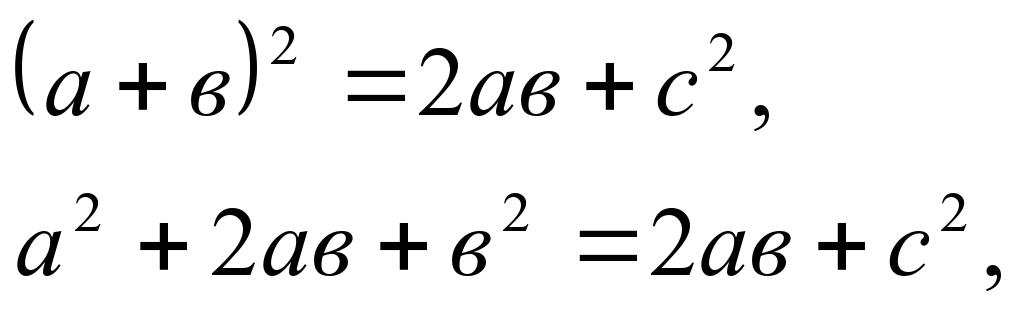| 1. | Учитель здоровается с классом, объявляет тему урока, постановку целей и задач перед учащимися: познакомиться с теоремой Пифагора, многообразием способов ее доказательства и ее применением при решении задач, а также повторить изученный ранее материал (площади треугольника, ромба, прямоугольника, квадрата, параллелограмма)
| Поприветствовать учителя, проверить готовы ли они к уроку. | Заранее подготовленная запись: число и классная работа. |
| 2. | 1. По данным рисунка найдите площадь четырехугольника АВСD.
Возможные вопросы учителя ученикам: а) что за четырехугольник изображен на рисунке?
б) можем ли мы сразу найти площадь этого четырехугольника?
в) давайте подумаем как можно это сделать? Каким свойством площадей нужно воспользоваться?
г) как найти площади этих треугольников?
д) как найти катет АС?
е) чему равен катет CD?
ж) какова же площадь четырехугольника АВ 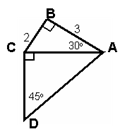
2. По данным рисунка докажите, что четырехугольник КМNР – квадрат (эта задача особенно важна, так как такая же фигура, как на рисунке, используется для доказательства теоремы). 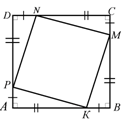 Возможные вопросы учителя ученикам: а) как доказать что четырехугольник является квадратом?
б) Что надо сделать, чтобы доказать, что MKPN квадрат? в)Как доказать , что стороны четырехугольника равны?
г) Давайте подумаем, как показать, что у этого ромба хотя бы один угол равен 90 градусов? Например угол Р.
д)Что можно сказать про углы DPN и APK? Чему равна их сумма?
е) Чему же равна градусная мера угла NPK?
Молодцы, вы хорошо справились с этими задачами, вспомнили свойство площадей, свойства прямоугольных треугольников, не забыли что такое квадрат.
| Дети выполняют подготовительные задания, представленным на интерактивной доске.
1. Ответы детей на вопросы учителя:
а) произвольный четырехугольник;
б) нет;
в) площадь четырехугольника АВСD равна сумме площадей двух треугольников, на которые он разбит;
г) т.к. эти треугольники прямоугольные, то их площади равны половине произведения катетов;
д) т.к. в прямоугольном треугольнике АВС против угла в 30 градусов лежит катет, равный половине гипотенузы, то гипотенуза АС равна 4 см. А она является катетом для треугольника АСD;
е) прямоугольный треугольник ACD является равнобедренным, поэтому CD=AC=4 см;
ж) 11 кв.см.
2. Ответы детей на воспросы учителя: а) квадрат – это прямоугольник, у которого все стороны равны;
б) докажем равенство сторон МК, КР, РN,NM. Затем попробуем найти его углы. в)рассмотрим четыре прямоугольных треугольника. Из рисунка видно, что они равны по двум катетам.Поэтому и их гипотенузы тоже равны.
г) Угол DPN+угол NPK+ угол APK=180 градусов.
д) Т.к.  PDN= PDN= KAP, то против равных катетов лежат равные углы, т.е. угол DPN= углу PKA и угол DNP= углу APK. А т.к. сумма острых углов прямоугольного треугольника 90 градусов, то угол DPN + угол APK = 90 градусов. KAP, то против равных катетов лежат равные углы, т.е. угол DPN= углу PKA и угол DNP= углу APK. А т.к. сумма острых углов прямоугольного треугольника 90 градусов, то угол DPN + угол APK = 90 градусов.
е) 90 градусов. | Задачи транслируются учащимся посредством презентации
S(ABCD)=S(ABC)+S(ACD)
S(ABC)=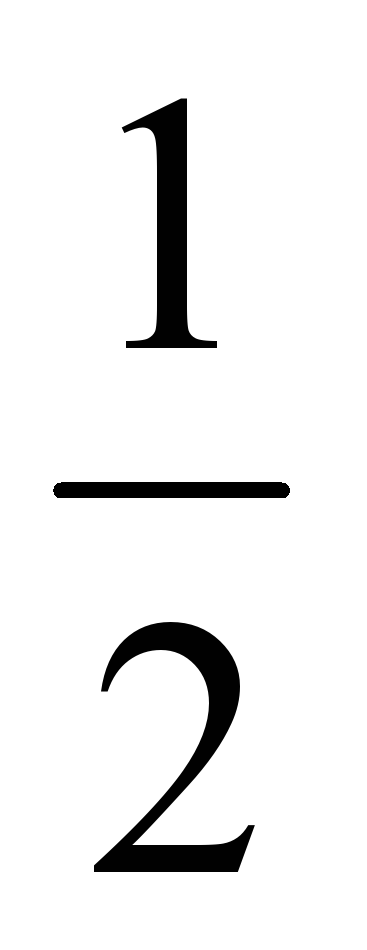 AB*BC AB*BC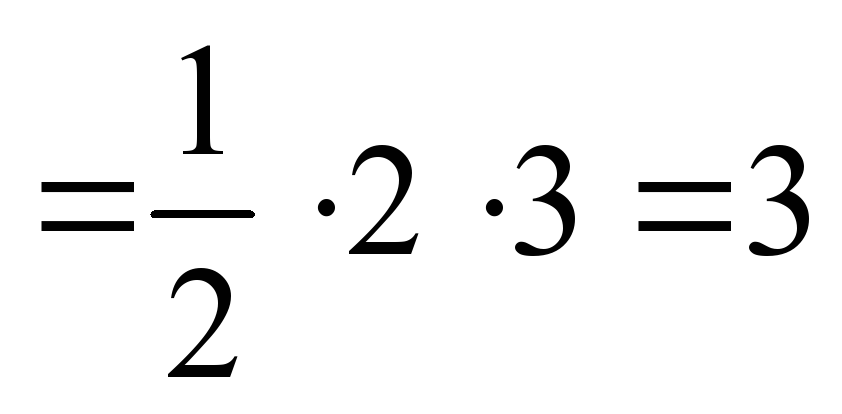 S(ACD)=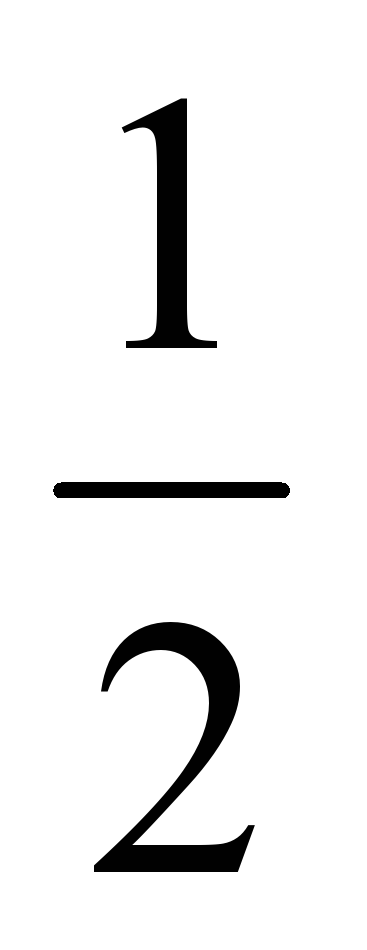 AC*CD AC*CD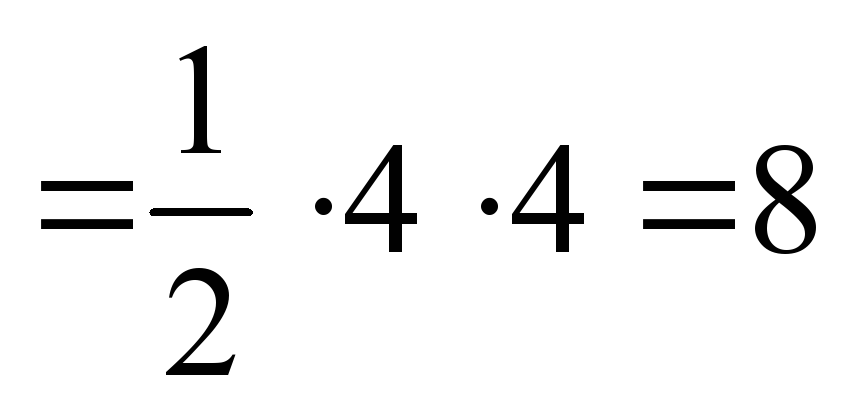
1.Р/м  PDN, PDN,  NCM, NCM,  MBK, MBK,  AKP (угол D=углу С=углу В=углу А) AKP (угол D=углу С=углу В=углу А)
DN=CM=BK=AP (по усл.)
PD=NC=NB=AK (по усл.)
Поэтому  PDN= PDN= NCM= NCM=  MBK= MBK= AKP (по 2-м катетам). AKP (по 2-м катетам).
Значит, PN=NM=MK=KP.
Т.е. PNMK-ромб. 2. DPN+ DPN+  NPK+ NPK+  APK=180. APK=180.
 DPN = DPN = PKA. PKA.
 DNP = DNP = APK. APK.  DPN+ DPN+ DNP=90. DNP=90.
Поэтому  NPK=90. NPK=90.
3.Ромб, у которого хотя бы один угол прямой является квадратом.
|
| 3.
4. | Практическая работа:
1.Постройте в тетрадях прямоугольный треугольник (с катетами, длина которых для удобства выражается натуральными числами).
2.Измерьте катеты и гипотенузу. Результаты измерений запишите в тетрадях.
3.Возведите все результаты в квадрат, т.е узнайте величины 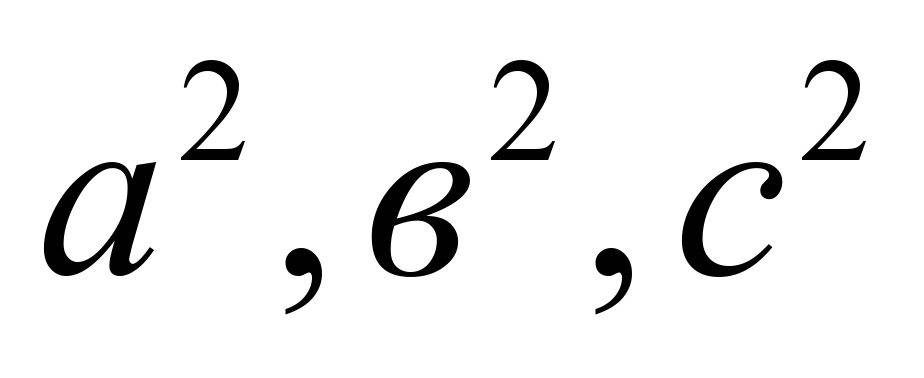 . .
4. Сложите квадраты катетов 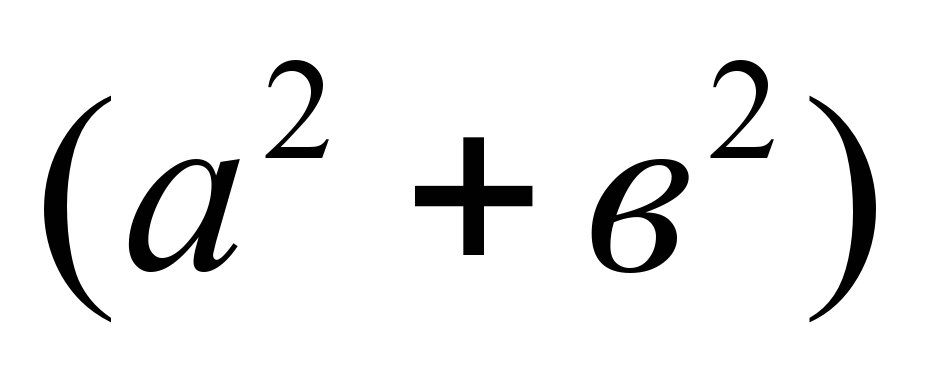 и сравните с квадратом гипотенузы. и сравните с квадратом гипотенузы.
5. Что у вас получилось? Какой можно сделать вывод? Учитель: «То, к чему мы пришли опытным путем, доказал древнегреческий ученый Пифагор в 6 в. до н. э. Он не открыл эту теорему (она была известна еще в Древнем Египте и Вавилоне), а нашел ее доказательство. Неизвестно, каким способом доказывал Пифагор свою теорему. Несомненно лишь то, что он открыл ее под сильным влиянием египетской науки. Частный случай теоремы Пифагора — свойство треугольника со сторонами 3, 4 и 5 — был известен строителям пирамид задолго до рождения Пифагора, сам же он более 20 лет обучался у египетских жрецов. Сохранилась легенда, которая гласит, что доказав свою знаменитую теорему, Пифагор принес богам в жертву быка, а по другим источникам даже 100 быков. Это, однако, противоречит сведениям о моральных и религиозных воззрениях Пифагора. В литературных источниках можно прочитать, что он «запрещал даже убивать животных, а тем более ими кормиться, ибо животные имеют душу, как и мы». Пифагор питался только медом, хлебом, овощами и изредка рыбой. В связи со всеми этим более правдоподобной можно считать следующую запись: «…и даже когда он открыл, что в прямоугольном треугольнике гипотенуза имеет соответствие с катетами, он принес в жертву быка, сделанного из пшеничного теста». Известно более 100 доказательств этой теоремы. Приведем только одно из них.»
Учитель: «Итак, сегодня мы изучаем одну из самых известных геометрических теорем древности, называемую теоремой Пифагора. Давайте ее сформулируем»
Теперь давайте докажем этот факт.
1.Назовите мне условие теоремы.
2.Каково заключение теоремы.
3. Учитель: «1.Достроим треугольник до квадрата со стороной 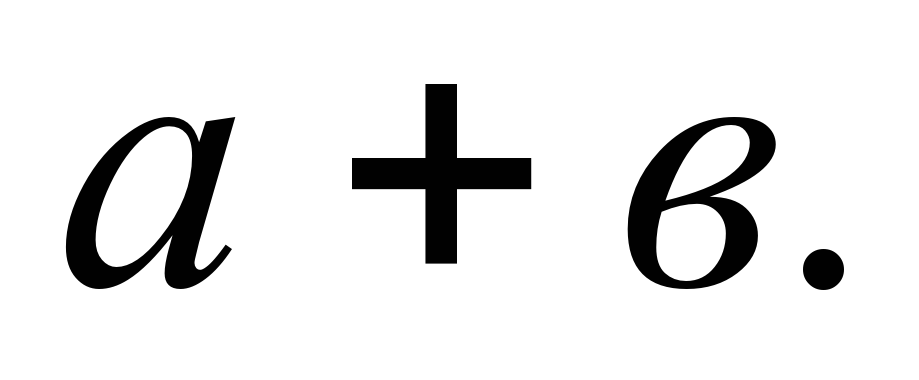
2.Как найти площадь этого квадрата?
3. На какие фигуры разбит квадрат?
4. Как найти по-другому площадь этого квадрата?
5.как находится площадь прямоугольного треугольника?
6.Т.к. мы находили площадь одного и того же квадрата, то правые части равенств можно приравнять.
Знаменитая теорема Пифагора звучала так: Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов построенных на его катетах.   Про картинку, иллюстрирующую эту теорему, сложена шутливая поговорка: «Пифагоровы штаны на все стороны равны». Что имелось ввиду?
| Учащиеся выполняют практическую работу в тетрадях
Квадрат гипотенузы равен сумме квадратов катетов.
Учащиеся записывают в тетрадях тему урока – «Теорема Пифагора».
Учащиеся записывают формулировку теоремы Пифагора.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
1.Прямоугольный треугольник.
2.квадрат гипотенузы равен сумме квадратов катетов.
3.2. Площадь квадрата равна квадрату его стороны.
3.3. Четыре прямоугольных треугольника и квадрат.
3.4. Сложить площади фигур, на которые он разбит.
3.5. площадь прямоугольного треугольника равна половине произведения катетов.
Дети отвечают на поставленные вопросы : сторону квадрата возвести в квадрат, квадрат гипотенузы, квадраты катетов.
|
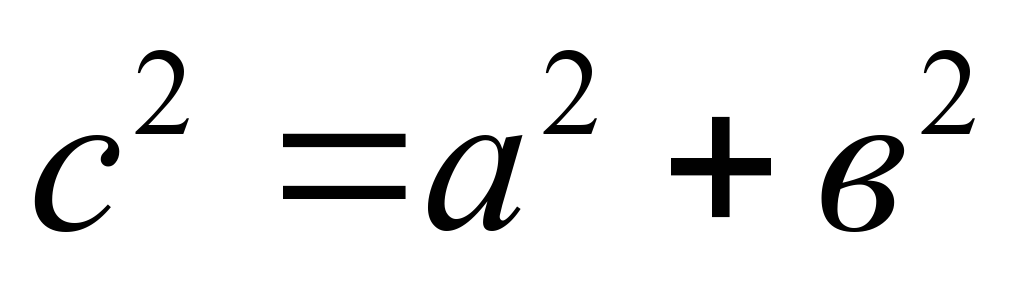
 А в а А в а  а в а в в а С В а в Дано: ,АВ=с, ВС=а, АС=в ,АВ=с, ВС=а, АС=в
Док-ть: 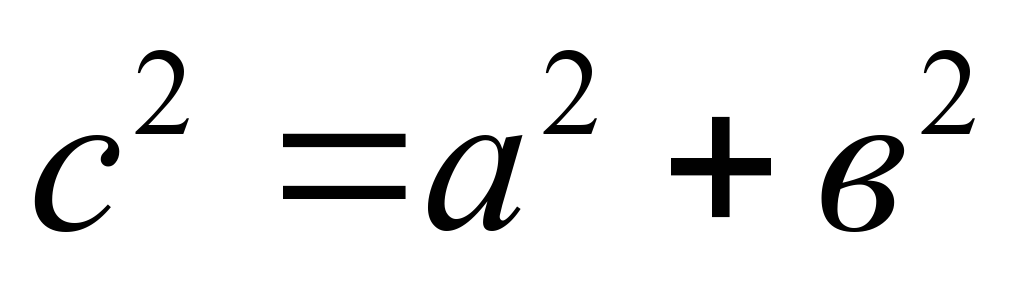
Док-во: 1.Площадь S этого квадрата равна 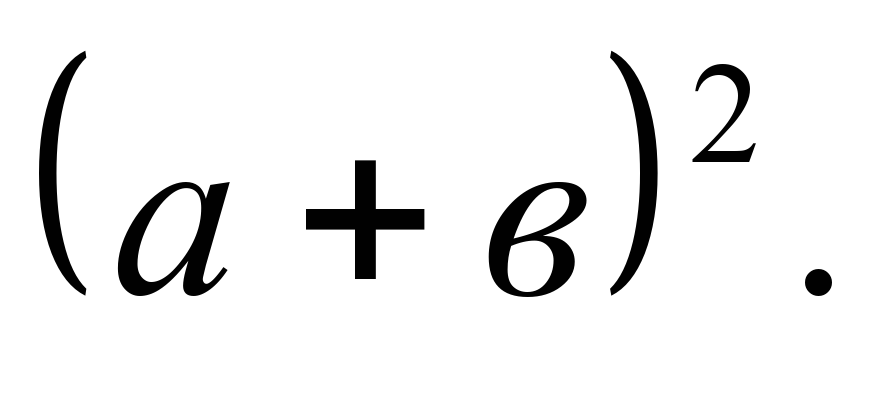 2.С другой стороны, этот квадрат составлен из четырех равных прямоугольных треугольников, площадь каждого из которых равна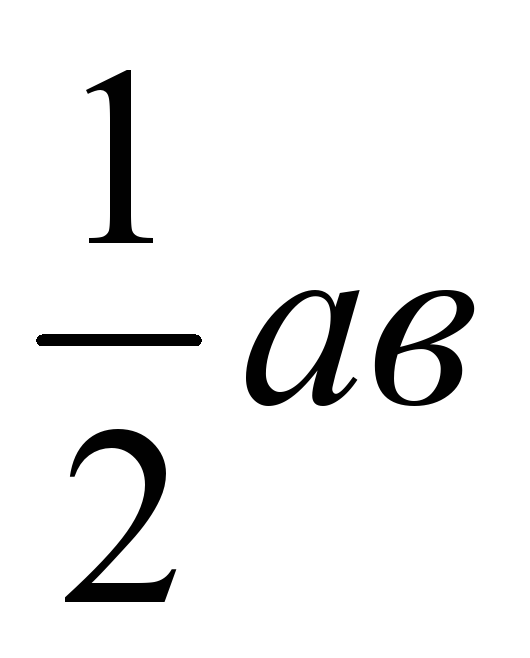 , и квадрата со стороной , и квадрата со стороной  , поэтому , поэтому 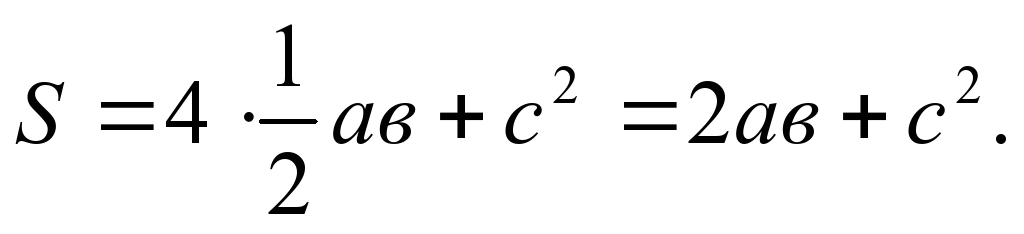
3.Таким образом,
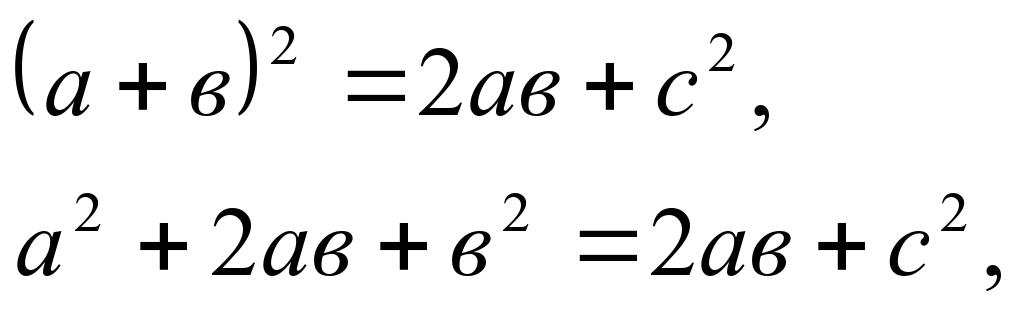
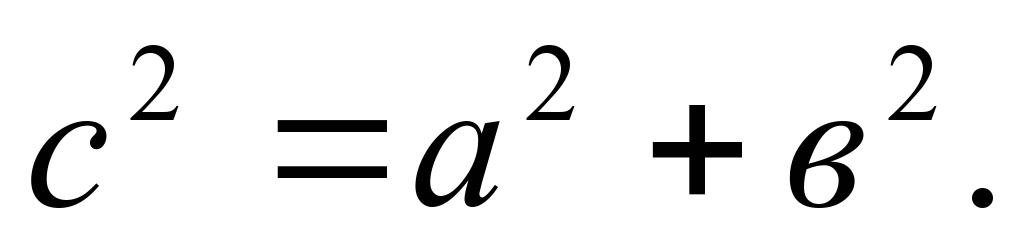 Теорема доказана.
|
5. | Рефлексия:Организация рефлексии на основе метода неоконченных предложений Ответь на 5 любых предложений.
Я почувствовал, что…
Было интересно…
Меня удивило…
Своей работой сегодня я…, потому что...
Мне захотелось…
Мне больше всего удалось…
Заставил задуматься…
Сегодня я узнал…
Было трудно…, потому что...
Я выполнял задания…
Я понял, что…
Теперь я могу…, потому что...
Я приобрёл…
Я научился…
Задания для меня показались…, потому что...
Для меня было открытием то, что…
Мне показалось важным…, потому что... Учитель объявляет домашнее задание: « 1.Выучить формулировку и уметь доказывать теорему Пифагора тем способом, который применяли на уроке.
2.индивидуальное задание сильным учащимся – найти и подготовить другое доказательство теоремы Пифагора.
Урок окончен, можете быть свободны» | Дети записывают в дневник домашнее задание | на интерактивной доске выведено домашнее задание. |




 А в а
А в а  а в
а в