Данная работа представляет собой методическую разработку рассчитаны на учащихся 6 класса первого урока по теме «Сокращение дробей».
Задачи урока: проверка знаний учащимися фактического материала, умений применять знания при решении поставленных задач, совершенствование вычислительных навыков; развитие навыков самостоятельности, самоконтроля, самооценки.
Каждый ученик в ходе урока выполняет определенные задания, самостоятельно оценивает себя за каждое задание и выставляет отметку в индивидуальный оценочный лист. По итогам занятия по сумме набранных баллов учащиеся оценивают свою работу и анализируют, насколько успешной была его деятельность на уроке.
На уроке формируются УУД учащихся: коммуникативные, регулятивные, познавательные, личностные.
| ФИО | Журавлева Наталья Владимировна |
| Место работы | МКОУ СОШ с.Лазарево |
| Должность | Учитель математики |
| Предмет | Математика |
| Класс | 6 |
| Базовый учебник | Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6: Учебник для учащихся общеобразовательных учреждений, 30 издание, стереотипное. – М. Мнемозина, 2013 |
| Название урока | Сокращение дробей |
| Тип урока | Урок формирования новых знаний и умений |
| Форма проведения урока | Традиционная |
| Образовательная среда урока | Компьютер, проектор, учебники по математике, раздаточный материал, индивидуальные карты оценки учеников. |
| Формы работы учащихся | Фронтальная, индивидуальная, парная |
| Цель урока | Для учителя | Для ученика | Метапредметные результаты |
|
| Ввести понятие сокращения дробей и познакомиться с понятием «несократимая дробь». Научиться сокращать дроби, используя основное свойство дроби и применять признаки делимости чисел. | Вывести алгоритм сокращения дробей и научиться применять его на практике. | Регулятивные – развивать умение видеть математическую задачу в контексте проблемной ситуации в окружающей жизни; совершенствовать критерии оценки и использовать их в ходе оценки и самооценки. Познавательные – понимать сущность составления алгоритма, действовать по алгоритму, проговаривать выводы в виде правил «если …, то …». Коммуникативные – уметь оформлять свои мысли в устной и письменной речи с учётом речевых ситуаций; уметь слушать собеседника и вести диалог, работать в паре. Личностные - адекватно оценивать результаты своей учебной деятельности, осозновать и принимать социальную роль ученика, объяснять свои достижения, понимать причины успеха в учебной деятельности. |
| Задачи урока:
Обучающая – сформулировать правило сокращения дробей; сформировать умение пользоваться этим правилом. Развивающая – развивать логическое мышление, память, познавательный интерес, продолжить формировать математическую речь, вырабатывать умение анализировать и сравнивать, развивать навыки самоконтроля. Воспитывающая – развитие любознательности и интереса к предмету, воспитание у учащихся навыков учебного труда, формирование ответственности за конечный результат, доброжелательного отношения друг к другу. |
| Этапы урока
| Деятельность учителя
| Деятельность ученика
| Формируемые УУД
|
|
Организационный ( 1 мин) |
Приветствие учащихся. Проверка учителем готовности класса к уроку; организация внимания.
Почему так говорят? О математике: Математика – царица наук. Математика – дверь и ключ ко всем наукам. Об арифметике: Арифметика – царица математики. О дробях: Кто не познал дроби, то не познал математики. А значит … Без математических знаний человек не может сформироваться как гармоническая личность. Поэтому давайте продолжать осваивать математику, каждый день добывая новые и новые знания, которые помогут в изучении других предметов и в нашей практической жизни. Устный счет Машинистка выполнила работу за 7 дней. Какую часть работы она выполнит за 1 день? (1/7) Туристы от базы до озера шли 4 ч со скоростью 6 км/ч.
А) Каково расстояние от базы до озера? (24 км)
Б) С какой скоростью они шли обратно, если обратный путь занял 3 часа? (8 км/ч) По учебнику №253(а, б) (автор Н.Я. Виленкин).
|
Слушают учителя, настраиваются на работу, проверяют готовность к уроку.
Ответы учеников
Эффект соревнования с коментариями |
Умение слушать других и вступать в диалог. Умение выделять нравственный аспект поведения.
|
|
Актуализация знаний ( мин) |
Поработаем устно:
1. Что называется делителем натурального числа? 2. Что называется НОК чисел a и b? 3. Что называется НОД чисел a и b? 4. Какие числа называются простыми? 4. Какие признаки делимости вы знаете? 5. Основное свойство дроби. Напишите 2-3 равные дроби.
Если числитель и знаменатель дроби умножить или разделить
на одно и то же натуральное число, то получится равная ей дробь.
Это свойство называют основным свойством дроби.
пример: 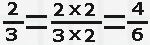
Две равные дроби являются различными записями одного и того же числа. Для закрепления теоритического материала учащиеся выполняют графический диктант. Ответ «да» соответствует _ , ответ «нет» соответствует /\. 









Ключ _ _ _ _ _ /\ _ /\ /\ /\
«5» – 10 заданий «4» – 8, 9 заданий «3» – 5, 6, 7 заданий «2» – меньше 5 заданий |
Отвечают на вопросы работая в парах, повторяют материал предыдущих уроков.
Выполняют задания графического диктанта, оценивают сами свой результат, работая в парах исправляют свои ошибки и ошибки соседа, выставляют отметку в оценочный лист.
|
Познавательные: применение предметных знаний; выполнение учебных заданий. Регулятивные: Выделение и осознание того, что уже пройдено; Умение распознавать на слух вопросы и отвечать на них. Коммуникативные: Умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог. Личностные: Самоооценка, взаимооценка. |
|
Актуализация знаний. Постановка цели и задач урока. Мотивация учащихся. ( мин) |
А теперь откроем учебник, стр. 40, задача № 250. Прочтите, пожалуйста, вслух задачу. Поставьте вопросы на которые вам надо ответить, что бы решить задачу.
вам 2минуты, чтобы вы в парах обсудили решение данной задачи.
Выслушать мнения учащихся, записать решение на доске: 1) 6 : 16 = 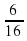 (ч) затратил первый рабочий (ч) затратил первый рабочий 2) 15 : 24 = 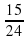 (ч) затратил второй рабочий (ч) затратил второй рабочий 
Как сравнить две дроби с одинаковыми знаменателями? А сравнивать дроби с разными знаменателями? – Можем ли мы из этих дробей получить равные им дроби, но с другими знаменателями? – Какое свойство мы для этого используем? 

– Итак, мы с вами применили основное свойство дроби, заменили дроби на равные им путём деления числителя и знаменателя на одно и то же число. В учебники найдите как называется такое действие с дробями? Определите тему урока. Запишите её в тетрадь.
– А теперь попробуйте сформулировать цель нашего урока, с чем мы должны познакомиться и чему научиться на уроке.
Ставим перед собой цель вывести правило сокращения дробей, используя признаки делимости чисел и основного свойства дроби, и уметь применять его на практике.
Задачи 1. Сформулировать правило сокращения дробей 2. Ввести понятие несократимой дроби 3. Научиться применять эти правила при решении заданий
|
Подготовка к восприятию нового материала. О чем задача? Сколько было рабочих? Что говорится в задаче об этих рабочих? Что нужно найти? Что для этого нужно знать?
Обсуждают в парах решение задачи.
Применяем основное свойство дроби
– Нужно сравнить дроби.
Читают параграф и записывают тему урока
Комментируют полученный результат. Выявляют проблему, формулируют тему урока, ставят цель. Записывают тему урока.
|
Познавательные: Извлечение из текстов математической информации; Постановка и формулирование проблемы; Самостоятельное формулирование познавательной цели. Регулятивные: Умение анализировать, Целеполагание. Прогнозирование. Коммуникативные: Умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог, участвовать в коллективном обсуждении проблем. Работать в паре. Личностные: Самооценка. |
|
Усвоение новых знаний. ( мин)
| – Давайте вместе попробуем сформулировать правило, что такое сокращение дробей и как сократить дробь. Как сократить дробь? Правило сокращения дробей Осталось лишь разобрать правило сокращения дробей, которое и объясняет, как сократить данную дробь. Правило сокращения дробей состоит из двух шагов: во-первых, находится НОД числителя и знаменателя дроби; во-вторых, проводится деление числителя и знаменателя дроби на их НОД, что дает несократимую дробь, равную исходной. – откройте учебник на стр. 39, прочитайте, выучите правило, расскажите его друг другу.
– Попробуйте сформулировать определение несократимой дроби. (Если числитель и знаменатель дроби взаимно простые числа, то их НОД равен 1 и такая дробь несократима.) |
Выполняют вместе с учителем задания. Отвечают на вопросы учителя. Выдвигают предположения. Формулируют правило, отвечают друг другу, оценивают ответы.
|
Познавательные: Структурирование знаний, Выбор способов решения задач, Анализ объектов и синтез. Регулятивные: Умение оценивать правильность выполнения действия; Планирование пути достижения цели; прогнозирование. Коммуникативные: развитие умения слушать и вступать в диалог, задавать вопросы. Личностные: Осознание ответственности за общее дело |
| Динамическая пауза
| Раз – подняться, потянуться, Два – согнуться, разогнуться. Три – в ладоши три хлопка, Головою тори кивка. На четыре - руки шире, Пять – руками помахать, Шесть – за парту сесть опять.
|
|
|
|
Выполнение учащимися заданий на закрепление пройденного правила. ( мин) |
наши новые знания надо попробовать применить на практике и проанализировать полученный результат. Сократить дроби, применяя понятие НОД, комментируя:

Сократить дроби самостоятельно. 
– Самооценка: «5» – все 6 заданий выполнены правильно «4» – 4 задания выполнены правильно «3» – 2 задания выполнено правильно
Самостоятельное решение с самопроверкой в режиме он-лайн на компьютере. Сократите дроби: Сократите дроби: Какую часть килограмма составляют :1 г, 25 г, 500 г, 443 г. Какую часть прямого угла составляют: 1°, 60°, 15°.
|
Отвечают на вопросы учителя, задают вопросы если возникли затруднения Выполняют письменное задание в тетради и у доски.
Решают примеры самостоятельно в тетради, у доски решают те же примеры на доске, потом вместе с классом проверяют. Учащиеся проверяют свой результат, выставляют отметку в оценочный лист.
Решают задания с самопроверкой в режиме он-лайн на компьютере.
|
Познавательные: Уметь решать примеры по выбранному правилу; Применение предметных знаний, выбор способов решения задач. Регулятивные: Умение проговаривать последовательность действий на уроке, анализировать и оценивать результат работы; Коммуникативные: Умение слушать, обращаться с вопросом к учителю и сверстнику Личностные: Самооценка. |
|
Подведение итогов урока. Постановка домашнего задания. ( мин) |
пора подвести итоги и записать домашнее задание: §9, № 268 (а, б), 271 (а, б), 274 (а) правило выучить
– Что значит сократить дробь? – Что меняется при сокращении дроби? – Какая дробь называется несократимой? – Поставьте себе оценку за урок. Я попрошу вас в тетради их выставить.
|
Отвечают на вопросы учителя. Записывают домашнее задание. Подсчитывают общее количество баллов за урок и выставляют себе отметку и помогают соседу.
|
Познавательные: Выделение и формулирование познавательной цели, рефлексия способов и условий действия. Анализ и синтез объектов. Регулятивные: Оценка-осознание уровня и качества усвоения. Коммуникативные: Умение с достаточной полнотой и точностью выражать свои мысли. Личностные: Самооценка, Ценностно-смысловая ориентация |
| Рефлексия. ( мин) |
О чем мы сегодня говорили? Какую цель мы поставили сегодня? Достигли ли мы этой цели? Все ли было понятно?
А теперь крепко потрите свои ладошки, так, чтобы стало жарко. Быстро передайте тепло другу, соединив свои ладошки с ладошками соседа.
- На этом мы и заканчиваем наш урок. Пусть тепло души ваших друзей согревает вас.
Урок окончен! Спасибо за работу! | Рефлексия. | Познавательные: Рефлексия Регулятивные: Оценка своей деятельности и деятельности других людей Коммуникативные: Умение с достаточной полнотой и точностью выражать свои мысли Личностные: Самооценка на основе критерия успешности. |










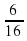 (ч) затратил первый рабочий
(ч) затратил первый рабочий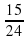 (ч) затратил второй рабочий
(ч) затратил второй рабочий



















