Теңбүйірлі үшбұрыш және оның қасиеттері

7.3А бөлім: Үшбұрыштар

Күні:

Мұғалімнің аты-жөні:

Сынып: 7

Қатысқандар саны:

Қатыспағандар саны:

Сабақ тақырыбы

Тең бүйірлі үшбұрыш және оның қасиеттері

Оқу мақсаттары

7.3.1.23

теңбүйірлі үшбұрыштың белгілері мен қасиеттерін қолдану;

Сабақ мақсаттары

Тең бүйірлі үшбұрыштың қасиеттерін, белгілерін білу.

Есептер шығаруда қолдану

Жетістік критерийлері

тең бүйірлі үшбұрыштың қасиеттерін біледі

тең бүйірлі үшбұрыштың белгілерін біледі

есептерді шығару барысында тең бүйірлі үшбұрыштың қасиеттері мен белгілерін қолданады

Тілдік мақсаттар

Оқушылар

үшбұрыштар түрлерінің айырмашылығын анықтайды және әрбірінің қасиеттерін ауызша және жазбаша сипаттай алады.

Оқушылар үшбұрыштардың теңдігін дәлелдеу кезіндегі өз қорытындыларын негіздейді.

Құндылықтарды дарыту

Топтық талқылау барысында сөздік қоры дамиды, академиялық шынайылық қалыптасады. Достық, адамгершілік қасиеттері артады.

Пәнаралық байланыстар

Геометрия пәні

АКТ қолдану дағдылары

Ақпаратты табу, қосымшаларды пайдалану арқылы АКТ-ны қолдану.

Бастапқы білім

Үшбұрыштың медианасының, биссектрисасының және биіктіктігінің анықтамасы және оларды кескіндеу;

сүйір бұрышты, тік бұрышты және доғал бұрышты үшбұрыштардың биіктіктерінің орналасуын салыстыру;

Сабақ барысы

Сабақтың жоспарланған кезеңдері

Сабақтағы жоспарланған іс-әрекет

Ресурстар

Сабақтың басы

3 мин.

8 мин

Сабақтың ортасы

10 мин

2 мин

10 мин

І. Ұйымдастыру кезеңі

О қушыларды түрлі үшбұрыштардың суреттері бойынша 4 топқа бөлу. Топтарға біріктіре отырып бір-бірімен ой бөлісуге, бір-бірінің пікіріне құрметпен қарап, сыныпта ынтымақтастық атмосфераны қалыптастыруды дамыту.

ІІ. Үй тапсырмасын тексеру. Оқушыларға үй жұмысының жауаптары бар таратпа парақтар таратып беру. Үйге берілген тапсырманы қасында отырған оқушыға тексерту арқылы өз жұмысындағы қателіктерін еске түсіру. Үй тапсырмасында байқалған кемшіліктерді жою, оның пайда болу себептерін анықтау. Өз жұмысын пайыздық жолмен бағалай отырып оқушыларға құндылықтарды дарыту

Өткен тақырып бойынша үшбұрыштың түрлерін талдайды,

нені білдіретінін, оның анықтамаларын немесе қасиеттері болса атап көрсетуін айтамын. (топпен орындайды)

Кестені толтырғаннан кейін дайын жауаптары бойынша топтар алмасып тексереді. Үшбұрыштың түрлеріне анықтамаларды беріп кетеді.

Үшбұрыштардың өмірде қолданылуына тоқталу.

ІІ. Жаңа сабақ. Оқушыларды сабақтың мақсатымен таныстыру. Теңбүйірлі үшбұрыштың анықтамасын және элементтерін жетекші сұрақтар арқылы анықтайды. (анықтама береді)

Екі қабырғасы тең үшбұрышты тең бүйірлі үшбұрыш деп атайды. Тең қабырғаларын үшбұрыштың бүйір қабырғалары деп, ал үшінші қабырғасын оның табаны деп атайды.

Слайдта көрсетілген үшбұрыштардың табаны мен бүйір қабырғаларын ауызша атап өтеді. (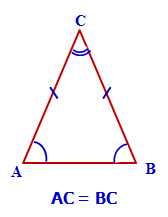 мақтау, мадақтау арқылы бағаланады)

IV.Теоремаларды дәлелдеу. Топтық жұмыс

Оқушылар берілген теоремаларды өздігінен дәлелдейді топта талқылайды. (Ресурс парақтары мен оқулықпен жұмыс жасап бір-бір теоремадан дәлелдеп шығады).

І топ. Теорема 1: Теңбүйірлі үшбұрыштың табанындағы бұрыштары тең болады

ІІ топ.Теорема 2. Егер үшбұрыштың екі бұрышы тең болса, онда ол үшбұрыш теңбүйірлі үшбұрыш болады.

ІІІ топ. Теорема 3. Тең бүйірлі үшбұрыштың төбесінен табанына жүргізілген биссектрисасы оның әрі медианасы, әрі биіктігі болады.

Дәлелдеуі:

Теорема 3. Тең бүйірлі үшбұрыштың төбесінен табанына жүргізілген биссектриссасы оның әрі медианасы, әрі биіктігі болады.

Дәлелдеу. ∆ABC – табаны AB болатын теңбүйірлі үшбұрыш, ал CD – оның табанына жүргізілген биссектрисасы болсын.

С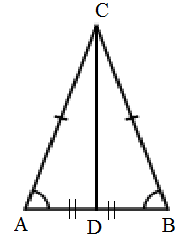 D кесіндісі осы үшбұрыштың әрі медианасы, әрі биіктігі болатынын көрсету керек.

Шынында да, СD биссектриса болғандықтан,

∠ACD =∠BCD, ал ∆ABC – теңбүйірлі болғандықтан АС=ВС. Осыған қоса СD кесіндісі -ACD және BCD үшбұрыштарына ортақ қабырға.Олай болса, үшбұрыштар теңдігінің І белгісі бойынша ∆ACD =∆BCD.Сондықтан AD=BD, яғни СD- медиана және ∠ADC =∠ BDC=90⁰, яғни сыбайлас бұрыштар теңдігінен CD АВ екенін аламыз. Онда CD әрі биіктік болады.

Нәтижесінде: Әрбір «іздеушілер» тобы өз шешімдерін постерге жазады, жұмыс аяқталған соң өздерінің «зерттеулерін» басқа оқушыларға көрсетеді. Постер арқылы дәлелдейді, басқа топтың мүшелері сұрақтар қояды немесе толықтырады

Оқушылардың білімін бекітуге арналған тапсырмалар.

Кері байланыс. (2 минут)

Ауызша тапсырмаларды орындау.

«5 СҰРАҚ» (ақиқат немесе жалған жауап беру.)

1. Үшбұрыштың ішкі бұрыштарының қосындысы 180⁰-қа тең.

2. Теңбүйірлі үшбұрыштың табанындағы бұрыштары тең емес

3. Тең бүйірлі үшбұрыштың бүйір қабырғасына жүргізілген биіктігі оның әрі биссектрисасы, әрі медианасы болады.

4. Теңбүйірлі үшбұрыштың табанындағы бұрышы 30⁰ тең болса, онда бүйір қабырғалары арасындағы бұрышы табандағы бұрышынан 4 есе үлкен болады.

5. Теңбүйірлі үшбұрыштың периметрі 32 см табан қабырғасының ұзындығы 8 см тең. Онда табаны бүйір қабырғасынан 2 см қысқа.

жұппен жұмыс: Жаңа сабақтан алаған білімдерін бағалау мақсатында жеке тапсырма беріледі. Қалыптастырушы бағалау

1-тапсырма. Қосымша №1

Дескриптор.

• теңбүйірлі үшбұрыштың қасиеттерін қолданады;

• сыбайлас және вертикаль бұрыштардың қасиеттерін қолданады;

• есептеулер орындайды;

• есептің жауабын табады.

Жеке жұмыс.

2-тапсырма. Теңбүйірлі үшбұрыштың бүйір қабырғасы табанынан үш есе үлкен. Периметрі 49см. Теңбүйірлі үшбұрыштың қабырғаларының ұзындықтарын табыңыз.

Дескриптор.

• үшбұрыштың периметрі формуласын қолданады;

• шарт бойынша теңдеу құрады;

• теңдеуді шешеді;

• есептің жауабын табады.

Оқушыларға есептерді шығару үшін шығармашыл болу керек екенін ескерте отырып, жеке жұмыста қолдау көрсетіп отыру.

Слайд№1-5

Слайд№6

Слайд№7-11

Слайд №1-2

Слайд №3

Слайд№ 4-5

Слайд № 6

Слайд

№7-13

Слайд

№14

Слайд

№16-17

Сабақтың соңы

5 мин

2 мин

Сабақты қорытындылау

Ауызша сұрақтар арқылы сабақты қорытындылау.

«Тиімді сұрақ –ұтымды жауап»

1.Теңбүйірлі үшбұрыштың табанындағы бұрыштары қандай болады

2.Тең бүйірлі үшбұрыштың төбесінен табанына жүргізілген биссектрисасы оның әрі медианасы, әрі биіктігі бола алады ма, неге?

3. Егер үшбұрыштың екі бұрышы тең болса, онда ол үшбұрыш теңбүйірлі үшбұрыш бола алады ма, неліктен?

Бағалау.

 Үйге тапсырмасы:

Үй тапсырмасын күнделіктеріне белгілейді. Теңбүйірлі үшбұрыштың қасиеттері мен белгілерін қолдана отырып екі есептен құрастыру.

7 сыныпқа арналған Ә.Н Шыныбеков Геометрия -7, В тобы №10.5.бет 60

Рефлексия:

бүгінгі сабақтың теориялы бөлімін түсіндім және есептер шығаруда қолдана алдым

бүгінгісабақтың теориялық бөлімін түсіндім, бірақ есептер шығаруда қолдана алмадым.

мен теориялық бөлімді жақсы түсінбедім, сондықтан есеп шығаруда қолдана алмадым.

Слайд №18

Слайд № 20

Слайд № 21

http://www.mathsisfun.com/triangle.html

http://bilimland.kz/ru/

Саралау – оқушыларға қалай көбірек қолдау көрсетуді жоспарлайсыз? Қабілеті жоғары оқушыларға қандай міндет қоюды жоспарлап отырсыз?

Бағалау – оқушылардың материалды меңгеру деңгейін қалай тексеруді жоспарлайсыз?

Қиынырақ есептер беріп, олардың нәтижесімен қорытынды жасату

Жеке тапсырмалар беру арқылы

Денсаулық және қауіпсіздік техникасының сақталуы

Сабақ бойынша рефлексия

Сабақ мақсаттары/оқу мақсаттары дұрыс қойылған ба? Оқушылардың барлығы ОМ қол жеткізді ме?

Жеткізбесе, неліктен?

Сабақта саралау дұрыс жүргізілді ме?

Сабақтың уақыттық кезеңдері сақталды ма?

Сабақ жоспарынан қандай ауытқулар болды, неліктен?

Бұл бөлімді сабақ туралы өз пікіріңізді білдіру үшін пайдаланыңыз. Өз сабағыңыз туралы сол жақ бағанда берілген сұрақтарға жауап беріңіз.