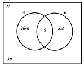
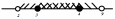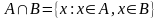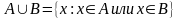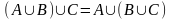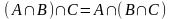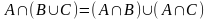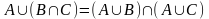Тема: Понятие множества
.
Цели урока:
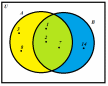
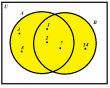
Образовательные: ввести определение множества, пересечения, объединения, разности конечных и бесконечных множеств; научить находить пересечение, объединение, разность конечных и бесконечных множеств (ПК1); изображать эти множества с помощью диаграммы Венна, с помощью числовых интервалов (ПК1); продолжить формировать умение находить множество решений неравенства, множество допустимых значений функции в простых и более сложных случаях;
Воспитательные: создать условия для воспитания в учащихся взаимоуважения, умения вести беседу, задавать соответственные теме вопросы (КК1); учить соблюдать моральные принципы при работе в группе, этику общения в процессе взаимодействия с людьми (КК4);
Развивающие: применять имеющиеся знания при решении нестандартных задач (ПК2).
Тип урока: формирующий новые понятия, знания.
Используемые на уроке методы: Перестрелка вопросами, частично-поисковый, табличный анализ и сравнение, диаграмма Венна, работа в мини-группах, исследовательский.
Используемые учебные материалы и электронные ресурсы: мел, доска,карточки.
Вводимые компетенции: КК1(коммуникативная), КК4 (активной гражданской позиции), ПК1 (предметная), ПК2 (когнитивная)
По завершению урока учащиеся должны:
- суметь грамотно и четко дать определение множества, конечного и бесконечного множества;
- найти пересечение, объединение, разность множеств;
- приводить примеры таких пересечения, объединения и разности множеств;
- уметь изображать их с помощью диаграммы Венна и интервалов на числовой прямой;
- в простых случаях уметь самостоятельно находить множество допустимых значений алгебраического выражения.