Разработка содержит конспект урока геометрии «Сумма углов треугольника», презентацию «Многоугольники», учебную программу Динамическая геометрия для создания многоугольников и измерения их углов. В ходе объяснения материала обучающиеся самостоятельно выводят формулы для нахождения числа диагоналей многоугольника, числа треугольников, на которые разбивается многоугольник диагоналями.
- Меню
- Главная
- Дошкольное образование
- Начальные классы
- Астрономия
- Биология
- География
- Информатика
- Математика
- Алгебра
- Геометрия
- Химия
- Физика
- Русский язык
- Английский язык
- Немецкий язык
- Французский язык
- История
- Естествознание
- Всемирная история
- Всеобщая история
- История России
- Право
- Окружающий мир
- Обществознание
- Экология
- Искусство
- Литература
- Музыка
- Технология (мальчики)
- Технология (девочки)
- Труд (технология)
- Физкультура
- ИЗО
- МХК
- ОБЗР (ОБЖ)
- Внеурочная работа
- ОРК
- Директору
- Завучу
- Классному руководителю
- Экономика
- Финансовая грамотность
- Психологу
- ОРКиСЭ
- Школьному библиотекарю
- Логопедия
- Коррекционная школа
- Всем учителям
- Прочее
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
- Главная
- Математика
- Уроки
- Сумма углов многоугольника
Сумма углов многоугольника
Просмотр содержимого документа
«01 Primary Figures»
1. Геометричні фігури
На рисунку 1.1 зображено декілька геометричних фігур, побудованих у середовищі пакета динамічної геометрії DG. Для того щоб отримати уявлення про можливості пакета змініть положення базових точок рисунка (вони позначені червоними квадратиками). Ви помітите, що положення геометричних фігур при цьому змінюються, змінюється їх взаємне розташування, змінюються розміри фігур, проте деякі важливіші властивості фігур при цьому зберігаються. Ті властивості геометричних фігур, що не змінюються під час рухів і змін масштабу1, і є геометричними властивостями, які є предметом дослідження геометрії Евкліда. Пакет DG дозволяє виконувати геометричні побудови швидко і точно, швидко і точно виконувати перетворення фігур, вимірювати параметри отриманих геометричних динамічних рисунків (які ми будемо скорочено називати ДР). Параметри ДР можна динамічно змінювати (наприклад, перетягувати базові точки ДР на нові позиції), при цьому пакет буде автоматично (динамічно) обчислювати нові параметри рисунка і перебудовувати його. Це відкриває нові можливості дослідження геометричних фігур. Геометрія стає більш наочною, “експериментальною” — за допомогою пакета DG властивості геометричних фігур можна підмітити, після чого їх можна експериментально перевірити або спростувати.
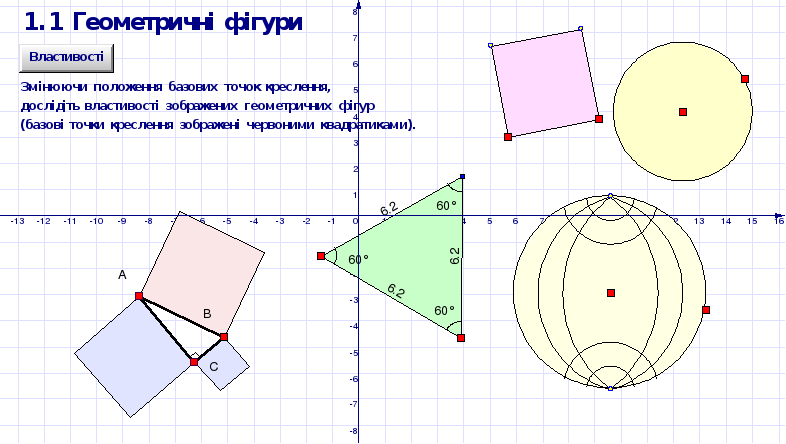
Рисунок 1.1 ДР “Геометричні фігури”
2. Точка і пряма
Розглянемо першу аксіому геометрії, яка характеризує властивості належності точок і прямих на площині. Після цього обговоримо особливості побудов точок і прямих у середовищі пакета DG.
Аксіома 1. Точка і пряма
Яка б не була пряма, існують точки, що належать цій прямій, і точки, що не належать їй.
Через будь-які дві точки можна провести пряму і тільки одну.
Для побудови точок у пакеті DG є інструмент Точка, який на панелі геометричних інструментів представлено кнопкою ![]() . Для вилучення точок можна скористатися контекстним меню точки, для чого треба підвести курсор миші до відповідної точки (при цьому курсор змінить свій вигляд) і клацнути правою кнопкою миші; потім зі спадаючого меню обрати команду Вилучити точку.
. Для вилучення точок можна скористатися контекстним меню точки, для чого треба підвести курсор миші до відповідної точки (при цьому курсор змінить свій вигляд) і клацнути правою кнопкою миші; потім зі спадаючого меню обрати команду Вилучити точку.
Завдання 2.1
Побудуйте на площині декілька точок, скориставшись інструментом Точка.
Вилучіть точки за допомогою команди Вилучити точку.
Для підвищення виразності рисунків зображення точок можна редагувати. Для цього треба скористатися контекстним меню точки й обрати в ньому команду Властивості точки. На рисунку 1.2 наведено зображення, яке побудовано виключно точками, з використанням різних елементів форматування.
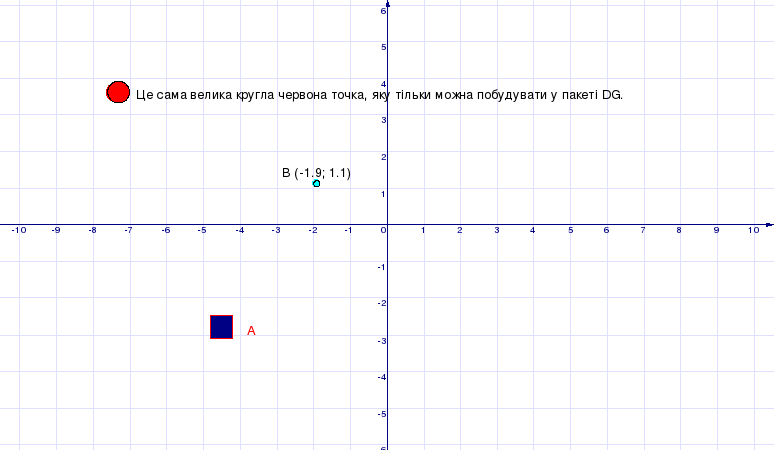
Рисунок 1. 2 ДР “Побудова та форматування точок у пакеті DG”
Завдання 2.2
Спробуйте самостійно повторити побудову ДР “Побудова та форматування точок у пакеті DG”.
Побудуйте в пакеті DG оригінальний динамічний рисунок за допомогою тільки одного примітиву Точка.
3. Відрізок
Розглянемо аксіому розміщення точок на прямій.
Аксіома 2. Розміщення точок на прямій
З трьох точок на прямій одна і тільки одна лежить між двома іншими.
У пакеті DG є спеціальний інструмент Точка фігури для побудови точки, яка належить геометричній фігурі (прямій, променю, відрізку, колу, дузі кола). Для його використання достатньо активізувати цей інструмент — натиснути на кнопку ![]() на панелі геометричних інструментів, або обрати команду Фігури\Точка\Точка фігури в головному меню пакета. Якщо тепер підвести курсор до геометричної фігури (прямої, променя, відрізка, кола, дуги кола), він змінить свій вигляд, а після натискування на кнопку миші на геометричній фігурі з’явиться точка. Побудована точка не буде вільною — її не можна перетягнути у довільну точку екрана за допомогою миші, вона завжди буде належати геометричній фігурі на якій її було сконструйовано. Але її можна переміщувати вздовж цієї геометричної фігури. Такі точки в пакеті DG називаються напівзалежними — вони мають тільки одну степінь свободи на відміну від вільних (або базових) точок, які можуть вільно переміщуватися на площині рисунка.
на панелі геометричних інструментів, або обрати команду Фігури\Точка\Точка фігури в головному меню пакета. Якщо тепер підвести курсор до геометричної фігури (прямої, променя, відрізка, кола, дуги кола), він змінить свій вигляд, а після натискування на кнопку миші на геометричній фігурі з’явиться точка. Побудована точка не буде вільною — її не можна перетягнути у довільну точку екрана за допомогою миші, вона завжди буде належати геометричній фігурі на якій її було сконструйовано. Але її можна переміщувати вздовж цієї геометричної фігури. Такі точки в пакеті DG називаються напівзалежними — вони мають тільки одну степінь свободи на відміну від вільних (або базових) точок, які можуть вільно переміщуватися на площині рисунка.
Завдання 3.1
Побудуйте в пакеті DG декілька прямих.
Побудуйте на прямих декілька точок, скориставшись для цього інструментом
 Точка фігури.
Точка фігури.Динамічно змінюючи параметри побудованих прямих та положення точок на них наочно переконайтеся, що аксіома 2 розміщення точок на прямій виконується для прямих та точок, побудованих у пакеті DG.
Зауваження
Точку можна пристебнути до фігури або відстебнути від фігури — властивість точки бути “пристебнутою” до геометричної фігури (бути напівзалежною точкою), можна змінити, перетворивши її на вільну точку. Для цього треба викликати контекстне меню “пристебнутої” точки, клацнувши на ній правою кнопкою миші, й у спадаючому меню обрати команду Відстебнути точку.
Навпаки, вільну точку можна перетворити у напівзалежну, пристебнувши її до фігури. Для цього також треба скористатися контекстним меню точки: підвести відповідну точку до геометричної фігури, після чого викликати контекстне меню точки й у спадаючому меню вибрати команду Пристебнути до фігури.
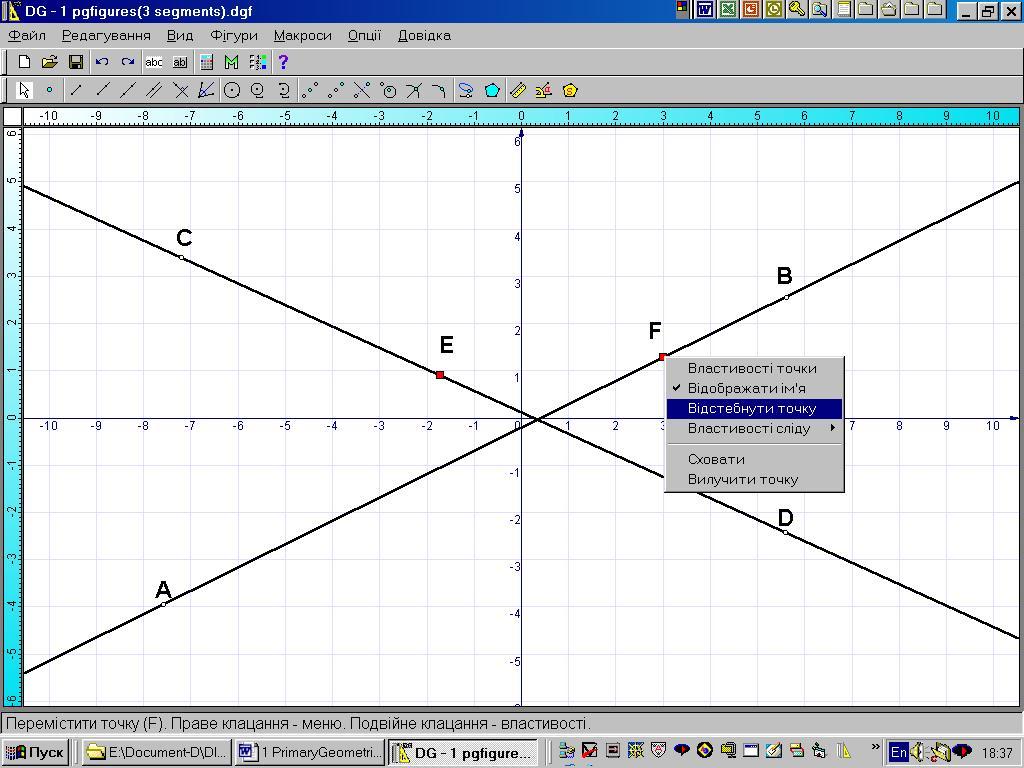
Рисунок 1. 3 ДР “Як відстебнути та пристебнути точку до прямої”
Завдання 3.2
На рисунку, який було підготовлено при виконанні завданні 3.1, відстебніть точки, що лежать на прямих (зрозуміло, базові точки прямих відстебнути від цих прямих неможливо).
Впевніться за допомогою експериментів, що відстебнуті точки перетворилися на вільні точки.
Знову пристебніть точки, що були відстебнуті, до прямих.
Впевніться за допомогою експериментів, що пристебнуті точки перетворилися в напівзалежні точки.
Крім прямої в пакеті DG є і інші прямолінійні примітиви:
Відрізок — його можна побудувати за допомогою відповідного інструмента
 Відрізок. Для побудови відрізка достатньо клацнути на точках — кінцях цього відрізка (при цьому кінцями відрізка можуть бути вільні точки, напівзалежні точки, залежні точки2; клацання мишкою на вільному місці створює нову вільну точку).
Відрізок. Для побудови відрізка достатньо клацнути на точках — кінцях цього відрізка (при цьому кінцями відрізка можуть бути вільні точки, напівзалежні точки, залежні точки2; клацання мишкою на вільному місці створює нову вільну точку). Промінь — його можна побудувати за допомогою інструмента
 Промінь. Для побудови променя достатньо клацнути на точках — початку променя та довільній точці на промені (як і у випадку з відрізком, базовими точками променя можуть бути вільні точки, напівзалежні точки, залежні точки; клацання мишкою на вільному місці створює нову вільну точку).
Промінь. Для побудови променя достатньо клацнути на точках — початку променя та довільній точці на промені (як і у випадку з відрізком, базовими точками променя можуть бути вільні точки, напівзалежні точки, залежні точки; клацання мишкою на вільному місці створює нову вільну точку).
4. Вимірювання відрізків
Аксіома 3. Вимірювання відрізків
Кожний відрізок має певну довжину, більшу від нуля. Довжина відрізка дорівнює сумі довжин частин, на які він розбивається будь-якою його точкою.
У пакеті DG є спеціальний інструмент
пакеті DG є спеціальний інструмент ![]() — Виміряти відстань для вимірювання довжин відрізків. Для вимірювання довжини відрізка достатньо клацнути мишкою на його кінцях; для вимірювання відстані між двома довільними точками (навіть якщо вони не з’єднані відрізком) достатньо клацнути на цих точках. Довжина відрізка відображається в надписі, який автоматично розміщується біля його середини. Місце надпису можна змінити, перетягуючи його за допомогою миші на нове місце. Для корегування форми представлення надпису треба скористатися його контекстним меню, яке можна викликати, клацнувши на ньому правою кнопкою миші. Точність вимірювань встановлюється в головному меню на вкладниці Опції\Опції\Різне (Рис. 1.4).
— Виміряти відстань для вимірювання довжин відрізків. Для вимірювання довжини відрізка достатньо клацнути мишкою на його кінцях; для вимірювання відстані між двома довільними точками (навіть якщо вони не з’єднані відрізком) достатньо клацнути на цих точках. Довжина відрізка відображається в надписі, який автоматично розміщується біля його середини. Місце надпису можна змінити, перетягуючи його за допомогою миші на нове місце. Для корегування форми представлення надпису треба скористатися його контекстним меню, яке можна викликати, клацнувши на ньому правою кнопкою миші. Точність вимірювань встановлюється в головному меню на вкладниці Опції\Опції\Різне (Рис. 1.4).
Завдання 4.1
Побудуйте новий рисунок, а на ньому — довільну пряму. На прямій поставте точку за допомогою інструмента
 Точка фігури.
Точка фігури. Виміряйте довжини трьох відрізків, які утворені побудованими трьома точками (дві точки — базові точки прямої і одна напівзалежна точка, що належить прямій).
Впевніться за допомогою експериментів, що аксіома вимірювання відрізків виконується в середовищі пакета DG. Для цього переміщуйте побудовані точки і спостерігайте за довжинами відрізків.
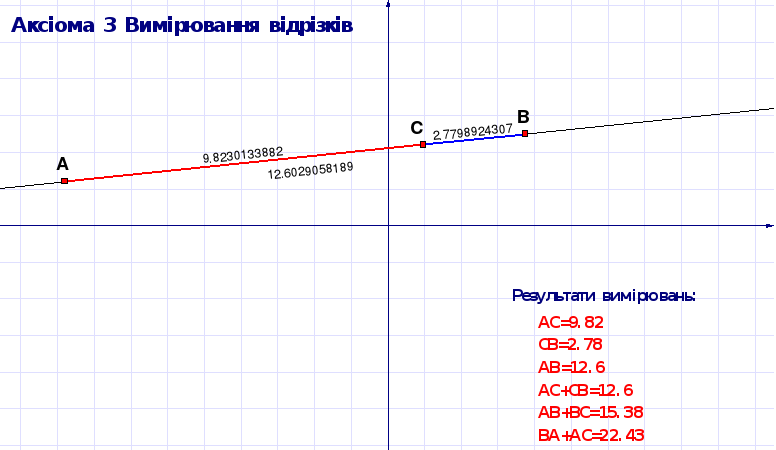
Рисунок 1. 5 ДР “Аксіома 3. Властивості вимірювання відрізків”
5. Півплощини
Аксіома 4. Розміщення точок відносно прямої на площині
Пряма розбиває площину на дві півплощини.
Якщо дві точки лежать в одній півплощині, на які розбиває площину деяка пряма, то відрізок, з кінцями в цих точках, не перетинає дану пряму. Якщо ж точки лежать в різних півплощинах, на які розбиває площину деяка пряма, то відрізок, з кінцями в цих точках, перетинає дану пряму.
Завдання 5.1
Побудуйте новий рисунок, а на ньому — довільну пряму.
Побудуйте довільний відрізок, кінці якого не лежать на прямій.
Впевніться за допомогою експериментів, що аксіома 4 розміщення точок відносно прямої на площині виконується у середовищі пакета DG. Для цього переміщуйте базові точки рисунка довільним чином і спостерігайте за виконанням аксіоми.
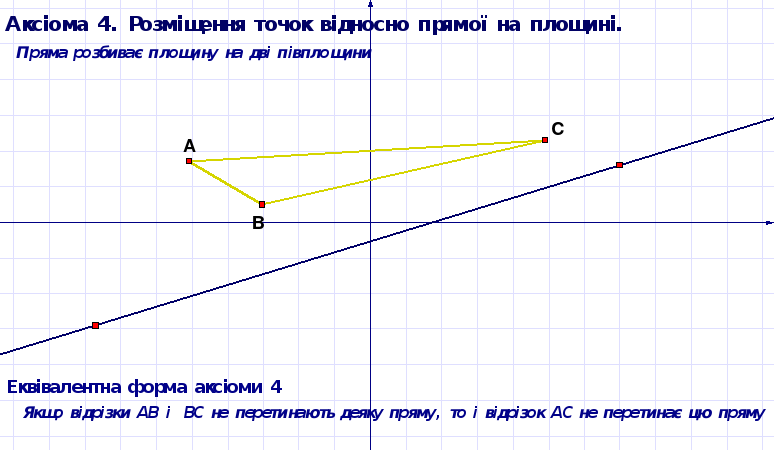
Рисунок 1.6 ДР “Аксіома 4. Розміщення точок відносно прямої на площині.”
6. Півпряма або промінь
Нагадаємо, що півпрямою або променем називають частину прямої, яка складається з усіх точок цієї прямої, що лежать по один бік від даної на ній точки; ця точка називається початковою точкою півпрямої. Різні півпрямі однієї й тієї ж прямої зі спільною початковою точкою називаються доповняльними.
Наведемо приклад використання променя при розв’язуванні задачі.
Задача 1.6.1
У площині дано многокутник F і довільну точка P, яка не належить жодній з його сторін. Як визначити, лежить точка P зовні чи всередині многокутника F?
Ця задачу можна розв’язувати різними способами, але найпростіший, мабуть, такий. Побудуємо довільний промінь, що виходить із точки P і порахуємо число точок перетину променя зі сторонами многокутника F. Якщо точок перетину буде непарне число, то точка P лежить всередині многокутника, якщо ж парне число — зовні многокутника. Особливі випадки мають місце коли промінь проходить через вершини многокутника. Самостійно вдоскональте запропоноване рішення для цих випадків.
Завдання 6.1
Побудуйте довільний многокутник, скориставшись для цього інструментом
 Многокутник. Зауважимо, що при побудові многокутника, після задання всіх його вершин потрібно повторно вказати його першу вершину.
Многокутник. Зауважимо, що при побудові многокутника, після задання всіх його вершин потрібно повторно вказати його першу вершину. Побудуйте довільний промінь, скориставшись для цього інструментом
 Промінь.
Промінь.За допомогою комп’ютерних експериментів підтвердіть або спростуйте висловлені вище гіпотези щодо умов, коли точка лежить зовні або всередині многокутника.
За допомогою комп’ютерних експериментів дослідіть особливі випадки — випадки, коли промінь проходить через вершину многокутника.
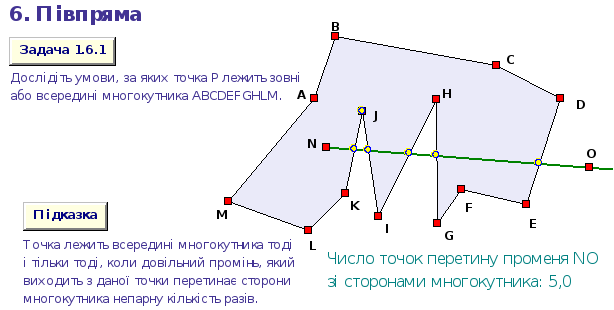
Рисунок 1. 7 ДР "Задача 1.6.1"
7. Кут
Згідно з підручником, кутом називається фігура, яка складається з точки — вершини кута і двох різних півпрямих, що виходять із цієї точки — сторін кута.
У пакеті DG немає примітива кут — його треба конструювати згідно з наведеним означенням: побудувати вершину кута, а потім за допомогою примітива Промінь побудувати дві сторони кута — дві півпрямі, що виходять з побудованої точки — вершини кута3.
Завдання 7.1
Побудуйте довільний кут.
Змінюючи положення базової точки сторони кута перетворіть побудований кут на гострий; тупий; прямий; розгорнутий.
Побудуйте точки на сторонах кута.
З’єднайте побудовані точки відрізком, скориставшись для цього інструментом Відрізок.
Побудуйте промінь, що проходить між сторонами кута.
8. Відкладання відрізків і кутів
Під час виконання побудов дуже часто виникає потреба відкладання відрізків даної довжини. Наступна аксіома віддзеркалює основну властивість цієї дії.
Аксіома 6. Відкладання відрізків
На будь-якій півпрямій від її початкової точки можна відкласти відрізок даної довжини і тільки один.
Для експериментальної перевірки справедливості цієї аксіоми достатньо побудувати промінь з початком у довільній точці A; на цьому промені побудувати за допомогою інструмента Точка фігури точку C; виміряти довжину відрізка AC, скориставшись інструментом Вимірювати відстань. Після цього, переміщуючи точку C вздовж променя, переконаємося, що довжина відрізка монотонно збільшується при віддаленні точки C від початку A і може набути будь-якого доданого значення. Зображення відповідного ДР “Аксіома 6. Відкладання відрізків” наведено нижче.
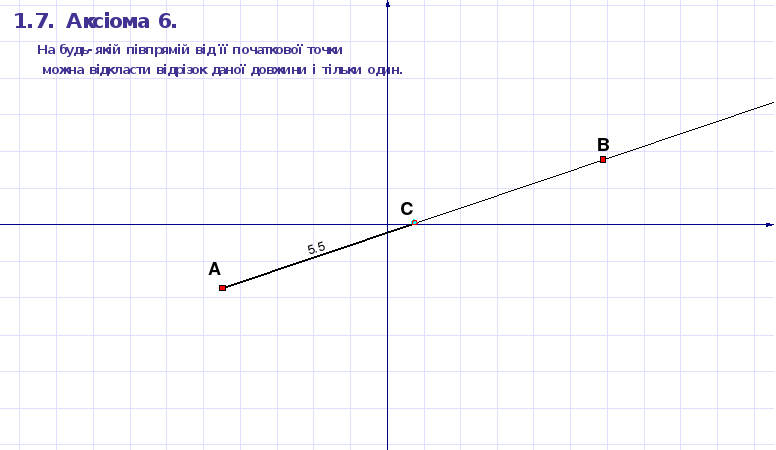
Рисунок 1. 8 “ Аксіома 6. Відкладання відрізків”
ДР "Аксіома 6. Відкладання відрізків" віддзеркалює процес відкладання на промені відрізка заданої довжини за допомогою лінійки. Якщо виникає потреба відкласти відрізок, довжина якого дорівнює довжині іншого відрізка, то можна виміряти довжину даного відрізка, а потім за допомогою лінійки відкласти відрізок отриманої довжини на промені. Це можна зробити більш ефективно (без зайвих дій вимірювання довжини відрізка) за допомогою циркуля. Виконайте такі побудови:
Побудуйте довільний відрізок, скориставшись інструментом Відрізок.
Побудуйте довільний промінь, скориставшись інструментом Промінь.
Побудуйте коло, радіус якого дорівнює довжині побудованого відрізка, а центр збігається з початком променя, скориставшись інструментом Коло за радіусом.
Побудуйте точку перетину побудованого кола і променя, скориставшись інструментом Точка перетину.
Виміряйте довжини обох відрізків і переконайтеся, що вони рівні, скориставшись інструментом Виміряти відстань.
Виконайте тестування розробленого ДР, змінюючи його параметри і спостерігаючи за довжинами відрізків.
На рисунку 1.9 наведено зображення відповідних побудов.
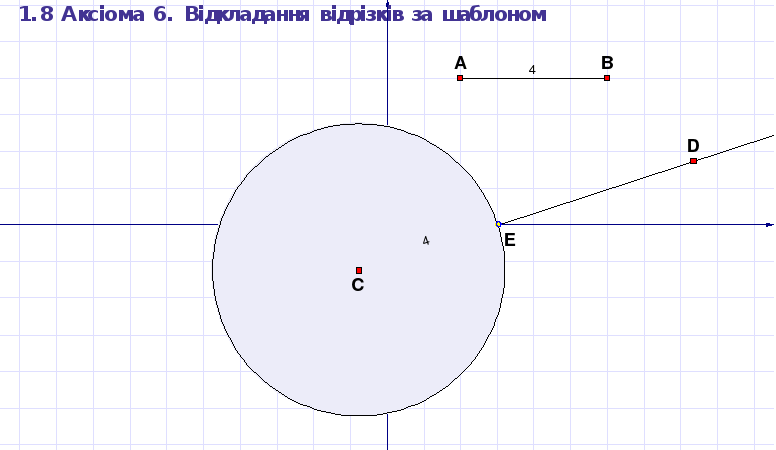
Рисунок 1. 9 ДР “Аксіома 6. Відкладання відрізків за шаблоном”
Відкладання відрізка за шаблоном цілком повторює операції відповідних побудов за допомогою звичайного циркуля.
Зауважимо також, що в пакеті DG є можливість створювати макроси — пойменовані (названі) процедури виконання заданих послідовностей дій. Можна створити макрос SegmentBySample, тоді зазначені побудови будуть виконуватися автоматично після задання вихідних параметрів — кінців відрізка та точок, які задають промінь.
Завдання 8.1
Почніть побудову нового ДР, скориставшись для цього командою Файл\Новий.
Завантажте макрос SegmentBySample з бібліотеки макросів, скориставшись для цього командою Макроси\Завантажити макрос.
Побудуйте довільний відрізок.
Побудуйте довільний промінь.
Відкладіть на промені відрізок, довжина якого дорівнює довжині заданого відрізка, скориставшись макросом SegmentBySample.
Аксіома 7 стосується відкладання кутів і відображає процес відкладання від променя кута заданої величини за допомогою транспортира.
Аксіома 7. Відкладання кута
Від будь-якої півпрямої у дану півплощину можна відкласти кут з даною градусною мірою, меншою за 180, і тільки один.
Неважко створити динамічний рисунок, який ілюструє це твердженню. Ми не будемо обговорювати деталі його побудови. Наведемо можливий варіант ДР “Аксіома 7. Відкладання кута” (Рис. 1.10).
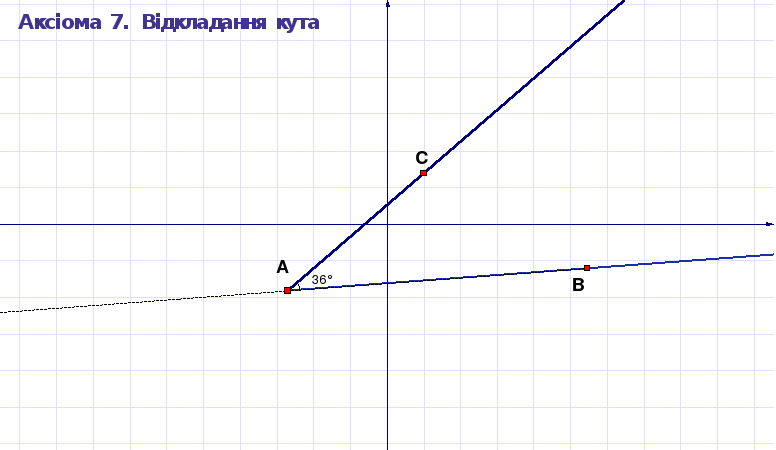
Рисунок 1. 10 ДР “Аксіома 7. Відкладання кута”
Як і у випадку відкладання відрізків, на практиці часто виникає потреба відкласти від даного променя в дану півплощину кут, градусна міра якого дорівнює градусній мірі деякому іншого кута. Якщо для цього використовувати транспортир, то спочатку треба виміряти величину заданого кута, а потім відкласти його відповідним чином від заданого променя. Відкладемо кут, рівний даному куту (тобто, кут, що має ту ж саму градусну міру), за допомогою циркуля.
Сконструюємо ДР “Відкладання кута за шаблоном”.
Побудуйте кут BAC, який відіграватиме роль шаблона. Для побудови скористайтеся інструментом Промінь.
Побудуйте промінь DE — промінь, від якого відкладатимуться кути.
Побудуйте коло радіусом AB з центром у точці D, скориставшись інструментом Коло за радіусом.
Знайдіть точку F перетину побудованого кола з променем DE, скориставшись інструментом Точка перетину.
Побудуйте коло радіусом BC з центром у точці F.
Побудуйте коло радіусом AC з вершиною в точці D.
Знайдіть точки H і I перетину кіл з центрами в точках F і D, скориставшись інструментом Точка перетину.
Виберіть з точок H і I ту, яка відповідає умовам задачі, і через неї проведіть промінь з початком у точці D.
Виміряйте кути, скориставшись інструментом Виміряти кут.
Виконайте тестування розробленого ДР — при зміні параметрів рисунка кути повинні залишатися рівними.
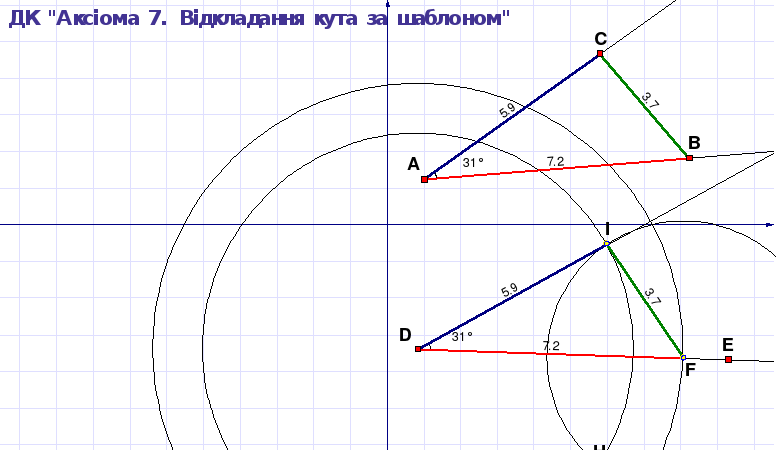
Рисунок 1. 11 ДР “Відкладання кута за шаблоном”
На динамічному рисунку ми зберегли всі допоміжні побудови і рівні відрізки зафарбували однаковим кольором. Експериментально переконайтеся, що побудови виконано правильно; акуратне доведення потребує використання властивостей трикутників, які будуть вивчатися в курсі геометрії пізніше (ознака рівності трикутників за трьома сторонами).
Можна також розробити макрос AngleBySample для побудови кута за шаблоном.
Завдання 8.2
Почніть побудову нового ДР, скориставшись кнопкою Створити новий рисунок, що розміщена на стандартній панелі інструментів.
Завантажте макрос AngleBySample з бібліотеки макросів, скориставшись командою Макроси\Завантажити макрос.
Побудуйте довільний кут.
Побудуйте довільний промінь.
Відкладіть від променя кут, градусна міра якого дорівнює градусній мірі даного кута, скориставшись макросом AngleBySample.
9. Трикутник
За означенням, трикутник є фігурою, що складається з трьох точок, що не лежать на одній прямій і трьох відрізків, які попарно сполучають ці точки.
На перший погляд здається все просто, але це не зовсім так. Кожна наука вивчає не властивості конкретних об’єктів своєї предметної області, а спільні властивості цілих класів об’єктів. Тому дуже важливим є критерій, коли об’єкти можна віднести до одного класу, в нашому випадку важливим є те, коли можна вважати два трикутника рівними.
Треба зрозуміти означення рівності трикутників. Наступна аксіома стверджує існування трикутника, що дорівнює даному, і який можна побудувати виходячи з довільного положення його вершини, довільного напряму його сторони, довільної півплощини, в якій він розташований. Таким чином, на площині можна побудувати безліч трикутників, рівних даному.
10. Існування трикутника, що дорівнює даному
Аксіома 8. Існування трикутника, що дорівнює даному
Який би не був трикутник, існує трикутник, що дорівнює йому у заданому розміщенні відносно даної півпрямої.
При побудові за шаблоном кута, рівного даному (п. 8), ми фактично будували трикутник, рівний даному, і який відкладено від даного променя в дану півплощину.
Зважаючи на важливість питання, ми повторимо ці побудови в наступному ДР “Аксіома 8. Існування трикутника, що дорівнює даному”.
Побудуйте довільний трикутник ABC, скориставшись інструментом
 Многокутник.
Многокутник.Побудуйте довільний промінь DE, скориставшись інструментом Промінь.
Відкладіть на промені DE відрізок, що дорівнює стороні AB трикутника:
Побудуйте коло з радіусом AB і центром у точці D, скориставшись інструментом Коло за радіусом.
Знайдіть точку F перетину променя DE з побудованим колом, скориставшись інструментом Точка перетину.
Побудуйте коло з радіусом AC і центром у точці D.
Побудуйте коло з радіусом BC з центром у точці F.
Знайдіть точки перетину H і I кіл з центрами в точках D і F.
Побудуйте трикутники DFI і DFH, скориставшись інструментом
 Многокутник.
Многокутник.Виконайте вимірювання сторін трикутників, скориставшись інструментом Виміряти відстань.
Виконайте вимірювання кутів трикутників, скориставшись інструментом Виміряти кут.
Трикутники DFG і DFI — шукані; кожен з них лежить в одній з двох півплощин, які визначаються заданим променем. Наведемо варіант відповідного ДР (Рис. 1.12).
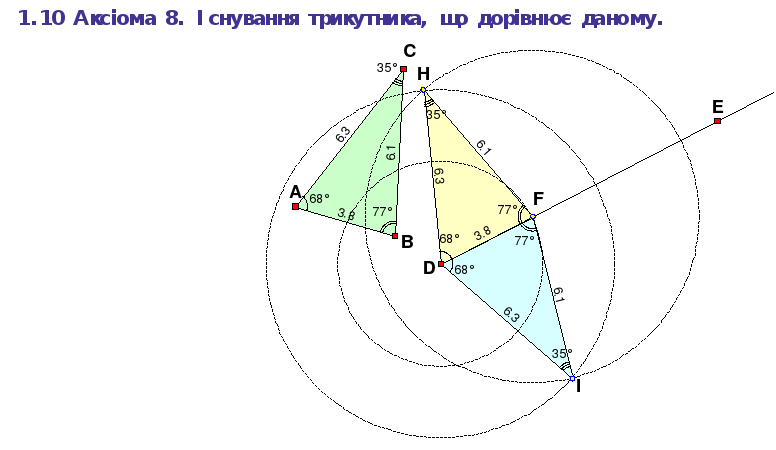
Рисунок 1. 12 ДР “Аксіома 8. Існування трикутника, що дорівнює даному”
Завдання 10.1
За допомогою комп’ютерних експериментів впевніться, що трикутники DFI і DFH — шукані, тобто рівні вихідному трикутнику ABC.
11. Паралельні прямі
Аксіома 9. Паралельні прямі
Через точку, що не лежить на даній прямій, можна провести на площині не більше як одну пряму, паралельну даній.
Для побудови прямої, яка проходить через дану точку паралельно до даної прямої, в пакеті DG існує спеціальний інструмент ![]() Паралельна пряма.
Паралельна пряма.
Побудуємо ДР “Паралельні прямі”:
Побудуємо довільну пряму AB, скориставшись інструментом Пряма.
Побудуємо довільну точку C, скориставшись інструментом Точка.
Через точку C проведемо пряму, паралельну прямій AB, скориставшись інструментом Паралельна пряма.
Завдання 11.1
Змінюючи масштаб зображення, переконайтеся, що побудовані прямі не перетинаються (збільшення масштабу виконується натискуванням на клавішу на цифровій клавіатурі, зменшення — натискуванням на клавішу ). Зазначені операції можна повторювати до 32 разів.
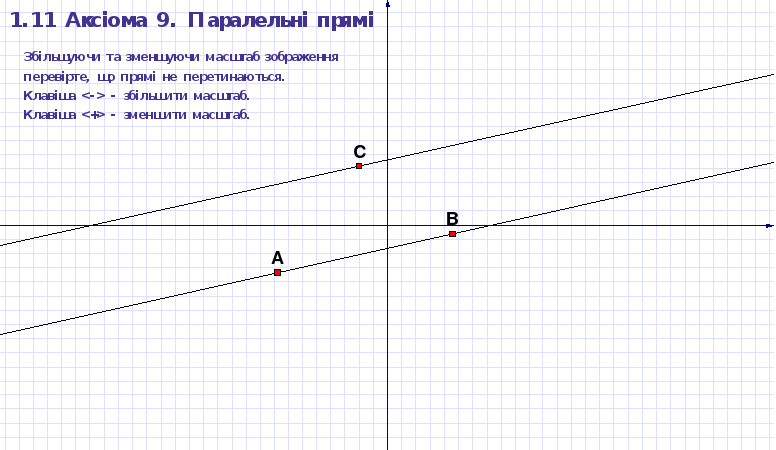
Рисунок 1. 13 ДР “Паралельні прямі”
Зауважимо, що під час проведення комп’ютерних експериментів у середовищі пакета DG постійно виникає потреба спостерігати ті чи інші фрагменти рисунка. Пересування вздовж площини виконується в ручному режимі — для цього слід виконати операцію Drag and Drop на полі рисунка (натиснути на ліву кнопку миші і, не відпускаючи її, змістити мишу у відповідному напрямку).
12. Теореми і доведення
Чи може допомогти пакет DG у доведенні теорем? На перший погляд — ні, тому, що у теоремах говориться про справедливість деякого твердження (висновку теореми) для нескінченої множини об’єктів (тих об’єктів, що задовольняють умову теореми). За допомогою пакета DG можна тільки експериментально перевірити справедливість висновку теореми для великої кількості об’єктів, які задовольняють умову теореми, причому, цю перевірку можна зробити за допомогою пакета DG значно точніше, ніж без нього, але й тільки, як сказав Мцирі з однойменної поеми М.Ю. Лермонтова при аналізі причин втечі з монастиря4. До того ж перевірку можна виконати тільки наближено — всі обчислення в пакеті виконуються наближено. Наприклад, довжину діагоналі квадрата зі стороною 1 можна обчислити тільки наближено, оскільки DG може оперувати тільки десятковими дробами з певного діапазону. З тієї ж самої причини довжину третини одиничного відрізка буде обчислено наближено — число 1/3 не можна точно представити у вигляді скінченого десяткового дробу. Проблему наближеності обчислень можна буде усунути у майбутньому, наділивши пакет можливостями виконання точних обчислень, як у пакетах комп’ютерної алгебри (наприклад, у пакеті Derive). Проблему експериментальних досліджень властивостей нескінченої кількості об’єктів, що задовольняють умові теореми, не можна буде розв’язати ніколи. Разом із тим, проводити бездоганні з математичної точки зору доведення теорем можна аналітично, за допомогою символьних обчислень, наприклад, у середовищі пакета Derive. Таким чином, принципові розв’язання питань автоматизації доведень можливі тільки на шляху використання пакетів символьних перетворень. Залишимо поки доведення теорем дослідникові, принаймні у курсі геометрії загальноосвітньої школи. А навіщо тоді пакет DG з його можливостями автоматизації наближених експериментів в геометрії? Навіщо експерименти в геометрії? Чи можуть допомогти експерименти під час доведення теорем? За суттю, весь даний посібник є докладною відповіддю на ці запитання. Оскільки даний параграф присвячений питанню доведення теорем, сформулюємо, як можна використовувати пакет DG у процесі доведення теорем.
Побудова контрприкладу до теореми за допомогою пакета DG
Звідки беруться теореми? Теореми — це результат математичного передбачення дослідника. Попередньо невідомо: це передбачення є істинним чи хибним. В першому випадку гіпотезу можна довести, а в другому — спростувати. В першому випадку теорему доводять за допомогою логіки, як говорять, дедуктивно, в другому випадку — вдаються до побудови приклада об’єкта, для якого твердження не виконується. Процес пошуку доведення теореми невід’ємний від процесу пошуку контрприкладів до теореми. Пакет DG можна ефективно використовувати для спростування хибних тверджень, хибних гіпотез.
Як приклад використання пакета DG з метою спростування хибних гіпотез розглянемо ДР “Задача про ворону та сир” (умова задачі наведена на рисунку 1.14).
У процесі розв’язування задачі можуть виникнути гіпотези, що оптимальною точкою буде:
1) точка, яка рівновіддалена від основи паркана і основи дерева;
2) точка, яка рівновіддалена від вершини паркана і вершини дерева.
Завдання 12.1
За допомогою експериментів із залученням ДР “Задача про ворону та сир” спростуйте наведені вище гіпотези.
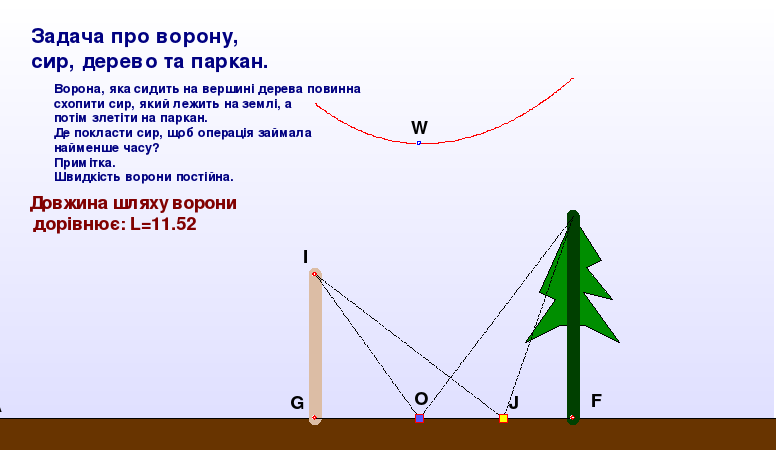
Рисунок 1.14 ДР “Задача про ворону та сир”
Пошук закономірностей за допомогою пакета DG
Доведення теореми звичайно розбивається на окремі кроки — твердження, які теж є теоремами, але більш простими — образно кажучи, теоремами-одноходівками, які є логічними наслідками співставлення деякої умови і вже доведеної раніше теореми або аксіомами геометрії, які вважаються істинними за визначенням. Уміння побачити ці кроки доведення — більш прості теореми, послідовність яких і складає доведення теореми, є мистецтво математика. Пакет DG можна використовувати для пошуку закономірностей, послідовність яких може привести до доведення теореми.
Ці закономірності, висловлені у формі гіпотез, також потребують дедуктивного доведення. Разом із тим, правильно сформульоване питання є половиною відповіді на нього. Видатний філософ сучасності М. Хайдегер говорить, що філософія (тобто “любомудріє”) є вміння ставити запитання. Те ж саме можна сказати про математику, тим більше, що математика займає проміжне положення між конкретними науками і філософією, математика — це мова науки (як сказав великий І. Ньютон: “Природа розмовляє з людиною мовою математики”).
Як приклад використання пакета DG з метою знаходження закономірностей є ДР “Задача про ворону та сир”.
У цій задачі мабуть “більше ніж половиною розв’язання” є здогадка про те, що шукана точка задовольняє таку умову: відрізки, які сполучають її з вершиною дерева й точкою на паркані, утворюють рівні кути з горизонтальною прямою. Відшукання цієї гіпотези спрощується за допомогою наведеного ДР. Усі параметри ДР можна змінювати — висоту дерева, висоту паркана, положення дерева, паркана та сиру, причому довжина шляху ворони автоматично перераховується під час змін ДР. Експерименти допоможуть висловити ґрунтовну гіпотезу, після чого тільки й можна приступати до доведення або спростування цієї гіпотези. Доведення цього твердження спирається на властивості точок, симетричних відносно прямої (вони рівновіддалені від довільної точки осі симетрії) і на властивості сторін трикутника (сума довжин двох довільних сторін трикутника більша довжини його третьої сторони). Ці твердження будуть доведені в курсі геометрії пізніше.
13. Аксіоми
Як зазначалося в попередньому пункті, всі властивості геометричних фігур повинні бути доведені за допомогою логічних міркувань (дедукції). При цьому більш складні твердження зводять до більш простих, більш прості зводять до ще більше простих і т.д. Однак зрозуміло, що на цьому шляху повинна бути межа — інакше доведення ніколи не закінчиться. Таким чином, повинні існувати деякі твердження (аксіоми), істинність яких не буде доводитись, вони будуть істинними з інших міркувань. Найпростіший вихід — поступити формально, прийняти деякі властивості істинними “за означенням” або “за домовленістю”. Це логічно бездоганний підхід, проте з точки зору практичної значущості теорії, незрозуміло, чи може така теорія бути корисною на практиці. Тобто аксіоми повинні якоюсь мірою відбивати властивості реального світу. Призначенням геометрії є моделювання просторових властивостей світу, тому аксіоми геометрії повинні відбивати просторові властивості світу — бути абстракціями реальних об’єктів і їх властивостей. Геометрія в перекладі з грецької означає “землемірство”. Площину можна собі уявляти як рівнинну місцевість, на якій виконуються побудови за допомогою інструмента “геошнур” — двох кілків, сполучених шнурком. Ввіткнення кілка в землю відповідає побудові точки на площині, а натягування шнурка між двома кілками — проведенню прямої через дві точки. Обертання ж одного кілка навколо ввіткнутого в землю другого при натягнутому шнурку постійної довжини представляє побудову кола. За допомогою геошнура можна виконувати розмітку садибної ділянки.
Історично аксіоми геометрії відбивали властивості побудов на рівнинній поверхні за допомогою геошнура. І саме це забезпечило велику практичну значимість геометрії, бо геометрія є моделлю побудов на рівнині. З іншого боку, побудови на рівнині за допомогою геошнура виконують роль інтерпретації для геометрії — всі отримані в геометрії результати можуть бути використані на практиці відповідним чином.
Універсальність аксіоматичного методу виявляється в тому, що інтерпретацій аксіоматичних теорій може бути багато. Якщо для якоїсь множини об’єктів виконуються аксіоми теорії, то для цих об’єктів справедливі всі результати (теореми), що були отримані у межах цієї теорії.
Однією з інтерпретацій геометрій є побудови на папері за допомогою циркуля і лінійки.
Пакет DG — це ще одна інтерпретація геометрії Евкліда, геометрії на площині. Важливо усвідомити, що властивості точок, прямих та площин з точки зору математичної теорії і властивості цих об’єктів в пакеті DG не можна ототожнювати. Та ж сама ситуація, як і з побудовами на місцевості за допомогою геошнура чи побудовами на папері за допомогою циркуля та лінійки: точки, побудовані на аркуші паперу — це не точки у строгому розумінні терміну точка, прямі — не прямі, і площини — не площини. Разом із тим, пакет DG — інтерпретація геометрії на площині і це означає, що він моделює і з деякою похибкою відбиває відповідні властивості справжньої — абстрактної геометрії. Зразу ж зауважимо, що якість електронної моделі геометрії (пакета DG) значно вище за традиційні (побудови на місцевості, або на папері), проте й електронна модель є теж наближеною і цього не треба ні забувати, ні нехтувати цим. Найголовніше, що треба мати на увазі — це те, що пакет DG просто зручний інструмент для виконання геометричних побудов, деякою мірою, він є просто ”комп’ютерним інструментарієм геометрії” — “комп’ютерним олівцем”, “комп’ютерною лінійкою”, “комп’ютерним циркулем”.
Пакет DG — це магічні олівець, лінійка і циркуль, які працюють з магічною швидкістю, точністю, виразністю:
Магічна швидкість — обчислювальні потужності одного комп’ютера перевищують обчислювальні потужності всього людства разом, причому обчислення виконуються з абсолютною точністю (на відміну від людських обчислень);
Магічна точність — більше 10 значущих цифр (еквівалентна можливості виміряти відстань від Харкова до Києва з точністю до 0,1 міліметра):
Магічна виразність — графічні можливості комп’ютерів дозволяють використовувати палітру з більш ніж 16 000 000 кольорів (таку палітру, мабуть, не могли собі уявити і імпресіоністи).
Проте, крім магічних швидкості, точності та виразності, є ще дві магії пакета DG — це магія динамізму та магія інтелектуальності, які перетворюють його у принципово новий інструмент, який не можна реалізувати тільки комп’ютерними засобами.
Магічна динамічність. Пакет DG це не простий графічний редактор, який запам’ятовує графічні образи, це геометричний редактор, що запам’ятовує правила, алгоритми побудови графічних зображень, і тому при інтерактивній зміні положення базових точок зображення автоматично перебудовує зображення за збереженими правилами. Наприклад, якщо побудувати трикутник, а потім навколо нього описати коло, то під час переміщення вершин трикутника за допомогою миші коло автоматично буде змінюватись, залишаючись при цьому колом, яке описане навколо трикутника.
Магічна інтелектуальність. Пакет DG здатен накопичувати задачі, які він може розв’язувати самостійно (тобто, автоматично, без втручання користувача). Як відомо, один із найважливіших критеріїв інтелектуальності є вміння вчитись. Кожний користувач може навчити пакет DG розв’язувати типові задачі, які є особистісно значущими для нього. Для цього в DG умонтовано механізм розробки та використання макроконструкцій5.
Ми так багато сказали про магічні властивості пакета DG, проте не відповіли на головне питання — а навіщо він потрібний взагалі? Є геометрія — чудова наука, яка існує вже принаймні 2500 років, є сталий курс геометрії, сталі прийоми її викладання та вивчення. Що ще потрібно? Спробуємо відповісти на це питання. Найкращий метод навчання — самостійне відкриття закономірностей, відкриття, яке повторює шлях людства в опануванні знаннями. Це найкращий шлях, але і найтрудомісткіший — кожен учень повинен побути хоч трошки і Евклідом, і Архімедом, і Паскалем, і Ньютоном, і Менделєєвим, і Ейнштейном, і Ландау, .... Без сучасних потужних інформаційних технологій це завдання не розв’язати. За допомогою відповідних пакетів можна змоделювати умови, в яких відбулося відкриття, а учень сам, проводячи відповідну навчальну дослідницьку роботу, “відкриє” закономірності. При такому підході учень буде брати участь у відкритті властивостей, познайомиться з “технологією відкриття”, технологією “життя”, функціонування відповідної галузі науки. За допомогою пакета DG учень отримує зручний інструмент для проведення комп’ютерних експериментів у галузі геометрії.
Останнє важливе питання — виконання аксіом геометрії у пакеті DG. Коли експериментально перевіряємо справедливість аксіом у пакеті DG (наприклад, що через точку, яка не лежить на даній прямій, можна провести на екрані за допомогою пакета DG не більше як одну пряму, паралельну даній), ми тим самим перевіряємо, що система аксіом геометрії має інтерпретацію і тому геометрія є змістовною — її результати можна використовувати на практиці, принаймні в комп’ютерній геометрії. Проте кожна інтерпретація геометрії, у тому числі й комп’ютерна, дає можливість не тільки застосовувати отримані результати в галузі геометрії, але й допомагати в пошуку нових результатів. Розв’язуючи задачу, стародавній математик створював геометричний рисунок паличкою на піску, математик доінформаційного суспільства виконував побудови олівцем на папері, сучасний математик будує й досліджує геометричні моделі на екрані комп’ютера. Ці комп’ютерні моделі з одного боку можуть виконувати роль інтерпретацій відомих теорем геометрії, з другого боку — комп’ютерні моделі можуть виконувати роль джерела плідних ідей для відкриття нових властивостей геометричних фігур — нових теорем.
Аксіоми геометрії виникли з людського досвіду побудов на площині. Зрозуміло, в реальності не існує площини — нескінченної “абсолютно рівної” поверхні, яка не має “товщини”, на якій розташовані прямі — лінії, що не мають “ширини” і які “абсолютно прямі”, у площині та на прямих лежать точки — деякі ефемерні об’єкти, що не мають ані товщини, ані ширини, ані довжини.
Не існує в реальності ні прямих, ні точок. Навіщо ж вивчати властивості об’єктів, яких у реальності не існує? Відповідь і проста і складна: вивчати — для того, щоб знати, бо знання можуть бути тільки абстрактними, загальними, притаманними не тільки одному реальному об’єкту, а цілому класу реальних об’єктів. Це дуже складний процес формування абстрактних понять, і чим більше розвивається суспільство, тим більш загальні абстракції формуються, тим більш загальні теорії будуються. Математика — це універсальний інструмент для побудови моделей дійсності. Геометрія — це важливий розділ математики, який дозволяє в абстрактній формі моделювати та досліджувати просторові властивості об’єктів та процесів реального світу. Наприклад, в геометрії досліджено властивості площини, й отримані результати використовують архітектори, проектувальники, будівельники тоді, коли розглядається досить мала ділянка земної поверхні. Якщо ж вивчаються об’єкти, які розташовано на поверхні Землі і які мають досить великі розміри, то використовують розділ геометрії, який вивчає властивості сфери. Оскільки поверхні планет можна з великою точністю вважати сферами, то фахівці всіх спеціальностей, пов’язаних з розміщенням об’єктів на поверхні планет (геологи, геодезисти, машиністи, капітани, льотчики, космонавти і т.д.) можуть використовувати результати, які отримані відповідних розділах геометрії.
Для застосування результатів евклідової геометрії на практиці треба знайти ті об’єкти дійсності, які можна вважати за площини, прямі та точки і потім до них застосовувати результати, що отримані в геометрії.
1 Точне визначення руху фігур буде дано далі у курсі геометрії; образно-інтуїтивною мовою рухом фігури називається зміна положення фігури як “жорсткої конструкції”, тобто таке перетворення фігури, при якому не змінюються відстані між її точками. Аналогічно, масштабування фігури (геометричною мовою – подібність) образно-інтуїтивною мовою означає “рівномірне розтягування” або “рівномірний стиск” фігури, тобто таке перетворення, при якому відстані між точками змінюються в одну й ту саму кількість разів.
2 Залежна точка — це точка, яка не має степенів свободи — вона повністю визначається положенням інших точок (наприклад, точка перетину двох прямих). Докладніше про різновиди точок DG йдеться далі.
3 Використовуючи механізм макросів пакета DG, легко побудувати макрос Кут, тоді побудова кута буде зводитись до вибору макроса і клацанням мишею на трьох точках, які визначають кут. Допитливі можуть самостійно розібратися в механізмі роботи макросів. Докладне обговорення цього питання передбачено далі.
4 “Бежал я долго — где, куда?
Не знаю! Ни одна звезда
Не озаряла трудный путь.
Мне было весело вдохнуть
В мою измученную грудь
Ночную свежесть тех лесов,
И только!”
Ми теж, за прикладом Мцирі, хотіли б втекти від скучних побудов традиційних математичних курсів до живої математики, сповненої здогадок, помилок і відкриттів — “колізії ідей”, як охарактеризував стрижень свого життя найбільш відомий вчений 20 сторіччя Альберт Ейнштейн.
5 Макроконструкція (або просто макрос) — послідовність команд для виконавця (у нашому випадку — для пакета DG), яка виконується автоматично після виклику макросу і задання його вихідних параметрів.
24
Просмотр содержимого документа
«02 Adjacent & Vertical angles»
14. Суміжні кути
Н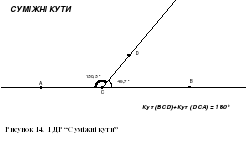 агадаємо, що два кути називаються суміжними, якщо в них одна сторона спільна, а дві інші сторони є доповняльними півпрямими.
агадаємо, що два кути називаються суміжними, якщо в них одна сторона спільна, а дві інші сторони є доповняльними півпрямими.
Завдання 14.1
Побудуйте в пакеті DG суміжні кути. Використовуючи інструмент Виміряти кут, знайдіть їх градусні міри. Яку гіпотезу відносно суми суміжних кутів можна висунути П ? Перевірте гіпотезу, використовуючи динамічні властивості побудованого рисунка. Для зручності доповніть рисунок динамічним надписом, який відображає суму кутів П . Спробуйте довести гіпотезу про суму суміжних кутів самостійно або скористайтеся підручником (Теорема 2.1).
З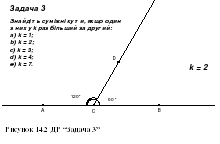 авдання 14.2
авдання 14.2
Побудуйте в пакеті DG динамічний рисунок для розв’язування задачі 3 (§ 2):
Знайдіть суміжні кути, якщо один з них у два рази більший за другий.
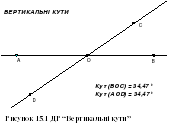
15. Вертикальні кути
Два кути називаються вертикальними, якщо сторони одного кута є доповняльними півпрямими сторін другого кута.
Завдання 15.1
Побудуйте в пакеті DG вертикальні кути. Порівняйте їх градусні міри. Яку гіпотезу відносно градусних мір вертикальних кутів можна висунути П ? Динамічно змінюючи один із вертикальних кутів, перевірте сформульовану вами гіпотезу. Якщо динамічні експерименти підтверджують гіпотезу, то спробуйте довести її самостійно або скористайтеся підручником (Теорема 2.2).
16. Перпендикулярні прямі
Для побудови прямої, перпендикулярної до даної прямої, в пакеті DG є інструмент Перпендикулярна пряма.
З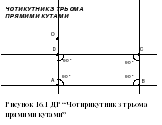 авдання 16.1
авдання 16.1
Використовуючи інструмент Перпендикулярна пряма, побудуйте чотирикутник ABCD, у якого кути A, B і C прямі П . Виміряйте кут D. Яку гіпотезу відносно градусної міри кута D можна висунути? Перевірте, чи залишається ваша гіпотеза справедливою при зміні параметрів чотирикутника.
17. Доведення від супротивного
Чи може допомогти пакет DG при доведенні від супротивного? Нагадаємо, що при доведенні геометричного твердження способом від супротивного спочатку робимо припущення, протилежне твердженню, яке треба довести. Потім, спираючись на аксіоми і раніше доведені теореми, показуємо, що наше припущення приводить до твердження, яке суперечить або умові теореми, або одній з аксіом, або вже доведеній теоремі. Отже, наше припущення було неправильним, що й доводить розглядуване твердження.
Таким чином, все доведення від супротивного грунтується на логічних міркуваннях. Зазначимо, що навіть рисунок, який ілюструє доведення, не завжди можна побудувати. Конфігурація, властивості якої досліджуються в процесі доведення, може взагалі не існувати. Це дало підставу назвати геометрію мистецтвом правильно міркувати на неправильних рисунках.
Але зазначимо, що теорему не достатньо довести дедуктивно, тобто спираючись на аксіоми і раніше доведені теореми. Теорему потрібно зрозуміти, проникнуть в неї. Твердження, яке ви збираєтесь доводити повинно бути інтуїтивно зрозумілим. Ви повинні бути психологічно готовими до сприйняття доведення. А найкращий шлях до цього лежить через відкриття геометричного твердження в процесі експериментальної роботи в середовищі пакета динамічної геометрії.
18. Бісектриса кута
Бісектрисою кута називається промінь з початком у вершині кута, який проходить між його сторонами і ділить кут пополам.
Для побудови прямої, що містить бісектрису кута, в пакеті DG є інструмент Бісектриса кута. Якщо ж ви хочете замість прямої, що містить бісектрису кута, будувати власне бісектрису, то скористайтеся макросом Bisector.DGM. Макроси в пакеті DG — це інструменти для геометричних побудов, які створені користувачем. Створення макросів вимагає від користувача вміння виконувати геометричні побудови. Але використовувати раніше створені макроси так же просто як і застосовувати стандартні інструменти пакета DG. Потрібно лише завантажити відповідні макроси. Макрос Bisector.DGM зберігається в папці 02 Adjacent & Vertical angles (DGM). Для його завантаження скористайтеся командою Макроси\Завантажити макрос. За допомогою діалогового вікна Відкрити знайдіть папку 02 Adjacent & Vertical angles (DGM), та двічі клацніть мишею на файлі Bisector.DGM. Після цього в розділі меню Макроси з’явиться команда Bisector.
19. Що потрібно робити, щоб добре встигати з геометрії
В підручнику геометрії наведено корисні поради з цього питання. Але в ті часи, коли вони були написані, ще не існувало комп’ютерних пакетів динамічної геометрії. Сьогодні варто доповнити ці поради ще однією:
Вивчайте геометрію з пакетом динамічної геометрії DG
П Сума суміжних кутів дорівнює 180.
ідказки
Вертикальні кути рівні.
Для створення динамічного надпису скористайтеся командою Редагування | Добавити надпис. В текстовому полі діалогового вікна введіть текст: Кут(BCD) + Кут(DCA) = [ANG(B, C, D) + ANG(D, C, A)]° .
Зауваження
Функція ANG(B, C, D) повертає величину кута BCD.
Значок градуса у виразі ANG(B, C, D) означає, що функція ANG(B, C, D) буде повертати градусну міру кута BCD.
Вираз в квадратних дужках буде автоматично обчислюватись при зміні положення точок A, B, C, D.
Для спрощення роботи при створенні динамічного виразу натисніть кнопку Вставити формулу … . Після цього можна скористатися графічним калькулятором. Наприклад, замість того щоб у текстовому полі набрати з клавіатури вираз ANG(B, C, D), натисніть на кнопку із зображенням трикутника, що розташована справа від кнопки Angle, та вкажіть точки B, C і D.
Побудова чотирикутника ABCD:
Будуємо довільну пряму OA (інструмент
 ).
).Через точку A проводимо пряму, перпендикулярну до прямої OA (інструмент
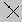 ).
).На побудованій прямій відмічаємо довільну точку B (інструмент
 ).
).Будуємо пряму BC, перпендикулярну до прямої AB.
Будуємо пряму, перпендикулярну до прямої BC, і знаходимо точку D перетину побудованої прямої з прямою OA (інструмент
 ).
).
Просмотр содержимого документа
«03 Triangle Test of equality»
Трикутники ABC і A1B1C1 називаються рівними, якщо AB = A1B1, AC = A1C1, BC = B1C1, A = A1, B = B1, C = C1. Отже, щоб довести рівність двох трикутників, користуючись означенням, ми повинні перевірити істинність шести рівностей. Виникає питання, а чи не можна для доведення рівності трикутників обмежитись перевіркою тільки деяких із наведених в означенні умов. Пошуку відповіді на поставлене питання і присвячено цей параграф.
20. Перша ознака рівності трикутників
Завдання 20.1
Д
ослідіть за допомогою ДР “Перша ознака рівності трикутників”, чи будуть рівними трикутники ABC і A1B1C1, якщо AB = A1B1, AC = A1C1, BAC = A1B1C1. (На динамічному рисунку вершини B1 і C1 трикутника A1B1C1 лежать на колах з центром A1, радіуси яких дорівнюють сторонам AB і AC відповідно. Таким чином, при будь-якому положенні початкових об’єктів AB = A1B1, AC = A1C1.)
Дослідження можна провести за такою схемою:
Задайте параметри трикутника ABC, переміщуючи його вершини (при цьому сторони A1B1 і A1C1 будуть залишатися рівними сторонам AB і AC відповідно).
Переміщуючи точку B1 (або C1), знайдіть таке її положення, щоб кут A1B1C1 став рівним куту ABC.
Порівняйте сторони та кути трикутника ABC з відповідними сторонами та відповідними кутами трикутника A1B1C1 (довжини сторін BC, B1C1 і градусні міри кутів ABC, A1B1C1, BCA і B1C1A1 відображаються на динамічному надписі).
Подумайте та перевірте, чи не можуть бути рівними кути A1B1C1 і ABC при іншому положенні точки B1.
Яку гіпотезу можна висунути в результаті ваших спостережень П ?
Перевірте вашу гіпотезу для трикутника ABC іншої форми та розмірів.
Порівняйте вашу гіпотезу з теоремою 3.1 підручника.
21. Використання аксіом при доведенні теорем
В попередньому пункті в результаті комп’ютерних експериментів ми відкрили першу ознаку рівності трикутників: якщо дві сторони і кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними другого трикутника, то такі трикутники рівні. Ми перевірили, що це твердження справедливе для багатьох трикутників і в нас майже не залишилося сумнівів, що воно справедливе завжди. І все ж таки твердження залишається не доведеним. По-перше, довжини сторін і градусні міри кутів обчислювалися наближено. По-друге, можливо твердження не виконується в деяких окремих випадках. Отже, теорему треба довести шляхом логічних міркувань. При цьому дозволяється користуватися лише аксіомами і раніше доведеними теоремами.
Зверніться до підручника і ще раз уважно розгляньте доведення теореми 3.1.
22. Друга ознака рівності трикутників
Завдання 22.1
Дослідіть за допомогою ДР “Друга ознака рівності трикутників”, чи будуть рівними трикутники ABC і A1B1C1, якщо AB = A1B1, BAC = B1A1C1, CBA = C1B1A1. (На динамічному рисунку вершина B1 трикутника A1B1C1 лежать на колі з центром A1, радіус якого дорівнює стороні AB. Таким чином, при будь-якому положенні початкових об’єктів AB = A1B1. Вершина C1 лежить на промені A1D).
Дослідження можна провести за такою схемою:
Задайте параметри трикутника ABC, переміщуючи його вершини (при цьому сторони A1B1 і AB будуть залишатися рівними).
Переміщуючи точку D, знайдіть таке її положення, щоб кут B1A1C1 став рівним куту BAC.
Переміщуючи тепер точку C1 вздовж променя A1D знайдіть таке її положення, щоб кут C1B1A1став рівним куту CBA.
Порівняйте сторони та кути трикутника ABC з відповідними сторонами та відповідними кутами трикутника A1B1C1 (довжини сторін BC, B1C1, AC, A1C1 і градусні міри кутів BCA і B1C1A1 відображаються на динамічному надписі).
П

одумайте та перевірте, чи не можуть бути рівними кути A1B1C1 і ABC при іншому положенні точки C1 на промені A1D.Яку гіпотезу можна висунути в результаті ваших спостережень П ?
Перевірте вашу гіпотезу для трикутника ABC іншої форми та розмірів.
Порівняйте вашу гіпотезу з теоремою 3.2 підручника.
23. Рівнобедрений трикутник
Трикутник з двома рівними сторонами називається рівнобедреним.
Завдання 23.1
Дослідіть за допомогою ДР “Рівнобедрений трикутник” властивість кутів при основі рівнобедреного трикутника. (На динамічному рисунку вершини B і C трикутника ABC лежать на колі з центром A. Таким чином, AB = AC. Переміщуючи точку P або A, ми можемо змінювати радіус кола, а отже, довжину бічної сторони. Переміщуючи точку B або C по колу ми можемо змінювати довжину основи рівнобедреного трикутника ABC.)
ДР “Рівнобедрений трикутник” можна використати для розв’язування рівнобедреного трикутника, тобто для знаходження за деякими заданими елементами трикутника інших його елементів.
З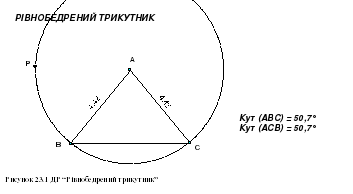
авдання 23.2
Використовуючи ДР “Рівнобедрений трикутник” розв’яжіть задачі:
Дано основу BC і бічну сторону рівнобедреного трикутника ABC. Знайдіть кути трикутника ABC, якщо:
BC = 5, AB = 7;
BC = 7, AB = 5;
BC = 5, AC = 5;
BC = 7, AC = 7.
Дано основу BC і кут при основі рівнобедреного трикутника ABC. Знайдіть два інші кути та бічні сторони трикутника ABC, якщо:
BC = 4, ABC = 45;
BC = 4, ABC = 60;
BC = 6, ACB = 30;
BC = 8, ACB = 30.
Дано основу BC і кут BAC рівнобедреного трикутника ABC. Знайдіть два інші кути та бічні сторони трикутника ABC, якщо:
BC = 8, BAC = 90;
BC = 12, BAC = 90;
BC = 9, BAC = 120;
BC = 9, BAC = 60.
Дано бічну сторону і кут при основі рівнобедреного трикутника ABC. Знайдіть основу та два інші кути трикутника ABC, якщо:
AB = 4, ABC = 45;
AB = 10, ABC = 45;
AC = 6, ABC = 70;
AC = 12, ACB = 70.
Дано бічну сторону і кут при вершині рівнобедреного трикутника ABC. Знайдіть основу та два інші кути трикутника ABC, якщо:
AB = 3,14, BAC = 120;
AB = 8,21, BAC = 90;
AC = 6,28, BAC = 60;
AC = 12,9, BAC = 60.
24. Обернена теорема
Теоремою, оберненою даній, називається така теорема, умовою якої є висновок даної теореми, а висновок — умовою даної теореми. Зазначимо, що обернена теорема до даної правильної теореми може бути як правильною, так і неправильною. Для експериментальної перевірки того, чи правильна обернена теорема, можна використати пакет DG.
Завдання 24.1
В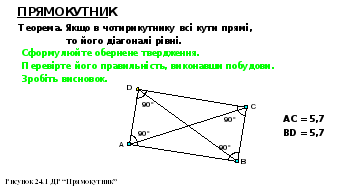
икористовуючи ДР “Прямокутник”, експериментально перевірте таку властивість чотирикутника: Якщо в чотирикутнику всі кути прямі, то його діагоналі рівні. Сформулюйте обернене твердження. Перевірте його правильність, виконавши побудови в пакеті DG.
25. Висота, бісектриса і медіана трикутника
В геометрії трикутника важливу роль відіграють відрізки, які називаються висотами, бісектрисами і медіанами.
Опишемо побудову висоти трикутника ABC, опущеної з вершини C:
Побудуємо пряму, що проходить через вершину C, перпендикулярно до відрізка AB (інструмент Перпендикулярна пряма).
Побудуємо пряму AB (інструмент Пряма).
Знайдемо точку D перетину прямої AB і перпендикуляра, проведеного через вершину C (інструмент Точка перетину). Точка D називається основою висоти тркутника, опущеної із точки C.
П
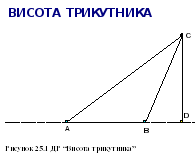 обудуємо відрізок AD (інструмент Відрізок).
обудуємо відрізок AD (інструмент Відрізок).Сховаємо пряму AD. Для цього клацнемо на прямій правою кнопкою миші і виберемо в контекстному меню команду Сховати.
Змінимо стиль прямої AB. В контекстному меню фігури виберемо команду Властивості фігури; в діалоговому вікні, що з’явиться, виберемо Стиль лінії: …….. .
Завдання 25.1
Відкрийте ДР “Висота трикутника”. Скориставшись командою Вид\ Покрокове відтворення побудови, прогляньте виконання побудови.
Дослідіть, при якій умові основа висоти трикутника ABC, проведена із вершини C, належить відрізку AC; збігається з вершиною A; бігається з вершиною B; належить продовженню відрізка AB за точку A; належить продовженню відрізка AB за точку B.
Побудуйте висоти трикутника ABC, опущені з вершин B і C. Яку гіпотезу відносно взаємного розташування прямих, що містять висоти трикутника, можна висунути? Сформулюйте гіпотезу та перевірте її експериментально. П
Побудуйте довільний трикутник ABC. Побудуйте його бісектриси. Яку гіпотезу відносно взаємного розташування бісектрис, можна висунути? Сформулюйте гіпотезу та перевірте її експериментально. П
Побудуйте довільний трикутник ABC. Побудуйте його медіани. П Перевірте експериментально, що медіани трикутника перетинаються в одній точці. Ця точка є центром ваги трикутника. Це означає, що коли трикутник підвісити на нитці, кінець якої закріплено в точці перетину медіан, то він прийме горизонтальне положення. Виріжте із картону довільний трикутник і перевірте, що його центр ваги дійсно збігається з точкою перетину медіан.
Експерименти в математиці відіграють не менш важливу роль, ніж у фізиці. В результаті експериментів у нас виникають правдоподібні гіпотези. Але в фізиці найкращий спосіб переконатися у справедливості висунутої гіпотези полягає у продовженні експериментів. Для доведення своєї гіпотези фізик-експериментатор ставить все нові і більш точні експерименти. В математиці поступають по іншому. Свої твердження математики доводять шляхом логічних міркувань. В результаті виконання завдань, наведених вище, у нас виникли такі гіпотези.
Прямі, що містять висоти трикутника, перетинаються в одній точці.
Медіани трикутника перетинаються в одній точці.
Бісектриси трикутника перетинаються в одній точці.
Ці гіпотези знайшли підтвердження в результаті експериментальної перевірки. Але вони залишаються недоведеними, хоч у нас і виникла глибока впевненість у їх справедливості. Нагадаємо, що при доведенні геометричного твердження ми можемо спиратися на аксіоми і раніше доведені твердження. Використання раніше доведених тверджень спрощує доведення теореми і робить його більш прозорим. Зараз ми знаходимося на початку шляху в Геометричну країну і у нашому розпорядженні небагато доведених теорем. А тому доведення сформульованих вище гіпотез — складна задача. До їх доведення ми повернемося пізніше.
26. Властивість медіани рівнобедреного трикутника
Теорема 3.5 стверджує, що у рівнобедреному трикутнику медіана, проведена до основи, є бісектрисою і висотою. Виникає питання, чи є ця властивість медіани характеристичною для рівнобедреного трикутника, тобто, чи справедливе твердження: якщо медіана трикутника збігається з його висотою або бісектрисою, то трикутник рівнобедрений.
Завдання 26.1
Використовуючи ДР “Висота, медіана і бісектриса трикутника”, дослідіть при якій умові висота CH, медіана CM і бісектриса CK трикутника ABC збігаються.
Доведіть теореми:
Якщо медіана CM і висота CH трикутника ABC збігаються, то трикутник ABC рівнобедрений.
Я
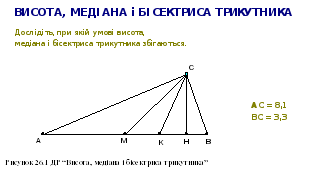
кщо бісектриса CK і висота CH трикутника ABC збігаються, то трикутник ABC рівнобедрений.Якщо медіана CM і бісектриса CK трикутника ABC збігаються, то трикутник ABC рівнобедрений.
27. Третя ознака рівності трикутників
З
авдання 27.1
Дослідіть за допомогою ДР “Третя ознака рівності трикутників”, чи будуть рівними трикутники ABC і A1B1C1, якщо AB = A1B1, AC = A1C1, BC = B1C1. (На динамічному рисунку вершини B1 і C1 трикутника A1B1C1 лежать на колах з центром A1, радіуси яких дорівнюють сторонам AB і AC відповідно. Таким чином, при будь-якому положенні початкових об’єктів AB = A1B1, AC = A1C1.)
Дослідження можна провести за такою схемою:
Задайте параметри трикутника ABC, переміщуючи його вершини (при цьому сторони A1B1 і A1C1 будуть залишатися рівними сторонам AB і AC відповідно).
Переміщуючи точку B1 (або C1), знайдіть таке її положення, щоб відрізки B1C1 і BC стали рівними.
Порівняйте кути трикутника ABC з відповідними кутами трикутника A1B1C1 (градусні міри кутів BCA, CBA, ACB, B1C1A1, C1B1A1 і A1C1B1 відображаються на динамічному надписі).
Перевірте, чи не можуть бути рівними сторони B1C1 і BC при іншому положенні точки C1 на колі (при фіксованому положенні точки B1).
Яку гіпотезу можна висунути в результаті ваших спостережень П ?
Перевірте вашу гіпотезу для трикутника ABC іншої форми та розмірів.
Порівняйте вашу гіпотезу з теоремою 3.6 підручника.
Підказки
Якщо дві сторони і кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними другого трикутника, то такі трикутники рівні.
Якщо сторона і прилеглі до неї кути одного трикутника дорівнюють відповідно стороні й прилеглим до неї кутам другого трикутника, то такі трикутники рівні.
Прямі, що містять висоти трикутника, перетинаються в одній точці.
Бісектриси трикутника перетинаються в одній точці.
Для побудови середин сторін трикутника скористайтеся інструментом Середина відрізка.
Якщо три сторони одного трикутника дорівнюють відповідно трьом сторонам другого трикутника, то такі трикутники рівні.
Просмотр содержимого документа
«05 Geometric construction»
18
38. Коло
Побудови точок, відрізків, променів та прямих
Побудови цих геометричних об’єктів було розглянуто у попередніх параграфах. Їх можна побудувати на практиці за допомогою олівця та лінійки, а в пакеті DG — за допомогою інструментів Точка, Відрізок, Промінь, Пряма відповідно.
Одним із розділів геометрії на площині є геометричні побудови за допомогою циркуля і лінійки. Зауважимо, що циркуль і лінійка в геометрії розглядаються як “математичні”. Так, “математична лінійка” — це інструмент, за допомогою якого можна виконувати деякі визначені дії: сполучати дві точки відрізком; будувати промінь з початком в одній з цих точок і який проходить через другу точку; будувати пряму, яка проходить через ці дві точки. При цьому вважається, що таку “математичну пряму” або “математичний промінь” можна необмежено продовжувати. “Математичний циркуль” — це інструмент, який дозволяє будувати коло за даним радіусом та даним центром. Природа матеріалу, з якого виготовлено “математичну лінійку” або “математичний циркуль”, не мають ніякого значення, як і матеріал, з якого виготовлено папір — об’єкт, на якому власне виконуються геометричні побудови, і спосіб зображення лінії. До речі, папір також вважається “математичним” — необмеженим, абсолютно плоским.
Усі реальні об’єкти, що використовуються для геометричних побудов, є моделями своїх “математичних” прообразів. Пакет DG також дає можливості моделювати геометричні побудови, але тільки моделювати. Більше того, пакет DG можна розглядати як модель геометрії на площині. Ця модель досить досконала — побудови виконуються швидко і точно; розміри області побудов практично необмежені завдяки можливостям масштабування (електронний аналог площини); результати побудови можуть зберігатися і використовуватися для нових побудов; складні побудови можуть виконуватися за один крок, якщо оформити їх у вигляді макросу. Але про все це пізніше.
Зараз для нас важливо навчитися виконувати геометричні побудови засобами пакета DG. І оскільки побудовами за допомогою “електронної лінійки ” ми вже оволоділи, перейдемо до побудов за допомогою “електронного циркуля”.
Побудова Кола
Для побудови кола у пакеті DG є два інструменти:
Коло;
Коло за радіусом.
Побудова кола за допомогою інструмента Коло:
Обрати на панелі геометричних інструмент Коло.
Клацнути мишею в центрі кола.
Клацнути мишею на довільній точці кола.
Обидві точки, що використовувались при побудові кола, є вільними точками і можуть динамічно змінювати своє положення перетягуванням за допомогою миші.
Завдання 38.1
Побудуйте декілька кіл однакового радіуса за допомогою інструмента Коло.
Побудуйте за допомогою інструмента Коло символ олімпіади — п’ять кілець однакового розміру, що розташовані згідно з наведеним рисунком.
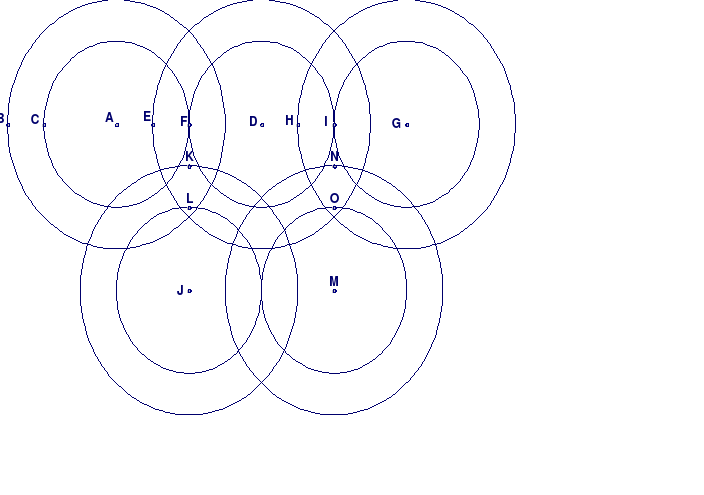
Рисунок 5.1 ДР "Олімпійські кільця"
Зауваження
Послідовність побудови ДР “Олімпійські кільця” можна встановити за іменами точок на рисунку 5.1 — їх алфавітний порядок вказує на послідовність вибору точок.
Для того щоб відповідні кола мали одинакові радіуси, можна скористатися можливістю прив’язки точок до точок координатної сітки — при побудові точок треба держати натиснутою клавішу Shift.
Вибір зручного масштабу можна виконати за допомогою клавіш + або на цифровій клавіатурі.
Побудова кола за допомогою інструмента Коло за радіусом:
Задати радіус кола. Для цього треба клацнути мишею на кінцях відрізка, довжина якого дорівнює радіусу кола (після задання радіуса коло вибраного радіуса “чіпляється” до курсора миші і рухається разом із ним — це зручно для вибору положення кола);
Задати центр кола.
Зауваження
Базовими точками примітива Коло за радіусом є початок та кінець радіуса (за допомогою них можна змінювати радіус кола) і центр кола (за допомогою цієї точки можна змінювати положення кола на площині).
Завдання 38.2
Побудуйте декілька кіл однакового радіуса за допомогою інструмента Коло за радіусом.
Змінюючи положення базових точок, дослідіть, як при цьому буде змінюватися рисунок; порівняйте з ДР, який було побудовано у пункті 1 завдання 38.1.
Побудуйте символ “Олімпійські кільця” за допомогою інструмента Коло за радіусом.
Змінюючи параметри рисунка (положення точок, які задають радіуси та центри кілець), побудуйте різні види символу “Олімпійські кільця”. На рисунку 5.2 зображено варіант розв’язування задачі.

Рисунок 5.2 ДР "Динамічна модель Олімпійських кілець"
Проведіть у класі конкурс на кращий ДР “Олімпійські кільця”, який можна розглядати як моделюючу програму для дизайнерів. Головними критеріями якості програми повинні бути правильність, ефективність, зручність у користуванні.
Придумайте геометричні задачі на тему “Олімпійські кільця”.
Сформулюйте умови, за яких доцільно використовувати інструмент Коло за радіусом, а за яких — інструмент Коло.
Доведіть, що кожну побудову, яку можна здійснити за допомогою інструмента Коло за радіусом, можна виконати за допомогою інструмента Коло і навпаки.
39. Коло, описане навколо трикутника
Дослідження “Центр кола, описаного навколо трикутника”
Побудуйте динамічний рисунок для дослідження властивостей центра кола, описаного навколо трикутника”:
Побудуйте коло, скориставшись інструментом Коло.
Задайте на колі три точки, скориставшись інструментом Точка фігури. Перевірте, чи нові точки дійсно належать колу — при зміні положення вони залишаються на колі.
З’єднайте попарно точки на колі; в результаті буде отримано трикутник, сторони якого є хордами кола.
Опустіть перпендикуляри з центра кола до сторін трикутника.
Знайдіть точки перетину побудованих перпендикулярів зі сторонами трикутника.
Виміряйте довжини відрізків, на які перпендикуляри до сторін трикутника розбивають їх.
Змінюючи положення вершин трикутника на колі, перевірте експериментально, що побудовані перпендикуляри завжди будуть ділити відповідні сторони навпіл1.
Поставте максимальну точність вимірювань в опціях налагодження програми й перевірте експериментально, чи не змінився результат дослідження.
Зробіть висновок відносно положення центра кола, описаного навколо трикутника.
Варіант відповідного ДР “Центр кола, описаного навколо трикутника” наведено на рисунку 5.3.
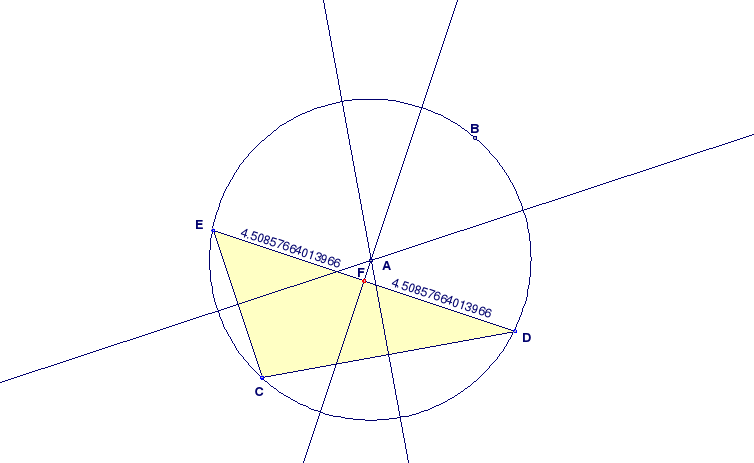
Рисунок 5. 3 ДР "Центр кола, описаного навколо трикутника"
Природно задати питання, чи потрібне доведення експериментально перевіреного факту, тобто, чи можна вважати доведеною відповідну теорему?
З наукової точки зору
Необхідність дедуктивних доведень
Кожна теорема стверджує, що деякий факт має місце завжди, коли виконується умова теореми (наприклад, для довільного трикутника ... або для довільних натуральних чисел ....), а експерименти, які підтверджують справедливість теореми, стосуються тільки окремих випадків. За допомогою відповідної комп’ютерної програми, наприклад DG, можна підтвердити справедливість теореми для великої кількості окремих випадків, але все ж таки тільки для скінченої множини окремих випадків.
Таким чином, ніякі експериментальні підтвердження теореми не усувають необхідності її точного дедуктивного доведення. І це не є недоліками якогось конкретного комп’ютерного пакета, наприклад, пакета DG, а є принциповою необхідністю дедуктивних доведень (доведень за допомогою законів логіки).
Необхідність комп’ютерних експериментів
Якщо все в математиці вимагає дедуктивного доведення, то навіщо проводити експерименти, зокрема комп’ютерні експерименти, наприклад, експерименти у середовищі пакета DG?
Кожна теорема, її твердження може виникнути тільки на основі дослідження властивостей конкретних об’єктів, які дані досліднику в експерименті, неважливо, в якому саме експерименті: натурному, комп’ютерному або уявному. Теореми не написано на якихось Мойсейових скрижалях, теореми є результатом винаходу дослідника. Винахід цей можна зробити тільки на основі експериментування — розгляду окремих випадків.
Якщо теорема неправильна, то може пощастити у процесі експерименту знайти контрприклад до теореми (тобто окремий випадок, для якого твердження теореми не виконується) і тим самим спростувати твердження. Звичайним є випадок, коли після побудови контрприкладу теорему уточнюють — обмежують область визначеності теореми так, щоб відповідну властивість мали всі об’єкти.
Якщо теорема правильна, то її підтвердження в конкретних випадках за допомогою експериментів може допомогти у знаходженні доведення теореми — за допомогою пакета можна досліджувати властивості довільних характеристик і вони можуть щось підказати. Крім того, у дослідника формується внутрішня психологічна впевненість у справедливості теореми, залишається тільки необхідність знайти доведення.
Тому, спробуйте довести справедливість теореми про центр кола, описаного навколо трикутника самостійно, а якщо виникнуть труднощі, скористайтеся допомогою (підручника, комп’ютера, товаришів, батьків або вчителя).
40. Дотична до кола
Згідно з означенням, дотична до кола — це пряма, що проходить через точку кола перпендикулярно до радіуса кола, проведеного у цю точку. Зрозуміло, дотичну до кола легко побудувати засобами пакета DG. Побудова складається з двох кроків: побудувати радіус кола і побудувати перпендикуляр до цього радіуса. Сконструюємо макрос, який дозволяє виконувати ці побудови за один крок — викликати макрос TangentToCircle (який ми зараз сконструюємо) і вказати точку на колі, через яку проходить дотична. Зрозуміло, комп’ютер буде виконувати ті ж два кроки, проте виконувати їх він буде автоматично.
Розробка макросу TangentToCircle:
Побудуйте довільне коло, скориставшись інструментом Коло.
Поставте на колі довільну точку, скориставшись інструментом Точка фігури.
Проведіть радіус в побудовану точку кола, скориставшись інструментом Відрізок.
Побудуйте дотичну до кола, скориставшись інструментом Перпендикулярна пряма.
Оберіть команду Макроси\Створити макрос.
Задайте вихідні об’єкти макросу — центр кола та точку на колі.
Оберіть команду Макроси\Завершити вибір вихідних об’єктів.
Задайте результуючий об’єкт — дотичну до кола.
Оберіть команду Макроси\Завершити вибір результуючих об’єктів.
Збережіть макрос: скориставшись вікном діалогу, задайте папку для зберігання макросу і задайте його ім’я — TangentToCircle.
Протестуйте правильність роботи макросу:
Побудуйте довільне коло.
Побудуйте довільну точку на колі.
Оберіть макрос — команда Макроси\TangentToCircle.
Вкажіть за допомогою миші центр кола і точку на колі — пакет DG повинен автоматично побудувати дотичну.
Проведіть комп’ютерні експерименти, змінюючи положення точки на колі, центра та радіуса кола — дотична повинна автоматично змінювати своє положення. При цьому доцільно вивести на екран величину кута між дотичною та радіусом за допомогою інструмента Виміряти кут.
Проведіть експерименти, змінюючи масштаб (клавіші + і - на цифровій клавіатурі). Якщо дотична зникає з екрана при збільшенні масштабу, перемістіть за допомогою миші рисунок так, щоб точка дотику була близькою до центра екрана.
41. Коло, вписане у трикутник
Дослідження “Центр кола, вписаного у трикутник”
Розробіть динамічний рисунок для дослідження властивостей центра кола, вписаного в трикутник:
Побудуйте коло, скориставшись інструментом Коло.
Задайте на колі три точки, скориставшись інструментом Точка фігури. Перевірте, що нові точки дійсно належать колу — при зміні положення вони залишаються на колі.
Проведіть радіуси кола у побудовані точки, скориставшись інструментом Відрізок, сполучивши центр кола з побудованими точками.
Побудуйте перпендикуляри до побудованих радіусів у точках кола. Побудовані прямі будуть дотичними до кола у даних точках. Динамічно змінюючи положення точок на колі перевірте експериментально, що побудовані прямі дійсно будуть дотичними до кола.
Знайдіть точки перетину побудованих прямих, скориставшись інструментом Точка перетину. Точки перетину будуть утворювати вершини трикутника, описаного навколо заданого кола.
З’єднайте центр кола з вершинами трикутника, скориставшись інструментом Відрізок.
Виміряйте величини кутів,. Скористайтеся для цього інструментом Виміряти кут.
Перевірте експериментально, що величини кутів, які утворюють радіуси зі сторонами трикутника рівні (принаймні з великою точністю).
Проаналізуйте ваші спостереження і сформулюйте гіпотезу про центр кола, вписаного в трикутник.
Спробуйте довести сформульовану вами гіпотезу. У разі виникнення труднощів скористайтеся підручником або допомогою друзів.
Проведіть експерименти з побудованим динамічним рисунком з метою відкриття нових геометричних фактів.

Рисунок 5.4 ДР "Властивості кола, вписаного у трикутник"
42. Що таке задачі на побудову
З наукової точки зору
За суттю задачі на побудову полягають не стільки в тому, щоб отримати фігуру, яка відповідає умовам задачі, а в тому, щоб знайти загальне правило побудови результуючої фігури за вихідними даними. Таке правило у вік інформатики правильно називати алгоритмом. Знайомство з теорією алгоритмів складає основу шкільного курсу інформатики. Циркуль та лінійка за термінологією інформатики є інструментами для виконання команд, які може здійснювати виконавець алгоритмів. Для геометрії це завжди була людина, яка виконувала побудови. При цьому важлива чітка формалізація команд, які може здійснювати виконавець. Для геометрії цими командами є команди побудови прямої, що проходить через дві задані точки, побудови кола за заданим центром та заданим радіусом і знаходження точки перетину двох побудованих ліній (двох прямих, прямої і кола, двох кіл). Тільки для цих цілей можуть використовуватися циркуль і лінійка. Для виконання цих операцій використовуються уявні (“математичні”) циркуль та лінійка, за допомогою яких можна проводити нескінченно довгі прямі, кола довільного радіуса, побудовані за їх допомогою лінії є нескінченно тонкими (“завтовшки в одну точку”). Моделями таких інструментів на практиці завжди служили фізичні лінійки, циркулі, які тією чи іншою мірою задовольняли потреби практики, але, зрозуміло, ніколи не збігалися з їх математичними прототипами. У пакеті DG також реалізовані моделі “математичного циркуля” та “математичної лінійки”, і за багатьма властивостями вони перевершують властивості інших моделей, зокрема моделей фізичних. Проте завжди треба мати на увазі, що можливостями пакета DG як інструмента геометричних побудов є сукупність команд, які моделюють “математичні” інструменти побудов — циркуль та лінійку. І тому, якщо не вказано протилежне, цими інструментами можна виконувати тільки команди, які можуть виконувати “математичні” циркуль та лінійка.
43. Побудова трикутника з даними сторонами
Задача 5.1.
Побудувати трикутник з даними сторонами a, b, c.
Дослідження “Побудова трикутника з даними сторонами”
Розробіть динамічний рисунок “Побудова трикутника з даними сторонами”:
Побудуйте довільний промінь, скориставшись інструментом Промінь. Одна із сторін трикутника буде лежать на промені і одна із його вершин буде збігатися з початком променя.
Задайте три довільні відрізки, скориставшись інструментом Відрізок. Довжини цих відрізків будуть задавати довжини сторін трикутника.
Відкладіть одну із сторін трикутника на промені від його початку (для цього скористайтеся інструментом Коло за радіусом — побудуйте коло радіусом, рівним вибраній стороні трикутника і з центром у початку променя, і знайдіть точку перетину побудованого кола з променем). Кінці цього відрізка будуть двома вершинами шуканого трикутника.
Побудуйте коло радіусом, рівним другій стороні трикутника і з центром, що збігається з початком променя.
Побудуйте коло радіусом, рівним третій стороні трикутника і з центром у кінці відрізка, відкладеного на промені.
Знайдіть точку перетину двох побудованих кіл — це буде третя вершина шуканого трикутника.
Сполучіть вершини трикутника відрізками.
Перевірте експериментально, чи побудований трикутник — шуканий (довжини його сторін збігаються з довжинами заданих відрізків). Для цього скористайтесь інструментом Виміряти відстань.
Доведіть, що побудований трикутник — шуканий (відповідає умовам задачі).
Проведіть експерименти з побудованим динамічним рисунком з метою дослідження умов, за яких трикутник за заданими трьома сторонами існує. Сформулюйте гіпотезу про умови, яким повинні відповідати довжини трьох відрізків, щоб існував трикутник зі сторонами, рівними цим відрізкам.
Доведіть або спростуйте гіпотезу: трикутник, сторони якого рівні трьом заданим відрізкам, існує тоді і тільки тоді, коли сума довжин будь-яких двох із цих відрізків перевищує довжину третього відрізка.
44. Побудова кута, що дорівнює даному
Побудова макросу “Кут за п’ятьма точками”
Розглянемо задачу 5.2. під кутом зору створення макросу — послідовності дій у пакеті DG, яку можна викликати за іменем і яка виконується автоматично після задання вихідних параметрів макросу. Нагадаємо постановку задачі 5.2.
Задача 5.2
Відкласти від даної півпрямої в дану півплощину кут, що дорівнює даному куту.
Оскільки таку задачу в геометричних побудовах доводиться розв’язувати досить часто, доцільно створити макрос і кожен раз, коли виникає потреба, використовувати його.
Перед створенням будь-якого макросу необхідно спочатку проаналізувати:
алгоритм побудови, який буде виконуватися макросом (зрозуміло, спочатку такі алгоритми треба сконструювати);
повноту та незалежність вихідних параметрів макросу (інакше задача буде або невизначеною, або некоректною; пакет видасть про це відповідне повідомлення);
які об’єкти будуть результуючими;
зручність використання макросу, зокрема дати йому ім’я (найкраще ім’я — мнемонічне, тобто таке ім’я, з якого зрозуміло призначення макросу)2.
У нашому випадку відповіді на ці запитання будуть такими:
алгоритм буде спиратися на запропонований у підручнику спосіб побудови трикутника, рівного даному (див. задачу 5.1).
За вихідні дані приймемо три точки, що визначають кут (точка на стороні, вершина кута, точка на другій стороні, причому сторони вказуються проти годинникової стрілки), та дві точки, що визначають промінь (на якому буде лежать сторона шуканого кута).
Результуючим об’єктом буде кут — два промені, які утворюють кут, що дорівнює вихідному куту.
Дамо макросу ім’я AngleBy5Points.
Можна розглядати й інші способи задання вихідного та результуючого кута (наприклад, вихідний і результуючий кути можна задавати відповідними відрізками), але нам здається, що обраний спосіб задання кутів є найзручнішим.
Завдання 44.1
Сконструюйте макрос AngleBy5Points побудови кута, рівного даному:
Створіть новий рисунок, використовуючи команду Новий у розділі меню Файл.
Задайте вихідні точки макросу — 5 точок.
Аналогічно алгоритму побудови трикутника, рівного даному, побудуйте результуючий кут.
Сховайте всі допоміжні побудови, використовуючи команду Сховати у відповідних контекстних меню об’єктів.
Перейдіть у режим створення макросу — команда Макроси\Створити макрос.
Укажіть вихідні об’єкти клацанням на них мишею (запам’ятайте послідовність задання вихідних об’єктів; тільки в такій послідовності треба буде задавати їх при використанні макросу — інакше використання макросу буде некоректним).
Перейдіть у режим задання результуючих об’єктів — команда Макроси\Завершити вибір вихідних об’єктів.
Задайте результуючі об’єкти: у нашому випадку — два промені, які визначають кут.
Оберіть команду Макроси\Завершити вибір резльтуючих об’єктів.
Укажіть місце зберігання макросу за допомогою стандартного вікна діалогу і задайте ім’я AngleBy5Points.
Впевніться, що макрос AngleBy5Points з’явився в розділі меню Макроси. Тепер для його використання достатньо обрати команду Макроси\ AngleBy5Points і, слідкуючи за підказками пакета в рядку статусу, вказати вихідні об’єкти для побудови кута, рівного даному — відповідний кут буде побудовано автоматично.
Протестуйте макрос, для чого побудуйте декілька кутів, рівних даному, виміряйте їх величини, динамічно змінюючи вихідні параметри, впевніться, що відповідно будуть змінюватися й результуючі кути.
Як приклад використання розробленого макросу AngleBy5Points розглянемо в наступному пункті задачу поділу кута на три рівні частини — одну з трьох найвідоміших стародавніх задач геометрії.
45. Побудова бісектриси кута
Ми не будемо розглядати побудову бісектриси кута за допомогою циркуля та лінійки й реалізацію цього алгоритму в межах пакета DG.
Ніяких труднощів на цьому шляху немає, крім того, оскільки ця побудова досить часто використовується на практиці, до складу стандартних інструментів пакета DG включено інструмент Бісектриса. Замість цього розглянемо цікаву стародавню задачу про поділ кута на три рівні частини — задачу про трисекцію кута. Ця задача має для нас інтерес з багатьох точок зору — про це йдеться далі, а зараз це приклад доцільного використання макросів.
Задача “Трисекція кута”
Поділити кут на три рівні частини.
Розробіть динамічний рисунок “Трисекція кута”.
Задайте кут — шаблон (за допомогою зміни величини цього кута-шаблона будемо ділити на три рівні частини довільний кут). Для цього побудуйте два промені, які виходять зі спільної точки.
Побудуйте довільний кут — даний кут, який треба поділити на три рівні частини.
Відкладіть на стороні даного кута кут-шаблон за допомогою макросу AngleBy5Points.
На стороні відкладеного кута-шаблона (що не збігається зі стороною даного кута) відкладіть повторно кут-шаблон за допомогою макросу AngleBy5Points.
Повторіть ще раз попередній крок алгоритму, відклавши втретє кут- шаблон на стороні кута, побудованого на попередньому кроці.
У результаті на стороні даного кута побудовано кут, втричі більший від кута–шаблона. Змінюючи положення точок, які визначають кут-шаблон, можна знайти таке їх положення, при якому візуально сторона даного кута та побудованого третього кута-шаблону будуть збігатися. У цьому положенні сторони кута-шаблона, що розташовані всередині шуканого кута, будуть ділити його на три рівні частини. Відповідний ДР AngleTrisection розташоване в папці \Student Guide\05 Geometric Construction\05 Geometric Construction (DGF). Копію екрана наведено на рисунку 5.6.
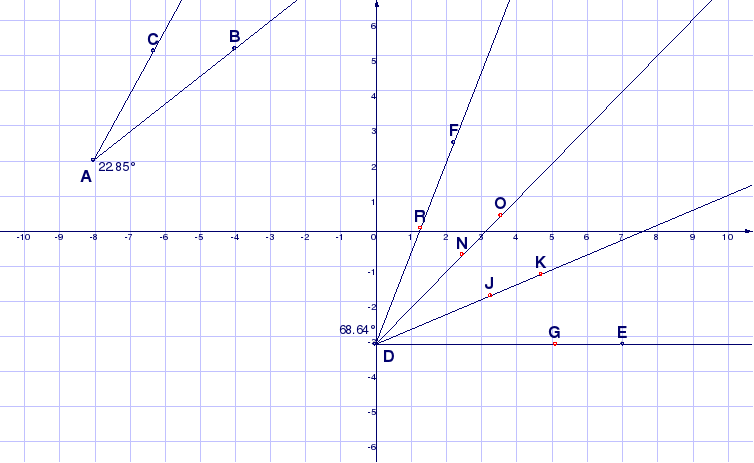
Рисунок 5.6 ДР “Трисекція кута”
З наукової точки зору
Задачу трисекції кута безуспішно розв’язували математики протягом більше двох тисячоліть. Однак у 1837 році німецький математик П.Ванцель довів, що розв’язати її за допомогою циркуля та лінійки неможливо.
Чи дозволяє ДР AngleTrisection розв’язувати задачу точно?
Зрозуміло, ні — ДР AngleTrisection дозволяє тільки наближено розв’язувати цю задачу. Проте, якщо використовувати масштабування, задачу трисекції кута можна розв’язувати за допомогою ДР AngleTrisection із досить великою точністю, до 10 десяткових знаків і навіть більше. Спробуйте зробити це самостійно.
Якщо вас зацікавила задача трисекції кута, ви можете створити більш досконалі інструменти засобами пакета DG. Ви також можете познайомитись із видатними стародавніми проблемами геометрії за літературою, посилання на яку можна знайти, наприклад, у математичній енциклопедії або в Інтернет, набравши у пошуковій системі фразу “трисекція кута” або “angle trisection”.
Ви можете також самостійно попрацювати над проектом “Ділення кута на n рівних частин”, причому розглянути розв’язування задачі за допомогою циркуля та лінійки, за допомогою інших інструментів, точні розв’язання та наближені розв’язування тощо.
46. Ділення відрізка навпіл
Для розв’язування цієї задачі в пакеті DG також є стандартний інструмент — Середина відрізка. Ми пропонуємо самостійно створити макрос ділення відрізка навпіл і протестувати його. Крім цього, пропонуємо поміркувати над задачею поділу відрізка на n рівних частин. На відміну від задачі про поділ кутів на n рівних частин цю задачу можна розв’язати за допомогою циркуля та лінійки. Один (однак не єдиний) шлях до розв’язування цієї задачі дає теорема Фалеса, яка вивчається у наступному параграфі.
47. Побудова перпендикулярної прямої
Для розв’язування цієї задачі в пакеті DG також є стандартний інструмент — Перпендикулярна пряма. Ми пропонуємо самостійно створити макрос побудови перпендикулярної прямої і протестувати його. При побудові використовуйте базові точки прямої. Створити макрос, який працює подібно інструменту пакета (тобто, щоб вихідними об’єктами була пряма і точка), вам не вдасться — для цього треба використовувати аналітичну геометрію і “завітати” до самої програми пакета DG.
48. Геометричне місце точок
У пакеті DG є три можливості для побудови геометричних місць точок:
Побудова слідів (траєкторій точок) при динамічних змінах рисунків.
Побудова динамічних слідів (динамічних траєкторій точок) — при зміні параметрів рисунка динамічно змінюються і траєкторії точок, які перед тим були побудовані (команда Фігури\Побудови\Динамічний слід).
Побудова ліній, які задані аналітичними рівняннями.
Для демонстрації цих можливостей розглянемо задачу про падаючу драбину.
Задача про падаючу драбину
Драбина приставлена до вертикальної стіни. На середній сходинці драбини стоїть відерце з фарбою. Драбина сповзає вниз так, що її верхній кінець рухається по стіні, а нижній — по підлозі. Знайти траєкторію відерця з фарбою при русі драбини.
Зрозуміло, що абстрактною моделлю задачі буде рух відрізка постійної довжини так, що його кінці лежать на двох взаємно перпендикулярних прямих. Знайти траєкторію руху середньої точки відрізка.
Побудуйте динамічний рисунок “Падаюча драбина”:
Побудуйте горизонтальну пряму — “підлогу”, по якій буде ковзати драбина, скориставшись інструментом Пряма і використовуючи прив’язку до вузлів координатної сітки (натисніть клавішу Shift при побудові базових точок прямої).
Аналогічно побудуйте вертикальну пряму — “стіну”.
Побудуйте відрізок, довжина якого буде відповідати довжині драбини.
Побудуйте точку на вертикальній прямій — точку дотику драбини і стіни.
Побудуйте коло радіусом, що дорівнює довжині драбини, з центром у точці дотику драбини до стіни.
Знайдіть точку перетину побудованого кола з горизонтальною прямою — точку дотику драбини з підлогою.
Побудуйте драбину — відрізок, який сполучає побудовані точки на горизонтальній та вертикальній прямих.
Побудуйте середину драбини, скориставшись інструментом Середина відрізка.
Виберіть команду Залишати слід для середньої точки драбини. Для цього скористайтеся контекстним меню точки — Властивості сліду\Залишати слід.
Побудуйте траєкторію відерця з фарбою. Для цього динамічно змінюйте положення базової точки драбини — точку дотику драбини зі стіною.
Дослідження траєкторії відерця з фарбою
Вигляд траєкторії нагадує чверть кола з центром у точці, що належить лінії перетину підлоги і стіни, тому достатньо побудувати відповідне коло, щоб експериментально в цьому переконатися. Таким чином приходимо до гіпотези: Відерце з фарбою рухається по колу, радіус якого дорівнює половині довжини драбини.
Спробуйте самостійно довести це твердження.
1 Оскільки обчислення в комп’ютері проводяться наближено, можливі розходження довжин у старших розрядах.
2 Не можна утриматися від прикладів влучних мнемонічних імен: НСД — найбільший спільний дільник, ICQ — I seek you, MS — MicroSoft і т.п.
Просмотр содержимого документа
«06 Quadrilaterals»
12
50. Означення чотирикутника
Перед систематичним вивченням властивостей чотирикутника, доцільно створити динамічний рисунок “Чотирикутник” і провести експерименти з ним.
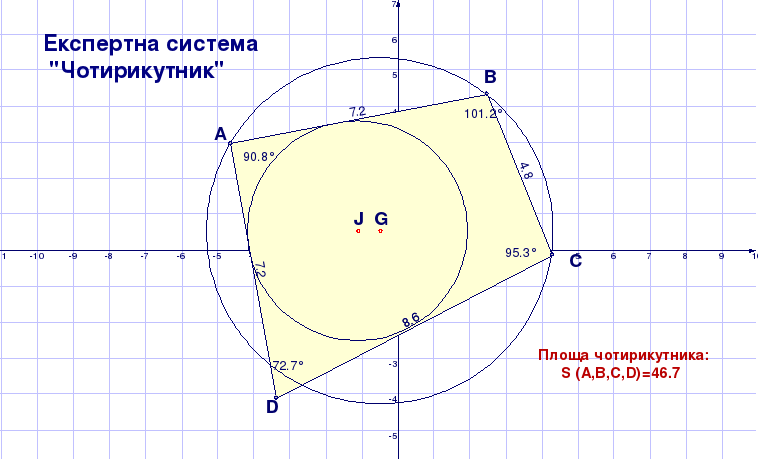
Рисунок 6.1 ДР “Експертна система “Чотирикутник””
Варіант такого ДР наведено на рисунку 6.1.
При побудові динамічного рисунка “Чотирикутник” був використаний інструмент Многокутник.
Чотирикутник ABCD – довільний (його вершини можна переміщувати по площині). На ДР виводяться довжини сторін та величини кутів чотирикутника. Крім того, побудовано два кола:
коло, яке проходить через три вершини чотирикутника: A, B та C,
коло, яке є дотичним до трьох сторін чотирикутника: AB, DC, AD.
Побудувати ці кола можна безпосередньо або скористатися відповідними макросами, які було розроблено у попередньому параграфі:
CircleThrough3Points — побудова кола, яке проходить через три задані точки;
InscribedCircle — побудова кола, вписаного в трикутник1.
Побудовані кола можна використати, наприклад, для дослідження умов, за яких навколо чотирикутника можна описати коло або вписати в нього коло. (Ці питання досліджуються докладно далі, але вже зараз можна спробувати експериментально знайти вище задані умови).
Завдання 50.1
Побудуйте ДР “Експертна система “Чотирикутники”” згідно з
рисунком 6.1.Доповніть ДР “Експертна система “Чотирикутники” додатковими можливостями досліджень:
Побудуйте діагоналі та виміряйте їх довжини;
Виведіть у надпис величину периметра многокутника та суми довжин його протилежних сторін, скориставшись командою Редагування\Добавити надпис2 ;
Виведіть у надпис суми протилежних кутів чотирикутника аналогічно попередньому пункту.
Проведіть експерименти з метою виявлення умов, за яких навколо чотирикутника можна описати коло або у чотирикутник можна вписати коло.
Доповніть ДР “Експертна система “Чотирикутники”” власними додатковими можливостями досліджень.
Проведіть експерименти із вдосконаленим вами ДР “Експертна система “Чотирикутники”” з метою виявлення загальних властивостей чотирикутників.
Навчально – дослідницький проект
Дослідіть кількість точок, в яких можуть перетинатися бісектриси кутів довільного чотирикутника.
51. Паралелограм
Завдання 51.1
Для дослідження властивостей паралелограма побудуйте ДР “Експертна система “Паралелограм”” згідно з рисунком 6.2.
Запустіть пакет DG або виберіть команду Файл\Новий у меню вже завантаженого пакета.
Збережіть ДР у відповідній папці (наприклад, ...\Geometry\8A\Sidorenko Sasha) з ім’ям ExpertSystem (Paralelogram).
Побудуйте три довільні точки A, B, C, які будуть базовими (вільними) точками — вершинами паралелограма.
Побудуйте сторони AB, BC.
Побудуйте залежну вершину D . Для цього:
Побудуйте пряму, паралельну стороні AB, що проходить через точку C;
Побудуйте пряму, паралельну стороні BC, що проходить через точку A;
Знайдіть точку перетину побудованих прямих — четверту вершину D паралелограма.
Побудуйте шуканий паралелограм, скориставшись командою Фігури\Побудови\Многокутник. Після цього налагодьте його зовнішній вигляд, скориставшись послугами контекстного меню.
Виміряйте величини довжин сторін паралелограма та його кути.
Доповніть ДР “Експертна система “Паралелограм”” власними додатковими можливостями досліджень;
Проведіть експерименти з ДР “Експертна система “Паралелограм” з метою виявлення загальних властивостей паралелограмів.
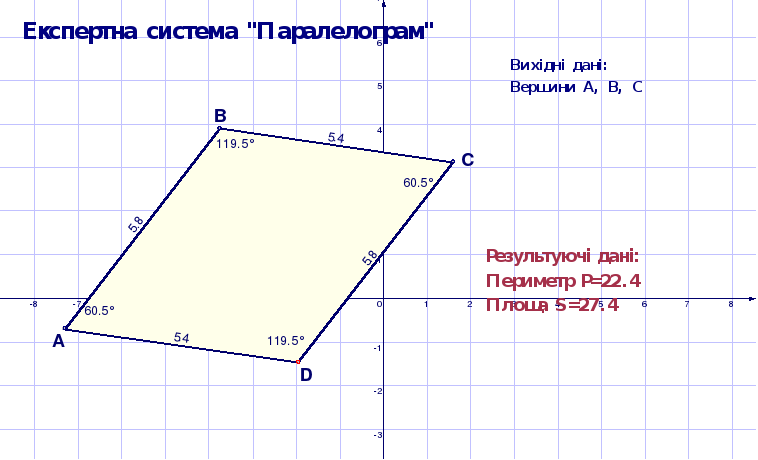
Рисунок 6.2 ДР "Експертна система "Паралелограм"”
Завдання 51.2
Побудуйте ДР “Властивості діагоналей паралелограма” згідно з
рисунком 6.3 з метою дослідження умов на діагоналі чотирикутника, за яких він є паралелограмом:
Побудуйте довільний чотирикутник, скориставшись командою Фігури\Побудови\Многокутник. Після цього налагодьте його зовнішній вигляд, скориставшись послугами контекстного меню.
Побудуйте діагоналі паралелограма.
Знайдіть точку перетину діагоналей паралелограма.
Виміряйте довжини відрізків, на які розбиваються діагоналі чотирикутника точкою їх перетину.
Через сторони чотирикутника проведіть прямі (для того щоб зручніше було визначати, коли чотирикутник перетворюється у паралелограм).
Проведіть дослідження умов на діагоналі чотирикутника, за яких він перетворюється у паралелограм.
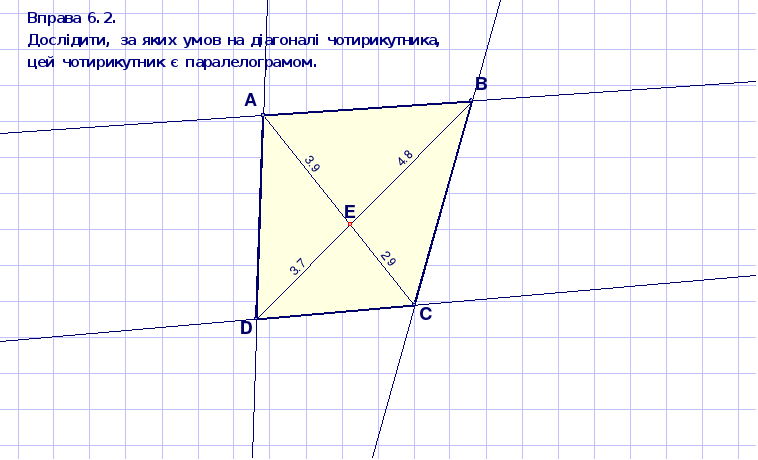
Рисунок 6.3 ДР “Властивості діагоналей паралелограма”
52. Властивість діагоналей паралелограма
Розроблений у попередньому пункті ДР “Експертна система “Паралелограм” може бути також використаний для дослідження властивостей діагоналей паралелограма. Для цього необхідно побудувати на ДР діагоналі паралелограма, знайти їх точку перетину і виміряти довжини відрізків, на які діляться
діагоналі точкою перетину. Такі експерименти дозволяють на практиці впевнитися, у справедливості теореми 6.2.
Задачу 6.6 природно сформулювати у формі дослідження.
Завдання 52.1
Через точку перетину діагоналей паралелограма проведено пряму. Дослідити її властивості.
Для розв’язування задачі можна виконати комп’ютерні експерименти за допомогою ДР “Експертна система “Паралелограм”” або спеціально побудувати відповідний ДР. Експериментально знайдені закономірності треба довести дедуктивно. Як неодноразово наголошувалося, за допомогою ДР можна тільки сформувати гіпотезу, після чого її треба довести або спростувати. Для спростування гіпотези достатньо побудувати контрприклад до неї, тобто знайти конкретну ситуацію, в якій гіпотеза неправильна. Для цього можна і треба ефективно використовувати комп’ютерні моделі взагалі і DG зокрема. Для доведення гіпотез пакет DG і комп’ютерні експерименти можна використовувати тільки як допоміжний засіб для знаходження допоміжних, проміжних гіпотез. Нагадаємо, що доведення математичного факту (теореми) складається з послідовності допоміжних, проміжних “маленьких” теорем, сукупність яких і утворює дедуктивне доведення.
53. Властивості протилежних сторін і кутів паралелограма
Розроблений у попередньому пункті ДР “Експертна система “Паралелограм”” можна використати для дослідження властивостей протилежних сторін і кутів паралелограма.
Задачу 6.18 також природно cформулювати у дослідницькій формі.
Завдання 53.1
Дослідіть властивості чотирикутника, якщо відомо, що дві його протилежні сторони рівні й паралельні.
Для дослідження задачі побудуйте динамічний рисунок. Не забувайте, що правильний ДР повинен давати можливість отримувати довільний рисунок, що відповідає умовам задачі за допомогою базових точок. Нижче наведено один із можливих варіантів побудови ДР “Задача 6.18”
Побудова ДР “Задача 6.18”
Побудуйте відрізок AB і точку C , що не лежить на прямій AB.
Побудуйте пряму, що проходить через точку С паралельно відрізку
AB.Поставте за допомогою інструмента Точка фігури на побудованій прямій точку D.
Відкладіть на побудованій прямій відрізок CD, рівний відрізку AB, скориставшись інструментом Коло за радіусом.
Побудуйте чотирикутник ABCD.
За допомогою експериментів впевніться, що чотирикутник ABCD — паралелограм. Це можна зробити різними способами, наприклад, так:
побудувати пряму BC;
провести через точку B пряму, паралельну відрізку AD;
максимально зменшуючи масштаб ДР (клавіша на цифровій клавіатурі), впевніться, що побудовані прямі збігаються3.
На рисунку 6.4 наведено ДР “Задача 6.18” на етапі проведення комп’ютерних експериментів.
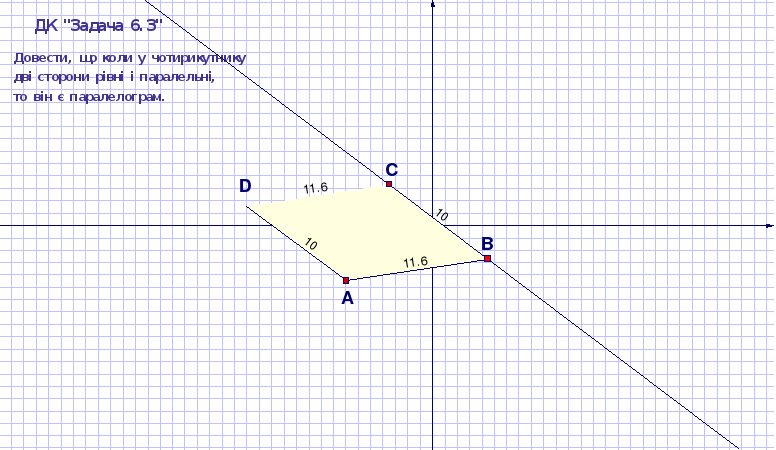
Рисунок 6.4 ДР “Задача 6.18”
На рисунку 6.5 наведено вікно діалогу “Властивості фігури”, з якого можна отримати рівняння лінії –— у нашому випадку прямої, паралельної прямій AD, що проходить через точку B.
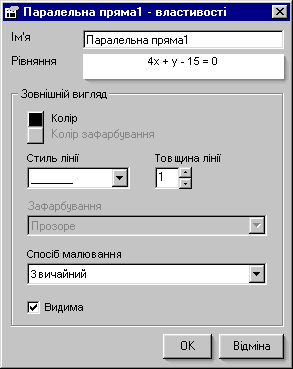
Рис. 6.5 Діалогове вікно «Властивості фігури»
54. Прямокутник
Побудуємо ДР “Експертна система “Прямокутник”” для дослідження властивостей прямокутника, наближеного розв’язування задач, спираючись безпосередньо на означення прямокутника.
Побудова ДР “Експертна система “Прямокутник”
Побудуйте сторону AB прямокутника, скориставшись інструментом Відрізок.
Побудуйте перпендикулярну пряму до відрізка AB у точці A, скориставшись інструментом Перпендикулярна пряма.
Побудуйте третю вершину D прямокутника. Вершина D — напівзалежна (вона лежить на прямій, що перпендикулярна до сторони AB). Для її побудови скористайтеся інструментом Точка фігури. Якщо точці буде автоматично присвоєне інше ім’я, наприклад C, то точку треба перейменувати, скориставшись вікном діалогу Властивості точки, яке можна викликати з контекстного меню цієї точки. Його наведено на рисунку 6.6.
Побудуйте перпендикулярну пряму до сторони AD , що проходить через точці D, скориставшись інструментом Перпендикулярна пряма.
Побудуйте перпендикулярну пряму до сторони AB у точці B, скориставшись інструментом Перпендикулярна пряма.
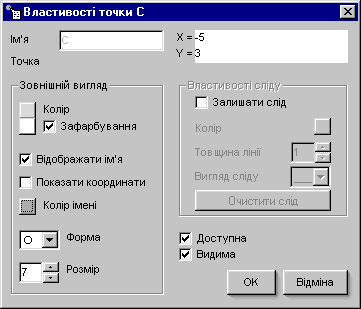
Рис. 6.6 Діалогове вікно «Властивості точки»
Знайдіть точку перетину двох перпендикулярів, що були побудовані у двох попередніх пунктах, скориставшись інструментом Точка перетину — це буде четверта вершина C прямокутника.
Виміряйте величини сторін і кутів побудованого прямокутника.
За допомогою переміщення базових точок прямокутника (точки A, B, D) переконайтесь, що побудований чотирикутник є дійсно прямокутником, до того ж ДР побудовано коректно — модель завжди є моделлю прямокутника і модель довільного прямокутника можна побудувати за допомогою ДР.
Побудуйте діагоналі прямокутника.
Виміряйте довжини діагоналей.
Створіть надписи згідно з рисунком 6.7. Для динамічних обчислень площі та периметра прямокутника в надпис необхідно додати відповідні формули для обчислення периметра та площі (рис. 6.8).
Використовуючи розроблений ДР “Експертна система “Прямокутник””, можна досліджувати властивості прямокутників, зокрема рівність його діагоналей. За допомогою експериментів неважко переконатися, що справедлива, теорема: паралелограм є прямокутником тоді і тільки тоді, коли його діагоналі рівні. Як часто буває, доведення цього факту не складніше за саме його “відкриття”. ДР — це зручний інструмент для “відкриття” математичних закономірностей.
Слово “відкриття” ми беремо у лапки, оскільки вони є такими тільки учня. Проте DG за своїми можливостями моделювати геометричні об’єкти та маніпулювати ними дозволяють робити справжні математичні відкриття, і в матеріалах пакету є приклади нових геометричних результатів, відкриттю яких сприяли експерименти з відповідними ДР у середовищі DG.
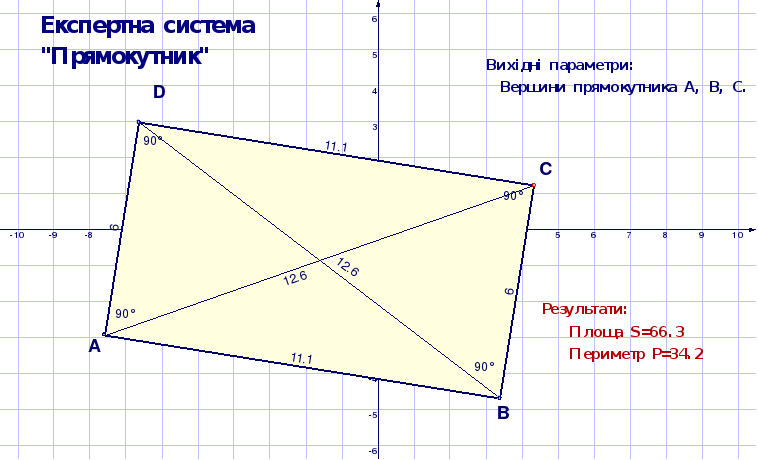
Рисунок 6.7 ДР "Експертна система "Прямокутник"
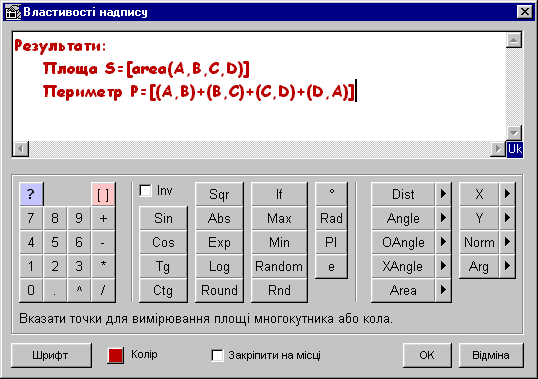
Рисунок 6.8 Створення надписів
Завдання 54.1
Наведіть якомога більше прикладів використання на практиці прямокутників. Спробуйте знайти обґрунтування цього факту.
55. Ромб
Побудуємо ДР “Експертна система “Ромб””, виходячи з означення ромба. Розроблений ДР будемо далі використовувати для дослідження властивостей ромба — проведення експериментів для формування гіпотез, їх експериментального підтвердження та наближеного розв’язування задач.
Побудова ДР “Експертна система “Ромб””
Побудуйте довільний відрізок AB — сторону ромба, скориставшись інструментом Відрізок.
Побудуйте коло з центром у точці A і радіусом AB, скориставшись інструментом Коло.
Побудуйте точку D на колі, скориставшись інструментом Точка фігури (при необхідності перейменуйте точку).
Побудуйте відрізок AD, скориставшись інструментом Відрізок.
Через точку B проведіть пряму, паралельну відрізку AD, скориставшись інструментом Паралельна пряма.
Через точку D проведіть пряму, паралельну відрізку AB, скориставшись інструментом Паралельна пряма.
Знайдіть точку перетину побудованих прямих, скориставшись інструментом Точка перетину — четверту вершину ромба C.
Виміряйте довжини сторін і величини кутів ромба, скориставшись інструментами Виміряти довжину і Виміряти кут.
Побудуйте діагоналі ромба, скориставшись інструментом Відрізок.
Виміряйте довжини діагоналей ромба скориставшись інструментом Виміряти довжину.
Виміряйте площу ромба, скориставшись інструментом Виміряти площу.
Проведіть експерименти з розробленим ДР для перевірки його коректності: при довільному положенню базових точок A, B, D будується ромб; довільний ромб можна отримати при відповідному положенні базових точок.
Виміряйте кути між діагоналями ромба, скориставшись інструментом Виміряти кут.
Дослідіть властивості ромба, змінюючи форму ромба.
Зображення динамічного рисунка представлено на рисунку 6.9.
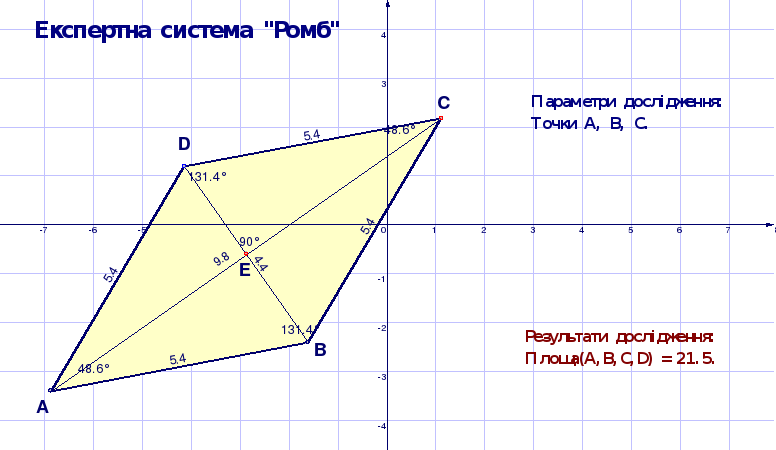
Рисунок 6.9 ДР "Експертна система "Ромб"
1 Треба побудувати коло, яке вписане у трикутник, утворений стороною AD та продовженнями відрізків AB та CD.
2 Нагадаємо, що динамічний вираз можна вставити у надпис у квадратних дужках, використовуючи функції, які підтримує пакет DG, наприклад, вивести величину периметра чотирикутника можна за допомогою виразу “Периметр P = [DIST(A,B)+ DIST (B,C)+ DIST (C,D)+ DIST (D,A)]”.
3 Замість візуальної перевірки співпадання двох прямих, можна було б впевнитися, що ці прямі мають однакові рівняння (рівняння прямої вивчається пізніше, у параграфі 8). Для цього з контекстних меню цих прямих треба обрати команди Властивості фігури і порівняти наведені в них рівняння прямих.
Просмотр содержимого документа
«07 Pythagorean Theorem»
20
62. Косинус кута
Для того щоб експериментально впевнитися, що теорема 7.1 про залежність косинуса тільки від градусної міри кута і незалежність від положення й розмірів прямокутного трикутника є справедливою, можна скористатися пакетом DG. Варіант відповідного ДР наведено на рисунку7.1. На перший погляд, може скластися враження, що наведений ДР дещо ускладнений. Ви можете побудувати свій варіант ДР — це було б корисним для вас, а потім результат порівняти з ДР, представленим у бібліотеці. Ще раз наголосимо: для якісного проведення комп’ютерного експерименту щодо перевірки деякої гіпотези геометрична фігура (ДР) з одного боку, не повинна мати ніяких додаткових властивостей, крім визначених у гіпотезі, а з іншого — мати всі властивості, які задано умовами гіпотези. Такі вимоги задовольняє ДР "Косинус гострого кута прямокутного трикутника". Трикутник ABC задовольняє всі умови теореми: його положення можна змінювати, рухаючи базові точки: точка P визначає величину кута, точка A — положення вершини трикутника, точка B — напрям та доажину катета. У результаті експериментів ми можемо впевнитися, що при фіксованій величині кута косинус з точністю до чотирьох знаків не залежить від положення та величини прямокутного трикутника. Треба окремо обговорити точність проведення обчислень. При точності більше 5 знаків вже помітна похибка обчислень як результат наближеності обчислення значень функцій та виконання арифметичних операцій. Але ми й не намагалися довести теорему, ми спробували тільки впевнитися на прикладах у справедливості теореми. Доведення теореми наведено в підручнику.
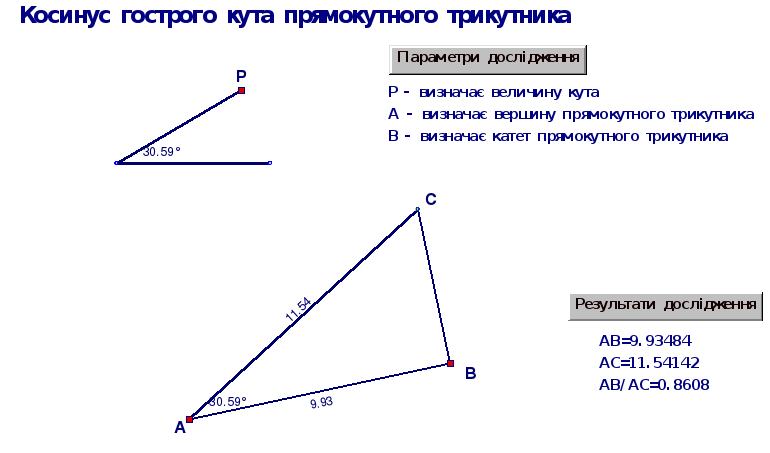
Рисунок 7.1 ДК "Косинус гострого кута прямокутного трикутника"
63. Теорема Піфагора
За допомогою ДК можна експериментально знаходити співвідношення між його елементами. Для цього треба використовувати результати вимірювань довжин відрізків, величин кутів, площ многокутників, які можна знайти за допомогою відповідних інструментів:
Виміряти відстань
Виміряти кут
Виміряти площу.
Якщо співвідношення складне, то краще зробити динамічний надпис, в якому можна розмістити і пояснювальний текст, і власне динамічний надпис, в якому результати обчислень будуть автоматично перераховуватися при переміщенні базових точок ДР.
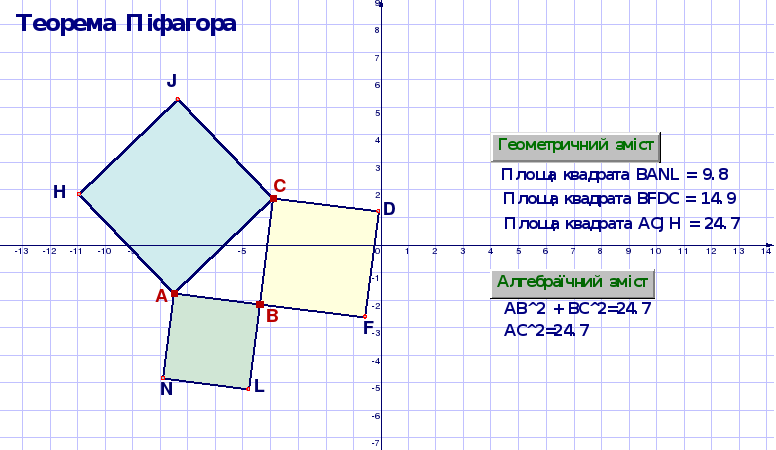
Рисунок 7.2 ДР “Теорема Піфагора”
Розглянемо розробку ДР “Теорема Піфагора”.
Спочатку розробимо макрос SquareBy2Points для побудови квадрата за двома суміжними вершинами. Це варто зробити, оскільки нам прийдеться будувати квадрат тричі: на гіпотенузі прямокутного трикутника та на його катетах, крім того цей макрос нам ще не раз буде у нагоді при різних побудовах.
Розробка макросу SquareBy2Points:
Розпочніть побудову нового рисунка, скориставшись кнопкою на стандартній панелі інструментів Створити новий рисунок.
Побудуйте дві довільні точки — вершини квадрата, які є вихідними даними для майбутнього макросу, скориставшись командою Точка.
Побудуйте відрізок, який сполучає побудовані точки — сторону майбутнього квадрата, скориставшись інструментом Відрізок.
Побудуйте перпендикуляри до побудованого відрізка в його кінцях, скориставшись інструментом Перпендикулярна пряма.
Відкладіть на одному з перпендикулярів відрізок, який дорівнює стороні квадрата:
Побудуйте коло, скориставшись інструментом Коло з центром в одному кінці відрізка й радіусом, який дорівнює стороні квадрата.
Знайдіть точку перетину побудованого кола з перпендикуляром до побудованого відрізка, скориставшись інструментом Точка перетину.
Побудуйте відрізок, який з’єднує знайдену точку з центром кола, скориставшись інструментом Відрізок.
Побудуйте перпендикуляр до побудованого відрізка в його кінці, скориставшись інструментом Перпендикулярна пряма.
Знайдіть точку перетину побудованого перпендикуляра з побудованим раніше — останню четверту вершину квадрата, скориставшись інструментом Точка перетину.
Побудуйте дві останні сторони квадрата, скориставшись інструментом Відрізок.
Сховайте всі допоміжні побудови, скориставшись контекстним меню об’єктів і обираючи в ньому команду Сховати.
Запишіть макрос:
Виберіть команду Макроси\Створити макрос.
Задайте вихідні об’єкти макросу — дві точки.
Виберіть команду Макроси\Завершити вибір вихідних об’єк-тів.
Задайте результуючі об’єкти — сторони квадрата.
Виберіть команду Макроси\Завершити вибір результуючих об’єктів.
Задайте у вікні діалогу ім’я макросу SquareBy2Points.
Виберіть папку для зберігання макросу і збережіть його.
Впевніться, що макрос працює правильно — для цього побудуйте декілька квадратів, наприклад, розгортку куба (рис. 7.3).
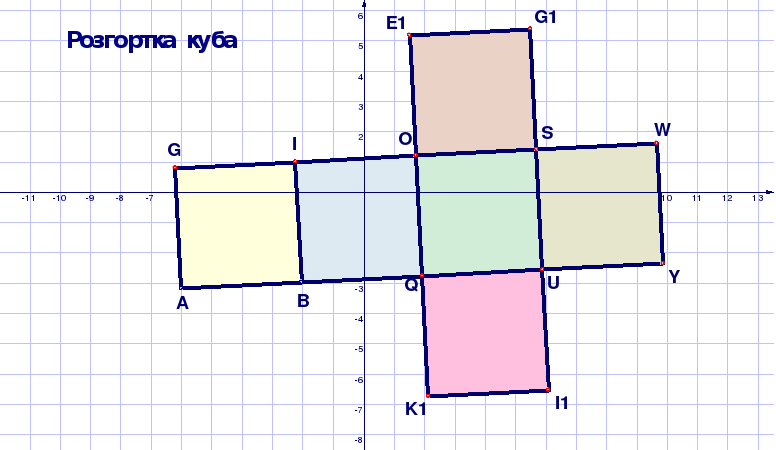
Рисунок 7.3 ДР “Розгортка куба”
Розробка ДР “Теорема Піфагора”
Побудуйте прямокутний трикутник:
Побудуйте довільний відрізок (катет майбутнього прямокутного трикутника), скориставшись інструментом Відрізок;
Побудуйте перпендикуляр до побудованого відрізка, який проходить через його кінець, скориставшись інструментом Перпендикулярна пряма;
Побудуйте на перпендикулярі довільну точку (третю вершину прямокутного трикутника), скориставшись інструментом Відрізок;
Побудуйте відрізки які сполучають побудовану вершину з кінцями вихідного відрізка (гіпотенузу та другий катет), скориставшись інструментом Відрізок;
Сховайте допоміжні побудови (команда Сховати контекстного меню об’єкта).
Побудуйте квадрати на сторонах побудованого прямокутного трикутника:
Завантажте макрос SquareBy2Points, скориставшись командою Макроси \ Завантажити макрос;
Побудуйте квадрати на сторонах прямокутного трикутника:
Активізуйте макрос SquareBy2Points, обираючи однойменну команду з розділу меню Макроси;
Задайте вихідні об’єкти макросу, клацаючи мишею на двох вершинах трикутника, згідно з підказкою у контекстному меню1.
Виміряйте величини площ квадратів, скориставшись командою Виміряти площу.
Відредагуйте надписи, скориставшись командами контекстного меню надписів.
Впорядкуйте розроблений ДР відповідно своїм вподобанням.
Впевніться, що розроблений ДР працює коректно (можна змоделювати довільний прямокутний трикутник, площі квадратів обчислюються правильно); для цього протестуйте ДР на прикладах, параметри яких вам відомі.
Після того, як ви впевнитесь, що розроблений ДР працює правильно, проведіть з ним комп’ютерні експерименти з метою знаходження закономірностей змін параметрів геометричної конфігурації.
Після певної кількості експериментів можна помітити, що сума квадратів катетів дорівнює квадрату гіпотенузи. Але поки що це тільки гіпотеза, яка виконується на деякій множині конкретних прикладів. Щоб збільшити кількість досліджених випадків, не проводячи обчислення вручну (знаходження суми квадратів катетів), зробимо динамічний надпис, в якому ця сума буде обчислюватись автоматично.
Розробка динамічного надпису (загальні питання)
Спочатку обговоримо питання розробки динамічного надпису взагалі, а потім розробимо конкретний надпис для обчислення суми квадратів катетів.
Розробка надпису виконується за допомогою вікна діалогу Властивості надпису. Текст надпису можна вводити безпосередньо з клавіатури, редагуючи параметри шрифту та колір за допомогою стандартних вікон діалогу Windows, які викликаються за допомогою кнопок Шрифт та Колір відповідно. Довільний фрагмент тексту, включений у квадратні дужки, розглядається пакетом як динамічний вираз — тобто математична формула, значення якої буде динамічно обчислюватися у відповідності зі зміною параметрів ДР. Динамічний вираз повинен бути побудований за правилами алгебри з використанням констант, змінних та функцій, назви яких наведено на панелі вводу у вікні діалогу Властивості надпису (див. рисунок 7.4).
Не занурюючись глибоко у деталі підготовки динамічних виразів, зробимо лише декілька зауважень, а деталі будемо обговорювати далі у контексті задач, які будуть розглядатися.
Рожева кнопка призначена для введення квадратних дужок, якими обрамляється вираз.
Перемикач Inv призначений для вибору прямих або обернених тригонометричних функцій (наприклад, sin або arcsin). Якщо ви з ними ще не знайомі — не біда, скоро познайомитесь.
Символ градусів виконує дві функції — це просто символ у звичайному тексті і це ознака обчислення величини кутів у градусах (за умовчанням кути вимірюються в радіанах).
Параметри геометричних об’єктів можна вимірювати за допомогою відповідних функцій2:
Об’єкт Точка:
Абсциса — кнопка X або вираз Ім’я точки.X, наприклад, A.X ;
Ордината — кнопка Y або вираз Ім’я точки.Y, наприклад, A.Y;
Полярний радіус точки (відстань точки від початку координат) — кнопка Norm або вираз Norm(Ім’я точки), наприклад, Norm(P);
Полярний кут точки (величина кута між додатним напрямком осі абсцис та променем, проведеним у задану точку з початку координат — кнопка Arg або вираз Arg(), наприклад, Arg(P) або Arg(P) у залежності від того, в якому вигляді треба подавати результати вимірювання кута — у радіанах або градусах.
Об’єкт Відрізок:
Довжина відрізка – кнопка Distance або вираз Dist(, ), або вираз (, ), або вираз , , наприклад, Dist(A,B) або (A,B) або AB;
Об’єкт Кут:
Величина кута (кут задається трьома точками: перша — на стороні кута, друга — вершина кута, третя — на іншій стороні кута) — кнопка Angle або вираз Anаgle(, , ), наприклад, Angle(A,B,C) або Angle(A,B,C) у залежності від того, в якому вигляді треба подавати результати вимірювання кута — у радіанах чи градусах;
Величина орієнтованого кута (орієнтованість означає, що вимірюваний кут дорівнює куту, на який треба повернути першу сторона кута проти годинникової стрілки до збігання з другою стороною кута) — кнопка OAngle або вираз OAngle(, , ), наприклад, OAngle(A,B,C) або OAngle(A,B,C) у залежності від того, в якому вигляді треба подавати результати вимірювання кута — у радіанах чи градусах;
Об’єкт Многокутник або Коло:
Площа многокутника — кнопка Area або вираз Area(, ,...,N,), наприклад, Area(A,B,C,D) площа чотирикутника ABCD;
Площа кола — кнопка Area або вираз Area(Ім’я центра кола, Ім’я точки на колі), наприклад, Area(A,B) площа кола з центром у точці A та точкою на колі B.
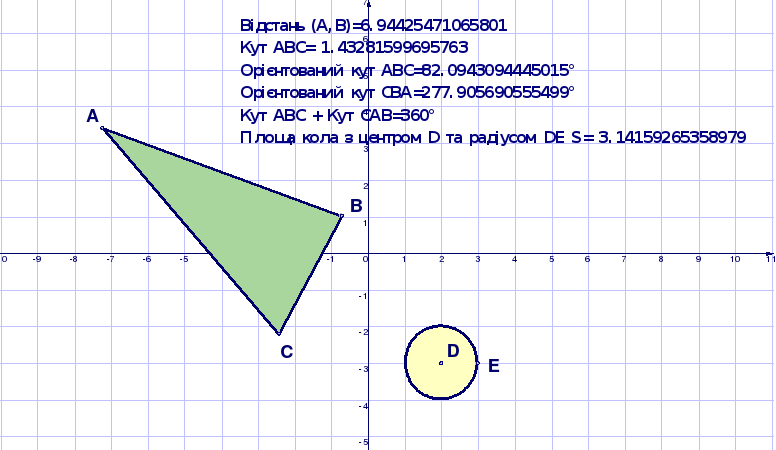
Рисунок 7.4 ДР “Використання динамічних виразів у надписах”
Нами обговорено інструментарій і загальні питання конструювання динамічних виразів і їх використання у надписах, тепер можна приступити до створення динамічних виразів для ДР Теорема Піфагора.
Розробка динамічного надпису для ДР “Теорема Піфагора”
Визвати вікно діалогу “Вставити надпис” і внести в нього текст згідно з рисунком 7.5.
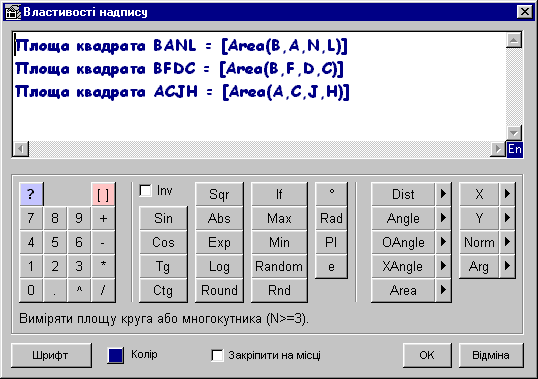
Рисунок 7.5 Вікно діалогу “Властивості надпису”
Звернемо увагу на те, що динамічні вирази треба заключати у квадратні дужки, а також, що синтаксис динамічних виразів повинен бути витриманий у строгій відповідності з домовленостями. Наприклад, якщо замість виразу [Area (B, A, N, L)] ввести вираз [Площа (B, A, N, L)] або [Aria (B, A, N, L)], то пакет видасть повідомлення про помилку (див. рисунок 7.6), яка буде відображатися поки всі синтаксичні помилки не будуть виправлені.
А
налогічно треба ввести інші надписи, використовуючи вікно діалогу “Властивості надпису”.
Тепер можна провести експерименти з підготовленим ДР “Теорема Піфагора” і впевнитися, що теорема справедлива для будь-яких прямокутних трикутників.
При цьому, як завжди, виникає два питання:
Як до цього результату можна дійти самостійно або, як до цього дійшов Піфагор?
Чи доводять наші експерименти теорему Піфагора?
Відповідь на перше питання складна і невтішна: невідомо, як самостійно доходити до відкриття та доведення теорем. Можна скористатися відомим прийомом, який є фольклорним для математиків і який описаний у відомій книзі “Фізики жартують”: “Для того щоб розв’язати рівняння його треба написати, а потім дивитися на нього до тих пір, поки розв’язування не прийде в голову.”. Якщо без жартів, то і формулювання теорем, і їх доведення є прикладами алгоритмічно невирішуваних задач, тобто немає загальних правил, слідуючи яким можна відкрити теорему або її довести. До того ж не можна відтворити хід думки Піфагора, коли він відкривав або доводив цю теорему. Доцільно також згадати, що існує багато інших доведень, кожне з яких несе печатку ходу думки свого автора. Є геометричні доведення, які можна добре ілюструвати за допомогою пакета DG. І останнє: за впливовістю на математику в цілому теорема Піфагора рекордсмен, і на могилі Піфагора, за його заповітом, зображені “Піфагорові штани” — рисунок, який ми виконали у пакеті DG. Це говорить про те, що Піфагор сам відчував красу і важливість цієї теореми.
Відповідь на питання, чи довели ми в результаті комп’ютерних експериментів теорему Піфагора, зрозуміло, негативна — доведення у математиці може бути тільки дедуктивним. Це єдина принципова відмінність математики від інших наук, як природничих, так і гуманітарних. У підручнику наведено варіант доведення, який спирається на теорему Фалеса.
64. Єгипетський трикутник
Теорема Піфагора стверджує, що для прямокутного трикутника виконується співвідношення: квадрат гіпотенузи дорівнює сумі квадратів катетів. А якщо у деякому трикутнику квадрат однієї зі сторін дорівнює сумі квадратів двох інших, чи можна стверджувати, що найбільша зі сторін лежить навпроти прямого кута? Розв’язування задачі 7.17 показує, що можна. Це дає ключ до побудови прямих кутів за допомогою замкненої мотузки, вузли якої ділять її у відношення 3:4:5. Трикутник, сторони якого задовольняють наведену умову, називається єгипетським. Якщо відповідним чином підібрати одиницю довжини, то довжини сторін єгипетського трикутника виражаються цілими числами. А чи існують інші прямокутні трикутники, довжини сторін яких виражаються цілими числами (крім, зрозуміло, тих, сторони яких кратні сторонам єгипетського трикутника, наприклад, 6 метрів, 8 метрів та 10 метрів)? Кого зацікавить ця задача, може познайомитися з літературою з теорії діофантових рівнянь (так звуться рівняння, розв’язки яких шукається у цілих числах). Рівняння ![]() , де x, y і z — цілі числа, є прикладом діофантового рівняння. Ви можете самостійно пошукати інші цілочисельні розв’язки цього рівняння. За допомогою DG можна сконструювати спеціалізований ДР для пошуку єгипетських трикутників.
, де x, y і z — цілі числа, є прикладом діофантового рівняння. Ви можете самостійно пошукати інші цілочисельні розв’язки цього рівняння. За допомогою DG можна сконструювати спеціалізований ДР для пошуку єгипетських трикутників.
Розробка ДР “Пошук єгипетських трикутників”
Відобразіть осі координат — команда Вид\Осі координат. Зауважимо, що осі координат є геометричними об’єктами: їх можна використовувати у геометричних побудовах.
Побудуйте прямокутний трикутник згідно з рисунком 7.7.
Поставте точки A та B на координатних осях.
Побудуйте відрізок AB.
Знайдіть точку перетину координатних осей — точку C.
Побудуйте трикутник ABC, скориставшись інструментом Многокутник.
Підготовте динамічний надпис, в якому розмістіть довжини катетів та гіпотенузи трикутника ABC.
За допомогою комп’ютерних експериментів знайдіть інші єгипетські трикутники. Нагадаємо: щоб рухомі точки прив’язувалися до сітки, треба виконувати переміщення точки при натиснутій клавіші Shift. Для того, щоб було більше впевненості у знаходженні єгипетських трикутників треба встановити достатньо велику точність, наприклад, 10 знаків, скориставшись для цього установками у розділі головного меню Опції \ Опції \ Різне \Точність чисел.
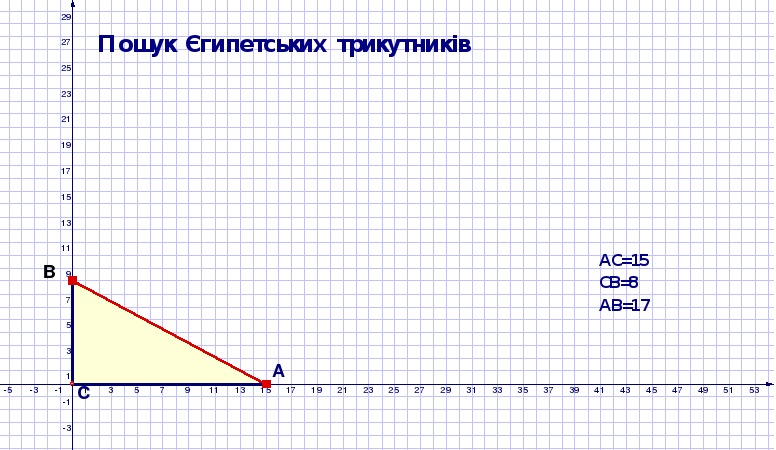 Рисунок 7.7 ДР “Пошук єгипетських трикутників”
Рисунок 7.7 ДР “Пошук єгипетських трикутників”
На рисунку наведено один із знайдених єгипетських трикутників. Впевніться за допомогою обчислювань, що знайдений трикутник дійсно є єгипетським.
Завдання 7.68.1
Знайдіть якомога більше єгипетських трикутників за допомогою розробленого ДР. Перевірте обчисленнями, що знайдені трикутники дійсно є єгипетськими трикутниками.
69. Значення синуса, косинуса й тангенса деяких кутів
Засобами пакета DG не складає труднощів побудувати ДР, який дозволяє обчислювати значення тригонометричних функцій для будь-яких кутів. Варіант такого ДР обговорюється у наступному параграфі, але було б за краще, спробувати такий ДР самостійно.
Завдання 7.69.1
Розробити ДР “Обчислення значень тригонометричних функцій.”
70. Зміна синуса, косинуса й тангенса при зростанні кута
Сконструюємо ДР “Обчислення значень тригонометричних функцій”
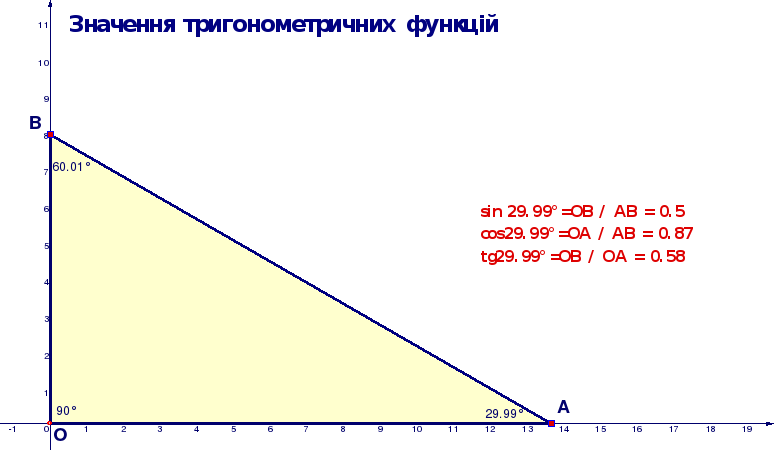
Рисунок 7.8 ДР “Обчислення значень тригонометричних функцій”
Побудувати точки A та B на координатних осях (нагадаємо, що координатні прямі побудовані за допомогою примітивів Пряма і тому можуть використовуватися при побудовах).
Побудувати точку перетину координатних осей — точку O, скориставшись інструментом Точка перетину.
Побудувати трикутник OAB, скориставшись примітивом Многокутник.
Виміряти кути трикутника OAB, скориставшись інструментом Виміряти кут.
Підготувати динамічний надпис згідно з рисунком 7.9.
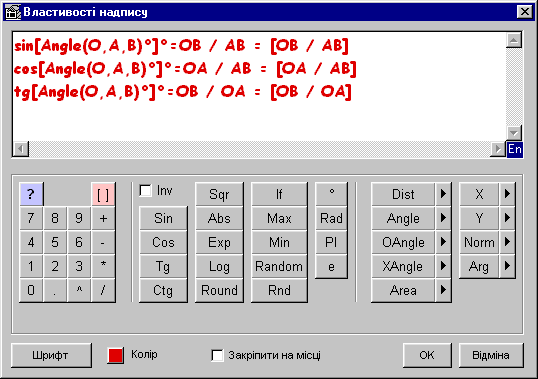
Рисунок 7.9 Динамічний надпис до ДР "Значення тригонометричних функцій"
Підготовлений ДР можна використовувати для дослідження значень та властивостей тригонометричних функцій, а також для наближеного обчислення значень функцій. Для цього достатньо побудувати трикутник з відповідним кутом за допомогою переміщення точок A та B. Як завжди, виникають проблеми з точністю. Вручну можна забезпечити побудову кутів з довільною кількістю точних знаків у інтервалі [ 1 .. 10] , для цього треба відповідним чином змінити масштаб рисунка (клавіші “+” та “-“ на числовій клавіатурі). Чим більше розміри трикутника, тим точніше вручну можна встановити величину кута. Відповідна точність обчислювань значень функцій буде принаймні 6 знаків. Таким чином, підготовлені нами динамічні рисунки поглинають можливості багатьох математичних довідників, наприклад, довідника “Чотиризначні математичні таблиці” за редакцією В.М. Брадіса. Втім, зрозуміло, зручніше використовувати для наближених значень функцій звичайний інженерний калькулятор.
Зауваження
Точні значення функцій за допомогою розробленого ДР не можна знайти, значення ж тригонометричних функцій для кутів 0, 30, 45, 60, 90 можна вивести тільки дедуктивним методом.
Чи можна за допомогою пакета DG довести тотожність?
Доведення тотожностей — творча справа. Доведено, що взагалі не існує правил (алгоритмів) для доведення тотожностей — це алгоритмічно невирішувана задача. Системи, які можна використовувати для напівавтоматичного доведення теорем, називаються пакетами комп’ютерної алгебри — CAS (Computer Algebra System). Ці пакети можуть тотожньо перетворювати алгебраїчні вирази за вказівками користувача. Для DG ця задача навіть не може обговорюватися серйозно, оскільки обчислення виконуються у DG наближено. Проте, комп’ютерні експерименти можуть підтвердити вірогідність справедливості тотожності, або допомогти побудувати контрприклад до гіпотези. Щоб продемонструвати ці можливості можна взяти вираз — “кандидата на тотожність” і побудувати для нього ДР, в якому змінні “кандидата” будуть задаватися параметрами рухомих точок.
Наприклад. візьмемо вираз ![]() . Перетворимо його тотожньо:
. Перетворимо його тотожньо:
![]() і ліву частину цього виразу введемо в динамічний вираз ДР “Обчислення значень тригонометричних функцій”, замість значень функцій введемо відношення, які їх визначають. На рисунку 7.10 зображено ДР “Експериментальна перевірка тотожностей”, у якому встановлено точність чисел, яка дорівнює 10 знакам після десяткової коми. На основі експериментів ми бачимо, що значення виразу завжди незмінне — дорівнює нулю (треба пам’ятати, що це означає тільки виконання тотожності з точністю принаймні 6 знаків і тільки для тих значень кутів, які ми зможемо встановити за допомогою DG. Тим самим, ми перевірили, що вірогідність справедливості тотожності досить висока. Звичайно, не зважаючи на це, тотожність потребує дедуктивного доведення.
і ліву частину цього виразу введемо в динамічний вираз ДР “Обчислення значень тригонометричних функцій”, замість значень функцій введемо відношення, які їх визначають. На рисунку 7.10 зображено ДР “Експериментальна перевірка тотожностей”, у якому встановлено точність чисел, яка дорівнює 10 знакам після десяткової коми. На основі експериментів ми бачимо, що значення виразу завжди незмінне — дорівнює нулю (треба пам’ятати, що це означає тільки виконання тотожності з точністю принаймні 6 знаків і тільки для тих значень кутів, які ми зможемо встановити за допомогою DG. Тим самим, ми перевірили, що вірогідність справедливості тотожності досить висока. Звичайно, не зважаючи на це, тотожність потребує дедуктивного доведення.
Розглянемо інший приклад: чи є тотожністю вираз: ![]() ?
?
Знову виконаємо тотожні перетворення, переносячи праву частину рівності у ліву з протилежним знаком, і сконструюємо ДР “Експериментальна перевірка тотожностей з двома змінними” (дивись рисунок 7.11).
Дві точки A та B обрані на осі абсцис. Відповідні вирази для динамічного виразу наведено на рисунку 7.12.
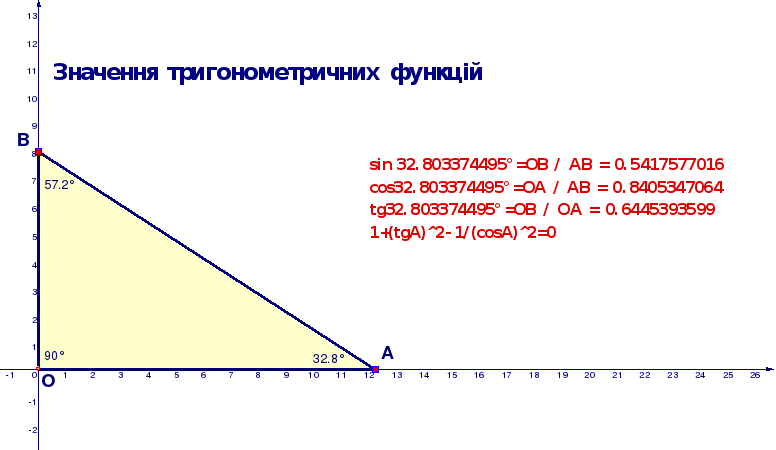
Рисунок 7.10 ДР “Експериментальна перевірка тотожностей”
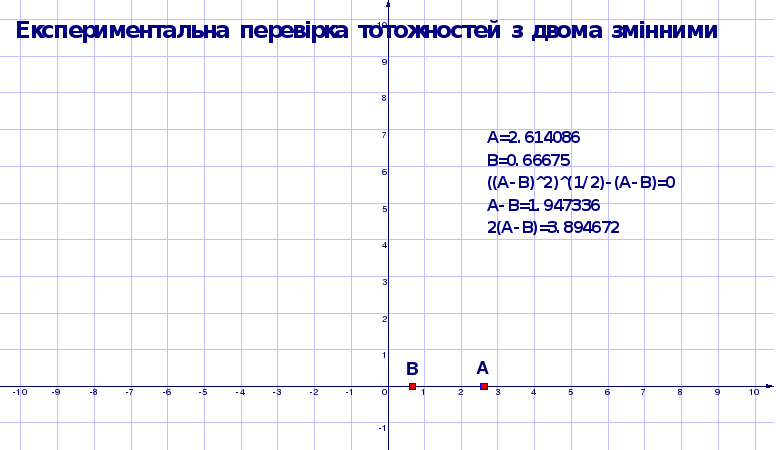
Рисунок 7.11 ДР “Експериментальна перевірка тотожностей з двома змінними”
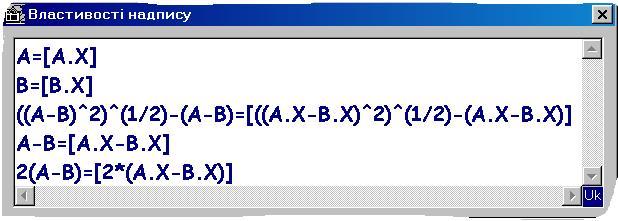
Рисунок 7.12 Динамічний виразу до ДК "Експериментальна перевірка тотожностей з двома змінними"
На коментар потребують тільки змінні A.X та B.X — це абсциси точок A та B відповідно, їх ординати зберігаються у змінних A.Y та B.Y.
Зміст динамічного виразу відбиває можливий шлях пошуку тотожностей. Спочатку було введено перші три вирази. Потім експерименти показали, що третій вираз не є тотожність. Проте сформувалася гіпотеза, що величина виразу пов’язана з різницею A – B. Після чергових експериментів з’явилася гіпотеза, що величина третього виразу дорівнює подвійній різниці A – B у випадку, коли A B. І останній рядок є вираз для перевірки цієї гіпотези. Експерименти з цим виразом підтвердили експериментально гіпотезу. Дедуктивне доведення справедливості тотожності
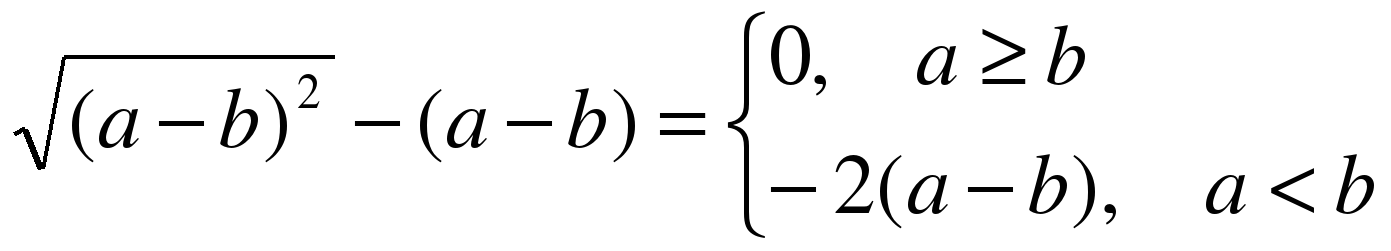
нескладне — достатньо розглянути кожний з випадків окремо.
У такий спосіб можна досліджувати на тотожність вирази з будь-яким числом змінних.
ДР можна використовувати як інструмент дослідження у багатьох випадках, зокрема, практично на кожну задачу підручника можна подивитись як на тему дослідження — можливо узагальнити умови задачі або навпаки їх більше конкретизувати, пошукати аналогії в інших галузях, подумати над її застосуванням на практиці і т.п. Як приклад, розглянемо задачу 7.31.
Задача 7.31.
На прямолінійному шосе треба знайти місце для автобусної зупинки так, щоб сума відстаней від неї до населених пунктів A і B була найменшою. Розгляньте два випадки:
Населені пункти розміщені з різних боків від шосе;
Населені пункти розміщені з одного боку від шосе.
Варіант ДР для цієї задачі наведено на рисунку 7.13 (нагадаємо, що ми вже обговорювали деякі можливості використання цього динамічного рисунка раніше).
Зрозуміло, наведений ДР є “вороновою” інтерпретацією для другої частини задачі. За допомогою ДР можна знайти шукану точку з довільною точністю (якщо змінювати масштаб ДР). Після знаходження шуканої точки можна знайти умову, якій ця точка повинна задовольняти — це рівність кутів посадки та зльоту ворони. Задачу можна узагальнити, якщо згадати, що швидкість зльоту та посадки різні. У цьому випадку за допомогою циркуля та лінійки задачу розв’язати не завжди можливо, але наближено ми її можемо розв’язати з довільною точністю. Для цього треба модифікувати відповідним чином динамічний рисунок — ввести замість функції, яка визначає величину L, замість виразу [IJ + JH], наприклад, вираз [IJ + 2*JH], якщо швидкість посадки вдвічі більше швидкості зльоту.
Ця узагальнена задача має багато прикладних переформулювань — як знайти місце для зупинки на трасі, що мінімізує сумарну відстань, яку проходять мешканці населених пунктів A і B. Самостійно придумайте інтерпретації для випадків, коли замість дороги розглядається газопровід або канал і треба подати газ або воду у кількості, яка пропорційна кількості мешканців населених пунктів A і B. Всі ці задачі можна розв’язувати наближено (з точністю до 13 знаків!) за допомогою ДР "Задача про ворону".
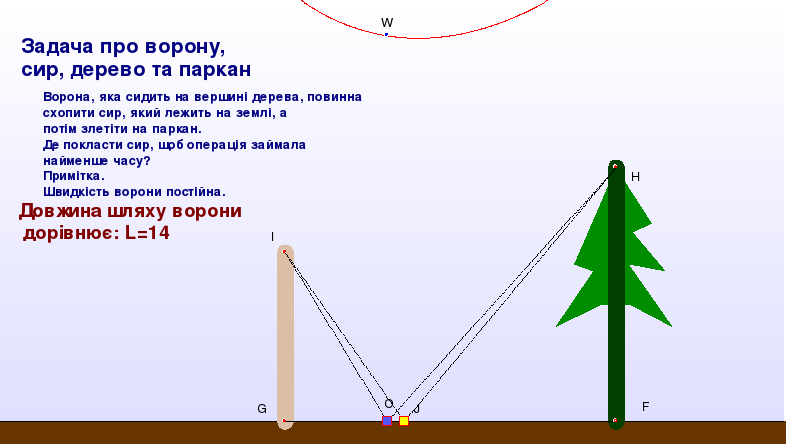
Рисунок 7.13 ДК "Задача про ворону"
Зауваження
ДК "Задача про ворону" містить графік функції, який показує залежність суми відстаней від положення точки O. Ми поки ще не обговорювали питання, як побудувати графік функції в DG, це буде зроблено далі.
1 Зауважимо, що макрос будує квадрат по одну чи іншу сторону відрізка у залежності від порядку задання кінців відрізка. Послідовності A, B і B, A призводять до побудови різних квадратів.
21 Зауважимо, що ввід параметрів функцій можна виконати напівавтоматично, клацаючи мишею відповідні точки об’єктів. Для цього кожна з функцій має свого експерта (майстра), який викликається натискуванням на стрілку справа від відповідної функції.
Просмотр содержимого документа
«08 Cartesian Coordinates»
19
71. Означення декартових координат
Знайомитися з декартовими координатами на площині найкраще за допомогою ДР “Означення декартових координат”, в якому побудовано вільну точку A, через яку проведено дві прямі, перпендикулярні до осей координат. Для того, щоб у рядку статусу відображалися координати курсору, треба встановити прапорець напроти опції Координати курсору у закладці Зовнішній вигляд програми в пункті головного меню Опції\Опції . Кількість знаків, що відображаються, можна встановити в закладці Різне — опція Точність відстаней.
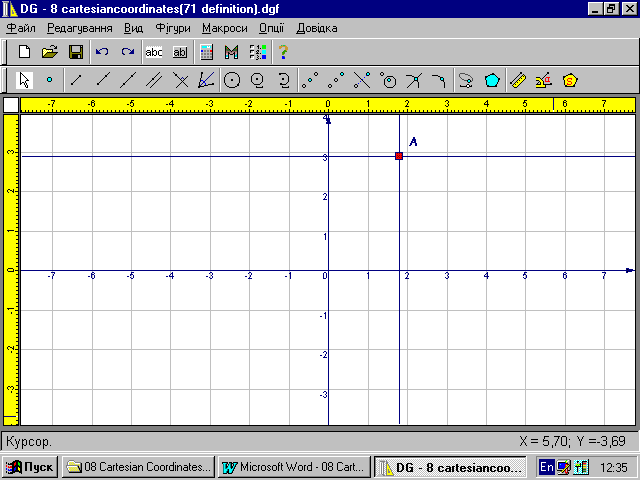
Рисунок 8.1 ДР "Означення декартових координат"
Завдання 71.1
Переміщаючи точку A у площині, дослідіть, як змінюються знаки координат точки A в залежності від квадранта.
Зауваження
Для того, щоб рухома точка прив’язувалася до вузлів координатної сітки (і, відповідно, точка рухалася стрибками — дискретно) треба переміщувати точку при натиснутій клавіші Shift.
72. Координати середини відрізка
Для дослідження координат середини відрізка можна скористатися ДР “Координати середини відрізка”, на якому побудовано відрізок AB з вільними кінцями і його середина (середину відрізка можна побудувати, наприклад, за допомогою інструмента Середина відрізка). Координати точок виведено за допомогою опції Показати координати у вікні діалогу Властивості точки, яке є контекстним вікном точки, тобто для його виклику достатньо клацнути правою кнопкою миші на точці. Точність координат (кількість знаків після десяткової точки) визначається опцією Точність чисел у закладці Різне у меню опцій пакета — Опції \ Опції.
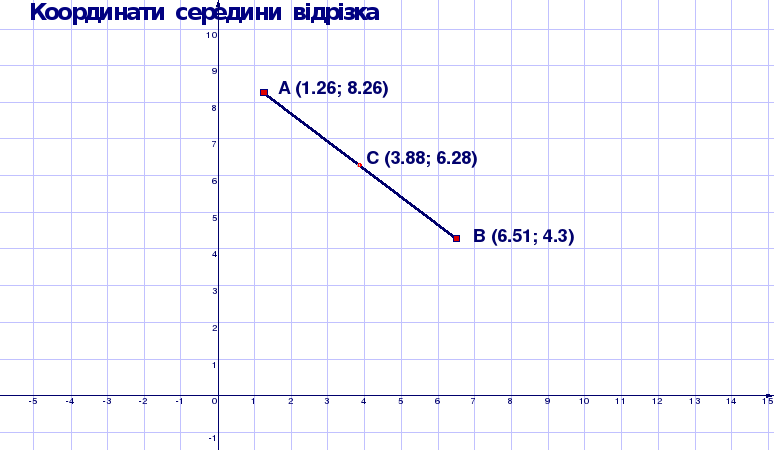
Рисунок 8.2 ДР "Координати середини відрізка"
За допомогою ДР “Координати середини відрізка” можна визначити координати середини довільного відрізка. Зауважимо, що потрібні координати вільних точок у пакеті можна встановлювати або переміщуючи точки за допомогою миші, або — аналітично, вводячи їх з клавіатури у вікні діалогу Властивості точки (див. рисунок 8.3).
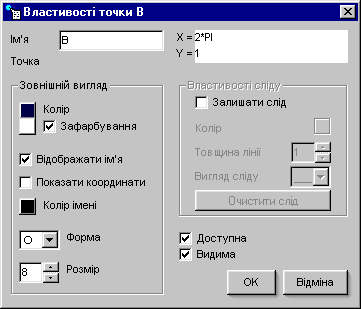
Рисунок 8.3 Ручне введення координат точок
Задача 8.13
Дано три вершини паралелограма ABCD: A(1; 0), B(2, 3), C(3, 2). Знайдіть координати четвертої вершини D і точки перетину діагоналей.
Розв’яжемо цю задачу за допомогою пакета DG.
Введемо задані три точки аналітично, скориставшись інструментом Фігури\Аналітично\Точка (тобто задаючи координати точок у режимі діалогу). Знайдемо точку перетину діагоналей — за властивостями паралелограма, це середина діагоналей. Скористаємося для цього інструментом Середина відрізка (треба активізувати цей інструмент, а потім клацнути мишею послідовно на вершині A і на вершині C).
Після цього побудуємо четверту, шукану вершину паралелограма, скориставшись для цього інструментом Симетрична точка (треба обрати цей інструмент, а потім клацнути мишею послідовно на вершині B і на точці перетину діагоналей). Для того, щоб визначити координати побудованих точок, краще підняти прапорець проти опції “Показувати координати” у вікнах діалогу “Властивості точки”, які викликаються з контекстних меню цих точок. Точність значень координат, що виводяться на екран, можна встановити в закладці “Загальні” у вікні діалогу Опції\Опції.
Після виконання побудов можна побачити, що четверта вершина паралелограма — не точка D. Для повної відповідності умовам задачі треба точки перейменувати: спочатку точку D на точку F, а потім точку E на точку F.
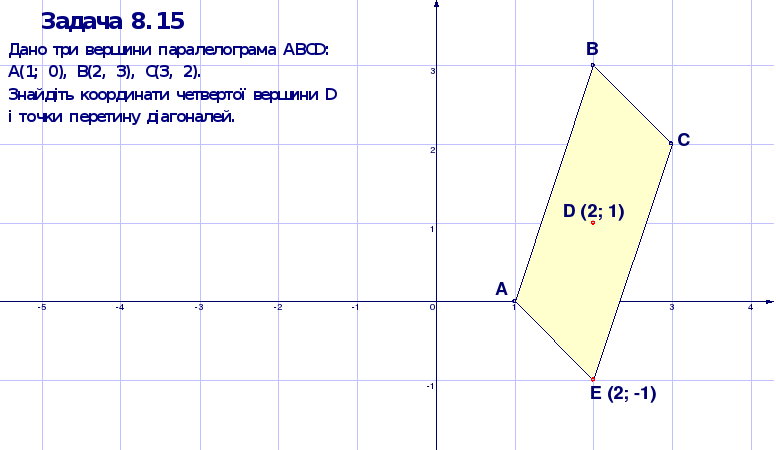
Рисунок 8.4 ДР "Четверта вершина паралелограма"
Зауваження
Ми розв’язали задачу наближено — з точністю, яку встановлено в опціях пакета. І хоч ця точність може бути достатньо високою — 10 і більше знаків після десяткової коми, все ж наближеною. Для практики в більшості випадків цього буде достатньо, для теорії — ні1.
Множина тих задач, для яких розроблені наближені методи розв’язування, значно ширша, ніж тих, для яких розроблені точні методи розв’язування.
ДР “Четверта вершина паралелограма” дозволяє в інтерактивному режимі наближено розв’язувати задачу для довільних положень вихідних точок A, B, C. Для цього достатньо переміщувати ці точки у відповідні місця на площині або ввести нові координати точок через вікна діалогу Властивості точки.
73. Відстань між точками
ДР “Відстань між точками” демонструє геометричний зміст формули для обчислення відстані між двома точками координатної площини.
Найкраще розробити цей ДР самостійно або принаймні виконати комп’ютерні експерименти — переміщувати базові точок ДР (точок A і B) та спостерігати за катетами у прямокутному трикутнику ABC (вони дорівнюватимуть проекціям відрізка AB на координатні осі).
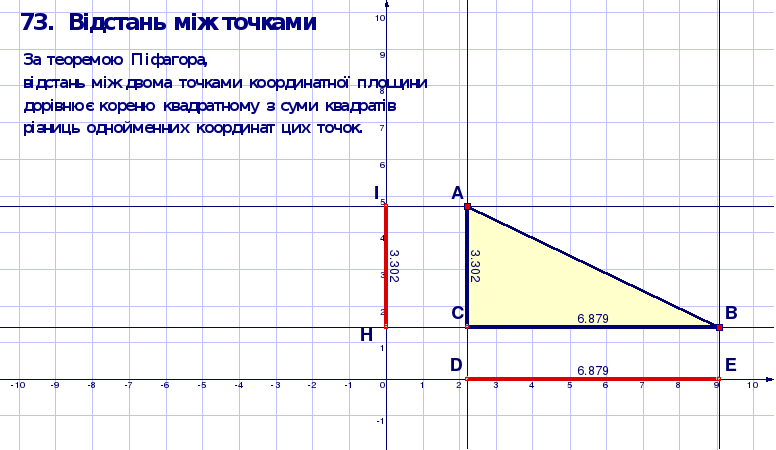
Рисунок 8.5 ДР "Відстань між точками"
Задача 73.19
Знайдіть на осі x точку, рівновіддалену від точок (1; 2) і (2; 3).
Виконайте самостійну побудову ДР “Задача 73.19” згідно з рисунком 8.6.
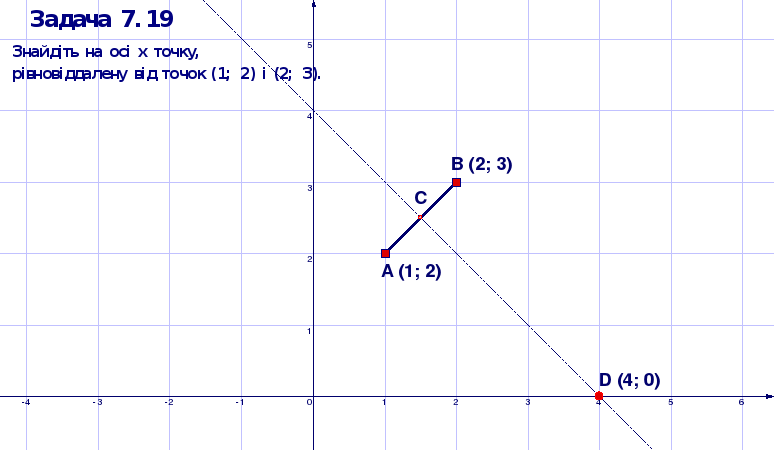
Рисунок 8.6 ДР "Задача 73.19"
Зауважимо, що за допомогою DG можна розв’язати задачу тільки наближено, проте з великою точністю. До того ж, змінюючи відповідно координати
точок A і B, за допомогою ДР “Задача 73.19” можна розв’язувати наближено задачу з будь-якими вихідними даними.
Завдання 73.1
Узагальніть ДР “Задача 73.19” так, щоб за його допомогою можна було знаходити точку, що лежить на даній прямій, рівновіддалену від двох даних точок. Дослідіть, в яких випадках ця задача не має розв’язку, коли існує єдиний розв’язок, коли розв’язків нескінченна множина.
74. Рівняння кола
До цього часу ми будували тільки коло за допомогою інструментів Коло та Коло за радіусом, не цікавлячись рівняннями побудованих кіл. Оскільки всі геометричні об’єкти в пакеті DG мають аналітичне внутрішнє представлення, то користувачеві не складно аналітично представити геометричні об’єкти. Відповідну інформацію щодо кожного об’єкта (точки, прямої, кола) можна отримати у вікні діалогу Властивості точки (відповідно Властивості точки, Властивості кола).
Завдання 74.1
Побудувати декілька кіл за допомогою інструментів пакета DG і визначити їх рівняння за допомогою вікна діалогу Властивості кола.
Обговоримо третій спосіб побудови кола — аналітичний. Для цього використовується команда головного меню Фігури\Аналітично\Коло. Після виклику цієї команди з’явиться вікно діалогу Коло аналітично (рис. 8.7). Як видно з вікна діалогу, рівняння кола можна задавати двома способами:
приведене рівняння (його ще називають канонічним рівнянням):
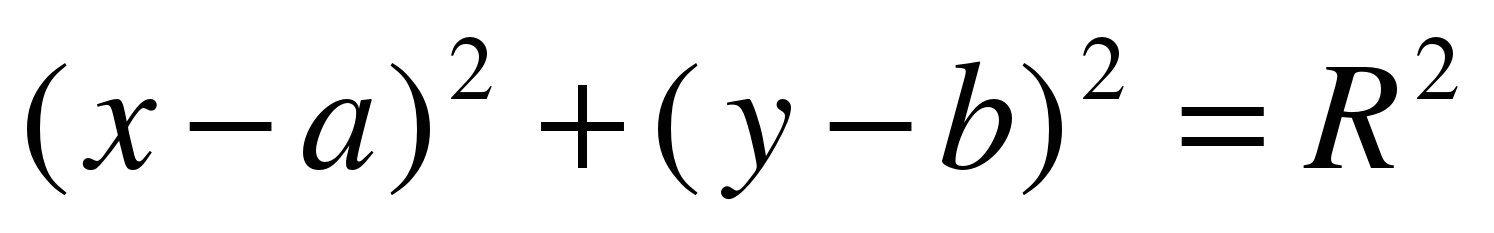 (задаються коефіцієнти
(задаються коефіцієнти 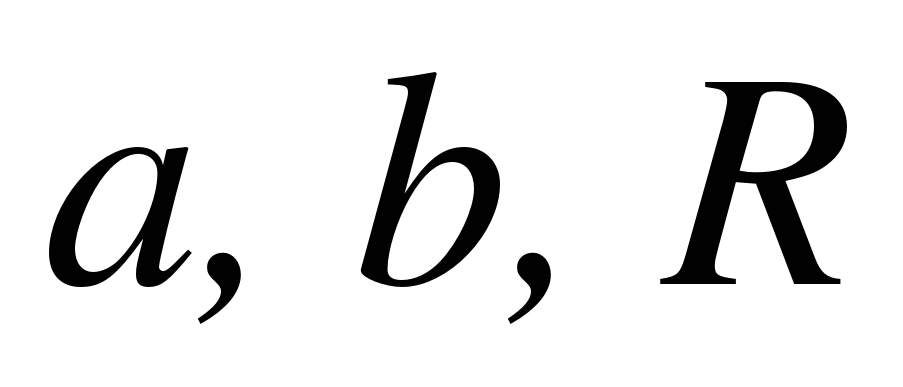 )
)загальне рівняння:
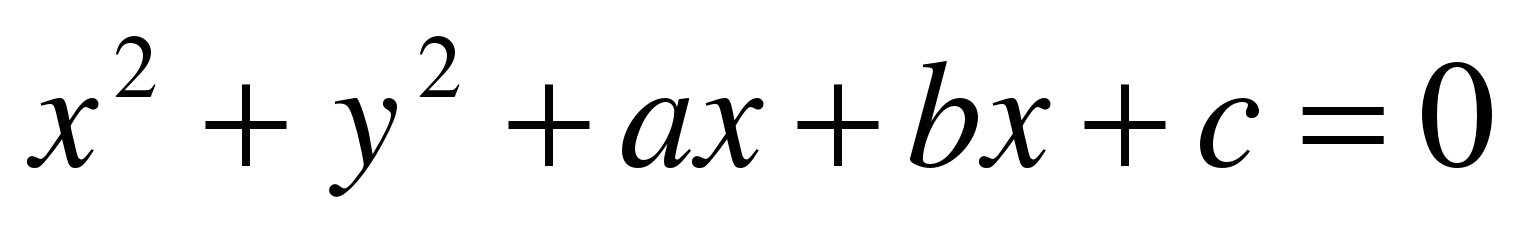 (задаються коефіцієнти
(задаються коефіцієнти 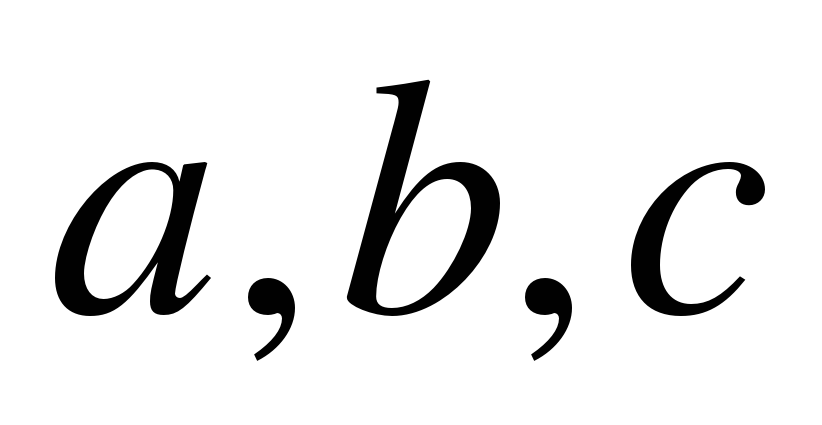 ).
).
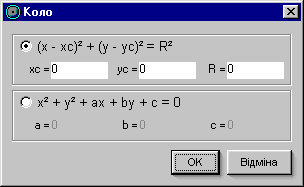
Рисунок 8.7 Вікно діалогу "Коло "
Задача 8.30.1
Визначити параметри кола, заданого рівнянням ![]() .
.
Розв’язання
Побудуємо коло, задане аналітично, скориставшись командою Фігури\Аналітично\Коло. Відповідне вікно діалогу наведено на рисунку 8.8.
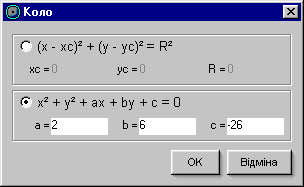
Рисунок 8.8 Задання кола за допомогою загального рівняння
Тепер достатньо побудувати коло (кнопка OK). Після побудови кола запросимо його властивості (команда Властивості контекстного меню кола). Відповідне вікно наведене на рисунку 8.9.
Таким чином, пакет DG дозволяє знаходити рівняння кола, побудованого за допомогою інструментів, і навпаки, будувати та досліджувати коло, яке задане аналітично (рівнянням у канонвчній або загальній формі).
Зауважимо також, що коло, задане аналітично, не допускає зміни своїх параметрів ні з клавіатури, ні за допомоги миші.
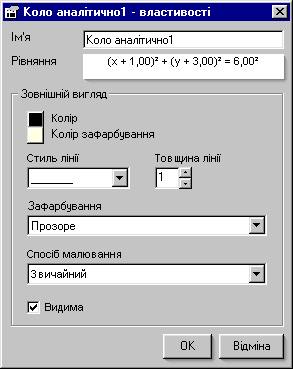
Рисунок 8.9 Канонічне рівняння кола, заданого аналітично
75. Рівняння прямої
Як було зазначено в попередньому пункті, внутрішнє представлення геометричних об’єктів в пакеті DG аналітичне, зокрема, прямі зберігаються у вигляді коефіцієнтів загального рівняння прямої ![]() , тобто трійки чисел
, тобто трійки чисел ![]() . Загальне ж рівняння прямої представлене у вікні Властивості прямої. У відповідних вікнах властивостей для променя та відрізка теж представлені загальні рівняння прямих, яким вони належать. На рисунку 8.10 наведено вікно властивостей для променя.
. Загальне ж рівняння прямої представлене у вікні Властивості прямої. У відповідних вікнах властивостей для променя та відрізка теж представлені загальні рівняння прямих, яким вони належать. На рисунку 8.10 наведено вікно властивостей для променя.
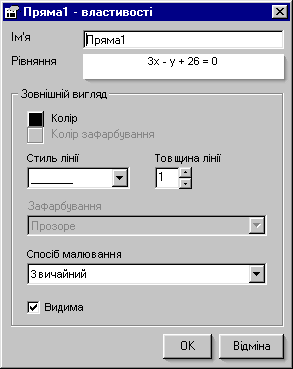
Рисунок 8.10 Рівняння прямої (променя, відрізка)
Пряму можна задати аналітично, скориставшись для цього командою Фігури\Аналітично\Пряма. До цього ж різними рівняннями, зокрема:
рівнянням з кутовим коефіцієнтом (рівняння виду
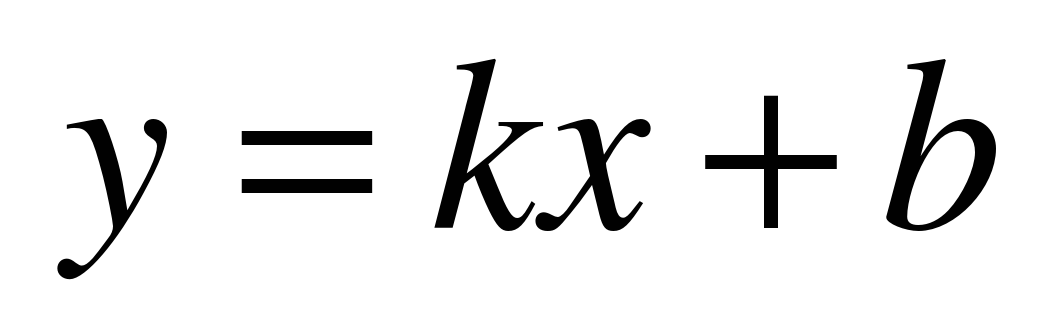 );
);загальним рівняння (рівняння виду
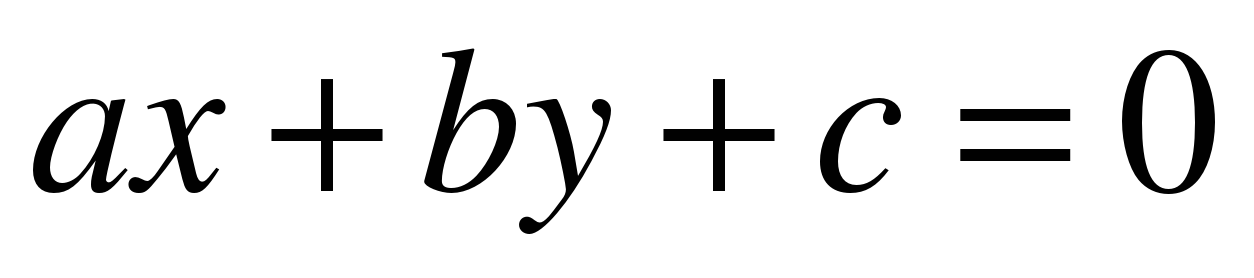 ).
).
Крім того, можна скористатися також канонічним та нормальним рівнянням прямої (зацікавлений читач може знайти обговорення цих рівнянь у будь-якому курсі аналітичної геометрії). Вікно діалогу для задання прямої аналітично, за допомогою рівняння, зображено на рисунку 8.11.

Рисунок 8.11 Аналітичне задання прямої
Зауваження
Аналітично задані прямі є повноцінними геометричними об’єктами і можуть брати участь у будь-яких побудовах. Наприклад, можна на аналітичній прямій побудувати точку або провести пряму, паралельну аналітичній прямій. Проте така пряма не має базових точок, зміною положення яких можна було б змінювати положення прямої.
Задача 8.35
Складіть рівняння прямої, яка проходить через точки A(–1; 1), B(1; 0).
Розв’язання
Побудуємо точки A і B аналітично, скориставшись командою Фігури\Аналітично\Точка. Проведемо пряму через точки A і B. Відкриємо вікно діалогу Властивості прямої, у якому буде представлене загальне рівняння прямої: ![]() .
.
Зауваження
Для розв’язування задачі можна було б побудувати пряму, яка проходить через дві довільні точки площини, перемістити базові точки прямої в задані положення, після чого прочитати у вікні властивостей рівняння шуканої прямої. Нагадуємо також, що при переміщуванні точок у площині при натиснутій клавіші Shift точка стрибає по вузлах координатної сітки, що спрощує переміщення точки в положення з цілочисельними координатами.
Координати точки перетину двох прямих можна знайти конструктивно, будуючи спочатку дві прямі, а потім їх точку перетину, координати якої можна отримати з вікна властивостей точки перетину (рис.8.12).
Рисунок 8.12 Координати точки перетину двох прямих
Задача (з тексту пункту 76 підручника)
Дві прямі задані рівняннями:
![]()
Знайти координати точки кретину цих прямих.
Розв’язання
Побудуйте дві прямі, скориставшись командою Фігури\Аналітично\Пряма.
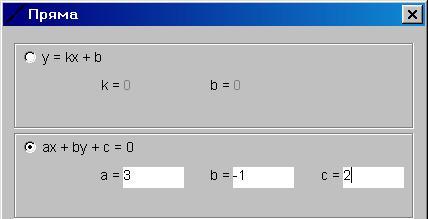
Рисунок 8.13 Задання прямої аналітично
Знайдіть точки перетину цих прямих, скориставшись інструментом Точка перетину.
Оберіть команду Властивості точки з контекстного меню точки перетину.
Отримайте координати точки перетину з вікна діалогу Властивості точки.
77. Розміщення прямої відносно системи координат
Для дослідження розміщення прямої, що задана загальним рівнянням виду ![]() відносно системи координат розробимо ДР, в якому можна, динамічно змінюючи параметри
відносно системи координат розробимо ДР, в якому можна, динамічно змінюючи параметри ![]() , спостерігати відповідні зміни в розміщенні прямої. Відразу зауважимо, що ДР буде коректно працювати тільки тоді, коли графіком рівняння дійсно буде пряма. Це відбувається, коли принаймні один із коефіцієнтів
, спостерігати відповідні зміни в розміщенні прямої. Відразу зауважимо, що ДР буде коректно працювати тільки тоді, коли графіком рівняння дійсно буде пряма. Це відбувається, коли принаймні один із коефіцієнтів ![]() або
або ![]() не дорівнює нулю. Якщо ж
не дорівнює нулю. Якщо ж ![]() , то графіком буде або вся площина (якщо
, то графіком буде або вся площина (якщо ![]() ), або порожня множина (якщо
), або порожня множина (якщо ![]() ).
).
Схема побудови ДР буде такою:
Побудувати точки для задання параметрів загального рівняння прямої. Параметри загального рівняння прямої будемо задавати положенням спеціальних точок на прямих, які будуть виконувати роль напрямних для цих точок. Таким чином, ми отримаємо три точки
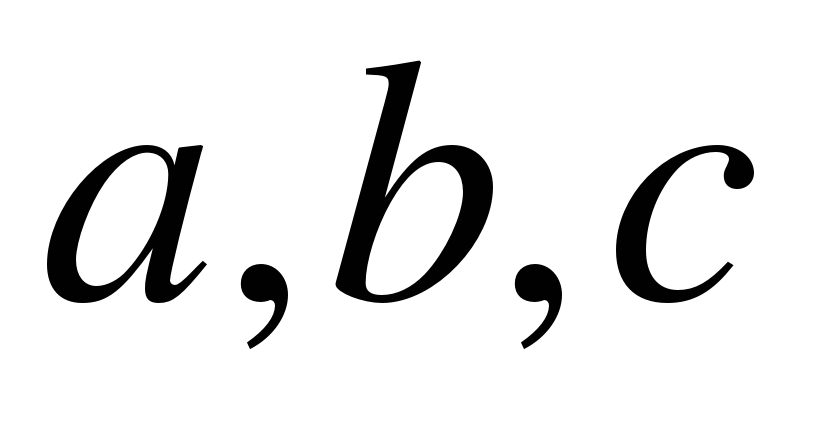 , абсциси яких ми будемо використовувати як параметри загального рівняння прямої.
, абсциси яких ми будемо використовувати як параметри загального рівняння прямої.Побудувати аналітично дві точки, які визначать положення прямої. Труднощі виникають тому, що аналітичні формули, які визначають координати цих двох точок, різні у залежності від того, чи дорівнює коефіцієнт
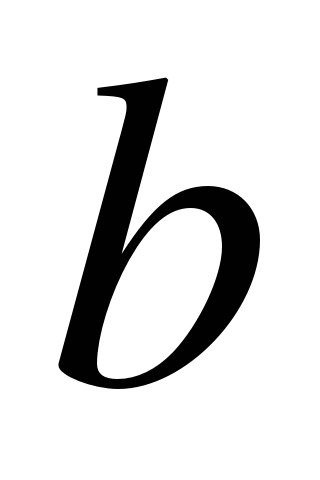 нулю, чи ні. Ці точки можна обирати різними
нулю, чи ні. Ці точки можна обирати різними
способами. Ми задамо точки за наступними формулами2: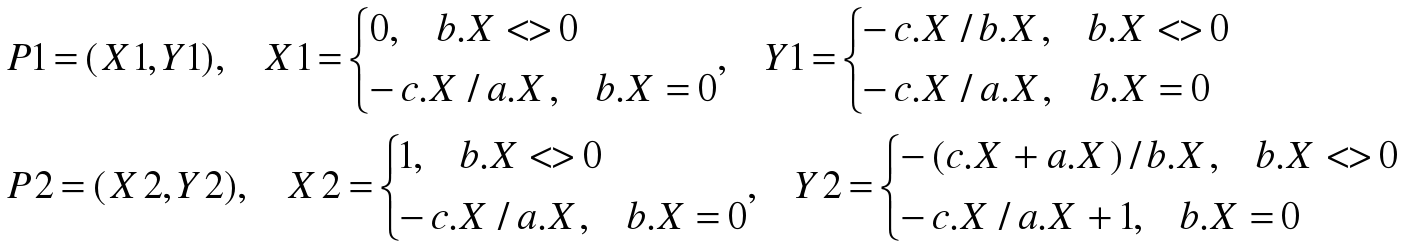
Нагадаємо, що в пакеті DG абсциси точок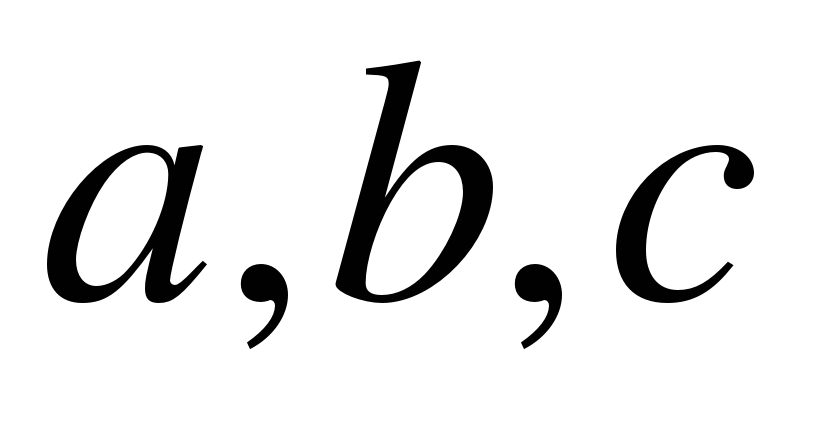 зберігаються у змінних
зберігаються у змінних 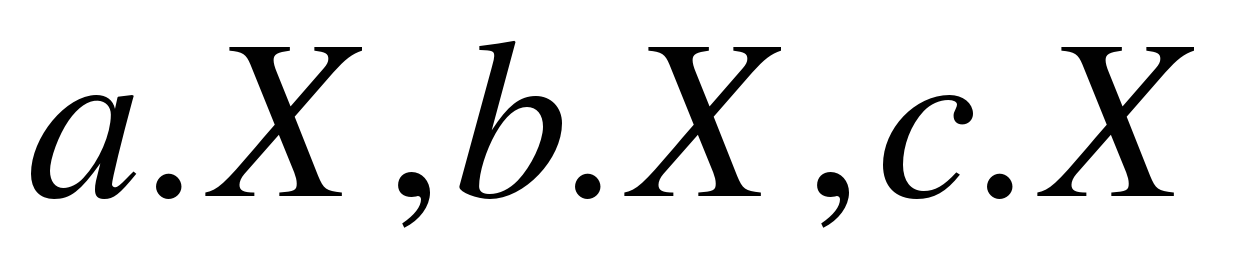 , ординати —
, ординати — 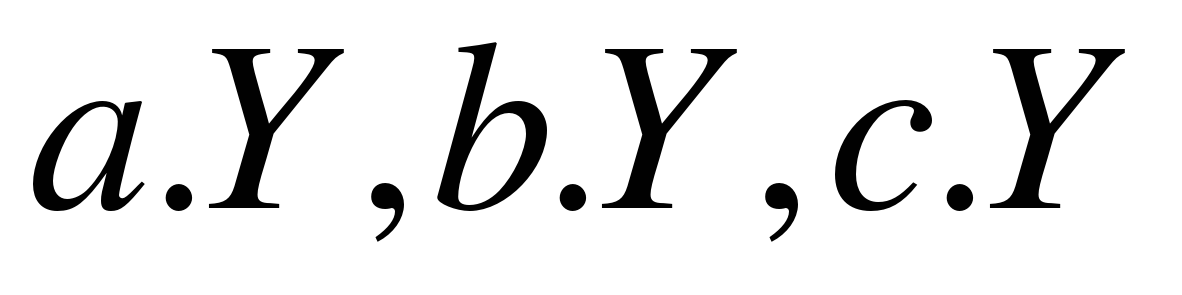 . Для того, щоб наведені вище формули ввести для визначення координат аналітичних точок, потрібна умовна функція — функція if(Умова, Вираз1, Вираз2)), яка обчислює значення виразів (Вираз1 або Вираз2) у залежності від того, чи виконується умова Умова . Наприклад, функцію для обчислення модуля числа можна у синтаксисі пакета DG записати у вигляді
. Для того, щоб наведені вище формули ввести для визначення координат аналітичних точок, потрібна умовна функція — функція if(Умова, Вираз1, Вираз2)), яка обчислює значення виразів (Вираз1 або Вираз2) у залежності від того, чи виконується умова Умова . Наприклад, функцію для обчислення модуля числа можна у синтаксисі пакета DG записати у вигляді 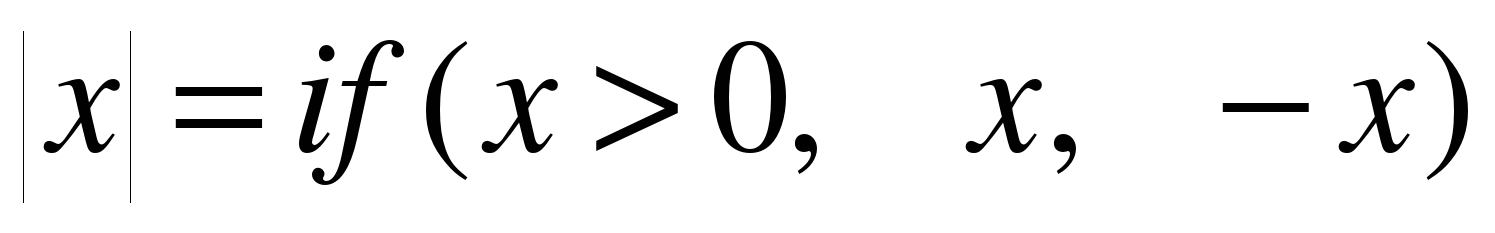 . Введення координат аналітичних точок можна побачити на наступному рисунку.
. Введення координат аналітичних точок можна побачити на наступному рисунку.
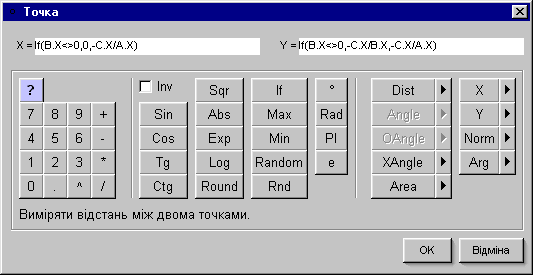
Рисунок 8.14 Введення виразів аналітичних точок
Побудувати пряму, яка проходить через дві аналітичні точки;
Побудувати динамічні надписи для виведення значень параметрів та рівняння прямої;
Побудувати надпис з завданням дослідження;
Створити кнопку Дослідження, натисненням на яку можна сховати або відобразити завдання дослідження.
Зауваження
Хід побудови ДР можна простежити при покроковому виконанні побудови, скориставшись командою Вид\Покрокове відтворення побудови.
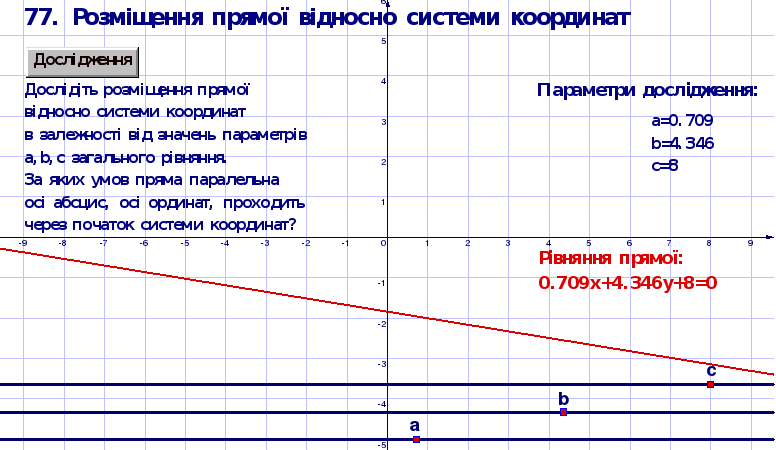
Рисунок 8.15 ДР "Розміщення прямої відносно системи координат"
Задача 77.43
Складіть рівняння прямої, яка паралельна осі x і проходить через
точку (2; 3).
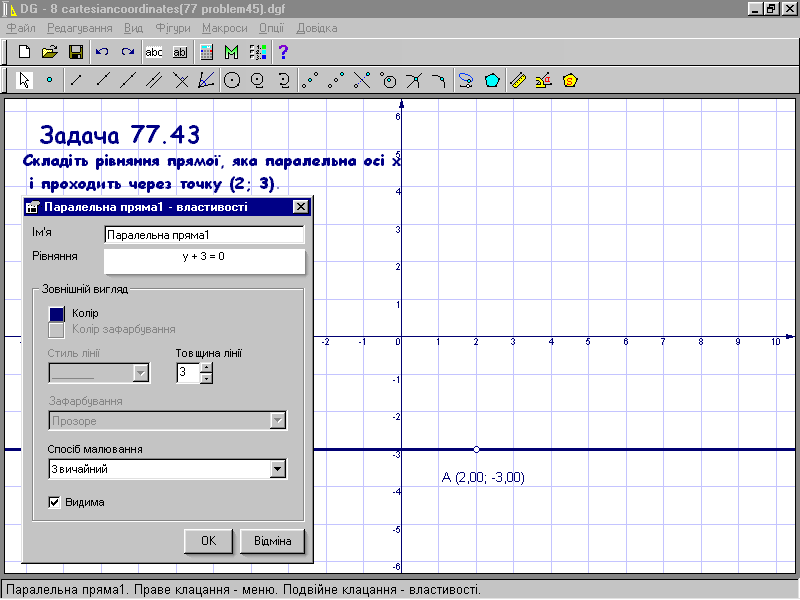
Рисунок 8.16 ДР “Задача 77.43”
Розв’язання
Розв’язати задачу можна в середовищі пакета DG так (рис. 8.16):
Побудуйте точку з заданими координатами;
Побудуйте шукану пряму, скориставшись інструментом Паралельна пряма;
Отримайте рівняння шуканої прямої, скориставшись вікном Властивості прямої, яке викликається з контекстного меню прямої.
Зауваження
Наголосимо, що ми отримали ДР для розв’язування в інтерактивному режимі задачі для будь-якої точки на площині. Це важлива сторона розв’язування задач у середовищі пакета DG: розв’язування конкретної задачі дає завжди розв’язування цілого класу задач. Загальність розв’язання є результатом винахідливості та творчої вдачі автора.
78. Кутовий коефіцієнт у рівнянні прямої
Рекомендуємо сконструювати самостійно ДР для дослідження геометричного змісту коефіцієнтів рівняння прямої з кутовим коефіцієнтом (рівняння виду ![]() ). Зображення ДР можна знайти на рисунку 8.17, послідовність його розробки можна простежити скориставшись послугою покрокової демонстрації Вид\Покрокове відтворення побудови.
). Зображення ДР можна знайти на рисунку 8.17, послідовність його розробки можна простежити скориставшись послугою покрокової демонстрації Вид\Покрокове відтворення побудови.
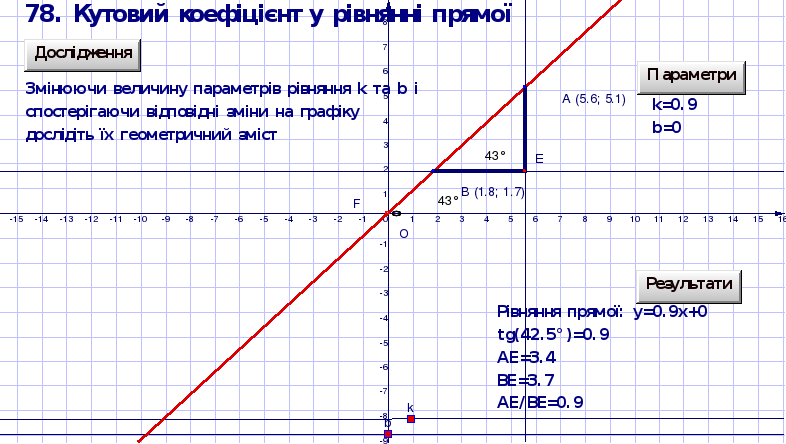
Рисунок 8.17 ДР “Кутовий коефіцієнт прямої”
80. Перетин прямої з колом
Розробимо ДР для дослідження умов, за яких пряма перетинається з колом і за яких точок перетину буде дві, одна або не буде жодної.
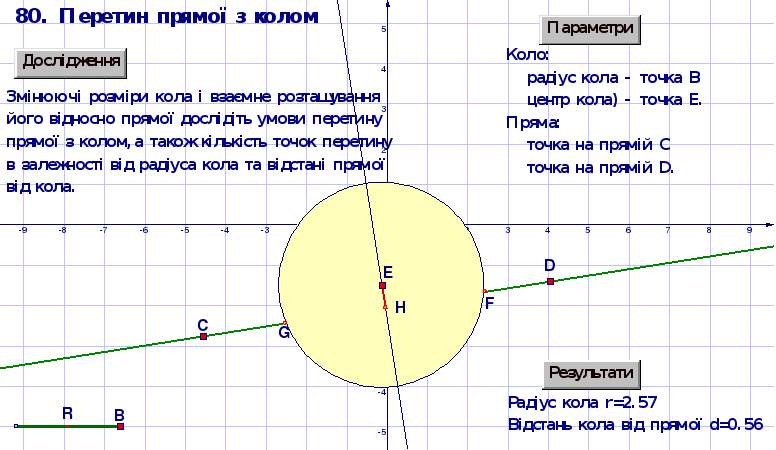
Рисунок 8.18 ДР "Перетин прямої з колом"
ДР розробляється стандартними прийомами, які вже не раз було обговорено. Крім того можна простежити послідовність авторської розробки, виконуючи покрокову побудову (команда Вид\Покрокове відтворення побудови).
1 У майбутньому планується подолання цього недоліку в пакеті DG. Для цього треба поповнити пакет можливостями точних та символьних обчислень. Однак жоден пакет динамічної геометрії поки що таких можливостей не має.
2 Ми використовуємо знак ![]() як
як ![]() для того, щоб легше сприймалося наступне обговорення задання координат аналітичних точок у пакеті DG.
для того, щоб легше сприймалося наступне обговорення задання координат аналітичних точок у пакеті DG.
Просмотр содержимого документа
«09 Movies»
22
82. Перетворення фігур
Геометричні перетворення — дуже важливий розділ курсу геометрії. Більш за те, у 19 сторіччі математики зрозуміли1, що єдиний погляд на всі геометрії2 можливий з точки зору того, які множини перетворень розглядаються як ті, що не змінюють властивості геометричних фігур. Так, у геометрії Евкліда, яку ми вивчаємо, досліджуються ті властивості геометричних фігур, які не змінюються при рухах фігур (образно кажучи, кожну геометричну фігуру можна розглядати як “тверду”, наприклад, вирізану з картону, і нас цікавлять ті властивості цієї фігури, які не змінюються при зміні її положення). Для кожної з геометрій існує деяка множина геометричних перетворень і у цій геометрії вивчаються ті властивості фігур, які не змінюються при цих перетвореннях. Такий погляд не тільки дозволив навести деякий порядок серед розмаїття створених геометрій, але і пролив світло на кожну геометрію, зокрема, дозволив впорядкувати зміст кожної з геометрій, стимулював нові дослідження. Більш за те, метод геометричних перетворень став найголовнішим та найпродуктивнішим методом як побудови геометрій, так і розв’язування геометричних задач. Математична теорія симетрії, симетрія у живій та неживій природі, мистецтві, архітектурі, інженерії отримали спільне підґрунтя у геометричних перетвореннях3. Ідеї геометричних перетворень дуже природні. Між тим, ці теми важко входять у педагогічну практику, особливо у викладання математики в школі. Можливо, брак годин, а також обмеженість наочності викликає ці труднощі. Ми сподіваємось, що можливості пакета DG у виконанні геометричних перетворень сприяє тому, що ви відчуєте красу і міць методів геометричних перетворень.
Для засвоєння різних типів геометричних перетворень ми пропонуємо таку загальну схему:
Практичне ознайомлення з дією перетворення на точку на основі комп’ютерних експериментів у пакеті DG, тобто практичне ознайомлення з означенням геометричного перетворення;
Практичне ознайомлення з дією перетворення на геометричні примітиви (пряму, промінь, відрізок, коло) на основі комп’ютерних експериментів у пакеті DG;
Практичне ознайомлення з дією перетворення на многокутники на основі комп’ютерних експериментів у пакеті DG;
Розв’язування задач у середовищі пакета DG з використанням методу геометричних перетворень.
Почнемо з загального означення геометричного перетворення.
Геометричне перетворення фігури — це відображення кожної точки геометричної фігури у визначену яким-небудь чином іншу точку площини.
Зауважимо, що роль геометричної фігури може виконувати сама площина. У подальшому ми будемо розглядати перетворення площини.
Розробимо ДР “Перетворення фігур”.
Почніть конструювання нового ДР, скориставшись інструментом Створити новий рисунок;
Збережіть ДР на диску, скориставшись командою Файл\Зберегти;
Побудуйте дві точки A та B, скориставшись інструментом Точка
(до точки A будемо застосовувати геометричне перетворення, координати точки B будуть виконувати роль параметрів геометричного перетворення);Побудуйте аналітичну точку C, скориставшись інструментом Фігури\Аналітично\Точка. У вікні діалогу Точка введіть координати аналітичної точки за формулами: X=A.X+B.X, Y=A.Y+B.Y
(формули відповідають перетворенню паралельного перенесення на вектор OB; паралельне перенесення буде систематично вивчатися в рамках даної теми у п. 87);Встановіть властивості точки A, скориставшись вікном діалогу Властивості точки:
Зовнішній вигляд (форма, розмір, заливка, показати координати);
Властивості сліду (створювати слід, колір, товщина лінії);
Встановіть властивості точки C, скориставшись вікном діалогу Властивості точки:
Зовнішній вигляд (форма, розмір, заливка, показати координати);
Властивості сліду (створювати слід, колір, товщина лінії);
У результаті ми повинні отримати ДР, який відповідає рисунку 9.1.
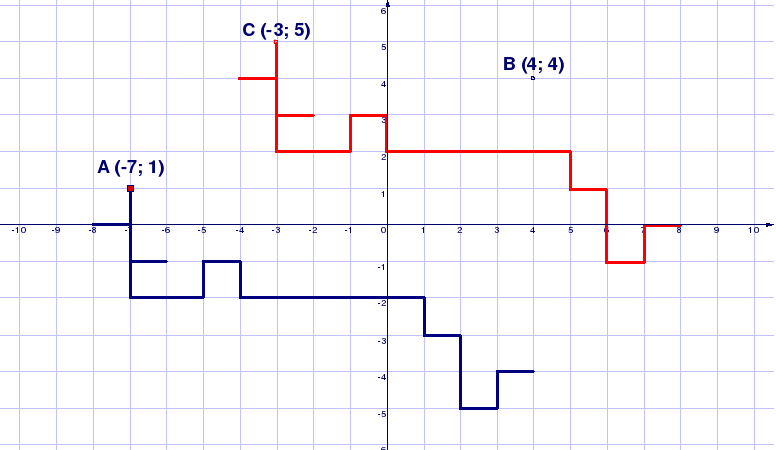
Рисунок 9. 1 ДР "Перетворення фігур"
Тепер можна виконувати комп’ютерні експерименти з цим перетворенням.
Будемо реалізовувати наведену вище схему.
Комп’ютерні експерименти з ДР “Геометричні перетворення”
Дослідіть дію перетворення на точку:
Переміщуйте точку A за допомогою миші і спостерігайте:
За лініями, які при цьому утворюються слідами точок A і C ;
За координатами рухомих точок A і C;
Вилучіть сліди точок A і C, скориставшись командою Вилучити слід (цю команду можна вибрати або у контекстному меню точок або у вікнах діалогу Властивості цих точок);
Переміщуйте точку B за допомогою миші і спостерігайте:
За лініями, які при цьому утворюються слідами точок B і C ;
За координатами рухомих точок B і C;
Повторіть пункти 1.1 та 1.2 з натиснутою клавішею Shift — приклад відповідного екрана наведено на рисунку 9.1.
Зробіть висновки щодо дії на точку паралельного перенесення.
Дослідіть дію перетворення на геометричні примітиви
(пряму, промінь, відрізок, коло):
2.1.Побудуйте геометричні примітиви (пряму, промінь, відрізок, коло); після цього ДР прийме вигляд, який відповідає наступному рисунку 9.2.
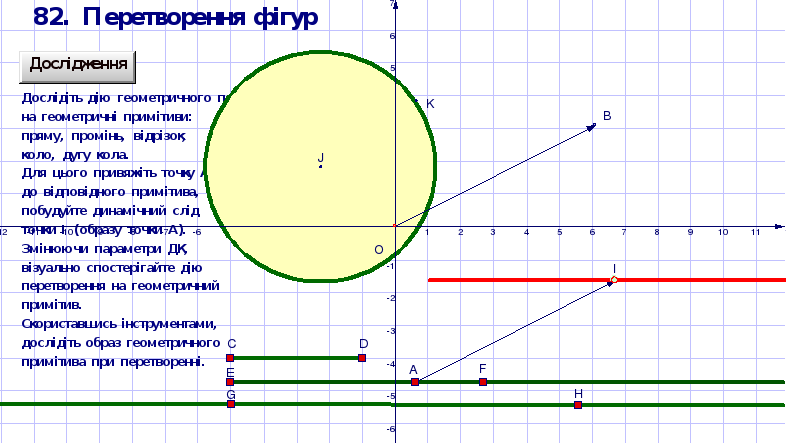
Рисунок 9.2 ДР "Дія перетворення на геометричні примітиви"
2.2.Дослідіть дію перетворення на пряму, скориставшись інструментом Динамічний слід:
2.2.1.Підведіть точку A до прямої;
2.2.2.Пристебніть точку A до прямої, скориставшись командою Пристебнути до фігури з контекстного меню точки A;
2.2.3.Побудуйте динамічний слід точки A, скориставшись інструментом Динамічний слід:
2.2.3.1.Вибрати інструмент Динамічний слід на панелі геометричних інструментів і клацнути спочатку на точці A, а потім — на
точці B;
2.2.4.Дослідіть дію перетворення на пряму, змінюючи положення точок A і B;
2.3. Дослідіть дію перетворення на промінь (аналогічно пункту 2.2 дослідження дії перетворення на пряму);
2.4. Дослідіть дію перетворення на відрізок (аналогічно пункту 2.2 дослідження дії перетворення на пряму);
2.5. Дослідіть дію перетворення на коло (аналогічно пункту 2.2 дослідження дії перетворення на пряму);
2.6. Зробіть висновки щодо дії паралельного перенесення на геометричні примітиви;
2.7. Проведіть комп’ютерні експерименти з іншими геометричними перетвореннями (для цього аналітичну точку C треба задати іншими формулами, наприклад, X=A.X*B.X, Y=A.Y*B.Y .
Як приклад цікавого перетворення площини, наведемо приклад перетворення інверсії. Перетворення інверсії не вивчається за програмою шкільного курсу, але це важливе і цікаве перетворення, і тому ми пропонуємо “пограти” з інверсією за допомогою ДР, який наведено нижче.
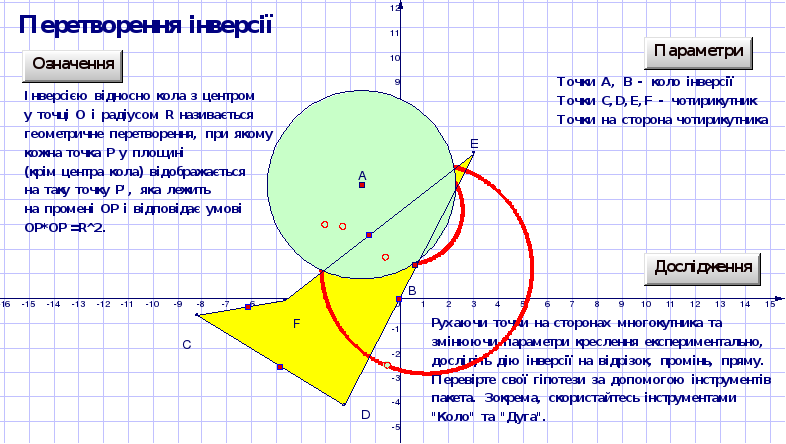
Рисунок 9.3 ДР "Дослідження властивостей інверсії"
Перетворення інверсії не є рухом, це теж важливо, бо може скластися враження, що всі геометричні перетворення — рухи. На відміну від рухів інверсія не обов’язково перетворює пряму в пряму, а коло в коло, але прямі і кола переходять або у прямі, або у кола. Докладніше можна це дослідити експериментально за допомогою ДР "Дослідження властивостей інверсії".
З виразних прикладів використання інверсії можна навести приклад відомої задачі Аполонія.
Задача Аполонія
Побудувати коло, яке дотикається трьох даних кіл.
Цю задачу було досліджено і розв’язано давньогрецьким математиком Аполонієм за допомогою циркуля та лінійки за допомогою більше 500 кроків (якщо за крок будемо вважати операцію проведення прямої за двома точками, операцію побудови кола за даним радіусом і центром кола та знаходження точки перетину двох ліній (двох прямих, двох кіл або кола і прямої). Якщо вважати за допустиму операцію побудову інверсної точки, інверсного образа кола та інверсного образа прямої, то коло Аполонія можна побудувати за 45 кроків.
Загальна схема розв’язання задачі Аполонія така:
Обрати з трьох заданих кіл коло найменшого радіусу, нехай його радіус буде дорівнювати r (не більше 4 операцій).
Побудувати три кола, які будуть концентричні вихідним колам, радіуси яких зменшені на r (при цьому найменше коло перетвориться на точку, яку позначимо через O) (не більше 12 операцій).
Побудувати довільне коло з центром у точці O і довільним радіусом, наприклад, радіусом r — коло інверсії (1 операція).
Побудувати інверсні образи побудованих кіл (у випадку, коли коло не проходить через центр інверсії його образом буде коло, у протилежному випадку — пряма) (2 операції).
Побудувати спільну дотичну до побудованих кіл — образів вихідних кіл (не більше 21 операцій).
Побудувати інверсний образ спільної дотичної (1 операція).
Побудувати коло, концентричне образу спільної дотичної, радіус якого збільшений на r — це і буде шукане коло (4 операції).ї
Зауважимо також, що серед інструментів пакета DG є інструмент Інверсна точка. Для побудови інверсної точки відносно заданого кола треба клацнути мишею на колі, а потім на точці (або навпаки — спочатку на точці, а потім на колі інверсії).
Завдання 9.82.1 (підвищеної складності)
Створіть макрос для побудови образу кола при інверсії (неособливий випадок — коли коло не проходить через центр кола інверсії).
Зауважимо, що образ такого кола є коло, проте центр кола не переходить у центр інверсного кола. (Цей макрос забезпечить напівавтоматичне виконання пункту 4).Створіть макрос для побудови образу прямої (неособливий випадок —коли пряма не проходить через центр інверсії). (Цей макрос забезпечить напівавтоматичне виконання пункту 6).
Створіть макрос для побудови кола Аполлонія для трьох заданих кіл.
Завдання 82.2
Побудуйте ДР “Афінні перетворення” для експериментального дослідження властивостей перетворень площини, які задаються формулами:
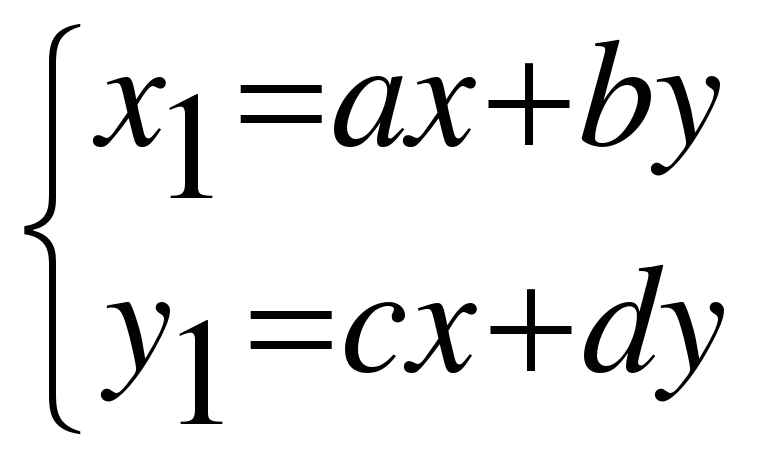
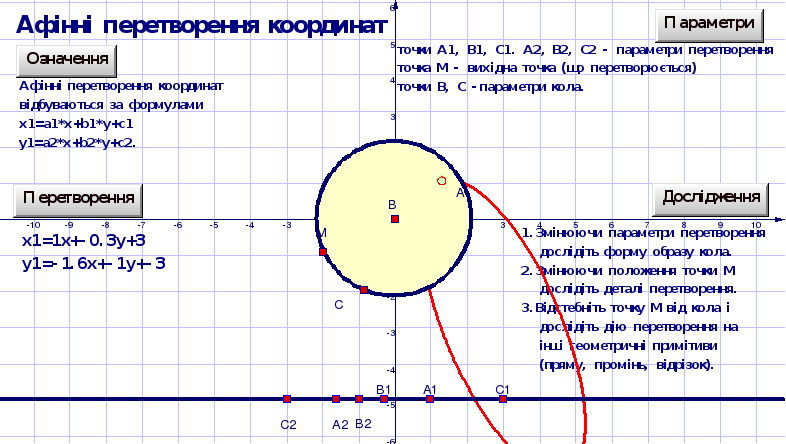
Рисунок 9. 4 ДР "Афінні перетворення"
Зауваження
Усі рухи площини є афінними перетвореннями, тобто усі види рухів, які будуть вивчатись у курсі геометрії є окремими випадками афінних перетворень. Більш за те, усі перетворення подібності, які також будуть вивчатися у даному курсі пізніше є афінними перетвореннями. Не всі перетворення афінні — перетворення інверсії не є афінним перетворенням. Афінні перетворення вивчаються в університетському курсі аналітичної геометрії.
84. Симетрія відносно точки
Для дослідження властивостей перетворення симетрії відносно точки підготуємо ДР “Дослідження перетворення симетрії відносно точки” згідно рисунку 9.5. Не будемо обговорювати детально процес розробки цього ДР — він аналогічний розробці ДР "Дія перетворення на геометричні примітиви". Виняток складає тільки дія симетрії на многокутник, у нашому випадку — шестикутник, на чому ми і зупинимось.
Побудова ДР “Дослідження перетворення симетрії відносно точки”
Побудуйте елементи ДР для дослідження дії перетворення симетрії на геометричні примітиви аналогічно побудовам ДР “Дія перетворення на геометричні примітиви".
Побудуйте елементи ДР для дослідження дії перетворення симетрії на многокутник:
Побудуйте многокутник, скориставшись для цього інструментом Многокутник;
Побудуйте образи вершин многокутника при центральній симетрії, скориставшись інструментом Симетрична точка;
Побудуйте образ многокутника, скориставшись інструментом Многокутник.
Зауваження
Твердження, що образом многокутника при центральній симетрії є многокутник, утворений образами вершин вихідного многокутника, випливає з того, що центральна симетрія є рух. Звідси випливає, що образом відрізка прямої є відрізок прямої тієї ж довжини, образом трикутника — рівний йому трикутник, образом многокутника — рівний йому многокутник.
Завдання 9.84.1
Проведіть комп’ютерні експерименти з ДР “Дослідження перетворення симетрії відносно точки”
Дослідіть дію перетворення на точку:
Переміщуйте точку A за допомогою миші і спостерігайте:
За лініями, які при цьому утворюються слідами точок A і B ;
За координатами рухомих точок A і B;
Вилучіть сліди точок A і B, скориставшись командою Вилучити слід (цю команду можна вибрати або у контекстному меню цих точок, або у вікнах діалогу Властивості цих точок);
Переміщуйте точку O за допомогою миші і спостерігайте:
За лініями, які при цьому утворюються слідами точок O і B ;
За координатами рухомих точок O і B;
Повторіть пункти 1.1 та 1.3 з натиснутою клавішею Shift;
Дослідіть перетворення координат при симетрії відносно початку системи координат:
Перемістіть центр симетрії (точку O) у початок системи координат (для спрощення переміщення виконуйте з натиснутою клавішею Shift);
Переміщуйте за допомогою миші точку A і спостерігайте за зміною координат точок A і B;
Зробіть висновки щодо перетворення координат точки при симетрії відносно початку координат;
Дослідіть перетворення координат точки при симетрії відносно довільної точки.
Зробіть висновки щодо дії на точку перетворення симетрії відносно точки.
Дослідіть дію симетрії відносно точки на геометричні примітиви
(пряму, промінь, відрізок, многокутник, коло):Побудуйте геометричні примітиви (пряму, промінь, відрізок, коло);
після цього ДР прийме вигляд, який відповідає рисунку 9.5.
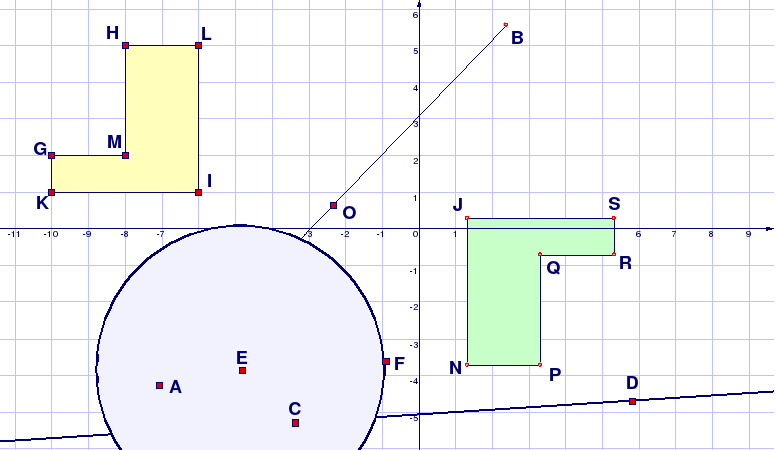
Рисунок 9.5 ДР "Дослідження симетрії відносно точки"
Дослідіть дію симетрії відносно точки на пряму, скориставшись інструментом Динамічний слід:
Підведіть точку A до прямої;
Пристебніть точку A до прямої, скориставшись командою Пристебнути до фігури з контекстного меню точки A;
Побудуйте динамічний слід точки B, скориставшись інструментом Динамічний слід:
Виберіть інструмент Динамічний слід на панелі геометричних інструментів, клацніть спочатку на точці A, а потім —на точці B;
Дослідіть дію симетрії відносно точки на пряму, змінюючи положення точок A та O;
Дослідіть дію симетрії відносно точки на промінь (аналогічно пункту 2.2 дослідження дії перетворення на пряму);
Дослідіть дію симетрії відносно точки на відрізок(аналогічно пункту 2.2 дослідження дії перетворення на пряму);
Дослідіть дію симетрії відносно точки на коло (аналогічно пункту 2.2 дослідження дії перетворення на пряму);
Дослідіть дію симетрії відносно точки на многокутник (аналогічно пункту 2.2 дослідження дії перетворення на пряму);
Зробіть висновки щодо дії симетрії відносно точки на геометричні примітиви.
Розглянемо використання центральної симетрії для розв’язування задач.
Задача 74.10
Дано прямі, які перетинаються, і точка, що не лежить на цих прямих. Побудуйте відрізок з кінцями на даних прямих і серединою в даній точці.
Розв’язок цієї задачі у загальному вигляді подано на наступному рисунку.
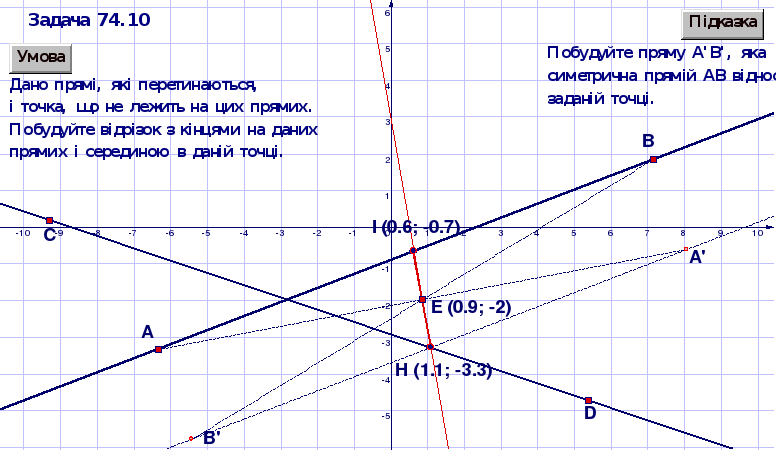
Рисунок 9.6 ДР "Задача 74.10"
Вимірюваннями елементів можна експериментально впевнитись, що побудований відрізок —шуканий.
Доведення правильності знайденого розв’язку очевидне — кінці відрізка симетричні відносно заданої точки E за побудовою.
Дослідження розв’язку — за яких умов, скільки розв’язків має задача теж не викликає труднощів. Якщо вихідні прямі перетинались, то пряма, симетрична до однієї із прямих має єдину точку перетину з другою прямою, а отже, розв’язок завжди існує і єдиний.
Залишається тільки одне питання — а як до такого розв’язку можна дійти самостійно, звідки виникло бажання побудувати симетричну пряму? Визначеної відповіді на це питання немає і бути не може — доведено, що універсальних правил знаходження розв’язків задач не існує, це — алгоритмічно нерозв’язна задача. Проте, ми говорили, що перетворення відіграють центральну роль у побудові геометрії, перетворення — один з найпродуктивніших методів геометрії. І тому, якщо в умовах задачі фігурує точка і якийсь елемент задачі симетричний відносно неї (у нашому випадку — шуканий відрізок), то цілком природно поекспериментувати з перетворенням симетрії відносно заданої точки.
Завдання 9.84.2
Сформулюйте задачі, аналогічні задачі 74.10, в яких одна чи обидві прямі замінені на кола.
Побудуйте ДР для розв’язування сформульованих задач.
Дослідіть отримані розв’язки експериментально.
Доведіть дедуктивно правильність розв’язків, виконайте дослідження умов, за яких задачі мають розв’язки.
85. Симетрія відносно прямої
Для дослідження дії симетрії відносно прямої на геометричні примітиви та многокутники сконструюйте ДР “Симетрія відносно прямої”. Ми не будемо обговорювати деталі побудови цього ДР — він цілком аналогічний побудові ДР “Симетрія відносно точки”. Наведемо зображення варіанта такого ДР (зрозуміло, ДР можна запустити клацнувши мишкою на зображенні, якщо ви користуєтесь електронним варіантом тексту, або запустивши його з CD- диску).
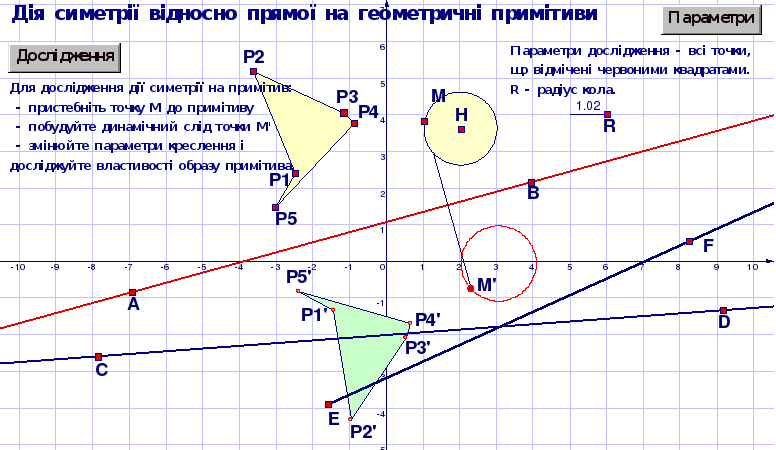
Рисунок 9.7 ДР "Дія симетрії відносно прямої на примітиви"
Завдання 9.85.1
Самостійно побудуйте ДР для дослідження та наближеного розв’язування задачі 9.24, умову якої наведено нижче. (Вказівка: скористайтеся симетрією відносно прямої).
Задача 9.24
Дано три прямі a, b, c, які попарно перетинаються. Як побудувати відрізок, перпендикулярний до прямої b, середина якого лежить на прямій b, а кінці на прямих a і c. Чи завжди задача має розв’язок?
86. Поворот
Для дослідження властивостей повороту підготуємо ДР “Дослідження властивостей повороту”, згідно з наведеним нижче рисунком.
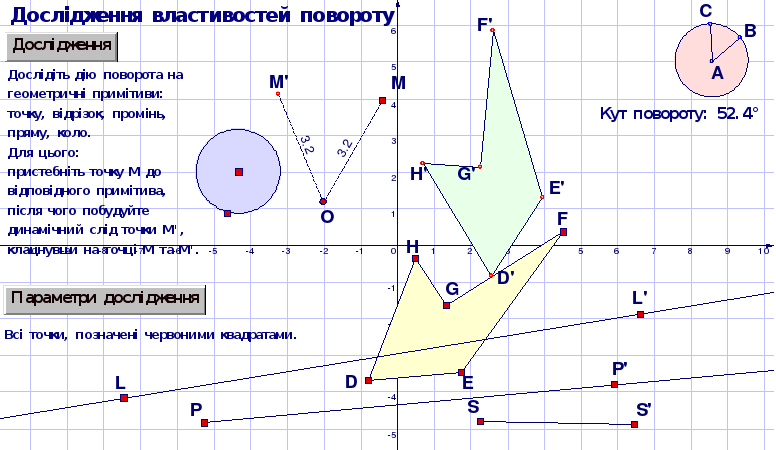
Рисунок 9.8 ДР "Дослідження властивостей повороту"
Розробка ДР не потребує на особливі коментарі. Він розробляється за тією ж схемою, що і ДР для досліджень властивостей симетрії відносно точки та симетрії відносно прямої. Єдина трудність полягає у тому, що операції Повернути точку немає серед стандартних інструментів DG. Це не біда — розробимо відповідний макрос Rotate. Ми пам’ятаємо, що все, що можна побудувати за допомогою циркуля та лінійки — можна побудувати в DG. Побудову цього макросу обговоримо у кінці розділу, а для підготовки ДР можна скористатися готовим макросом Rotate, який зберігається у папці PupilGuide\9 Movies\9 Movies(DGF). Нагадаємо, що для завантаження макросу треба виконати команду Макроси\Завантажити макроси. Для використання макросу треба вибрати команду Макроси\Rotate, після чого вказати параметри макросу:
Центр повороту;
Кут (як звичайно, трьома точкам: точка на стороні, вершина, точка на стороні, у напрямку проти годинникової стрілки);
Точку (яку слід повертати).
Дослідження властивостей повороту виконайте згідно тексту, наведеного на зображенні ДР.
Побудова макросу Rotate повороту точки відносно заданої точки на заданий кут
Почніть новий ДР;
Побудуйте три точки A, B, C, які визначають кут повороту;
Побудуйте центр повороту — точку D;
Побудуйте точку E (на яку буде діяти поворот);
Побудуйте аналітичну точку F, скориставшись командою Фігури\Аналітично\Точка і задавши координати точки виразами:
X=D.X+DE*cos(Xangle(D,E4)+OAngle(A,B,C))
Y=D.Y+DE*sin(Xangle(D,E)+OAngle(A,B,C));Виберіть команду Макроси\Створити макрос;
Укажіть вихідні параметри макросу (точки D, A, B, C, E);
Виберіть команду Завершити ввід вхідних даних на панелі створення макросу (наступна за стандартною панеллю);
Укажіть результуючі параметри макросу — точку F;
Скоригуйте, якщо в цьому є потреба, підказки пакета у рядку статусу при вводі параметрів макросу.
Збережіть макрос у бажаному місці, скориставшись для цього відповідним вікном діалогу.
Проведіть тестування розробленого макросу.
Завдання 9.86.1
Дослідіть властивості дії на точку композиції двох симетрій відносно двох прямих, що перетинаються. Для дослідження сконструюйте ДР “Композиція двох симетрій відносно прямих”.
Завдання 86.1
Композиція рухів є рухом. Дослідіть рух, який є композицією двох поворотів.
Дослідіть рух, який є композицією двох поворотів, центри яких збігаються.
Дослідіть композицію двох поворотів з різними центрами.
Нижче наведено варіант ДР “Дослідження композиції поворотів”.
Зауваження
За допомогою комп’ютерних експериментів неважко здогадатися, що композиція двох поворотів у загальному випадку є також поворотом, і ці ж експерименти допоможуть визначати параметри результуючого повороту. Але як довести отриманий експериментально результат? Допомогти може дослідження композиції двох симетрій відносно прямих.
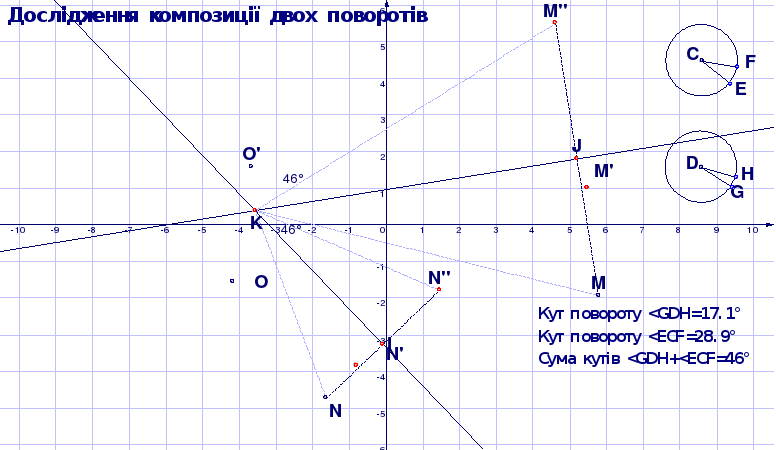
Рисунок 9.9 ДР "Дослідження властивостей композиції поворотів"
На рисунку 9.9 виконані побудови, для експериментальної перевірки того, що композиція поворотів є також поворот. Якщо це дійсно так, то центр повороту можна знайти за допомогою побудов, що наведено на рисунку — це буде точка перетину двох серединних перпендикулярів до пар точок “прообраз” – “образ” для композиції поворотів. Результати вимірювань показують, що дію композиції дійсно можна отримати в результаті повороту навколо знайденої точки. Більш за те, результати динамічних вимірювань показують, що величина цього повороту дорівнює алгебраїчній сумі двох поворотів, які утворюють композицію. Зрозуміло, що все це ми перевірили тільки для деякої кількості рисунків і перевірили з деякою заданою точністю, проте вірогідність справедливості цього факту у цілому, дуже велика (за особистим враженням можна сказати, що після комп’ютерного підтвердження гіпотези з’являється зовсім нове почуття впевненості у справедливості відповідної теореми і залишається тільки винахідницька задача — сконструювати, побудувати доведення, сумнівів немає, що воно існує).
Чи може допомогти комп’ютер на цьому етапі — етапі пошуку дедуктивного доведення? Зрозуміло, треба досліджувати конфігурацію, яку утворюють три точки — два центри вихідних поворотів та центр гіпотетичного повороту. Дослідимо трикутник, який вони утворюють — побудуємо сторони і виміряємо його кути та довжини сторін (результат наведено на наступному рисунку).
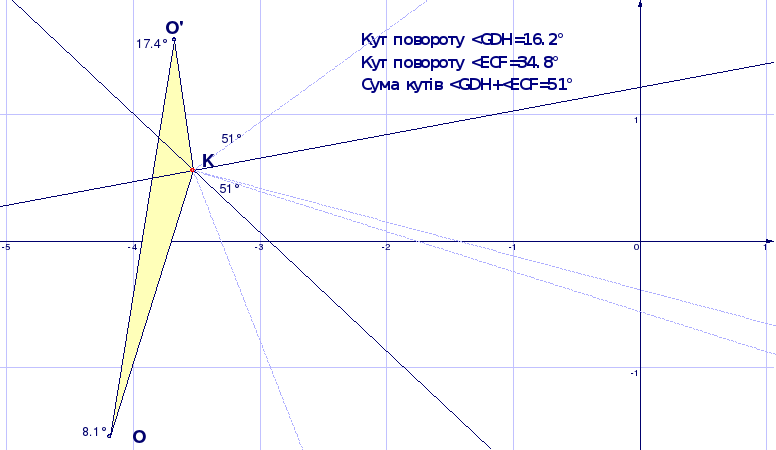
Рисунок 9.10 "Дослідження властивостей композиції поворотів"
“Еврика!” — два кути побудованого трикутника вдвічі менше за кути вихідних поворотів. Тепер нам буде у нагоді результат дослідження завдання 86.1, згідно якому композиція двох симетрій відносно прямих, що перетинаються є поворот відносно точки перетину на подвійний кут, що утворюють ці прямі (кут утворюється осями симетрії у напряму проти годинникової стрілки). Позначимо:
 — симетрія відносно прямої
— симетрія відносно прямої 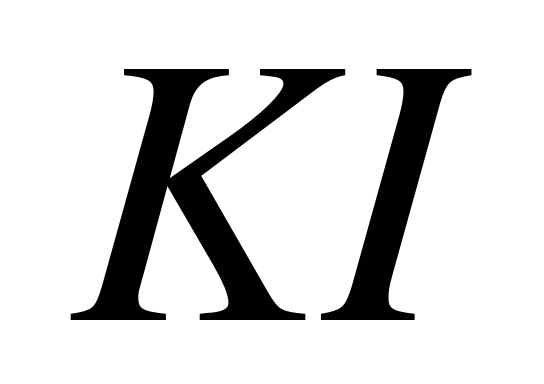 ;
; — симетрія відносно прямої
— симетрія відносно прямої  ;
;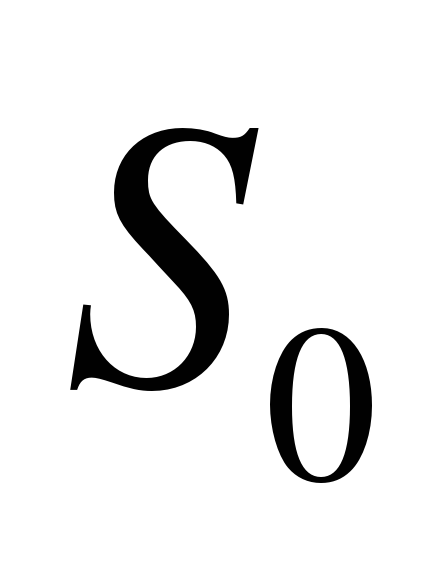 — симетрія відносно прямої
— симетрія відносно прямої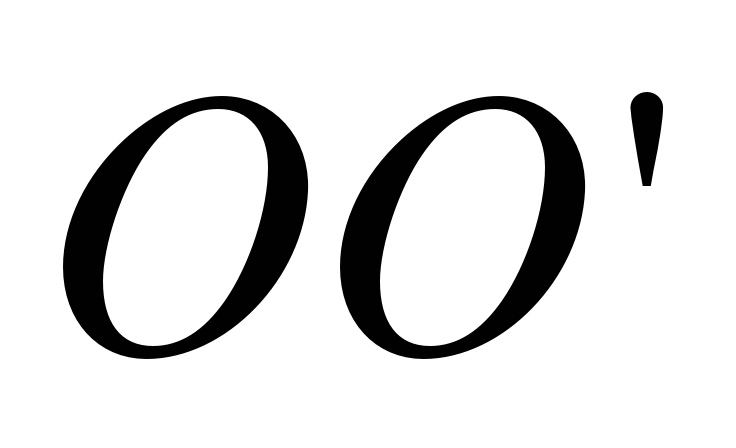 .
.
Згідно результатів дослідження завдання 86.1, перший поворот дорівнює композиції симетрій ![]() , другий — композиції
, другий — композиції ![]() , а композицію цих двох поворотів дорівнює (
, а композицію цих двох поворотів дорівнює (![]() )
)![]() . Виконуючи тотожні перетворення, отримаємо: (
. Виконуючи тотожні перетворення, отримаємо: (![]() )
)![]() =
=![]() 5. За результатом того ж дослідження (завдання 86.1), це і означає що композиція буде дорівнювати повороту навколо точки перетину прямих, що утворюють з лінією центрів повороту половинні кути, відкладені відповідно проти і за годинниковою стрілками на кут, що дорівнює алгебраїчній сумі вихідних кутів повороту.
5. За результатом того ж дослідження (завдання 86.1), це і означає що композиція буде дорівнювати повороту навколо точки перетину прямих, що утворюють з лінією центрів повороту половинні кути, відкладені відповідно проти і за годинниковою стрілками на кут, що дорівнює алгебраїчній сумі вихідних кутів повороту.
Таким чином, ми повністю розв’язали завдання 86.2 і дали два алгоритми побудови центра результуючого повороту. Комп’ютерні експерименти допомогли на усіх етапах дослідження — від формулювання гіпотези до її доведення.
Означення
Говорять, що геометрична фігура має поворотну симетрію порядку n, якщо вона суміщається з собою при повороті навколо деякої точки (яка називається центром симетрії цієї фігури) на кут 360/n. Наприклад, правильний трикутник має поворотну симетрію третього порядку відносно свого центру.
Для побудови та дослідження многокутників з поворотною симетрією n = 2, 3, 4, 5, 6, 7, 8 розробимо ДР “Поворотна симетрія”, зображення якого подано на рисунку.
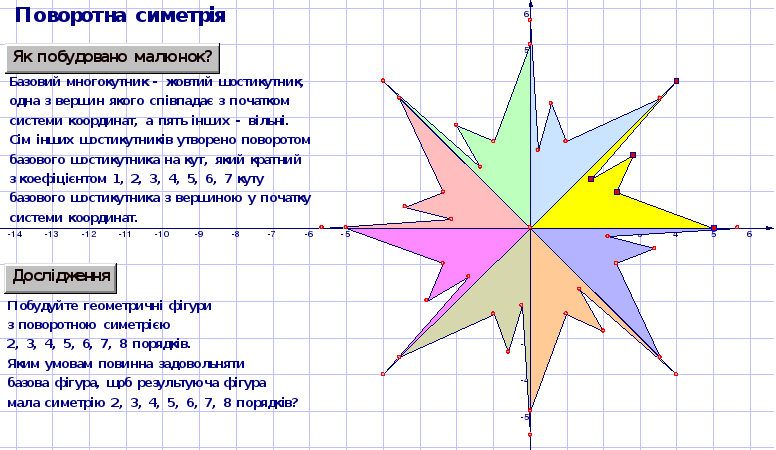
Рисунок 9.11 ДР “Поворотна симетрія”
Спочатку доцільно розробити макрос Rotate6Polygon, для повороту навколо будь-якої точки на будь-який кут будь-якого шестикутника.
Розробка макросу Rotate6Polygon
Побудуйте довільну точку — центр повороту;
Побудуйте довільні три точки, які будуть визначати величину кута повороту;
Побудуйте довільний шестикутник;
Побудуйте образи вершин шестикутника при повороті навколо центру на заданий кут, скориставшись макросом Rotate (для цього його треба спочатку макрос завантажити, скориставшись командою Макроси\Завантажити Макрос);
Побудуйте шестикутник з вершинами в образах вершин вихідного шестикутника (слід стежити за порядком вершин — він повинен відповідати порядку вершин вихідного шестикутника, інакше образ шестикутника не буде рівним вихідному шестикутника);
Відформуйте отриманий шестикутник згідно вашому смаку (наприклад, доцільно вилучити позначення вершин);
Виберіть команду Створити макрос з розділу головного меню Макроси і виконуйте дії згідно підказкам вікон діалогу:
Задайте вихідні параметри макросу (перша точка6 — центр кола, три точки — кут (у відповідності з заданням кута при геометричних побудовах));
Вкажіть результуючі параметри — многокутник;
Вкажіть ім’я макросу Rotate6Polygon (під таким ім’ям він буде фігурувати у списку завантажених макросів у розділі головного меню пакета Макроси);
Збережіть макрос на диску під ім’ям Rotate6Polygon.DGM
Протестуйте макрос, для чого почніть новий рисунок, вкажіть 10 точок (центр, кут, шестикутник) і виконайте макрос (вибрати в меню команду Макроси\Rotate6Polygon, вкажіть параметри макросу).
Побудова ДР “Поворотна симетрія”
Побудуйте кут із центром у початку системи координат, який дорівнює 45;
Побудуйте шестикутник (шестикутник вибрано тільки для того, щоб вистачало степенів свободи для побудови різноманітних шестикутників), одна з вершин якого розташовано у початку системи координат, дві суміжні на сторонах кута і три довільним чином розташовані в середині кута;
Побудуйте образ вихідного многокутника при повороті навколо початку системи координат на кут, який дорівнює вихідному кута, скориставшись макросом Rotate6Polygon;
Побудуйте образ многокутника, який було отримано на попередньому кроці, при повороті навколо початку системи координат на кут, який дорівнює вихідному кута, скориставшись макросом Rotate6Polygon;
Повторити попередній крок ще 6 разів, поки не буде отримано фігуру, яку утворюють вихідний многокутник і сім його образів при поворотах, які кратні базовому куту.
Розмаїття фігур, які можна побудувати за допомогою ДР “Поворотна симетрія” включає в себе правильні многокутники 2–8 порядків, різноманітні зірки 2–16 порядків. Це своєрідний електронний “поворотний калейдоскоп”, якого не можна створити оптичними пристроями, за аналогією із “симетричним калейдоскопом”, де симетрії відносно прямих реалізує система дзеркал. На рисунках наведено приклади фігур, які можна отримати за допомогою ДР “Поворотна симетрія”.
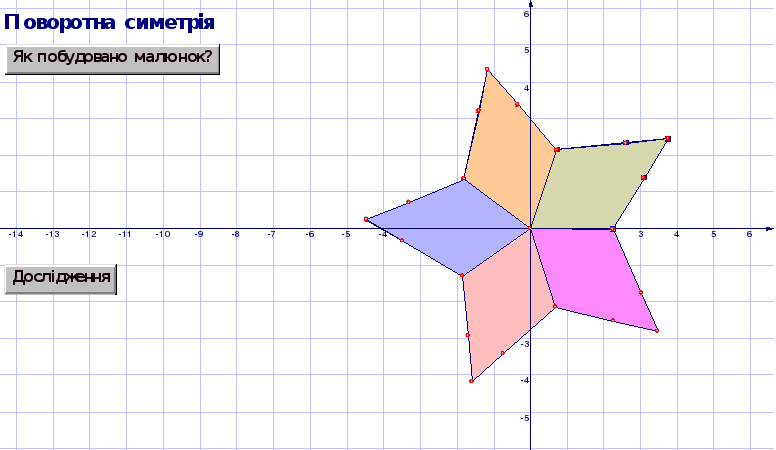
Рисунок 9.12 ДР “Приклад фігури з поворотною симетрією”.
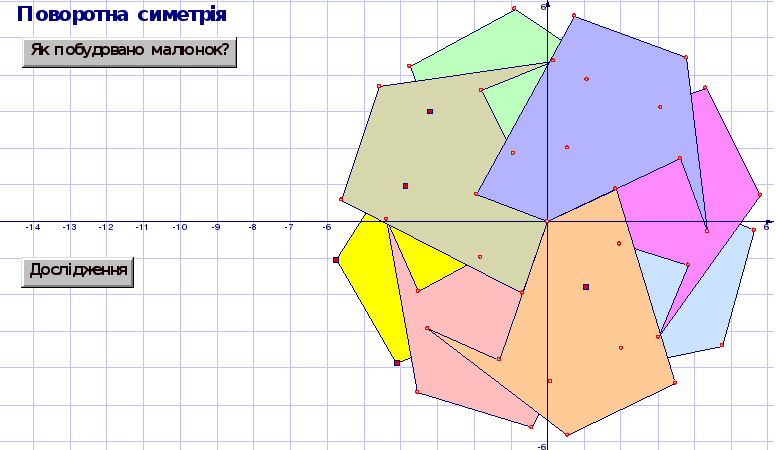
Рисунок 9.13 ДР "Магія поворотної симетрії"
Якщо вам сподобався “Поворотний калейдоскоп”, то по аналогії можете побудувати “Калейдоскоп симетрій” , в якому многокутник базового кута багатократно симетрично відбивається від прямої, що належить стороні кута.
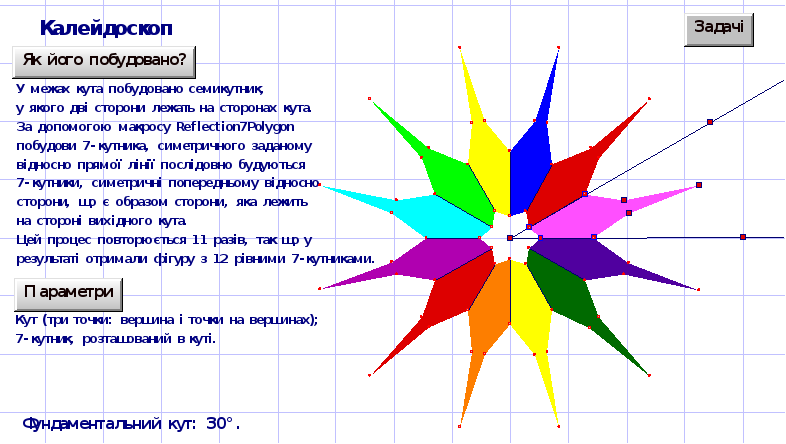
Рисунок 9.14 ДР "Калейдоскоп"
Побудова цього ДР аналогічна побудові ДР “Поворотна симетрія” і тому ми не будемо її детально обговорювати. Зауважимо тільки загальну схему побудови:
Розробити макрос Reflect7Angle побудови симетричного образу будь-якого семикутника відносно будь-якої прямої (за аналогією з розробкою макросу Rotate6Angle);
Побудувати кут за допомогою двох променів, які виходять із спільної точки;
Побудувати семикутник у границях кута, у якого дві сторони лежать на сторонах кута;
Побудувати семикутник, симетричний заданому відносно прямої лінії, на якій лежить сторона вихідного семикутника;
Послідовно побудувати семикутники, які симетричні семикутнику, який побудовано на попередньому кроці, повторюючи цей процес 11 разів, так що результуюча фігура утворюється 12 рівними 7-кутниками.
Завдання 9.86.2
Побудуйте правильний многокутник з 2, 3, .. 11, 12 сторонами.
Побудуйте правильну зірку з 2, 3, .. 11, 12 променями.
Побудуйте сніжинку, яка має 3 осі симетрії та поворотну симетрію 4 порядку.
Дослідіть, для яких m і n можна побувати сніжинку з m осями симетрії і поворотною симетрією порядку n.
Завдання 9.86.3
Сконструюйте електронну модель реального калейдоскопу.
1 Вперше це зробив видатний німецький математик Фелікс Клейн у своїй відомій Ерлангенській програмі (доповіді, яку він зробив, вступаючи на посаду професора Ерлангенського університету).
2 У 19 сторіччі вже нараховувалось багато геометрій: геометрія Евкліда, проективна геометрія, геометрія Лобачевского та інші).
3 З цього приводу можна порекомендувати познайомитись з чудовою книгою видатного німецького математика та філософа математики Германа Вейля “Симетрія”.
4 Нагадаємо, що функція Xangle(M, N) повертає величину кута між позитивним напрямом осі абсцис і вектором MN, який обчислюється проти годинникової стрілки і приймає значення в інтервалі [0, 360[.
5 Ми скористалися тим фактом, що композиція симетрії відносно прямої із нею самою є тотожне перетворення: ![]() (тобто перетворення, яке залишає на місці всі точки площини).
(тобто перетворення, яке залишає на місці всі точки площини).
6 Послідовність задання параметрів суттєва тільки з точки зору наступного коректного використання макросу —параметри макросу позиційні, тобто задаватися при виконанні вони повинні у тій же самій послідовності).
Просмотр содержимого документа
«10 Vectors»
Деякі фізичні величини характеризуються не тільки своїм числовим значенням, а й напрямом. Такі величини називаються векторними. Прикладом векторних величин є сила, швидкість, переміщення точки. Для спрощення роботи з векторними величинами користуються математичним поняттям вектора.
91. Абсолютна величина і напрям вектора
Вектором називають напрямлений відрізок. Для зображення вектора в пакеті DG можна скористатися командою Фігури\Аналітично\Вектор. Вказавши початок і кінець вектора, одержимо на екрані зображення вектора у вигляді стрілки. Вектор характеризується абсолютною величиною і напрямом. Нагадаємо, що абсолютною величиною (або модулем, або довжиною) вектора називається довжина відрізка, що зображає вектор.
Зі сказаного вище зрозуміло, що вектори знаходять широке використання у фізиці. Але в багатьох випадках і при побудові математичних теорій зручно використовувати вектори. З прикладами застосування векторів при розв’язуванні геометричних задач ви познайомитеся при вивченні курсу геометрії.
Щ
об проілюструвати поняття абсолютної величини і напряму вектора, покажемо як можна використати вектори для задання кривих. Для цього розробимо ДР “Вектор малює криву” (рис. 91.1). Відобразимо на екрані осі декартової системи координат. Побудуємо зображення вектора ![]() . Початок вектора — точка O — збігається з початком системи координат, а кінець вектора — точка M — має такі координати:
. Початок вектора — точка O — збігається з початком системи координат, а кінець вектора — точка M — має такі координати: ![]() , де параметр t належить відрізку [–2; 2]. Спочатку побудуємо відрізок з кінцями в точках A(–2; 0) і B(2; 0). Для цього виберемо інструмент Точка фігури і клацнемо мишею в двох точках осі абсцис. Одержимо дві напівзалежні точки A і B. Перемістимо їх вздовж осі абсцис в потрібне положення і з’єднаємо відрізком. Побудуємо довільну точку t відрізка AB. Абсциса точки t буде задавати значення параметра t, від якого залежать координати точки M. Для побудови точки M скористаємося командою Фігури\Аналітично\Точка. В текстових полях Х= і Y= діалогового вікна задамо координати точки M: ((t.X)^2)/((t.X)^2 + 1) і (t.X) * (1 – (t.X) ^2)) / ((t.X) ^ 2 + 1). Побудуємо тепер вектор з початком у точці O(0; 0) і кінцем у точці M.
, де параметр t належить відрізку [–2; 2]. Спочатку побудуємо відрізок з кінцями в точках A(–2; 0) і B(2; 0). Для цього виберемо інструмент Точка фігури і клацнемо мишею в двох точках осі абсцис. Одержимо дві напівзалежні точки A і B. Перемістимо їх вздовж осі абсцис в потрібне положення і з’єднаємо відрізком. Побудуємо довільну точку t відрізка AB. Абсциса точки t буде задавати значення параметра t, від якого залежать координати точки M. Для побудови точки M скористаємося командою Фігури\Аналітично\Точка. В текстових полях Х= і Y= діалогового вікна задамо координати точки M: ((t.X)^2)/((t.X)^2 + 1) і (t.X) * (1 – (t.X) ^2)) / ((t.X) ^ 2 + 1). Побудуємо тепер вектор з початком у точці O(0; 0) і кінцем у точці M.
Нехай тепер точка t пробігає відрізок AB. Тоді кінець вектора ![]() опише деяку криву. Для її побудови скористаємося командою Фігури\Побудови\Динамічний слід.
опише деяку криву. Для її побудови скористаємося командою Фігури\Побудови\Динамічний слід.
З наукової точки зору
Кожному числу t з деякого відрізка [a; b] ми поставили у відповідність вектор ![]() , який залежить від t. В цьому випадку кажуть, що на відрізку [a; b] задана вектор-функція
, який залежить від t. В цьому випадку кажуть, що на відрізку [a; b] задана вектор-функція ![]() . Якщо вектори
. Якщо вектори ![]() відкладені від однієї точки, то їх кінці описують деяку криву, яка називається годографом вектор-функції
відкладені від однієї точки, то їх кінці описують деяку криву, яка називається годографом вектор-функції ![]() . Будь-яку криву можна розглядати як годограф деякої вектор-функції.
. Будь-яку криву можна розглядати як годограф деякої вектор-функції.
Завдання 91.1
Використовуючи ДР “Вектор малює криву”, побудуйте криву, яку описують кінці векторів ![]() , якщо точки М мають координати (t; t2), t[–3; 3].
, якщо точки М мають координати (t; t2), t[–3; 3].
92. Рівність векторів
Вектори ![]() і
і ![]() називаються рівними, якщо вони суміщаються паралельним перенесенням, тобто існує паралельне перенесення, яке переводить точку A в точку C, а точку B — в точку D. Відмітимо таку властивість паралелограма: якщо чотирикутник ABCD — паралелограм, то вектори
називаються рівними, якщо вони суміщаються паралельним перенесенням, тобто існує паралельне перенесення, яке переводить точку A в точку C, а точку B — в точку D. Відмітимо таку властивість паралелограма: якщо чотирикутник ABCD — паралелограм, то вектори ![]() і
і ![]() рівні (задача 2, §10). Цю властивість можна використати для побудови шарнірного механізму, що реалізує паралельне перенесення. Під шарнірним механізмом ми розуміємо зв’язний набір стержнів, кінці яких частково з’єднані між собою шарнірами так, що конструкція зберігає рухомість. Звичайно ми будемо будувати комп’ютерну модель шарнірного механізму. Шарнірний механізм для побудови образа фігури при паралельному перенесенні складається з двох паралелограмів ABDC і CDFE (рис. 92.1). Паралелограм (на відміну від трикутника) не є жорсткою фігурою: якщо сусідні сторони паралелограма з’єднати шарнірами у вершинах, то він зберігає рухомість. Сторони АС і EC паралелограмів дорівнюють відрізку PQ. Переміщуючи точки A і B, задамо напрям і величину паралельного перенесення. Якщо тепер точка E опише деяку фігуру F1, то залежна точка F побудує фігуру F2 — образ фігури F1 при паралельному перенесенні на вектор AB. Дійсно, при будь-якому положенні точки E вектор
рівні (задача 2, §10). Цю властивість можна використати для побудови шарнірного механізму, що реалізує паралельне перенесення. Під шарнірним механізмом ми розуміємо зв’язний набір стержнів, кінці яких частково з’єднані між собою шарнірами так, що конструкція зберігає рухомість. Звичайно ми будемо будувати комп’ютерну модель шарнірного механізму. Шарнірний механізм для побудови образа фігури при паралельному перенесенні складається з двох паралелограмів ABDC і CDFE (рис. 92.1). Паралелограм (на відміну від трикутника) не є жорсткою фігурою: якщо сусідні сторони паралелограма з’єднати шарнірами у вершинах, то він зберігає рухомість. Сторони АС і EC паралелограмів дорівнюють відрізку PQ. Переміщуючи точки A і B, задамо напрям і величину паралельного перенесення. Якщо тепер точка E опише деяку фігуру F1, то залежна точка F побудує фігуру F2 — образ фігури F1 при паралельному перенесенні на вектор AB. Дійсно, при будь-якому положенні точки E вектор ![]() дорівнює вектору
дорівнює вектору ![]() (чому?).
(чому?).
Завдання 92.1
Побудуйте фізичну модель шарнірного механізму для реалізації паралельного перенесення. 
93. Координати вектора
Розробимо ДР “Координати вектора”. Побудуємо вектор ![]() з початком у довільній точці A. Координати вектора будемо задавати, переміщуючи точки х і y вздовж координатних осей: координата x буде дорівнювати абсцисі точки х, а координата y — ординаті точки y. Побудови виконаємо у такій послідовності:
з початком у довільній точці A. Координати вектора будемо задавати, переміщуючи точки х і y вздовж координатних осей: координата x буде дорівнювати абсцисі точки х, а координата y — ординаті точки y. Побудови виконаємо у такій послідовності:
Відобразимо на екрані осі координат і побудуємо точки х і y на осях абсцис і ординат відповідно.
Побудуємо довільну точку A.
Побудуємо точку В за її координатами: А.Х + х.Х і А.Y + y.Y (Побудови\Аналітично\Точка).
Побудуємо вектор АВ (Побудови\Аналітично\Вектор).
Паралельним перенесенням фігури F на вектор ![]() називається перетворення фігури F, при якому довільна її точка M переходить у точку M таку, що
називається перетворення фігури F, при якому довільна її точка M переходить у точку M таку, що ![]() . Якщо вектор
. Якщо вектор ![]() має координати a і b, то паралельне перенесення на вектор
має координати a і b, то паралельне перенесення на вектор ![]() задається формулами: x x + a, y y b, тобто довільна точка (x; y) переходить у точку (x + a; y b), де a і b одні й ті самі для всіх точок (x; y). Отже, паралельне перенесення фігури F на вектор
задається формулами: x x + a, y y b, тобто довільна точка (x; y) переходить у точку (x + a; y b), де a і b одні й ті самі для всіх точок (x; y). Отже, паралельне перенесення фігури F на вектор ![]() дійсно є паралельним перенесенням.
дійсно є паралельним перенесенням.
Використовуючи ДР “Координати вектора”, побудуємо образ кола при паралельному перенесенні на вектор ![]() . Спочатку побудуємо коло з центром O, яке проходить через точку D. Пристебнемо початок вектора — точку A — до кола. Для цього перемістимо точку A до однієї із точок кола і клацнемо на точці A правою точкою миші. В контекстному меню виберемо команду Пристебнути. Якщо тепер переміщувати точку A вздовж кола, то кінець вектора
. Спочатку побудуємо коло з центром O, яке проходить через точку D. Пристебнемо початок вектора — точку A — до кола. Для цього перемістимо точку A до однієї із точок кола і клацнемо на точці A правою точкою миші. В контекстному меню виберемо команду Пристебнути. Якщо тепер переміщувати точку A вздовж кола, то кінець вектора ![]() опише коло, в яке перейде дане коло при паралельному перенесенні на вектор
опише коло, в яке перейде дане коло при паралельному перенесенні на вектор ![]() . Для його побудови скористаємося командою Фігури\Побудови\Динамічний слід. Обравши зазначену команду, клацнемо мишею спочатку на точці B, а потім на точці A. Побудований слід точки B є динамічним. Це означає, що він буде будуватися заново при зміні початкових об’єктів нашого рисунка.
. Для його побудови скористаємося командою Фігури\Побудови\Динамічний слід. Обравши зазначену команду, клацнемо мишею спочатку на точці B, а потім на точці A. Побудований слід точки B є динамічним. Це означає, що він буде будуватися заново при зміні початкових об’єктів нашого рисунка.
9
4. Додавання векторів
Завдання 94.1
Т очки A, B і C — вершини трикутника. Вектор
очки A, B і C — вершини трикутника. Вектор ![]() — сума векторів
— сума векторів ![]() ,
, ![]() і
і ![]() (рис. 94.1). Дослідіть за допомогою ДР “Сума векторів”, при якому положенні точки O вектор
(рис. 94.1). Дослідіть за допомогою ДР “Сума векторів”, при якому положенні точки O вектор ![]() нульовий. Доведіть, що існує тільки одна точка O така, що
нульовий. Доведіть, що існує тільки одна точка O така, що ![]() .
.
Розгляньте аналогічну задачу для чотирьох точок: в площині чотирикутника ABCD знайдіть таку точку O, щоб сума векторів ![]() дорівнювала нулю. Розробіть динамічний рисунок для розв’язування задачі в пакеті DG. Виконайте експерименти, сформулюйте гіпотезу, перевірте її, використовуючи динамічні властивості пакету, і у випадку підтвердження знайдіть дедуктивне доведення.
дорівнювала нулю. Розробіть динамічний рисунок для розв’язування задачі в пакеті DG. Виконайте експерименти, сформулюйте гіпотезу, перевірте її, використовуючи динамічні властивості пакету, і у випадку підтвердження знайдіть дедуктивне доведення.
Доведіть, що для довільних точок A1, A2, … , An існує, причому тільки одна, точка O така, що ![]() .
.
Однією з векторних величин, що вивчаються у фізиці, є швидкість. Чи є та чи інша величина векторною, встановлюється дослідним шляхом. Фізичні експерименти показують, що швидкості додаються за векторним законом. Векторне додавання швидкостей можна продемонструвати на прикладі парому, що переміщується від одного берега річки до іншого.
З
авдання 94.2
Дано швидкість vп парому в стоячій воді і швидкість vр течії річки. Використовуючи ДР “Додавання швидкостей” (рис.94.2), знайдіть кут під яким повинен тримати курс паром, щоб він рухався перпендикулярно берегу річки, якщо:
vп = 6 км/год, vр = 3 км/год;
2) vп = 3 км/год, vр = 2 км/год.
95. Додавання сил
Завдання 95.1
На похилій площині з кутом нахилу розміщено вантаж вагою P. Використовуючи ДР “Вантаж на похилій площині” (рис. 95.1) знайдіть силу, з якою треба утримувати вантаж, щоб він не скочувався вниз, якщо:
= 30, P = 3 Н;
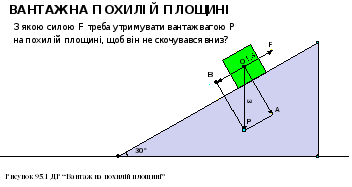
= 30, P = 6 Н; = 45, P = 4,7 Н.
96. Множення вектора на число
Добутком вектора ![]() на число k називається вектор
на число k називається вектор ![]() . Розглянемо побудову ДР “Множення вектора на число” (рис. 96.1). На рисунку
. Розглянемо побудову ДР “Множення вектора на число” (рис. 96.1). На рисунку ![]() . Число k дорівнює абсцисі точки k, яка лежить на осі 0х. Побудову виконаємо у такій послідовності:
. Число k дорівнює абсцисі точки k, яка лежить на осі 0х. Побудову виконаємо у такій послідовності:
Будуємо довільний вектор
 (Фігури\Аналітично\Вектор).
(Фігури\Аналітично\Вектор).Будуємо довільну точку k на осі абсцис (інструмент Точка фігури).
Будуємо точку C. Для цього скористаємося командою Фігури\Аналітично\Точка. В діалоговому вікні, що з’явиться задамо координати точки C: A.X + k.X*(B.X – A.X) і A.Y + k.X*(B.Y – A.Y) .
Будуємо вектор
 .
.
Завдання 96.1
Н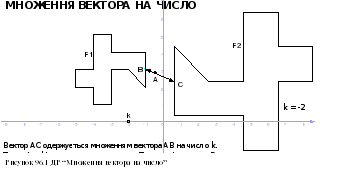
ехай кінець вектора ![]() описує відрізок. Переконайтесь і доведіть, що кінець вектора
описує відрізок. Переконайтесь і доведіть, що кінець вектора ![]() також описує відрізок. Дослідіть, як зв’язані довжини цих відрізків.
також описує відрізок. Дослідіть, як зв’язані довжини цих відрізків.
97. Розкладання вектора за двома неколінеарними векторами
Будь-який вектор можна розкласти за двома неколінеарними векторами: якщо вектори ![]() і
і ![]() неколінеарні, то будь-який вектор
неколінеарні, то будь-який вектор ![]() можна записати у вигляді
можна записати у вигляді ![]() . Розробимо в пакеті DG динамічний рисунок для розв’язування цієї задачі. Нехай
. Розробимо в пакеті DG динамічний рисунок для розв’язування цієї задачі. Нехай ![]() і — неколінеарні вектори. Розкладемо довільний вектор за векторами
і — неколінеарні вектори. Розкладемо довільний вектор за векторами ![]() і . Через точки A і B проведемо прямі, паралельні векторам
і . Через точки A і B проведемо прямі, паралельні векторам ![]() і . Позначимо через A1 і B1 точки перетину цих прямих з прямими OA і OB відповідно. За правилом паралелограма . Оскільки вектор колінеарний ненульовому вектору
і . Позначимо через A1 і B1 точки перетину цих прямих з прямими OA і OB відповідно. За правилом паралелограма . Оскільки вектор колінеарний ненульовому вектору ![]() , то . Аналогічно . Отже, . Зазначимо, що , причому 0, якщо вектори
, то . Аналогічно . Отже, . Зазначимо, що , причому 0, якщо вектори ![]() і однаково напрямлені, і і протилежно напрямлені. Аналогічно , причому 0, якщо вектори і однаково напрямлені, і і протилежно напрямлені.
і однаково напрямлені, і і протилежно напрямлені. Аналогічно , причому 0, якщо вектори і однаково напрямлені, і і протилежно напрямлені.
Алгоритм побудови динамічного рисунка тепер зрозумілий (рис.97.1). При створенні динамічного надпису скористаємося умовною функцією IF(Умова, Вираз1, Вираз2). Першим аргументом функції IF є логічний вираз. Якщо він приймає значення True (тобто, Умова виконується), то функція IF повертає Вираз1. Якщо ж перший аргумент приймає значення False (тобто, Умова не виконується), то функція IF повертає Вираз2. В текстовому полі діалогового вікна Властивості надпису напишемо вираз:
OС = ([If((A1.X – O.X)*(A.X – O.X) 0, 1, –1)*Dist(O, A1)/Dist(O, A)])*OA + ([If((B1.X – O.X)*(B.X – O.X) 0, 1, –1)*Dist(O, B1)/Dist(O, B)])*OB
Завдання 97.1
Використовуючи ДР “Розкладання вектора за двома неколінеарними векторами” (рис. 97.1), розкладіть вектор за векторами ![]() і
і ![]() , якщо:
, якщо:
, , ;
, , ;, , .
98. Скалярний добуток векторів
Скалярним добутком векторів і називається число . У підручнику доведено, що скалярний добуток векторів не залежить від вибору системи координат. Крім того показано, що скалярний добуток векторів дорівнює добутку їх абсолютних величин на косинус кута між ними. Зауважимо, що скалярний добуток векторів використовується у фізиці для знаходження роботи сили. Якщо вектор зображує силу, точка прикладення якої переміщується із початку в кінець вектора , то робота w цієї сили дорівнює скалярному добутку векторів і : w = .
З
авдання 98.1
Використовуючи ДР “Робота сили" (рис. 98.1), дослідіть, чому дорівнює робота сили, точка прикладання якої перемістилася із точки A в ту ж саму точку A по замкненій ламаній. Доведіть твердження, отримане в результаті експериментів в пакеті DG.
Просмотр содержимого документа
«11 Similarity»
100. Перетворення подібності
В § 9 ми вивчали рухи — перетворення фігури F у фігуру F`, при яких зберігаються відстані між точками. Як ми бачили, фігура F`, в яку при русі переходила фігура F, не відрізнялась від фігури F ні формою, ні розмірами. Тепер ми розглянемо більш широкий клас геометричних перетворень — перетворення подібності. Нагадаємо, що перетворення фігури F у фігуру F` називається перетворенням подібності з коефіцієнтом k (k 0), якщо при цьому перетворенні відстані між точками змінюються в k разів: для довільних точок X і Y фігури F та їх образів X` і Y`(тобто, точок X` і Y` фігури F`, у які перейшли точки X і Y) виконується рівність X`Y` = k .XY.
Д
ля експериментального дослідження властивостей перетворення подібності можна скористатися ДР “Перетворення подібності” (Рис. 100.1). На динамічному рисунку точка X` — образ точки X при перетворені подібності. Змінюючи положення точок k, t, x0, y0, e можна задавати параметри перетворення подібності.
Завдання 100.1
1. Побудуйте довільний відрізок PQ. Побудуйте динамічний образ відрізка PQ при перетворенні подібності. Змінюйте положення точок P і Q та параметри перетворення подібності. Які гіпотези можна висунути із ваших спостережень.
2. Дослідіть експериментально дію перетворення подібності на коло.
3. Побудуйте образ довільної фігури при перетворенні подібності. Для цього виберіть в контекстному меню точок X і X` команду “Залишити слід”. Переміщуючи точку X за допомогою миші, намалюйте довільну фігуру F. При цьому точка X` опише деяку фігуру F`. Порівняйте фігури F і F`. Яку спільну властивість вони мають?
Важливим прикладом перетворення подібності є гомотетія. При перетворенні гомотетії з центром O і коефіцієнтом k довільна точка X фігури F переходить в точку X` фігури F` таку, що ![]() .
.
Для побудови точки X`, гомотетичної точці Х, можна скористатися ДР “Множення вектора на число”, який ми використовували при вивченні лінійних операцій над векторами.
Завдання 100.2
1. Використовуючи ДР “Множення вектора на число”, перевірте експериментально, що гомотетія є перетворенням подібності.
2. Доведіть, що гомотетія з коефіцієнтом k є перетворенням подібності з коефіцієнтом | k |. (Зауважимо, що гомотетію можна розглядати і з від’ємним коефіцієнтом).
Behind the Scenes
При розробці ДР “Перетворення подібності”, ми скористалися координатними формулами перетворення подібності. Можна довести, що будь-яке перетворення подібності з коефіцієнтом k є результатом гомотетії з тим же коефіцієнтом та центром у довільній точці та деякого руху площини. Якщо при гомотетії з центром у початку координат точка (x; y) перейшла у точку ![]() , то
, то
![]()
Нехай тепер при русі точка ![]() переходить у точку (x`; y`). У курсі аналітичної геометрії доводиться, що рух площини можна задати формулами
переходить у точку (x`; y`). У курсі аналітичної геометрії доводиться, що рух площини можна задати формулами
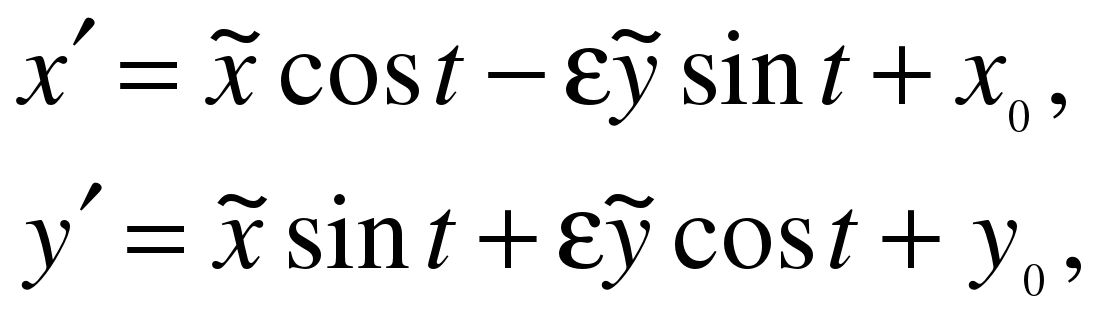
де 1 або –1.
Отже, якщо при перетворенні подібності довільна точка (x; y) переходить у точку (x`; y`) , то
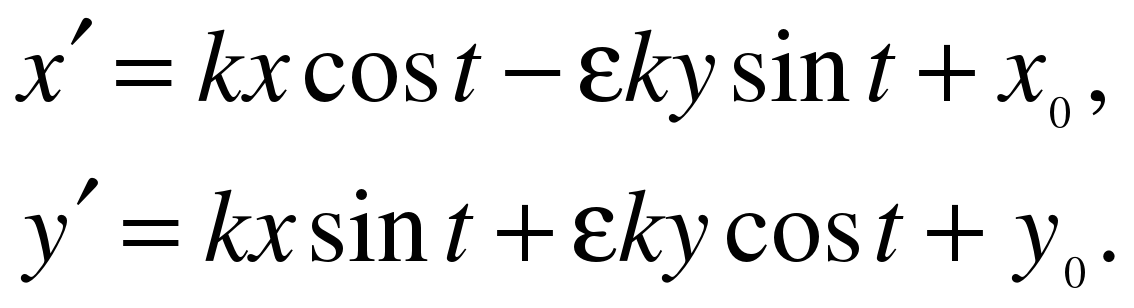 (*)
(*)
Формули (*) і були використані при побудові динамічного рисунку.
101. Властивості перетворення подібності
Завдання 101.1
Використовуючи ДР “Перетворення подібності”, переконайтеся, що перетворення подібності зберігає кути між півпрямими.
102. Подібність фігур
Завдання 102.1
Використовуючи ДР “Подібність трикутників” (Рис. 102.1), переконайтеся, що у подібних трикутників ABC і PQR відповідні кути рівні, а відповідні сторони пропорційні:
A = P, B = Q, C = R;

![]()
103. Ознака подібності трикутників за двома кутами
Нагадаємо, що два трикутники називаються подібними, якщо вони переводяться один в один перетворенням подібності. Користуватися означенням для доведення подібності трикутників не завжди зручно: для доведення подібності трикутників потрібно переконатися, що існує перетворення подібності, яке один трикутник відображає на інший. Простіше скористатися ознаками подібності трикутників.
Завдання 103.1
Д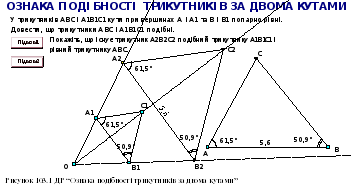
оведіть ознаку подібності трикутників за двома кутами: якщо два кути одного трикутика відповідно дорівнюють двом кутам другого трикутника, то такі трикутники подібні (Рис. 103.1).
104. Ознака подібності трикутників за двома сторонами і кутом між ними
Завдання 104.1
Д
оведіть ознаку подібності трикутників за двома сторонами і кутом між ними: якщо дві сторони одного трикутника пропорційні двом сторонам другого трикутника і кути, утворені цими сторонами, рівні, то такі трикутники подібні (Рис. 104.1).
105. Ознака подібності трикутників за трьома сторонами
Завдання 105.1
Д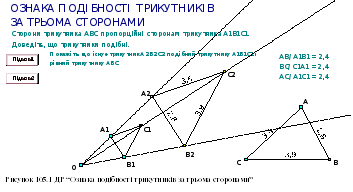
оведіть ознаку подібності трикутників за трьома сторонами: якщо сторони одного трикутника пропорційні сторонам другого трикутника, то такі трикутники подібні (Рис. 105.1)
106. Подібність прямокутних трикутників

Завдання 106.1
Доведіть, що висота h ліхтаря над поверхнею Землі не залежить від відстані між стовпами (Рис. 106.1).
107. Кути, вписані в коло
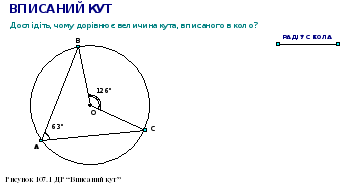
Завдання 107.1
За допомогою динамічних експериментів у пакеті DG дослідіть, чому дорівнює величина кута, вписаного в коло (Рис. 107.1).
Побудуйте геометричне місце вершин кутів з даною градусною мірою, сторони яких проходять через кінці даного відрізка. Створіть в пакті DG макрос для побудови зазначеного геометричного місця точок.
Дано два відрізки a і b. Побудуйте точку, із якої відрізок a видно під кутом 30, а відрізок b — під кутом 150. Задайте таке положення відрізків a і b, щоб задача мала:
7 розв’язків;
8 розв’язків.
Чи може задача мати 9 розв’язків?
108. Пропорційність відрізків хорд і січних кола
Завдання 108.1
На прямій MN знайти точку Х, для якої довжини відрізків дотичних, проведених до двох кіл, що перетинаються, були б рівними (Рис. 108.1).
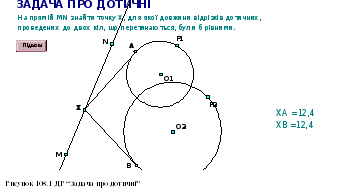
Похожие файлы
object(ArrayObject)#865 (1) {
["storage":"ArrayObject":private] => array(6) {
["title"] => string(75) "Конспект урока Сумма углов треугольника "
["seo_title"] => string(43) "konspiekt-uroka-summa-ughlov-trieughol-nika"
["file_id"] => string(6) "175519"
["category_seo"] => string(10) "matematika"
["subcategory_seo"] => string(5) "uroki"
["date"] => string(10) "1424275134"
}
}
object(ArrayObject)#887 (1) {
["storage":"ArrayObject":private] => array(6) {
["title"] => string(75) "Открытый урок "сумма углов треугольника" "
["seo_title"] => string(41) "otkrytyi-urok-summa-ughlov-trieughol-nika"
["file_id"] => string(6) "201266"
["category_seo"] => string(10) "matematika"
["subcategory_seo"] => string(5) "uroki"
["date"] => string(10) "1429017370"
}
}
object(ArrayObject)#865 (1) {
["storage":"ArrayObject":private] => array(6) {
["title"] => string(283) "Конспект урока геометрии 9 кл. "Правильный многоугольник. Сумма углов выпуклого многоугольника" по методике изучения уровня обучаемости по Третьякову П.И."
["seo_title"] => string(80) "konspiekt_uroka_ghieomietrii_9_kl_pravil_nyi_mnoghoughol_nik_summa_ughlov_vypukl"
["file_id"] => string(6) "375058"
["category_seo"] => string(10) "matematika"
["subcategory_seo"] => string(5) "uroki"
["date"] => string(10) "1483443229"
}
}
object(ArrayObject)#887 (1) {
["storage":"ArrayObject":private] => array(6) {
["title"] => string(105) "Конспект и презентация урока "Правильные многоугольники""
["seo_title"] => string(62) "konspiekt_i_priezientatsiia_uroka_pravil_nyie_mnoghoughol_niki"
["file_id"] => string(6) "378198"
["category_seo"] => string(10) "matematika"
["subcategory_seo"] => string(11) "presentacii"
["date"] => string(10) "1484157054"
}
}
object(ArrayObject)#865 (1) {
["storage":"ArrayObject":private] => array(6) {
["title"] => string(80) "Конспект урока "Правильные многоугольники" "
["seo_title"] => string(44) "konspiekt-uroka-pravil-nyie-mnoghoughol-niki"
["file_id"] => string(6) "176224"
["category_seo"] => string(10) "matematika"
["subcategory_seo"] => string(5) "uroki"
["date"] => string(10) "1424370974"
}
}
Подтверждение авторства
Пожалуйста, введите ваш Email.
Если вы хотите увидеть все свои работы, то вам необходимо войти или зарегистрироваться
Полезное для учителя
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
















