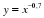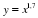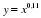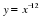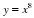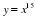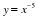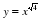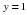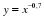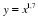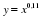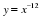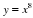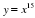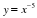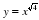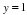Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Степенная функция, её свойства и график
Конспект урока по математике по теме «Степенная функция, её свойства и график»
Преподаватель математики ГБПОУ МО «СТТ»
Голубева Наталья Борисовна
Дата урока
Тема урока Степенная функция, её свойства и график
Цель урока 1. Формирование опорной системы знаний по теме «Степенная функция, её свойства и график»
2. Первичное осознание нового учебного материала
Задачи урока
Образовательные
Повторить и обобщить знания обучающихся по теме «Степенная функция», изученные в 9 классе.
Развивающие
Развивать творческую и мыслительную деятельность учащихся, их интеллектуальные качества: способность к «видению» проблемы.
Формировать умения чётко и ясно излагать свои мысли.
Развивать пространственное воображение учащихся.
Воспитательные
Воспитывать умение работать с имеющейся информацией в необычной ситуации.
Компетенции
Формирование языковой, коммуникативной и информационных общих компетенций.
ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения задач.
ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.
ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения задач.
ОК 5. Использовать информационно-коммуникационные технологии.
ОК 6. Работать в коллективе и команде, эффективно общаться с учителем, товарищами.
ОК 7. Брать на себя ответственность за работу членов команды (подчиненных), результат выполнения заданий.
ОК 8. Самостоятельно определять задачи личностного развития, заниматься самообразованием.
Тип урока Урок усвоения новых знаний
Форма урока комбинированный урок
Педагогическая технология Элементы информационно-коммуникационной, игровой
Метод урока объяснительно-иллюстративный, репродуктивный.
Средства обучения
Компьютер, мультимедийный проектор, ноутбуки для проведения тестирования.
Приложение 1, презентация Microsoft PowerPoint.
«Опорный конспект». Приложение 3, документ Microsoft Word.
тест, созданный с помощью программы My TestX представленной на сайте www.klyaksa.net . Программа MyTestX распространяется бесплатно.
Раздаточный материал для повторения. Приложение 2, документ Microsoft Word.
Карточки с номерами эскизов. Приложение 4, документ Microsoft Word.
Структура урока
1. Организационный этап (1 мин)
Заполнение журнала, отметка присутствующих на уроке, проверка готовности учащихся к уроку.
Ход урока
2. Этап подготовки к активному сознательному усвоению знаний 5 мин
Повторение основных понятий.
1. Область определения.
(значения, которые может принимать переменная х.)
2. Область значений (множество значений).
(множество значений, которые может принимать переменная у.)
3. Четность, нечетность функции.
Графическая иллюстрация четной, нечетной функции.
(график четной функции симметричен относительно оси ОУ.
график нечетной функции симметричен относительно начала координат, т.е точки О)
Аналитическая запись свойства четности, нечетности.
(y(-x)=-y(x) - нечетная функция
y(-x)=y(x) - четная функция)
4. Промежутки возрастания и убывания функции.
3. Этап усвоения новых знаний 14 мин
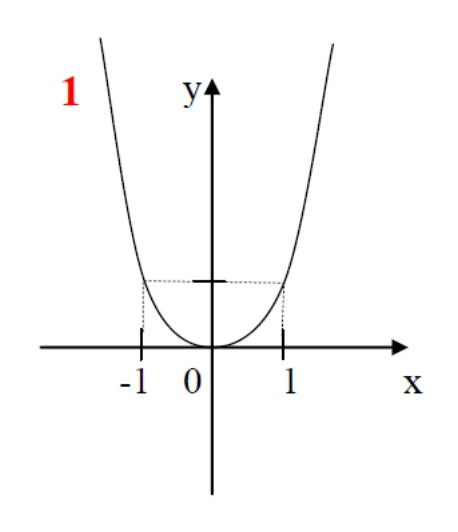
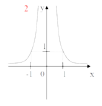
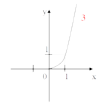
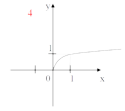
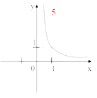
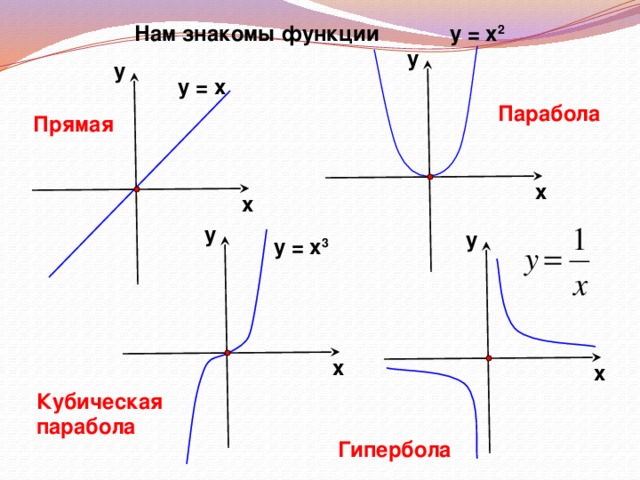
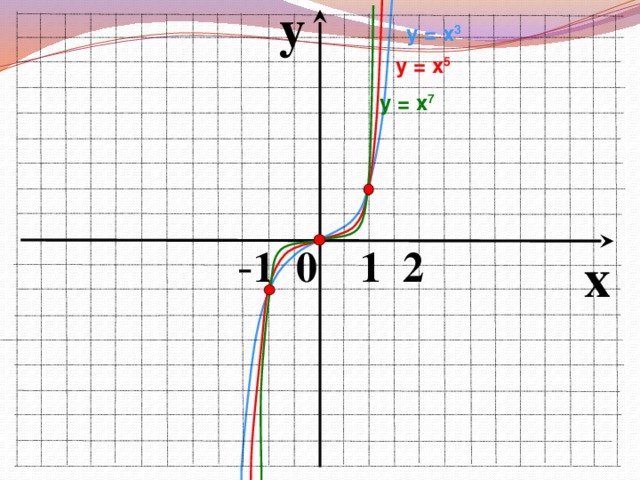
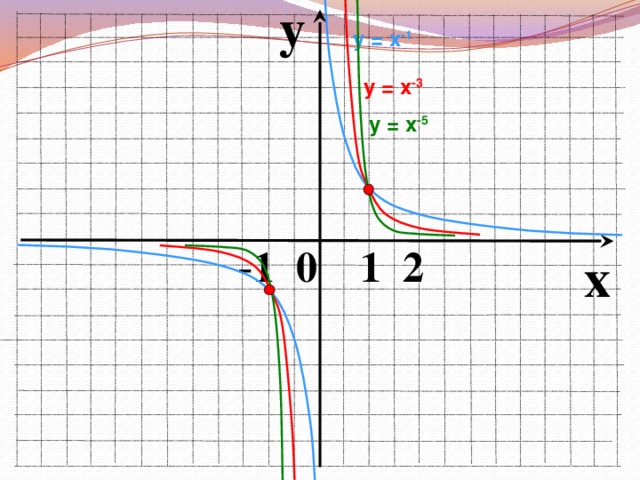
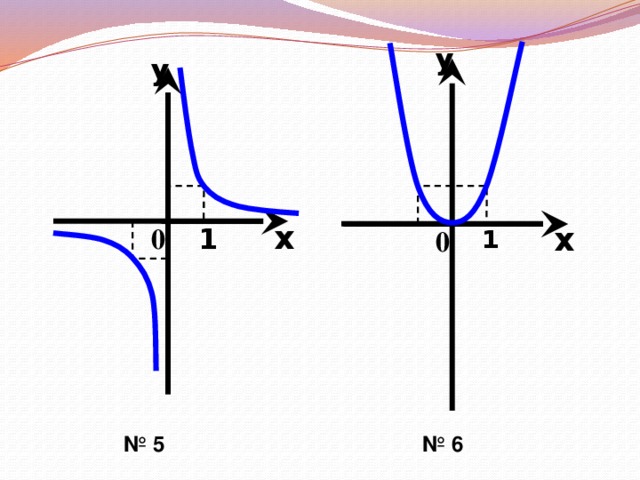
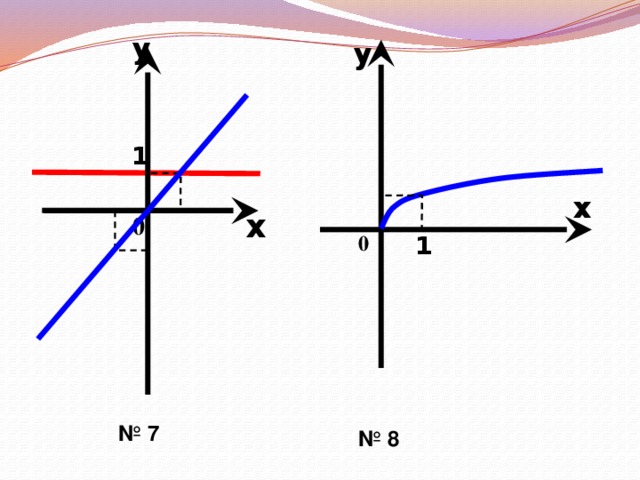
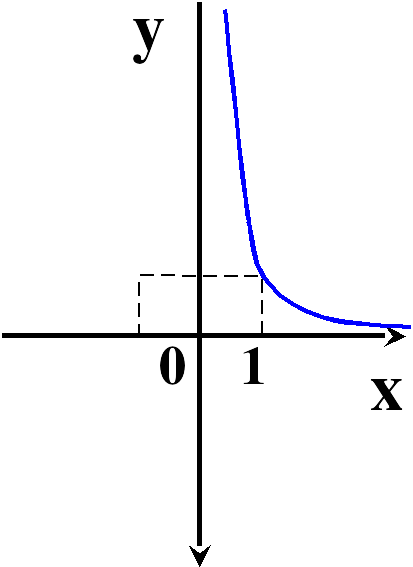
Сегодня на уроке мы повторим и систематизируем наши знания по теме «Степенная функция». Слайд 3. С седьмого класса мы изучили множество функций, графики которых вы видите на слайде.
Что объединяет все эти функции?
Все эти функции являются частными случаями степенной функции.
Дадим определение степенной функции.
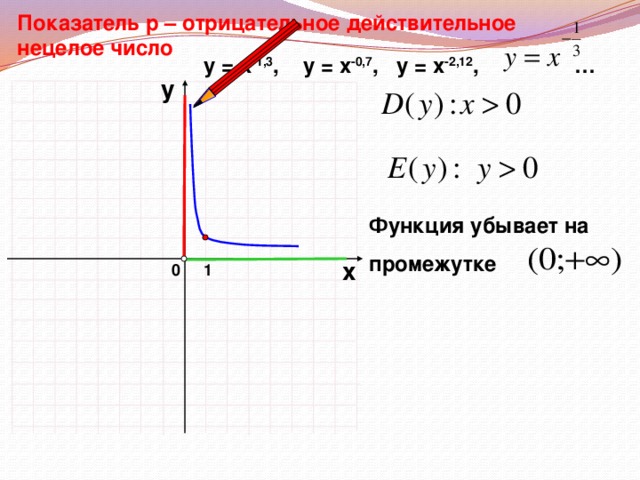
у = хр, где р – заданное действительное число.
Свойства и график степенной функции зависят от свойств степени с действительным показателем, и в частности от того, при каких значениях х и р имеет смысл степень хр.
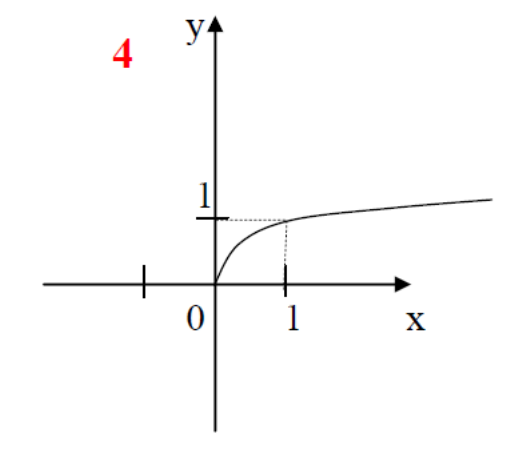
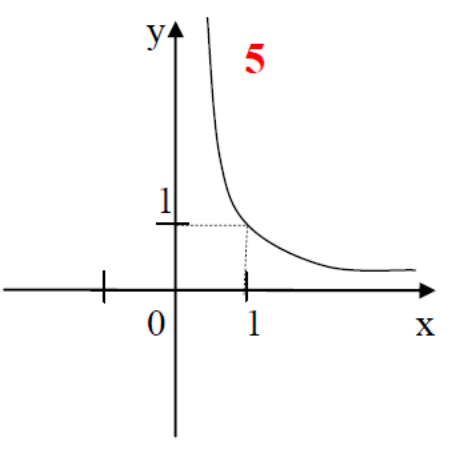
Сейчас каждый из вас будет оформлять опорный конспект по теме «Степенная функция». Заполнив этот конспект, вам будет удобно использовать его при подготовке к уроку. В опорном конспекте уже даны эскизы графиков. Ваша задача: сформулировать свойства функций и сделать записи в конспекте.
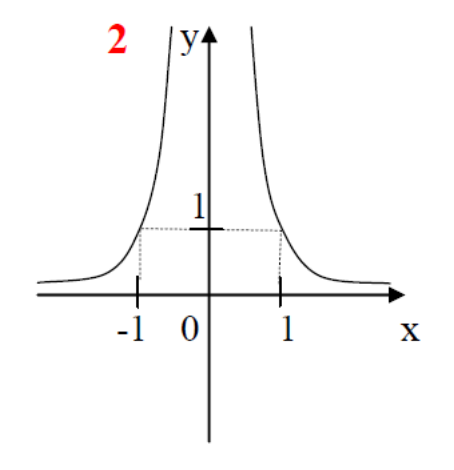
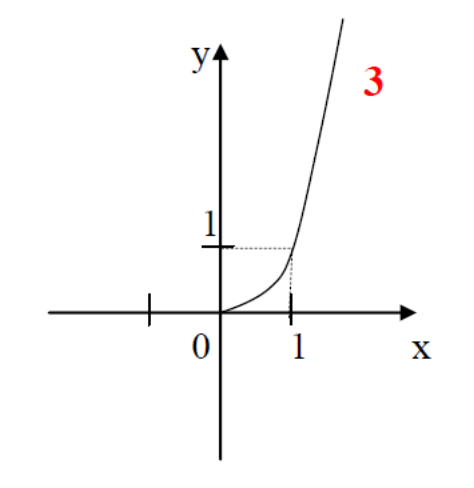
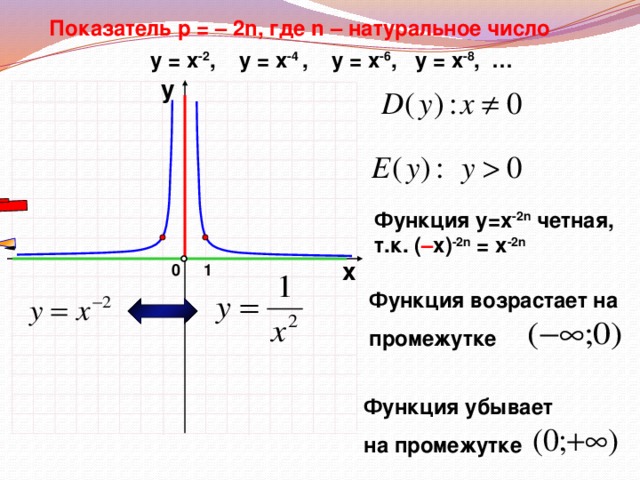
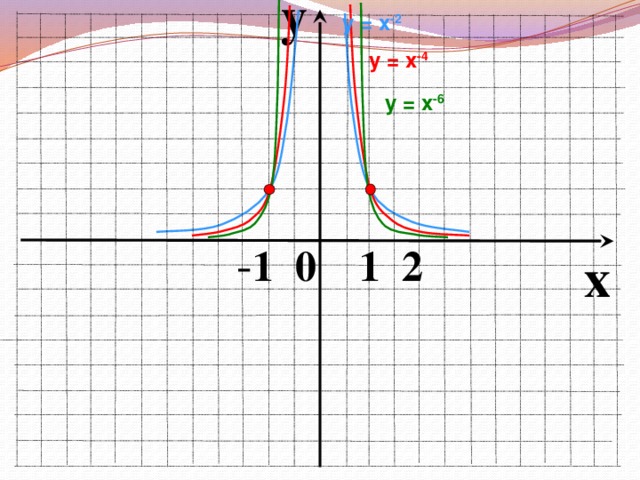
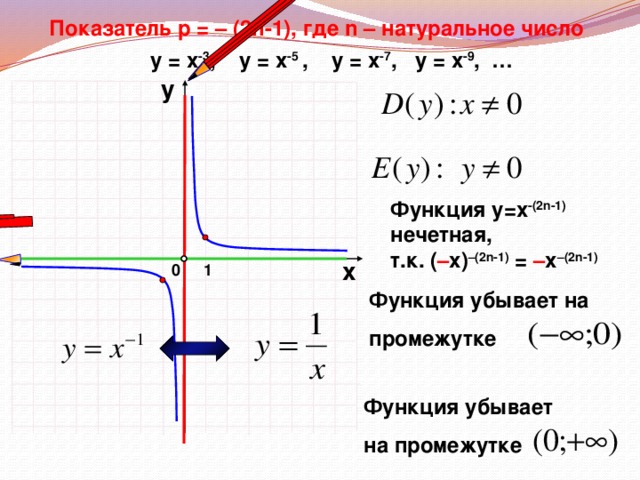
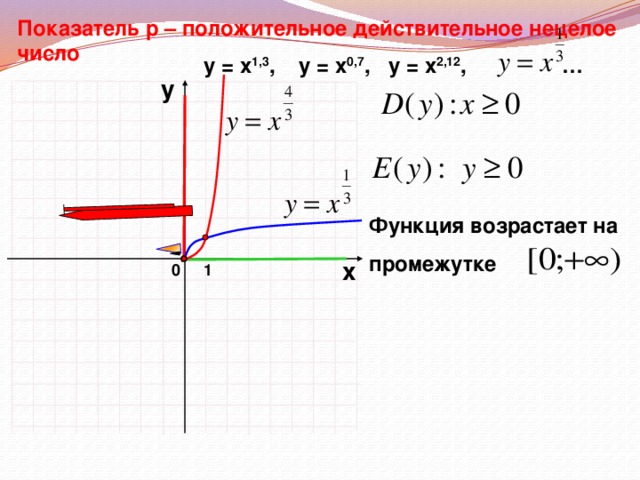
Слайды 5-17. Фронтальная работа с классом. Оформление записей в «Опорный конспект» (приложение 1). Перечисляем свойства функций по следующему плану.
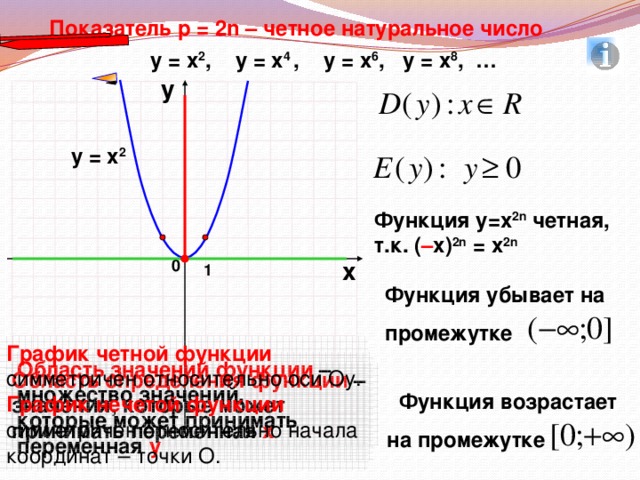
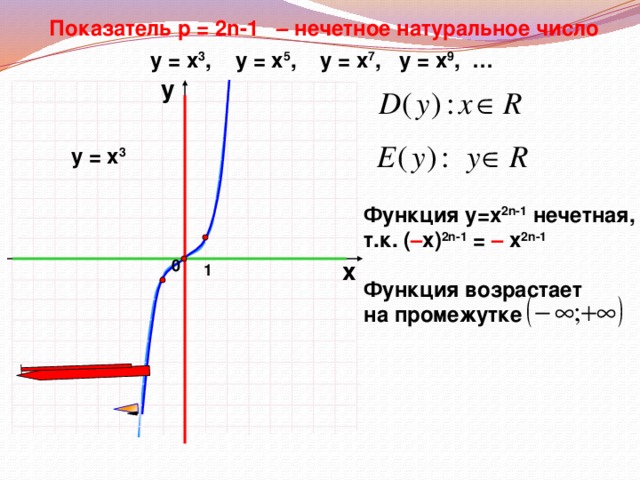
Область определения.
Область значений (множество значений).
Четность, нечетность функции. Графическая иллюстрация четной, нечетной функции. Аналитическая запись свойства четности, нечетности.
Записываем промежутки возрастания и убывания функции.
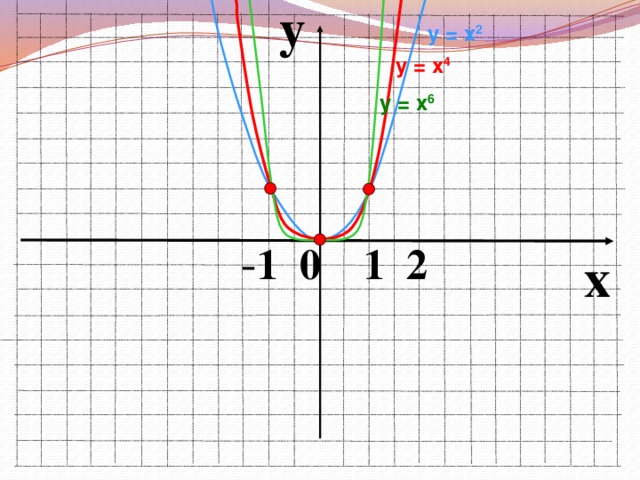
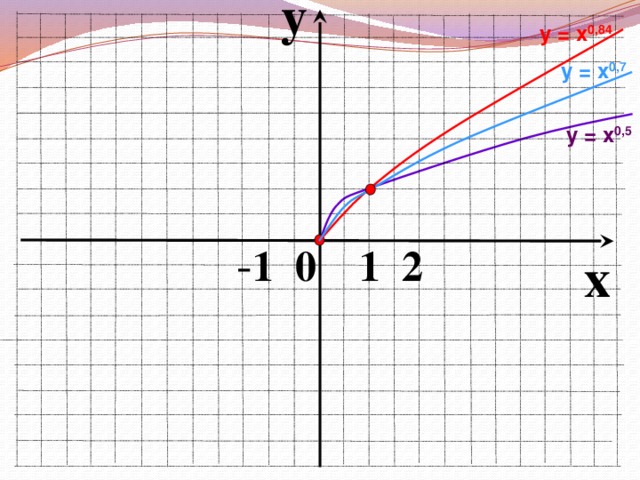
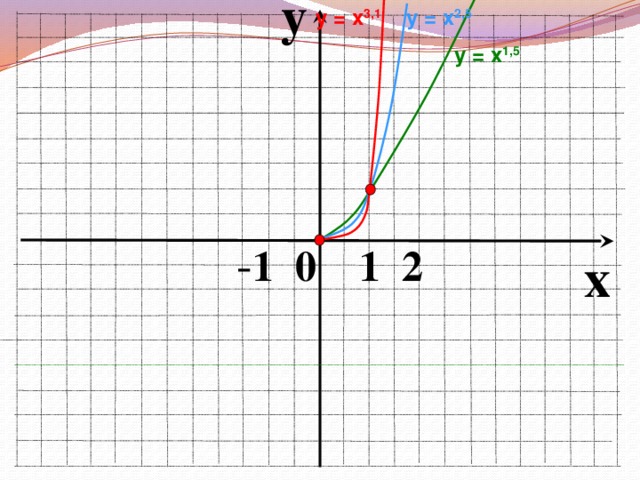
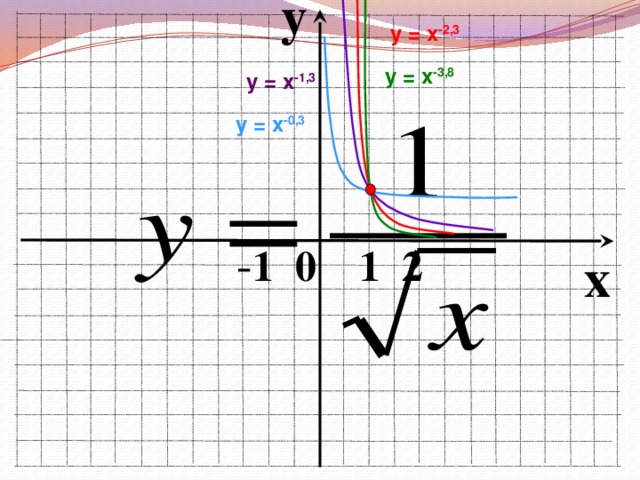
Во время фронтальной работы обращаю внимание на возможные варианты записи ответов в виде промежутков или неравенств. На слайдах 6, 8, 10, 12, 14, 15 демонстрирую, как изменяется вид графика при изменении показателя степени р.
4. Этап закрепления новых знаний 10 мин
Закрепление изученного материала. Решение упражнений из учебника.
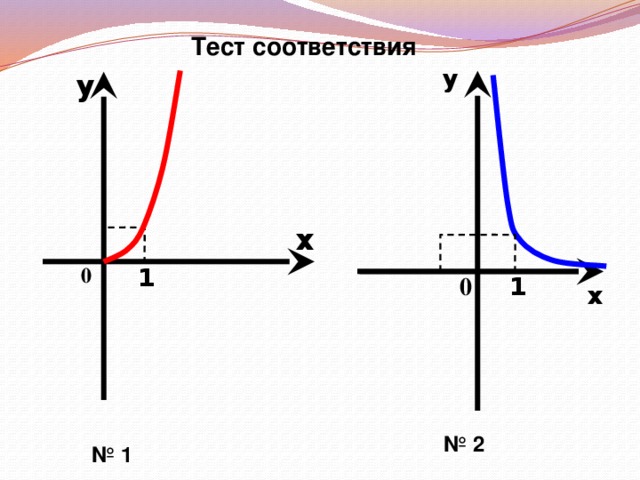
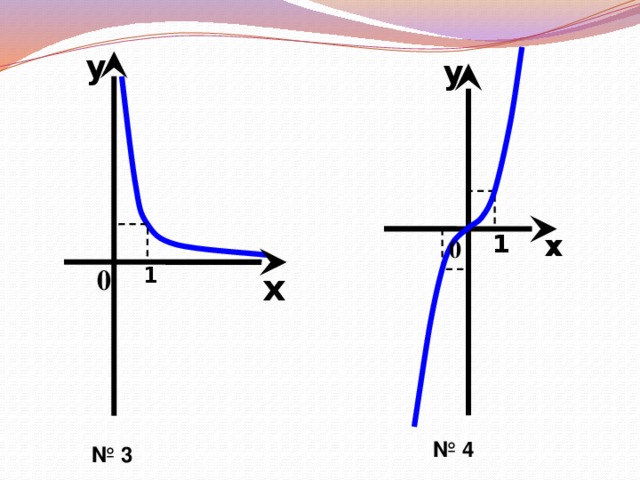
Мы вспомнили функции, которые нам знакомы, и увидели новые графики. Проверим, как вы усвоили новый материал. Проведем тест соответствия.
На партах у учащихся лежат набор карточек с формулами функций (приложение 3). Эскизы графиков воспроизводятся с помощью презентации. К доске приглашается по очереди 7 учащихся, которые должны привести в соответствие эскизы графиков и карточки с формулой, комментируя свой выбор. Ученик с помощью магнитов закрепляет таблички с формулами рядом с соответствующим номером графика.
Набор формул для учащихся.
у=х-0,4
у=х-9
у=х7
у=х8
у=х-6
у=х0,6
у=1
у=х1,8
у=х
Работа с учебником .
№ 125 (1, 3)
Доп № 126 (1).
5. Самостоятельная работа – тест соответствия «Степенная функция». 10 мин
Самостоятельная работа проводится в виде тестирования на ноутбуках. Работа идет парами. Учащиеся садятся за ноутбук вдвоем, открывают тест, записывают фамилии и проходят тест. Результат теста фиксируется в текстовом документе, после урока копируется и прикладывается к разработке урока.
степенная функция.mtf
Тест "Степенная функция"
Автор: Голубева Наталья Борисовна
Заключительная часть
6. Этап подведения итогов урока 3 мин
Подведение итогов урока, выставление оценок
7.Этап информации учащихся о домашнем задании и инструктаж к его выполнению 2 мин
По опорному конспекту – выучить свойства и графики.
№ 125(2,4), 128 .
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Приложение 2»
Просмотр содержимого документа
«Приложение 3 материал для повторения»
Просмотр содержимого документа
«Приложение 4»
Просмотр содержимого документа
«конспект урока Степенная функция, её свойства и график»
Просмотр содержимого документа
«тест степенная функция»
Просмотр содержимого презентации
«Приложение 1»
Полезное для учителя
Распродажа видеоуроков!
1740 руб.
2480 руб.
2000 руб.
2860 руб.
1630 руб.
2330 руб.
1970 руб.
2820 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
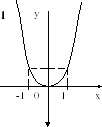
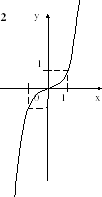





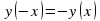 - нечетная функция
- нечетная функция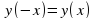 - четная функция
- четная функция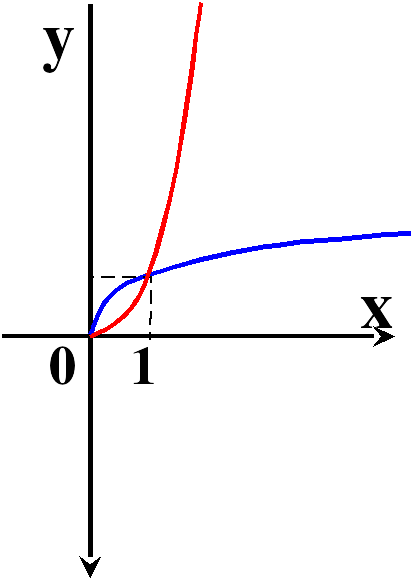

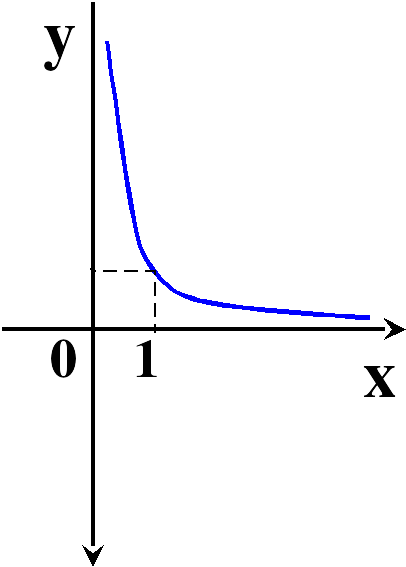
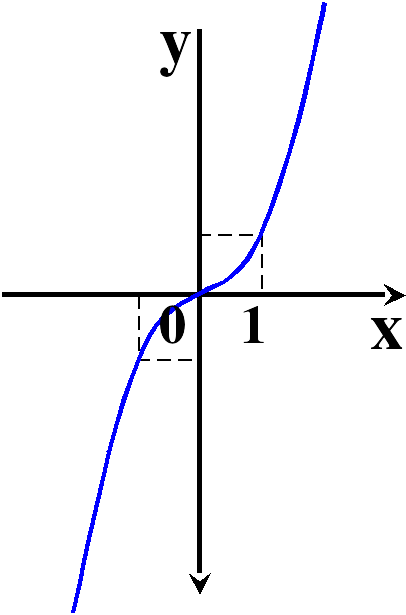
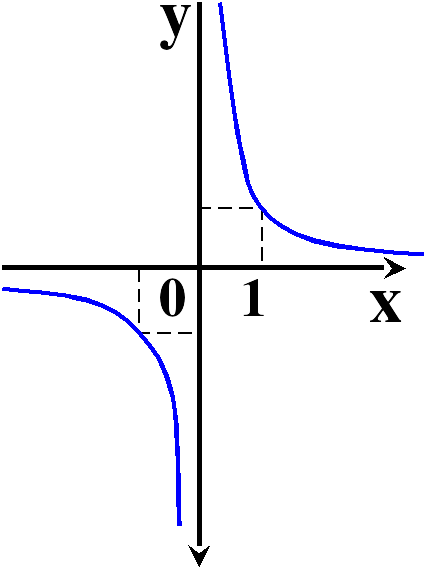

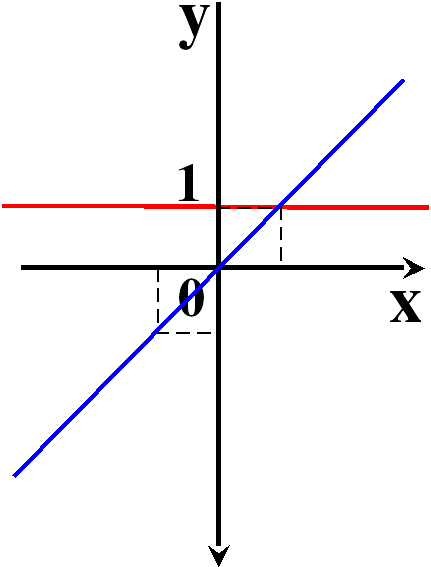
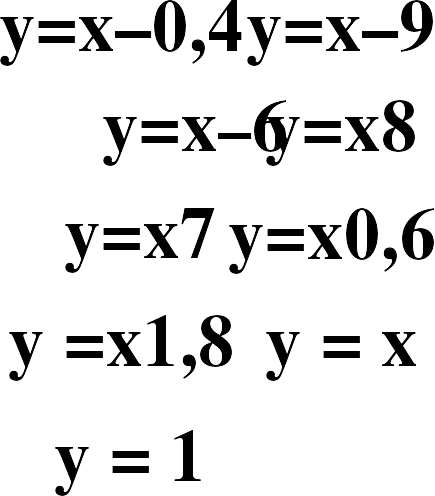
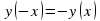 - нечетная функция
- нечетная функция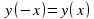 - четная функция)
- четная функция)