Степенная функция, ее свойства и график Демонстрационный материал Урок-лекция Понятие функции. Свойства функции. Степенная функция, ее свойства и график. - презентация.
Материал посвящен исследованию свойств степенной функции и построению её графиков и использованию готовых тестов (также можно использовать MS Excel или любую программу для построения графиков).
Просмотр содержимого документа
«Опорный конспект»
Просмотр содержимого презентации
«Свойства функции»
Просмотр содержимого презентации
«Степенная функция»

10 класс
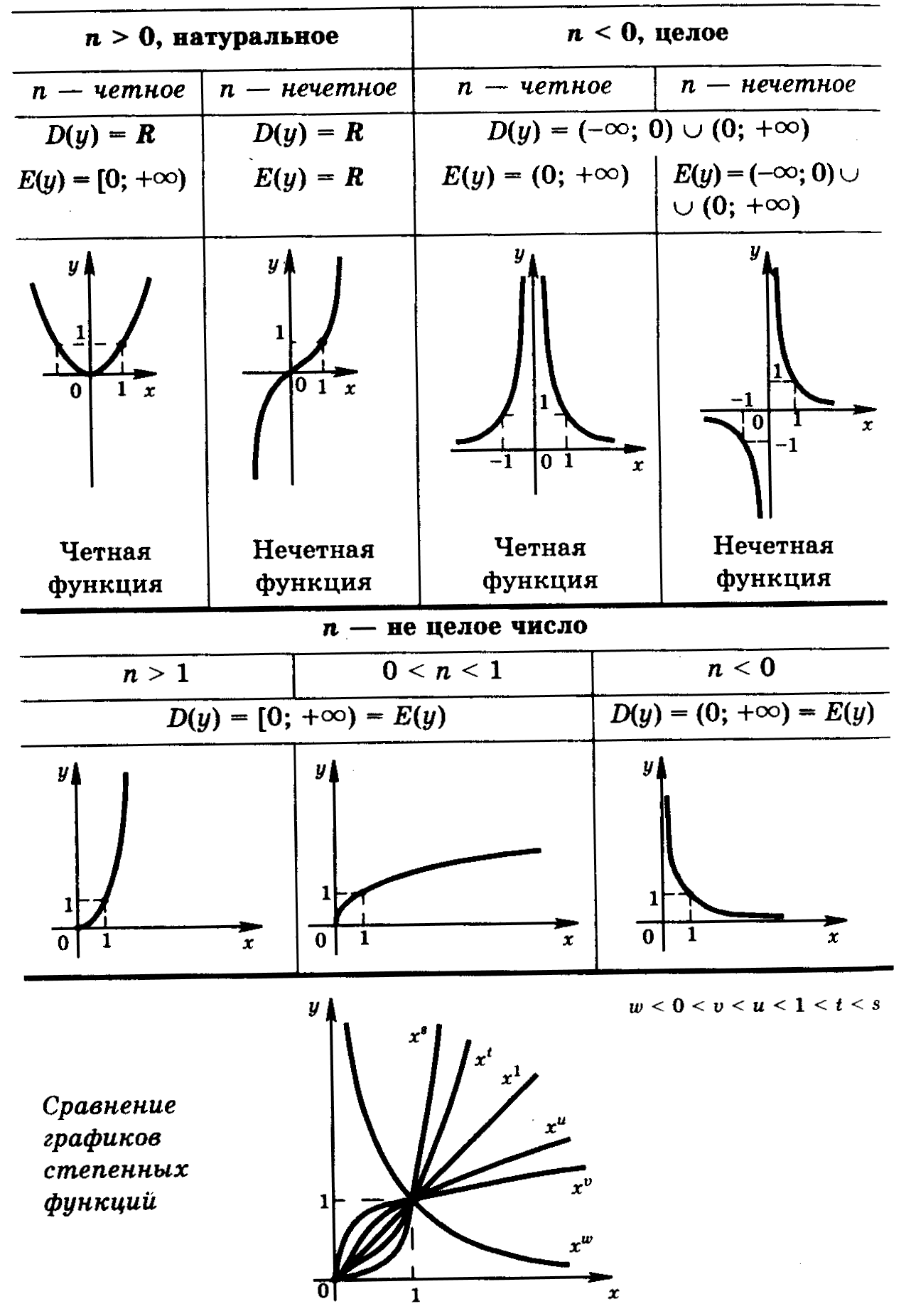
Степенная функция
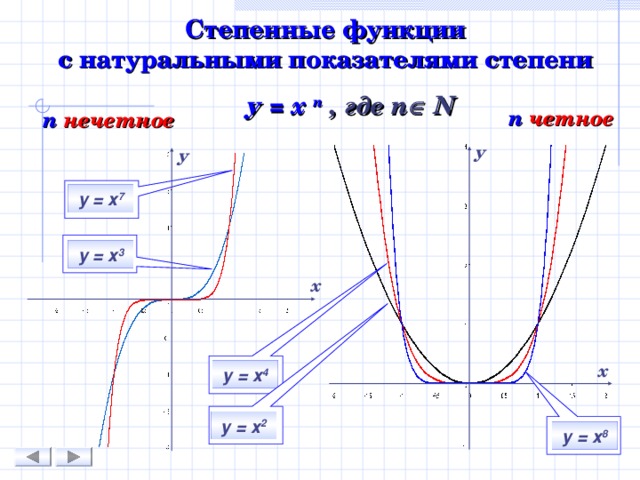
Степенные функции с натуральными показателями степени
у = х n , где n N
n четное
n нечетное
у
у
у = х 7
у = х 3
х
х
у = х 4
у = х 2
у = х 8
 0 на у (- ∞ ; + ∞) [ 0; + ∞) у(-х) = у(х), четная (- ∞ ; 0) (0; + ∞) Возрастание (убывание): Особые точки: убывает на (- ∞ ; 0 ] х возрастает на [ 0; + ∞) (-1; 1), (0; 0), (1; 1)" width="640"
0 на у (- ∞ ; + ∞) [ 0; + ∞) у(-х) = у(х), четная (- ∞ ; 0) (0; + ∞) Возрастание (убывание): Особые точки: убывает на (- ∞ ; 0 ] х возрастает на [ 0; + ∞) (-1; 1), (0; 0), (1; 1)" width="640"
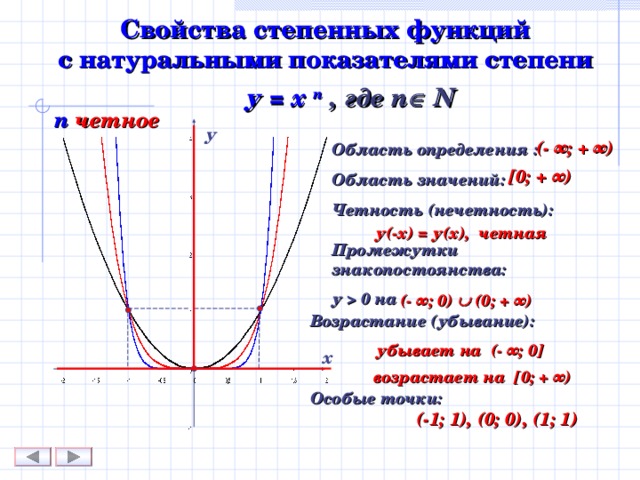
Свойства степенных функций с натуральными показателями степени
у = х n , где n N
n четное
Область определения : Область значений: Четность (нечетность): Промежутки знакопостоянства: у 0 на
у
(- ∞ ; + ∞)
[ 0; + ∞)
у(-х) = у(х), четная
(- ∞ ; 0) (0; + ∞)
Возрастание (убывание):
Особые точки:
убывает на (- ∞ ; 0 ]
х
возрастает на [ 0; + ∞)
(-1; 1), (0; 0), (1; 1)
 0 на у 0 на (- ∞ ; + ∞) у(-х) = - у(х), нечетная х (0; + ∞) (- ∞ ; 0) Возрастание (убывание): Особые точки: возрастает на (- ∞ ; + ∞) (-1; -1), (0; 0), (1; 1)" width="640"
0 на у 0 на (- ∞ ; + ∞) у(-х) = - у(х), нечетная х (0; + ∞) (- ∞ ; 0) Возрастание (убывание): Особые точки: возрастает на (- ∞ ; + ∞) (-1; -1), (0; 0), (1; 1)" width="640"
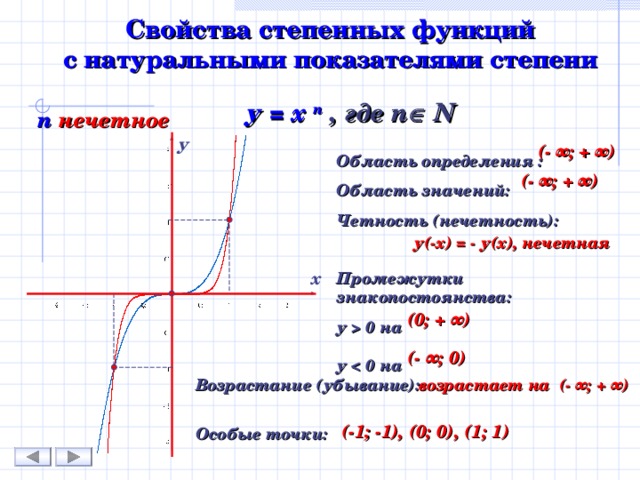
Свойства степенных функций с натуральными показателями степени
у = х n , где n N
n нечетное
у
(- ∞ ; + ∞)
Область определения : Область значений: Четность (нечетность): Промежутки знакопостоянства: у 0 на у 0 на
(- ∞ ; + ∞)
у(-х) = - у(х), нечетная
х
(0; + ∞)
(- ∞ ; 0)
Возрастание (убывание):
Особые точки:
возрастает на (- ∞ ; + ∞)
(-1; -1), (0; 0), (1; 1)
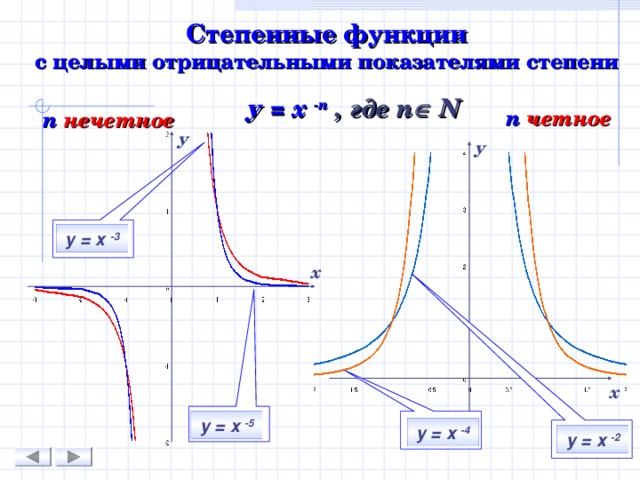
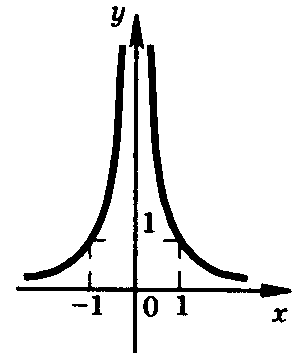
Степенные функции с целыми отрицательными показателями степени
у = х - n , где n N
n четное
n нечетное
у
у
у = х -3
х
х
у = х -5
у = х -4
у = х -2
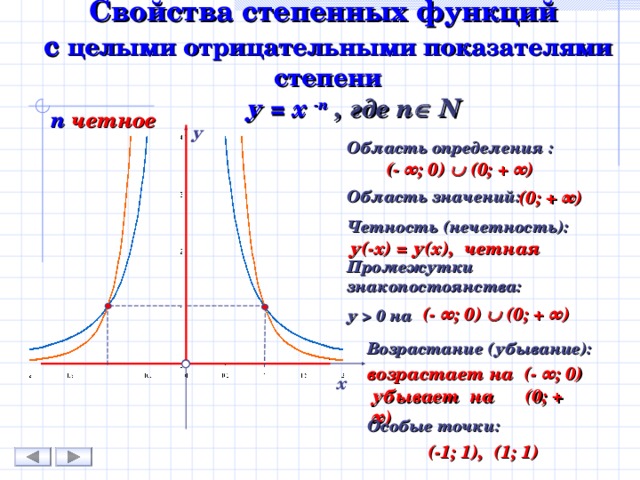 0 на (- ∞ ; 0) (0; + ∞) (0; + ∞) у(-х) = у(х), четная (- ∞ ; 0) (0; + ∞) Возрастание (убывание): Особые точки: возрастает на (- ∞ ; 0) х убывает на (0; + ∞) (-1; 1), (1; 1)" width="640"
0 на (- ∞ ; 0) (0; + ∞) (0; + ∞) у(-х) = у(х), четная (- ∞ ; 0) (0; + ∞) Возрастание (убывание): Особые точки: возрастает на (- ∞ ; 0) х убывает на (0; + ∞) (-1; 1), (1; 1)" width="640"
Свойства степенных функций с целыми отрицательными показателями степени
у = х - n , где n N
n четное
у
Область определения : Область значений: Четность (нечетность): Промежутки знакопостоянства: у 0 на
(- ∞ ; 0) (0; + ∞)
(0; + ∞)
у(-х) = у(х), четная
(- ∞ ; 0) (0; + ∞)
Возрастание (убывание):
Особые точки:
возрастает на (- ∞ ; 0)
х
убывает на (0; + ∞)
(-1; 1), (1; 1)
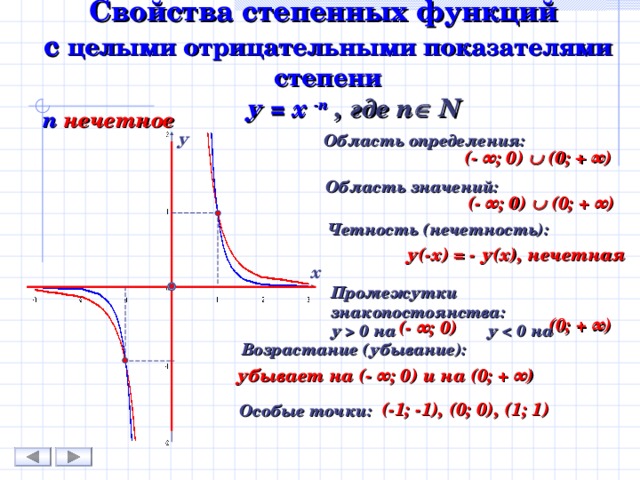 0 на у 0 на (0; + ∞) (- ∞ ; 0) Возрастание (убывание): убывает на (- ∞ ; 0) и на (0; + ∞) (-1; -1), (0; 0), (1; 1) Особые точки:" width="640"
0 на у 0 на (0; + ∞) (- ∞ ; 0) Возрастание (убывание): убывает на (- ∞ ; 0) и на (0; + ∞) (-1; -1), (0; 0), (1; 1) Особые точки:" width="640"
Свойства степенных функций с целыми отрицательными показателями степени
у = х - n , где n N
n нечетное
у
Область определения:
(- ∞ ; 0) (0; + ∞)
Область значений:
(- ∞ ; 0) (0; + ∞)
Четность (нечетность):
у(-х) = - у(х), нечетная
х
Промежутки знакопостоянства: у 0 на у 0 на
(0; + ∞)
(- ∞ ; 0)
Возрастание (убывание):
убывает на (- ∞ ; 0) и на (0; + ∞)
(-1; -1), (0; 0), (1; 1)
Особые точки:
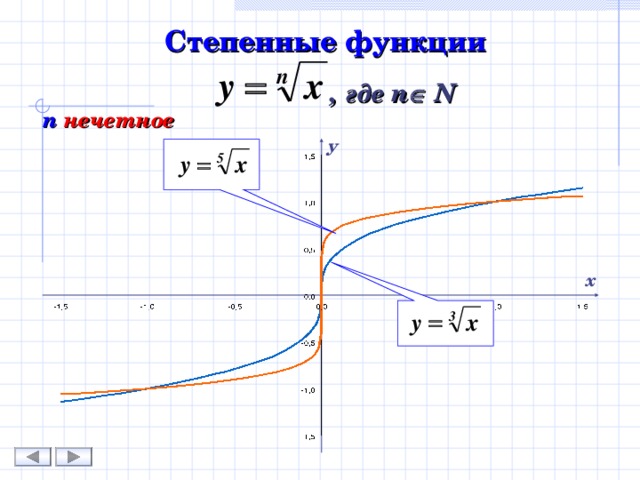
Степенные функции
, где n N
n нечетное
у
х
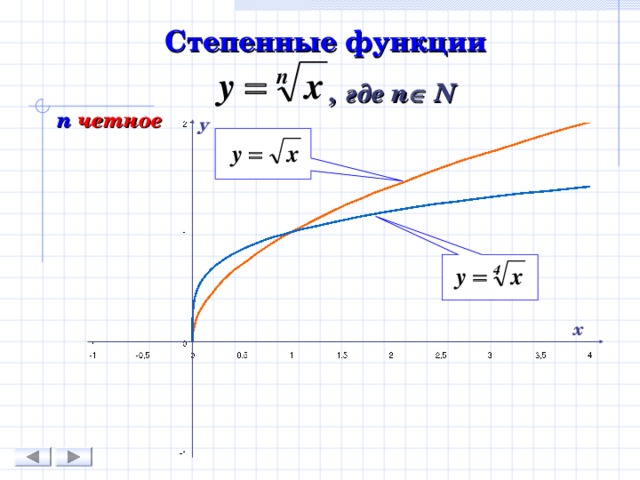
Степенные функции
, где n N
n четное
у
х
 0 на (- ∞ ; 0) у 0 (-1; -1), (0; 0), (1; 1) Особые точки:" width="640"
0 на (- ∞ ; 0) у 0 (-1; -1), (0; 0), (1; 1) Особые точки:" width="640"
Свойства степенных функций
, где n N
n нечетное
Область определения: Область значений:
(- ∞ ; + ∞)
у
(- ∞ ; + ∞)
Четность (нечетность):
х
у(-х) = - у(х), нечетная
Возрастание (убывание):
возрастает на (- ∞ ; + ∞)
Промежутки знакопостоянства:
на (0 ; + ∞)
у 0
на (- ∞ ; 0)
у 0
(-1; -1), (0; 0), (1; 1)
Особые точки:
 0 -------- у 0 Особые точки: (0; 0), (1; 1)" width="640"
0 -------- у 0 Особые точки: (0; 0), (1; 1)" width="640"
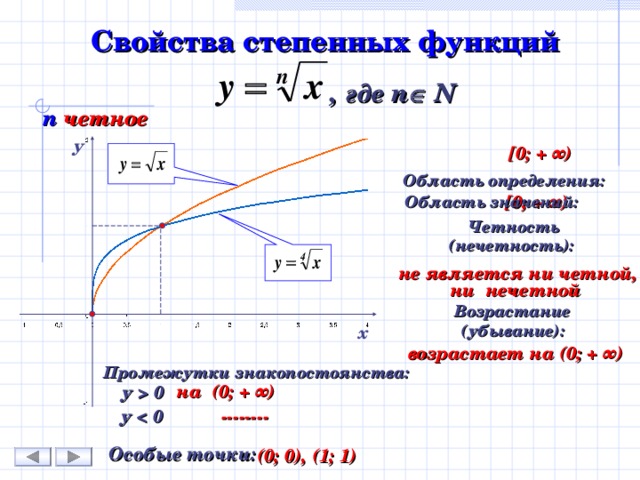
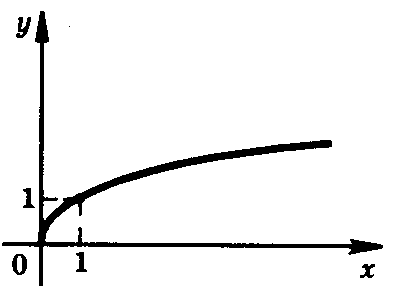
Свойства степенных функций
, где n N
n четное
Область определения:
у
[ 0; + ∞)
Область значений:
[ 0; + ∞)
Четность (нечетность):
не является ни четной, ни нечетной
Возрастание (убывание):
х
возрастает на ( 0; + ∞)
Промежутки знакопостоянства:
на (0 ; + ∞)
у 0
--------
у 0
Особые точки:
(0; 0), (1; 1)
 1, 0 а 1 у Область определения: (0; + ∞) Область значений: (0; + ∞) Четность (нечетность): не является ни четной, ни нечетной Возрастание (убывание): возрастает на (0; + ∞) Промежутки знакопостоянства: х (0 ; + ∞) у 0 Особые точки: (1; 1)" width="640"
1, 0 а 1 у Область определения: (0; + ∞) Область значений: (0; + ∞) Четность (нечетность): не является ни четной, ни нечетной Возрастание (убывание): возрастает на (0; + ∞) Промежутки знакопостоянства: х (0 ; + ∞) у 0 Особые точки: (1; 1)" width="640"
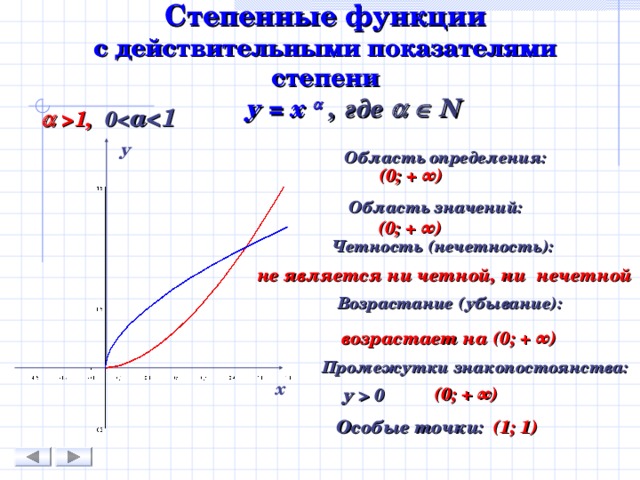
Степенные функции с действительными показателями степени
у = х , где N
1, 0 а 1
у
Область определения:
(0; + ∞)
Область значений:
(0; + ∞)
Четность (нечетность):
не является ни четной, ни нечетной
Возрастание (убывание):
возрастает на (0; + ∞)
Промежутки знакопостоянства:
х
(0 ; + ∞)
у 0
Особые точки:
(1; 1)
 0 Особые точки: (1; 1)" width="640"
0 Особые точки: (1; 1)" width="640"
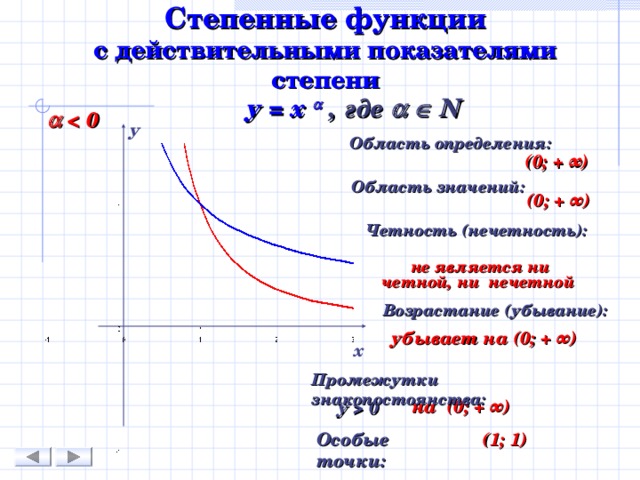
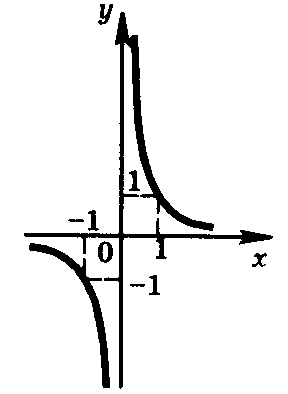
Степенные функции с действительными показателями степени
у = х , где N
0
у
Область определения:
( 0; + ∞)
Область значений:
( 0; + ∞)
Четность (нечетность):
не является ни четной, ни нечетной
Возрастание (убывание):
убывает на ( 0; + ∞)
х
Промежутки знакопостоянства:
на (0 ; + ∞)
у 0
Особые точки:
(1; 1)
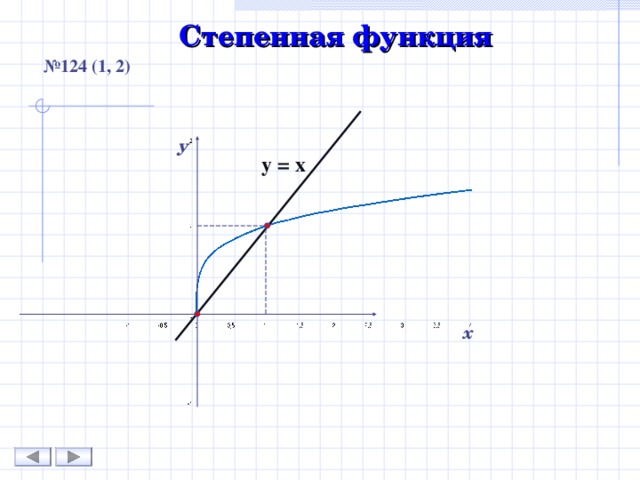
Степенная функция
№ 124 (1, 2)
у
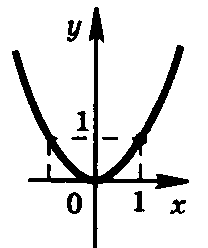
у = х
х
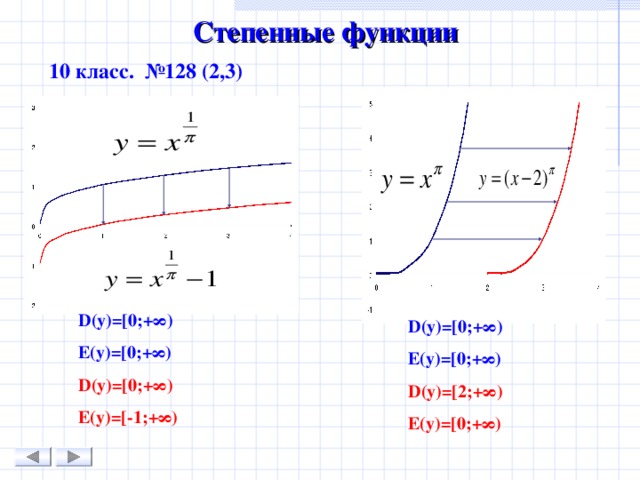
Степенные функции
10 класс. №128 (2,3)
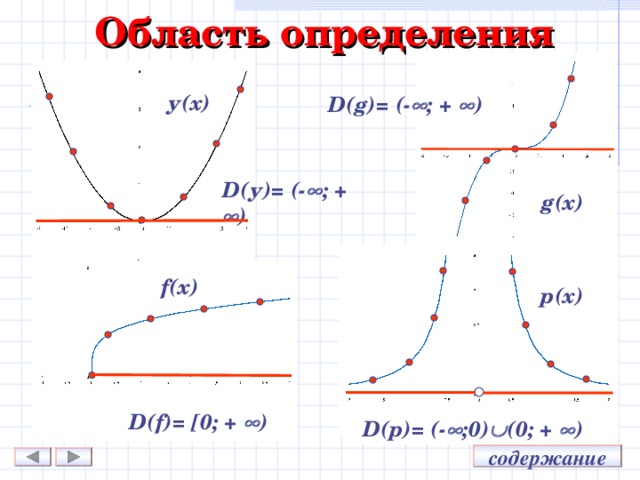
D(y)=[0 ; + ∞)
E(y)=[0 ; +∞)
D(y)=[0 ; +∞)
E(y) = [-1 ;+∞)
D(y)=[0 ; + ∞)
E(y)=[0 ; +∞)
D(y)=[ 2; +∞)
E(y) = [ 0;+∞)

Список литературы
- Алимов Ш.А. Алгебра и начала анализа: Учебник для 10-11 кл. общеобразовательных учреждений. – М.: Просвещение, 2005.
- Федорова Н.Е. Изучение алгебры и начал анализа в 10-11 классах. – М.: Просвещение, 2004.
- Генденштейн Л.Э., Ершова А.П., Ершова А.С. Наглядный справочник по алгебре и началам анализа с примерами для 7-11 классов. – М.: Илекса, Гимназия, 1997 .
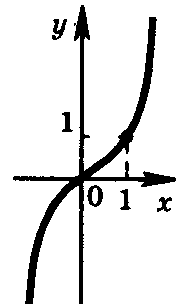
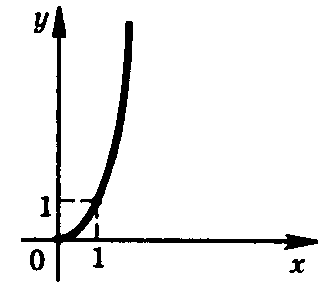
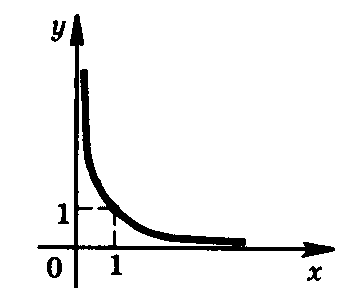

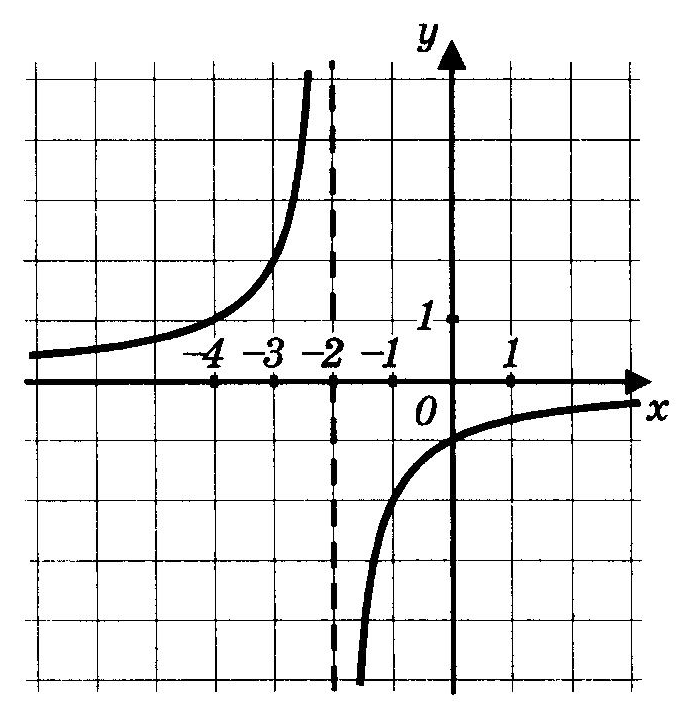


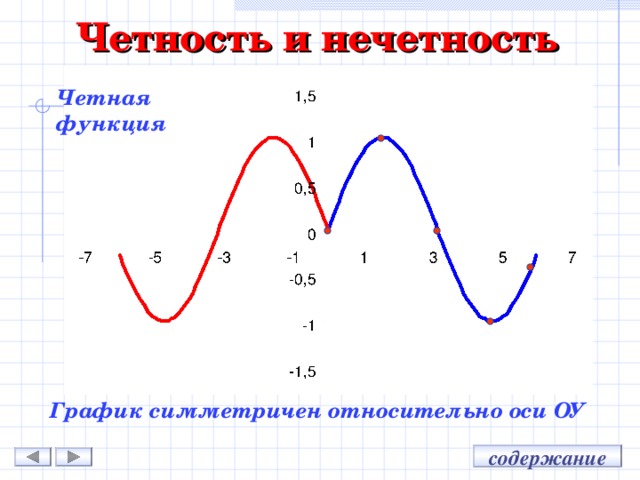
![Возрастание и убывание Промежуток возрастания: [-1 ; 1] [1 ; + ∞ ] (- ∞; - 1] и Промежутки убывания: содержание](https://fsd.kopilkaurokov.ru/uploads/user_file_55fa7d8b8b05a/img_user_file_55fa7d8b8b05a_1_3.jpg)
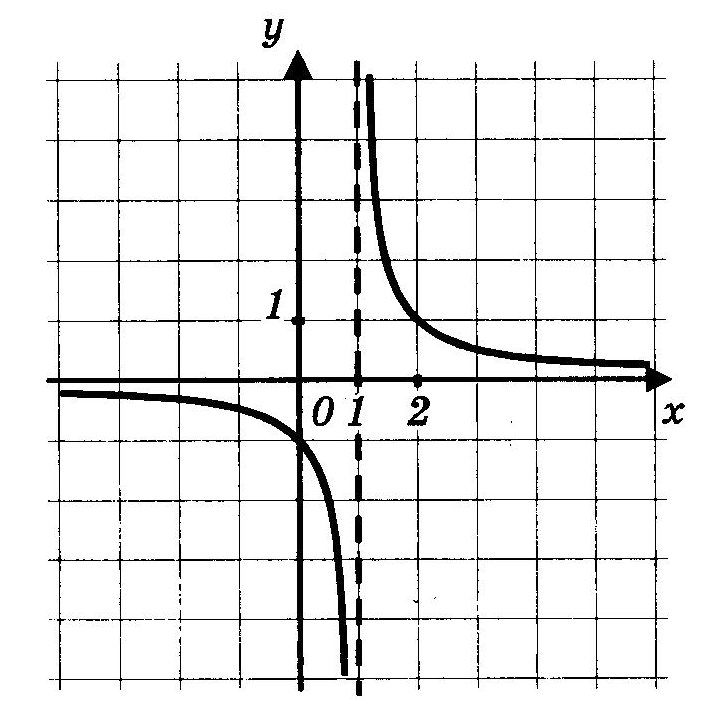
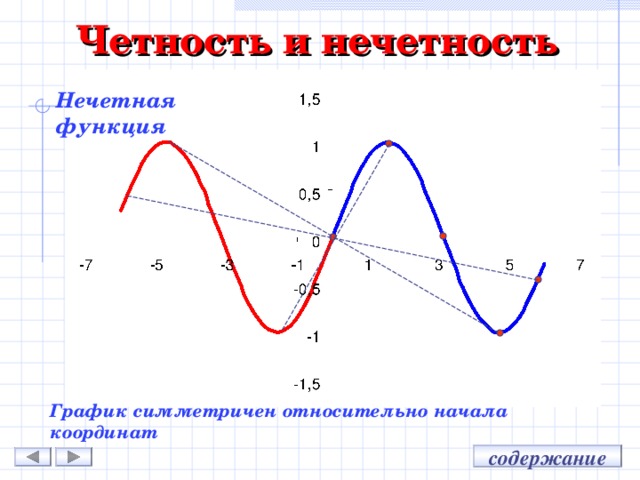
![Возрастание и убывание Промежуток убывания: [ 0; 2 ] [ 2; + ∞ ] (- ∞; 0 ] и Промежутки возрастания: содержание](https://fsd.kopilkaurokov.ru/uploads/user_file_55fa7d8b8b05a/img_user_file_55fa7d8b8b05a_1_4.jpg)



 0 на у (- ∞ ; + ∞) [ 0; + ∞) у(-х) = у(х), четная (- ∞ ; 0) (0; + ∞) Возрастание (убывание): Особые точки: убывает на (- ∞ ; 0 ] х возрастает на [ 0; + ∞) (-1; 1), (0; 0), (1; 1)" width="640"
0 на у (- ∞ ; + ∞) [ 0; + ∞) у(-х) = у(х), четная (- ∞ ; 0) (0; + ∞) Возрастание (убывание): Особые точки: убывает на (- ∞ ; 0 ] х возрастает на [ 0; + ∞) (-1; 1), (0; 0), (1; 1)" width="640"
 0 на у 0 на (- ∞ ; + ∞) у(-х) = - у(х), нечетная х (0; + ∞) (- ∞ ; 0) Возрастание (убывание): Особые точки: возрастает на (- ∞ ; + ∞) (-1; -1), (0; 0), (1; 1)" width="640"
0 на у 0 на (- ∞ ; + ∞) у(-х) = - у(х), нечетная х (0; + ∞) (- ∞ ; 0) Возрастание (убывание): Особые точки: возрастает на (- ∞ ; + ∞) (-1; -1), (0; 0), (1; 1)" width="640"

 0 на (- ∞ ; 0) (0; + ∞) (0; + ∞) у(-х) = у(х), четная (- ∞ ; 0) (0; + ∞) Возрастание (убывание): Особые точки: возрастает на (- ∞ ; 0) х убывает на (0; + ∞) (-1; 1), (1; 1)" width="640"
0 на (- ∞ ; 0) (0; + ∞) (0; + ∞) у(-х) = у(х), четная (- ∞ ; 0) (0; + ∞) Возрастание (убывание): Особые точки: возрастает на (- ∞ ; 0) х убывает на (0; + ∞) (-1; 1), (1; 1)" width="640"
 0 на у 0 на (0; + ∞) (- ∞ ; 0) Возрастание (убывание): убывает на (- ∞ ; 0) и на (0; + ∞) (-1; -1), (0; 0), (1; 1) Особые точки:" width="640"
0 на у 0 на (0; + ∞) (- ∞ ; 0) Возрастание (убывание): убывает на (- ∞ ; 0) и на (0; + ∞) (-1; -1), (0; 0), (1; 1) Особые точки:" width="640"


 0 на (- ∞ ; 0) у 0 (-1; -1), (0; 0), (1; 1) Особые точки:" width="640"
0 на (- ∞ ; 0) у 0 (-1; -1), (0; 0), (1; 1) Особые точки:" width="640"
 0 -------- у 0 Особые точки: (0; 0), (1; 1)" width="640"
0 -------- у 0 Особые точки: (0; 0), (1; 1)" width="640"
 1, 0 а 1 у Область определения: (0; + ∞) Область значений: (0; + ∞) Четность (нечетность): не является ни четной, ни нечетной Возрастание (убывание): возрастает на (0; + ∞) Промежутки знакопостоянства: х (0 ; + ∞) у 0 Особые точки: (1; 1)" width="640"
1, 0 а 1 у Область определения: (0; + ∞) Область значений: (0; + ∞) Четность (нечетность): не является ни четной, ни нечетной Возрастание (убывание): возрастает на (0; + ∞) Промежутки знакопостоянства: х (0 ; + ∞) у 0 Особые точки: (1; 1)" width="640"
 0 Особые точки: (1; 1)" width="640"
0 Особые точки: (1; 1)" width="640"



















