Урок №56. Логарифмические уравнения.
I этап. Актуализация (задания из пройденного материала, необходимые для усвоения новой темы).
Проверка домашнего задания. Итог предыдущего урока
Закончите определение логарифма: Логарифмом данного числа b по основанию а называется _____________________________________________________________
_______________________________________________________________________
3. Найдите значения выражения:
а) log27-log263+log236 = ____________________________________________________
_________________________________________________________________________
б) 252-log25 + 7-log73 = _______________________________________________________
_________________________________________________________________________
в) При каком основании выполняется равенство:
logx36=2 ________________________________________________________________
II этап. Самостоятельное изучение темы §17 стр 121-122 (перед объяснением новой темы представляется возможность для её самостоятельного усвоения с помощью учебника, приводятся задания, ответы на которые ученик должен найти из учебника и вписать в рабочую тетрадь).
Определение логарифмического уравнения:_________________________________
__________________________________________________________________________
Запишите общий вид логарифмического уравнения и его корня
I способ решения логарифмических уравнений (по определению логарифма)
П 1. logx(x2-5x+10)=3 ________________________________________________________
_______________________________ ___________________________________________
Проверка__________________________________________________________________
II способ решения логарифмических уравнений (приведение уравнения к виду loga f(x)= loga g(x) с последующим потенцированием)
П 2.lg(x+5)-lg(x2-25)=0______________________________________________________
__________________________________________________________________________
III способ введения новой переменной
П 3.log22x-log2x=0___________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
III этап. Разноуровневые задания.
1 уровень(5 баллов)
Образец решения уравнения
ln(3 x-5)=0
ОДЗ:
3х-5>0
3х>5
х>5/3
х>
ln(3x-5)=0
ln(3x-5)=ln1
3x-5=1
3x=1+5
3x=6
х=2 Отв: х=2
№1. Решите уравнения:
log7(4-x)=1
_____________________________________
_____________________________________
_____________________________________
lg(2x-1)=lg3
_____________________________________
_____________________________________
_____________________________________
№2. Решите уравнения:
log5(х+1)=log5(4x-5)
_____________________________________
_____________________________________
_____________________________________
log2(4-x)=log2(1-2x)
_____________________________________
_____________________________________
_____________________________________
2 уровень(4 балла)
№1. Решите уравнения:
ln(6-x)+lnx=ln5
_____________________________________
_____________________________________
_____________________________________
lgx+lg(x-3)=10
_____________________________________
_____________________________________
_____________________________________
№2. Найдите наибольший целый корень уравнения:
2log32x-7log3x+3=0
_____________________________________
_____________________________________
_____________________________________
log6(x2-2x)=1-log62
_____________________________________
_____________________________________
_____________________________________
3 уровень(3 бала)
№1. Решите логарифмические уравнения:
а) _____________________________________
_____________________________________
_____________________________________
b) _____________________________________
_____________________________________
_____________________________________
Домашнее задание: стр121-122 определение, способы 1-3 учить.
Решить задания
1 уровень №271(1), 272 (1),
2 уровень №273 (1), 274 (1),
3 уровень №278
Просмотр содержимого документа
«Решение логарифмических уравнении»
Урок №56. Логарифмические уравнения.
I этап. Актуализация (задания из пройденного материала, необходимые для усвоения новой темы).
Проверка домашнего задания. Итог предыдущего урока
Закончите определение логарифма: Логарифмом данного числа b по основанию а называется _____________________________________________________________
_______________________________________________________________________
3. Найдите значения выражения:
а) log2 7-log2 63+log2 36 = ____________________________________________________
_________________________________________________________________________
б) 252- log 2 5 + 7- log 7 3 = _______________________________________________________
_________________________________________________________________________
в) При каком основании выполняется равенство:
logx 36=2 ________________________________________________________________
II этап. Самостоятельное изучение темы §17 стр 121-122 (перед объяснением новой темы представляется возможность для её самостоятельного усвоения с помощью учебника, приводятся задания, ответы на которые ученик должен найти из учебника и вписать в рабочую тетрадь).
Определение логарифмического уравнения:_________________________________
__________________________________________________________________________
Запишите общий вид логарифмического уравнения
и его корня
I способ решения логарифмических уравнений (по определению логарифма)
П 1. logx (x2 -5x+10)=3 ________________________________________________________
_______________________________ ___________________________________________
Проверка__________________________________________________________________
II способ решения логарифмических уравнений (приведение уравнения к виду loga a
П 2.lg(x+5)-lg(x2 -25)=0______________________________________________________
__________________________________________________________________________
III способ введения новой переменной
П 3.log2 2 x-log2 x=0___________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
III этап. Разноуровневые задания.
1 уровень(5 баллов)
Образец решения уравнения
ln (3 x -5)=0
ОДЗ:
3х-50
3х5
х5/3
х
ln(3x-5)=0
ln(3x-5)=ln1
3x-5=1
3x=1+5
3x=6
х=2 Отв: х=2
№1. Решите уравнения:
log7 (4-x)=1
_____________________________________
_____________________________________
_____________________________________
lg(2x-1)=lg3
_____________________________________
_____________________________________
_____________________________________
№2. Решите уравнения:
log5 (х+1)=log5 (4x-5)
_____________________________________
_____________________________________
_____________________________________
log2 (4-x)=log2 (1-2x)
_____________________________________
_____________________________________
_____________________________________
2 уровень(4 балла)
№1. Решите уравнения:
ln(6-x)+lnx=ln5
_____________________________________
_____________________________________
_____________________________________
lgx+lg(x-3)=10
_____________________________________
_____________________________________
_____________________________________
№2. Найдите наибольший целый корень уравнения:
2log3 2 x-7log3 x+3=0
_____________________________________
_____________________________________
_____________________________________
log6 (x2 -2x)=1-log6 2
_____________________________________
_____________________________________
_____________________________________
3 уровень(3 бала)
№1. Решите логарифмические уравнения:
а)
_____________________________________
_____________________________________
b)
_____________________________________
_____________________________________
Домашнее задание: стр121-122 определение, способы 1-3 учить.
Решить задания
1 уровень №271(1), 272 (1),
2 уровень №273 (1), 274 (1),
3 уровень №278(1,3)


 _____________________________________
_____________________________________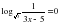 _____________________________________
_____________________________________















