Решение задач с помощью квадратных и рациональных уравнений

Конспект урока алгебры в 8 классе 

Тема: «Решение задач с помощью квадратных и рациональных уравнений». 

Цели:

Дидактическая:

Повторить определение квадратного уравнения, различные формулы для решения квадратных уравнений.

Рассмотреть различные типы задач, решаемые с помощью квадратных или рациональных уравнений, а также их систем. 

Воспитательная:

Развивать интерес учащихся к предмету математика. Стимулировать ребят к поиску различных способов решения задач. 

Ход урока

1. Математический диктант №1

2. Задача №1 (год создания группы) - решение задач у доски

3. Задача №2 (Степень популярности) - решение задач у доски

4. Задача №3 (Ходить полезно) - самостоятельно

5. Задача №4 (Увлечения) - решение парами

6. Решение квадратных уравнений (математический диктант
   №2)

Итог занятия

Математический диктант 

1 вариант 

1. Сформулируйте определение квадратного уравнения.
   2)Запишите пример неполного квадратного уравнения.
   3)Запишите, чему равен второй коэффициент в уравнении: 2х²+х-3=0
   4)Запишите, чему равны: а, в и с в уравнении -зх²+5х=0
   5) Сколько корней имеет неполное квадратное уравнение вида
   ах² +с = 0

1. Сколько корней имеет квадратное уравнение, если дискриминант положительный?

2. В каком случае квадратное уравнение имеет два равных корня?

3. Напишите формулу дискриминанта квадратного уравнения.

4. Напишите формулу корней квадратного уравнения со вторым четным коэффициентом. 10) Сформулируйте теорему Виета.
   11)Чему равна сумма корней квадратного уравнения ах² + вх + с = 0
   12) Приведите пример целого рационального уравнения.
   2 вариант
   
   1) Какое уравнение называют неполным квадратным уравнением?

1. Запишите пример квадратного уравнения.

2. Запишите, чему равен первый коэффициент в уравнении:
   -х² +4х-7 = 0

1. Запишите, чему равны: а, в, с в уравнении 5х² - 8 = 0 

2. Сколько корней может иметь неполное квадратное уравнение вида ах² +вх = о

3. Сколько корней имеет квадратное уравнение, если дискриминант отрицательный?

4. Какое уравнение называют приведенным квадратным уравнением?

5. Напишите формулу дискриминанта квадратного уравнения со вторым четным коэффициентом.

6. Напишите формулу корней квадратного уравнения.
   10) Чему равно произведение корней квадратного уравнения
   ах² +вх + с = О
   11) Сформулируйте теорему, обратную теореме Виета.
   12) Приведите пример дробного рационального уравнения.
   
   
   

Самопроверка

Первые 2 задачи решаем подробно (у доски)
Задача №1 Найдите год создания группы «Ранетки», если цифра единиц на 5 больше цифры десятков, количество десятков равно количеству сотен, количество тысяч на з меньше количества единиц, а произведение данного числа и суммы его цифр равно 14035 • Решение: Х-десятков и сотен, (х+5)-единиц, (х+2)-тысяч, (1000(х+2)+100х+10х+х+5)
-данное число, (х+2+х+х+х+5)-сумма цифр, произведение числа и суммы цифр-
(1000(х+2)+100х+10х+х+5)(4х+7)или14035
Уравнение: (1000(x+2)+100x+10x+x+5)(4x+7)=14035
(4444х+15797)х=0
х=0 или х=-15797:4444
Ответ: о-десятков, сотен, 5-единиц, 2-тысяч . 2005 год.

Задача №2. В один из грустных осенних дней группу «Ранетки»
слушали старшеклассники на переменах и 10 сотен студентов,
ехавших в автобусах и метро на лекции. Затем к ним присоединились 2 0 сотен студентов, подрабатывающих на разгрузке вагонов. В результате, количество старшеклассников в общей массе слушателей уменьшилось на 25%. Какое наибольшее количество старшеклассников могли в данный момент слушать «Ранеток»? 

Решение: х(сот.чел.)-старшеклассников и студентов слушали «Ранеток» вначале, (х-10)(сот.чел).- старшеклассников, (х+2о) сот.чел.-всего. ((х-10)/х)100 % составляют старшеклассники от первоначального количества людей,((х-10)/(х+20))100 %-составили старшеклассники от всего количества людей. 
((х-10)/х)100 - ((х-10)/(х+20))100 (%) или 25%.

Уравнение:




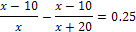
х² - 60х - 800 = О

х(х+20)≠0

Х=40 ИЛИ Х=20.

40-10=30 тыс. чел. старшеклассников слушали группу «Ранетки» Ответ: 30 тыс. чел.
Один из учащихся читает задачу №3. Он выполняет чертеж и предлагает идею решения.
Учащиеся доводят решение до конца самостоятельно. Первые 3 человека выполнивших задание, показывают решение учителю.
У остальных учащихся проверяют решение те учащиеся, у которых проверил учитель.

Задача №3 После репетиции песни «Стрела» Аня Руднева и Женя Огурцова отправились пешком на север Москвы со скоростью 5 км/ч, а Аня Байдовлетова и Лера Козлова - на восток со скоростью 6 км/ч. Через какое время расстояние между дуэтами будет 2 V61 км?
Через х часов расстояние будет 2 V6i(km), 5х (км)-
прошли Аня и Женя, 6х(км) прошли Аня и Лера.

Уравнение:
(5х)²+(6х)²= (2 √61)²
Х=±2
Ответ: через 2 часа.
Задачу №4 решают у доски.

Задача№4 Во время отдыха Лена Третьякова и Наташа Щелкова играют иногда в теннис на корте, длина которого вдвое больше ширины, а площадь равна 800 м² Найдите расстояние между девушками, если они встанут по диагонали прямоугольной площадки

Решение
х(м)-ширина, 2х(м)-длина, х(2х)(м²) или800м².
Уравнение:
2х²=8оо, х=20.
20м-ширина, 40м-длина,
Ответ: 20V5 ^м-


Диктант №2 « Решение квадратных уравнений»

1 Вариант

1. 3х²-х-2=о корни 1 и -2/з

2. 2х²+Зх+1=0 корни -1и -1/2

3. -2х²+5х-2=0 корни 2 и l/2

4. 19х²-362х+19=0 корни 19 и 1/19

5. -13x²+168x+13=0 корни 13и -1/13

6. 31x²-960x-31=0 корни 31 и -1/31
   2 Вариант

1. -6х²+4х+2=0 корни 1 и –2/3

2. 3х²+5х+2=0 корни -1 и -2/3

3. 5х²+2бх+5=0 корни -5 и-1/5

4. -21х²-442х-21=0 корни -21 И -1/21

5. 15х²+224х-15=0 корни -15 и 1/15

6. 25х²-б24х-25=0 корни 25 и -1/25
   Ребята используют формулы для решения 1 и 2 уравнения
   
   ах² + вх + с = O.
   
   1) если а+в+с=0, то х₁ = 1,х₂ = 
   2) если а+с=в, то х₁ = — 1, х₂ = -
   Для решения третьего уравнения применяется формула:
   
   если уравнение имеет вид ах² + (а² + 1)х + а = 0, то х₁ = —а, х₂ = -
   
   Четвертое уравнение решается по формуле:
   
   
   
   если ах² — (а² + 1)х + а = 0, то х₁ = а, х₂ = .
   Для решения пятого уравнения применяется формула:
   
   
   
   
   если ах² + (а² — 1)х — а = О, то х, = -а, х₂ = 
   
   Шестое уравнение решается, если
   
   ах² — (а² — 1)х — а = 0, то x_t = а, х₂ = - . 
   
   Работа в классе осуществляется следующим образом. На доске записаны уравнения. Ребята должны устно решить их и ответы записать в тетради рядом с соответствующим номером задания. Затем, под руководством учителя учащиеся осуществляют самопроверку и анализируют ошибки. 
   
   Задача №5 решается самостоятельно на основе задачи №3. Первые з человека показывают решение учителю.
   
   Один из решивших устно объясняет решение.
   
   
   
   

7. Итог занятия.