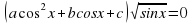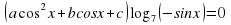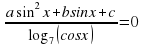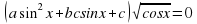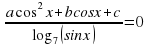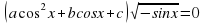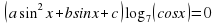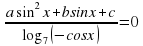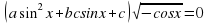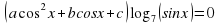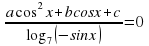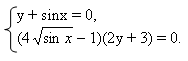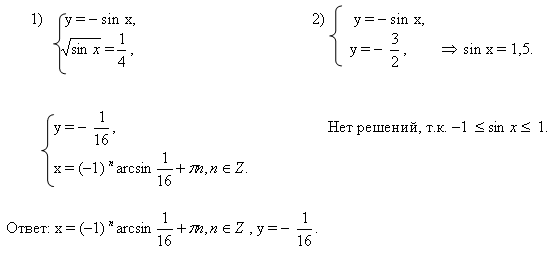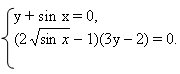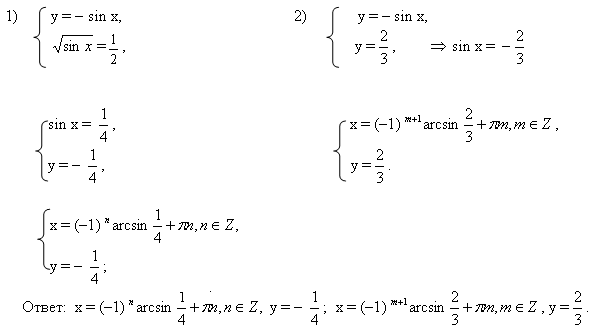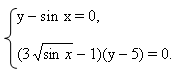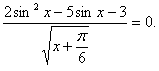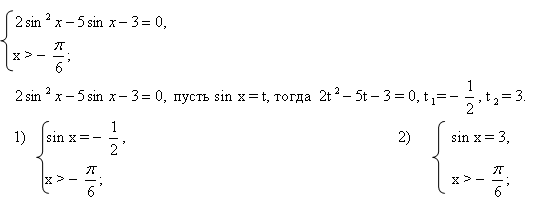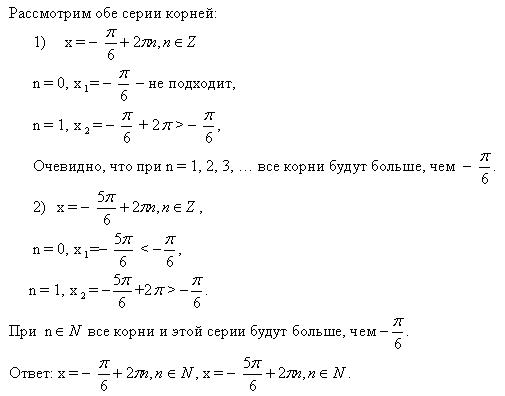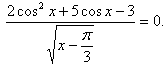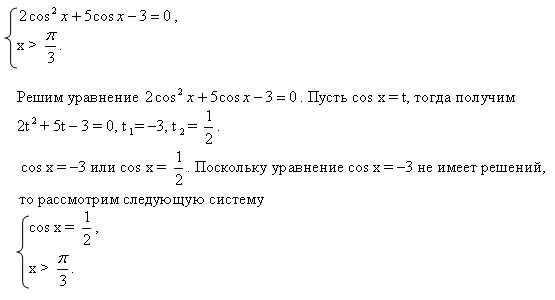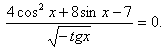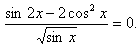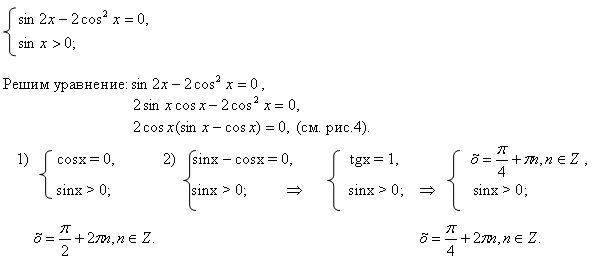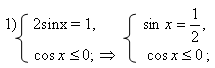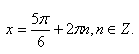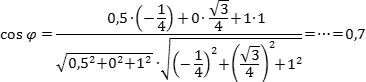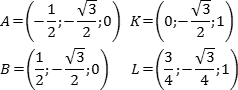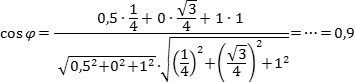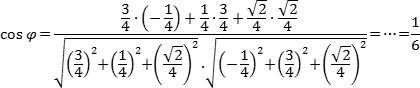Подготовка к ЕГЭ. Решение задач С1

Подготовка к ЕГЭ. Решение задач С1

Содержание

Введение 3

1.Особенности ЕГЭ по математике 2012 4

2.Совершенствование подготовки к ЕГЭ по решению задач С 1 8

Заключение 14

Список литературы 15

Приложения 17

Введение

Актуальность. В 2012 году задание С1 – это скорее всего тригонометрическое уравнение или система с явным или неявным отбором корней. Хотя в принципе это может быть уравнение любого другого вида из изучаемых в школе.

При серьезной подготовке надо научиться решать любые уравнения, а не только тригонометрические. Хотя бы потому, чтобы не ограничивать свои знания, чтобы подготовиться к успешному решению других задач, таких, как С3 и С5.

 Но исходя из того, что предлагается на экзаменах последних лет, а также в типовых экзаменационных вариантах, опубликованных ФИПИ, следует ожидать на ЕГЭ-2012 в качестве задания С1 именно тригонометрическое уравнение или систему уравнений. Кроме того, вид этих уравнений довольно однотипен. И если время уже “поджимает”, то обратить свое внимание следует именно на этот вид уравнений.

Из всех заданий вида С задание С1 является самым легким, с ним справляется около 20% всех выпускников, а примерно 40% получают за это задание 1 балл, т.е. выполняют часть задачи.

В связи с этим целью нашего исследования является совершенствование подготовки к ЕГЭ учащихся по решению задач С 1.

Задачи исследования:

1. Рассмотреть особенности ЕГЭ по математике  в 2012 году.

2. Рассмотреть особенности подготовки к ЕГЭ с помощью «виртуального учителя».

1.Особенности ЕГЭ по математике 2012

Новый ЕГЭ по математике стал более логичным. Задачи в части B теперь располагаются по возрастанию трудности — почти как в части C.

Содержание экзамена

Окончательная версия ЕГЭ по математике 2012 состоит из 20 задач, разделенных на две части:

Часть B — 14 простых задач, в которых требуется лишь указать ответ. Впрочем, последние задачи этой части не такие уж и простые. Например, B13 — это текстовая задача, которая традиционно считается «продвинутой». Дальше идет B14 — задача на производную. Тоже не подарок, поскольку такие задачи очень разнообразны, и для каждой требуется собственный алгоритм решения;

Часть C — 6 сложных задач, причем с каждым номером сложность нарастает. Простого ответа здесь уже недостаточно — нужно полное решение. Эти задачи рассчитаны на сильных учеников, хотя, к примеру, C1 вполне по зубам любому человеку. Но последние задачи — C5 и C6 — это, конечно, жестоко.

Все задачи части B оцениваются по 1 баллу. Задачи C1 и C2 дают по 2 балла, C3 и C4 — по 3 балла, и, наконец, C5 и C6 — по 4 балла. Итого 32 балла за весь экзамен.

Как и прежде, для получения аттестата достаточно набрать 5—6 баллов. [2]

В целом, экзамен не сильно отличается от образца 2011 года, но можно выделить следующее:

Появилась теория вероятностей.

Задачи по тригонометрии стали сложнее и разнообразнее.

Геометрии стало больше на одну задачу.

Часть B

Итак, часть B состоит из 14 относительно легких задач по всему школьному курсу математики. За каждую задачу дают по одному баллу, хотя сложность у них, мягко говоря, не одинаковая.

Задачи расположены по возрастанию сложности, поэтому решайте все подряд. Исключение — последние номера (B12—B14), в них все зависит от того, знаете вы соответствующий раздел математики или нет. Если не знаете — даже не приступайте к решению этих задач;

Задачи B1—B6 всегда очень легкие. Это тот минимум, за который точно выдают аттестат. Но не стоит расслабляться, иначе можно допустить глупые ошибки. И не надо торопиться: экзамен длится целых 4 часа, и времени на решение этих задач хватит;

Если позволяет время, дважды решите всю часть B, а затем сравните ответы. Это избавит вас от множества ошибок. Эту рекомендацию я повторяю из года в год, и те ученики, которые ей следуют, стабильно получают более высокие баллы.

Часть C

Здесь собраны 6 задач, которые рассчитаны на сильных учеников. Для решения хорошо нужно разобраться в школьном курсе математики, а в последних задачах (C5—C6) не обойтись без серьезной подготовки.

За эти 6 задач можно набрать 18 баллов — больше, чем за всю часть B.

Задача C1

Здесь предлагается решить тригонометрическое уравнение —, но которое все-таки чуть сложнее «табличных» sin x = a и cos x = a. При этом все задачи C1 состоят из 2 частей:

Собственно, решить тригонометрическое уравнение;

Указать корни, принадлежащие заданному отрезку.

Для решения требуется знать:

Формулы приведения. Например, в задаче B7 они будут очень кстати. Но если в B7 вполне можно обойтись и без формул приведения, то здесь без них никуда;[5]

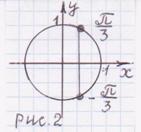
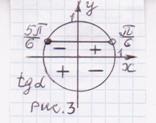
Знаки тригонометрических функций. Когда синус положительный? Когда отрицательный? А косинус? Без этих знаний решить C1 нельзя;

Периодичность тригонометрических функций — очень полезная вещь для решения второй части задачи (про корни на отрезке).

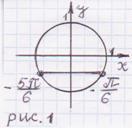
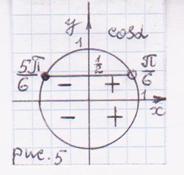
Корни на отрезке можно искать двумя способами: графическим и аналитическим. В первом случае строится график функции и отмечается искомый отрезок. Во втором — подставляются конкретные значения параметра в формулу общего корня. Оба решения правильны и вполне допустимы на экзамене.

Задача C2

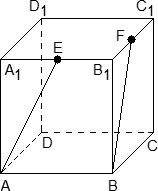
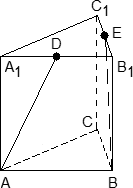
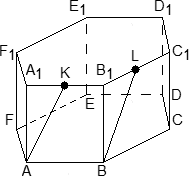
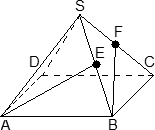
Это сложная задача по стереометрии. По условию, нам дан многогранник, в котором проведены дополнительные отрезки и сечения. Требуется найти угол между ними или, в крайнем случае, длину какого-нибудь отрезка.

Как и в предыдущей задаче, здесь можно действовать двумя способами:

Графический — нарисовать многогранник, отметить точки и рассчитать требуемую величину. Именно так учат решать задачи C2 в большинстве школ (если вообще учат);

Аналитический — добавить систему координат и свести задачу к векторам. Метод весьма нестандартный, но более надежный, поскольку большинство учеников лучше знают алгебру, чем геометрию.

Основное преимущество графического способа — наглядность. Достаточно выяснить расположение отрезков и плоскостей, после чего останется лишь немного посчитать.

Задача C3

Задача C3 — это логарифмическое или показательное неравенство. Во многих пробниках его заменяли иррациональным неравенством — в настоящем ЕГЭ такого не будет.[7]

В любом случае, исходное неравенство сводится к дробно-рациональному.

Задача C4

Еще одна геометрическая задача. На этот раз — планиметрия. В задаче C4 ученики столкнутся как минимум с двумя проблемами:

Придется выполнять довольно сложное геометрическое построение, которое требует хорошего знания теории и грамотной работы с чертежом;

Кроме того, в условии всегда присутствует неопределенность. Как правило, одна формулировка допускает две различные интерпретации. Соответственно, в задаче будет два разных ответа.

С другой стороны, никаких «сверхъестественных» знаний в этой задаче не требуется. Помимо геометрии, здесь надо знать тригонометрию, а в некоторых случаях — метод координат.

Задача C5

Например, многие задачи можно решить графически. Числа в уравнениях специально подобраны так, чтобы графики функций получались красивыми. Но возникает другой вопрос: как интерпретировать полученный результат? И что делать с параметром? Чтобы ответить на такие вопросы, требуется очень высокий уровень математической подготовки.

Задача C6

Это в некотором смысле уникальная задача, и не только для ЕГЭ по математике. По существу, задача C6 всегда решается очень просто — иногда всего в пару строчек. Вот только додуматься до этого решения очень трудно.

Как правило, в задаче C6 все рассуждения строятся вокруг целых чисел. Это классическая арифметика: признаки делимости, четность/нечетность, деление с остатком и прочее. Ничего сложного в этих правилах нет, но увидеть их — значит решить задачу. Или, как минимум, значительно продвинуться к ответу.[2]

Многие ученики отмечают, что задачи с факториалами решаются почти всегда. И наоборот, популярные в последнее время условия, начинающиеся с фразы «на доске написаны [...] чисел...», оказываются крайне трудными.

Очевидно, что составители C6 рассчитывают на учеников с очень высоким уровнем математической культуры. На тех, кто способен к весьма изощренным арифметическим выкладкам, кто обладает явной склонностью к изучению математики. Именно поэтому задачу C6 (как, впрочем, и C5) оценивают в 4 балла.

2.Совершенствование подготовки к ЕГЭ по решению задач С 1

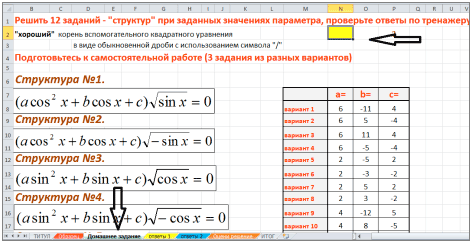
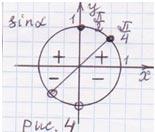
В данной работе представлен обучающий тренажер, созданный в программе Excel, по решению тригонометрических уравнений, которые в силу дополнительных условий, связанных с ОДЗ, предполагают необходимость производить отбор корней.

Цели:

• Способствовать формированию различных активных видов деятельности учащихся по подготовке к ЕГЭ по заданиям повышенного уровня сложности.

• Организовать “диалог” с компьютером по ходу решения задач, с целью осуществления проверки каждого шага решения. 

Задачи:

обучающая:

• формирование навыков решения тригонометрических уравнений с отбором корней;

• систематизация возможных ограничений, связанных с ОДЗ и влияющих на отбор корней;

• расширение видов деятельности по подготовке к ЕГЭ (в частности, ведение “диалога с компьютером”)

развивающая:

• способствовать развитию внимания, логического мышления, математической интуиции, умению анализировать и применять знания,

• воспитательная:

• побудить у учащихся осознание необходимости системной подготовки к ЕГЭ.

Выполнение тренажера рассчитано на 45-60 минут.

Рекомендуемый класс: 10-11

Средства обучения: персональные компьютеры для каждого учащегося.

Среда - Excel 2007

Возможные варианты применения тренажера и его модификации:

• В качестве “виртуального учителя” в рамках подготовки к ЕГЭ.

• Для самостоятельной работы с последующим обсуждением решений.

• В качестве самопроверки полученного решения.

• Для дистанционного обучения учащихся.

• Если все ячейки с комментариями и знаками вопроса сделать белым шрифтом (сделать невидимыми подсказки), то тренажер можно использовать для компьютерного контроля знаний

Тренажер предлагает три основных задания (в соответствии с традиционной методикой изучения нового материала).

В первом задании учащимся предлагается заполнять желтые клетки- пропуски по ходу решения основного уравнения и ответить на дополнительные вопросы. При этом тренажер осуществляет проверку каждого шага решения и предлагает некоторые комментарии к предложенным ответам.

Далее ученик должен выполнить свое индивидуальное задание - 12 тригонометрических уравнений, созданных на основе одного базового квадратного уравнения, с различными условиями на ОДЗ. В тренажере они названы структурами.

В тренажере предложено 28 вариантов-клонов. Вариант каждого ученика соответствует его номеру в классном журнале. Подставляя индивидуальные параметры в структуры уравнений, ученик получает свое индивидуальное задание.

		a=	b=	c=
	вариант 1	6	-11	4
	вариант 2	6	5	-4
	вариант 3	6	11	4
	вариант 4	6	-5	-4
	вариант 5	2	-5	2
	вариант 6	2	-3	-2
	вариант 7	2	5	2
	вариант 8	2	3	-2
	вариант 9	4	-12	5

Решив уравнения, ученик вводит ответы в соответствующие ячейки тренажера. По введенным записям тренажер осуществляет автоматическую проверку правильности ответов.

Для корректной работы тренажера НЕ ЗАБУДЬТЕ ЗАПОЛНИТЬ ЯЧЕЙКУ N2 на странице “Домашнее задание”. Так как соответствующее квадратное уравнение может иметь только один подходящий для данного задания корень, то именно он называется “хорошим”, его надо ввести в виде обыкновенной дроби с использованием символа “/”.

Если корень вспомогательного уравнения найден верно, то появится запись: “ Для проверки ответов перейдите на страницу ОТВЕТЫ ….” ( вместо многоточия будет стоять советующий номер страницы, в которую надо вводить ответы).

Форма записи ответа обуславливается спецификой программы Excel,в которой создан тренажер. Но недостатки программы можно легко превратить в ее достоинства, если просто обратить особое внимание на необходимость писать коэффициенты 0 или 1 перед множителем и на знаменатель 1 в записи целого числа.

В третьем задании учащимся предлагается оценить решение 10 уравнений данной тематики по критериям ЕГЭ. Для этого им следует просто поставить балл в желтую клетку рядом с соответствующим решением.

При правильном выставлении балла появляется комментарий поясняющий логику выставления данного балла с точки зрения его соответствия критериям ЕГЭ.

На итоговой странице тренажера автоматически выставляется отметка в зависимости от количества выполненных заданий

В завершении работы с заданиями данного типа можно предложить учащимся на уроке традиционную самостоятельную работу, содержащую 3 уравнения из разных структур с разными параметрами. Данный тренажер позволяет составить избыточное количество вариантов для подобной работы. А поскольку “хороших” корней основного квадратного уравнения всего два, то заполнив обе страницы ОТВЕТЫ 1 и ОТВЕТЫ 2 можно получить “ответник” для всех таких заданий.

Заключение

Что же необходимо знать для успешного решения задания С1?

1. Понимать, уметь “читать” числовую окружность.

2. Знать определения синуса, косинуса, тангенса и котангенса.

3. Значения тригонометрических функций основных аргументов.

4. Использую числовую окружность, уметь использовать свойства тригонометрических функций.

5. Уметь решать простейшие тригонометрические уравнения по формулам и с использованием числовой окружности.

6. Уметь решать простейшие тригонометрические неравенства, используя числовую окружность.

7. Уметь выбирать корни согласно условию задачи или по виду уравнения, для чего уметь находить области определения различных функций, заданных формулой.

8. Знать основные тригонометрические формулы.

9. Знать основные методы решения тригонометрических уравнений.

10. Уметь решать системы тригонометрических уравнений, правильно записывать ответ.

Работать над темой можно в соответствии со следующим планом:

1.  Числовая окружность.

2. Определение, значения и свойства синуса, косинуса, тангенса и котангенса.

3. Обратные тригонометрические функции

4. Простейшие тригонометрические уравнения.

5. Простейшие тригонометрические неравенства

6. Выбор корней при решении тригонометрических уравнений.

7. Методы решения тригонометрических уравнений.

8. Системы тригонометрических уравнений.

9. Примеры решения задания С1 из экзаменационных вариантов.

Список литературы

1. Алгебра и начала математического анализа. 10 класс. Контрольные работы. Профильный уровень. Глизбург В.И. -М.: Мнемозина, 2009. - 39 с.

2. Денищева Л.О., Глазков Ю.А., Крас-нянская К.А., Рязановский А.Р., Семенов П.В. Единый государственный экзамен 2008. Математика. Учебно-тренировочные материалы для подготов­ки учащихся / ФИПИ - М.: Интеллект-Центр, 2007.

3. ЕГЭ-2012. Математика: типовые эк­заменационные варианты: 30 вариантов / под ред. А.Л. Семенова, И.В. Ященко. -М.: Национальное образование, 2011. -192 с. (ЕГЭ-2012. ФИПИ - школе).

4. ЕГЭ-2011. Математика: типовые эк­заменационные варианты: 10 вариантов / под ред. А.Л. Семенова, И.В. Ященко. -М.: Национальное образование, 2010.

5. ЕГЭ 2012. Математика. Типовые тестовые задания /под ред. А.Л. Семено­ва, И.В. Ященко. - М.: Издательство «Эк­замен», 2012. - 51 с.

6. Единый государственный экзамен 2011. Математика. Универсальные мате­риалы для подготовки учащихся / ФИПИ

1. - М.: Интеллект-Центр, 2011.

1. Задачи письменного экзамена по ма­тематике за курс средней школы. Усло­вия и решения. Вып. 1-6, 8, 12, 14, 18, 25.

1. - М.: Школьная Пресса, - (Библиотека журнала «Математика в школе»), 1993­2003.

2. Корянов А.Г., Прокофьев А.А. Ма­тематика ЕГЭ 2011. Типовые задания С1. Отбор корней в тригонометрических уравнениях.http://alexlarin.net/ege/2011/C12011.pdf

1. Самое полное издание типовых ва­риантов заданий ЕГЭ: 2012: Математика / авт.-сост. И.Р. Высоцкий, Д.Д. Гущин, П.И. Захаров и др.; под ред. А.Л. Семено­ва, И.В. Ященко. - М.: АСТ: Астрель, 2011. - 93 с. (Федеральный институт пе­дагогических измерений).

1. Шестаков С.А., Захаров П.И. ЕГЭ 2011. Математика. Задача С1 / Под ред. А.Л. Семенова, И.В. Ященко. - М.: МЦН-МО, 2011.

1. www.alexlarin.narod.ru - сайт по оказанию информационной поддержки студентам и абитуриентам при подготовке к ЕГЭ, поступлению в ВУЗы и изучении различных разделов высшей математики.

2. http://eek.diary.ru/ - сайт по оказа­нию помощи абитуриентам, студентам, учителям по математике.

3. www.egemathem.ru - единый госу­дарственный экзамен (от А до Я).

Приложения

Структура заданий для самостоятельной работе по работе с

«Компьютерным учителем»Тригонометрические уравнения с отбором корней (задание С1)

Самостоятельная работа

ВАРИАНТ 1

1. 

2. 

3. 

ВАРИАНТ 2

1. 

2. 

3. 

ВАРИАНТ 3

1. 

2. 

3. 

ВАРИАНТ 4

1. 

2. 

3. 

Примеры решения заданий с 1

Решите систему уравнений

Решение.

Во втором уравнении системы произведение двух множителей равно нулю. Это возможно, если один из множителей равен нулю, а другой при этом имеет смысл. Рассмотрим два возможных случая:

2. Решите систему уравнений

Решение.

3. Решите систему уравнений

Решение.

4. Решите уравнение 

Решение.

Дробь равна нулю, когда числитель равен нулю, а знаменатель определен и не равен нулю.

Каждой точке единичной окружности                          соответствует множество углов.

Нет решений, т.к. – 1

(см. рис 1).
Необходимо «перебрать» корни и выбрать углы, большие . Воспользуемся ед. окружностью.

5. Решите уравнение

Решение.

На единичной окружности есть две точки, абсциссы которых равны (см. рис.2). Этим точкам соответствует множество углов. Из всех этих углов необходимо выбрать углы, большие чем  . Рассмотрим две серии корней:

6. Решите уравнение

Решение.

Дробь равна нулю, если числитель равен нулю, а знаменатель определен и не равен нулю.

Решать это уравнение лучше не по формуле, а с помощью окружности, учитывая при этом, что тангенс угла отрицателен, если угол лежит во II или в IV четверти (см.рис.3).

Решением уравнения являются две серии корней, но, поскольку тангенсы углов, лежащих в I четверти, положительны, то решением системы является одна серия корней 

Ответ:

7. Решите уравнение 

Решение.

8. Решите уравнение

Решение.

Произведение двух множителей равно нулю, если один из них равен нулю, а другой при этом имеет смысл.

для нахождения решения системы лучше воспользоваться  единичной окружностью (см. рис.5)

Решение.

9. Решите систему уравнений

Решение.

(Лучше проиллюстрировать на окружности).

15

Подготовка к ЕГЭ. Решение задач С2

Содержание

Введение 3

1.Актуальные вопросы подготовки к ЕГЭ 4

2.Задача C2 в  ЕГЭ 8

3.Традиционный метод решения 8

4.Метод координат в задаче C2 9

5.Примеры решения задач C2 в подготовке к ЕГЭ 11

Четырехугольная пирамида в задаче C2 15

Заключение 18

Список литературы 19

Введение

Актуальность. В 2012 уч.г. продолжается эксперимент по введению единого государственного экзамена (ЕГЭ), но уже в следующем учебном году такой экзамен пройдет не в рамках эксперимента.

Государственная итоговая аттестация в форме ЕГЭ позволяет оценить общую математическую подготовку учащихся. Самый большой плюс ЕГЭ: повысилась ответственность учителя, ученика и родителя за получения свидетельства. Экзамен принимает не тот учитель, который преподавал у выпускника, т.е. идея независимой экспертизы математических знаний, заложенная в ЕГЭ, хороша. Не секрет, что ученики имеют разный уровень обученности. Поэтому подготовить выпускника даже на уровень А весьма проблематично.

В связи с этим целью нашего исследования является подготовка к ЕГЭ. Решение задач С2.

Задачи исследования:

1. Рассмотреть особенности подготовки к ЕГЭ по математике.

2. Выделить особенности в подготовке к ЕГЭ в решение задач С 2.

3. Привести примеры решения задач С 2.

Методы исследования: теоретический анализ литературы по теме исследования.

1.Актуальные вопросы подготовки к ЕГЭ

Подготовленность к чему-либо понимается нами как комплекс приобретенных знаний, навыков, умений, качеств, позволяющих успешно выполнять определенную деятельность. В готовности учащихся к сдаче экзамена в форме ЕГЭ выделяют следующие составляющие:

• информационная готовность (информированность о правилах поведения на экзамене, информированность о правилах заполнения бланков и т.д.);

• предметная готовность или содержательная (готовность по определенному предмету, умение решать тестовые задания);

• психологическая готовность (состояние готовности – "настрой", внутренняя настроенность на определенное поведение, ориентированность на целесообразные действия, актуализация и приспособление возможностей личности для успешных действий в ситуации сдачи экзамена).

• Ориентируясь на данные компоненты, мы относим к актуальным вопросам подготовки к ЕГЭ следующие:

• организация информационной работы по подготовки учащихся к ЕГЭ;

• мониторинг качества;

• психологическая подготовка к ЕГЭ.[6]

Содержание информационной деятельности ОУ по вопросам ЕГЭ

В информационной деятельности образовательного учреждения по подготовке к ЕГЭ выделяют три направления: информационная работа с педагогами, с учащимися, с родителями.

Содержание информационной работы с педагогами.

1) Информирование учителей на производственных совещаниях 0

- нормативно-правовыми документами по ЕГЭ;

- о ходе подготовки к ЕГЭ в школе, в районе и области;

2) Включение в планы работы школьных методических объединений (ШМО) следующих вопросов:

- проведение пробных ЕГЭ, обсуждение результатов пробных ЕГЭ;

- творческая презентация опыта по подготовки учащихся к ЕГЭ (на методической или научной конференции в рамках школы);

- выработка совместных рекомендаций учителю-предметнику по стратегиям подготовки учащихся к ЕГЭ (с учетом психологических особенностей учащихся);

- психологические особенности 11-классников.

3) Педагогический совет "ЕГЭ – методические подходы к подготовке учащихся".

4) Направление учителей на районные и областные семинары и курсы по вопросам ЕГЭ.

Содержание информационной работы с учащимися.

1) Организация информационной работы в форме инструктажа учащихся:

- правила поведения на экзамене;

- правила заполнения бланков;

- расписание работы кабинета информатики (часы свободного доступа к ресурсам Интернет).

2) Информационный стенд для учащихся: нормативные документы, бланки, правила заполнения бланков, ресурсы Интернет по вопросам ЕГЭ.

3) Проведение занятий по тренировке заполнения бланков.

4) Пробные внутришкольные ЕГЭ по различным предметам.

5) В библиотеке:

- папка с материалами по ЕГЭ (нормативные документы, бланки по различным предметам, правила заполнения бланков, инструкции, ресурсы Интернет по вопросам ЕГЭ, перечень ресурсов библиотеки, рекомендации по подготовке к экзаменам);

- стенд с пособиями по ЕГЭ.[2]

Содержание информационной работы с родителями учащихся

1) Родительские собрания:

- информирование родителей о процедуре ЕГЭ, особенностях подготовки к тестовой форме сдачи экзаменов. Информирование о ресурсах Интернет;

- информирование о результатах пробного внутришкольного ЕГЭ (декабрь).

- пункт проведения экзамена, вопросы проведения пробного ЕГЭ в апреле.

2) Индивидуальное консультирование родителей (классные руководители, педагог-психолог).

Мониторинг качества образования

Особое внимание в процессе деятельности ОУ по подготовке учащихся к ЕГЭ занимает мониторинг качества обученности по предметам, которые учащихся будут сдавать в форме и по материалам ЕГЭ.

Мониторинг – отслеживание, диагностика, прогнозирование результатов деятельности, предупреждающие неправомерную оценку события, факта по данным единичного измерения (оценивания) (по: И. Ивлиева, В. Панасюк, Е. Чернышева). [1]

Мониторинг качества образования – "следящая" и в определенной степени контрольно-регулирующая система по отношению к качеству образования. Поэтому он одновременно есть, с одной стороны, подсистема системы управления качеством образования, а, с другой стороны информационная система, в которой циркулирует, собирается, обрабатывается, хранится, анализируется, представляется (визуализируется) информация о качестве образования (по: А.И. Субетто). [5]

Мониторинг качества образования – комплекс информационно-оценочных средств и структурированных процессов по поводу состояния качества системы образования (по: В.И. Воротилов, В.А. Исаев).

Система мероприятий по повышению качества подготовки учащихся к итоговой аттестации в форме ЕГЭ включает следующие направления деятельности:

- посещение администрацией уроков учителей-предметников, методическая помощь;

- включение в планы работы деятельности школьных методических объединений вопросов подготовки к ЕГЭ, дополнительные семинары, курсы повышения квалификации;

- индивидуальные консультации учителей-предметников для учащихся;

- привлечение ресурсов дистанционного обучения и ресурсов Интернет для подготовки к ЕГЭ;

- широкий спектр элективных курсов, расширяющих программу базового обучения;

- психологическая поддержка учащихся, консультирование, выработка индивидуальных стратегий подготовки к ЕГЭ.

Мониторинг качества должен быть системным и комплексным. По нашему мнению, он должен включать следующие параметры: контроль текущих оценок по предметам, выбираемым учащимися в форме ЕГЭ, оценок по контрольным работам, оценок по самостоятельным работам, результаты пробного внутришкольного ЕГЭ. Такую работу проводит заместитель директора, ответственный за вопросы ЕГЭ, анализирует их, выносит на обсуждение на административные и производственные совещания, доводит до сведения родителей. Мониторинг обеспечивает возможность прогнозирования оценок на выпускном ЕГЭ.[5]

Психологическая подготовка к ЕГЭ

Психологическая подготовка учащихся может осуществляться в форме спецкурса (или элективного курса). Цели такого курса: отработка стратегии и тактики поведения в период подготовки к экзамену; обучение навыкам саморегуляции, самоконтроля, повышение уверенности в себе, в своих силах.

Методы проведения занятий разнообразны: групповая дискуссия, игровые методы, медитативные техники, анкетирование, мини-лекции, творческая работа, устные или письменные размышления по предложенной тематике. Содержание занятий должно ориентироваться на следующие вопросы: как подготовиться к экзаменам, поведение на экзамене, способы снятия нервно-психического напряжения, как противостоять стрессу.

Работа с учащимися проводится по желанию учащихся – со всем классом или выборочно.

Педагог-психолог может проводить индивидуальные консультации для учащихся по вопросам подготовки к экзаменам.

Опыт показывает, что вопросы подготовки к ЕГЭ решаемы, если деятельность базируется на принципах:

- системности (подготовка ведется последовательно, функционирует команда специалистов, подготавливающая учащихся по различным направлениям – информационно, предметно, психологически);

- гибкости (отслеживание изменений нормативно-правовой базы, накопление научно-методических материалов по вопросам ЕГЭ, индивидуальный подход к каждому учащемуся).

2.Задача C2 в  ЕГЭ

В задаче C2 рассматриваются многогранники, на основе которых, как правило, нужно найти одну из следующих величин:

• Угол между скрещивающимися прямыми — это угол между двумя прямыми, которые пересекаются в одной точке и параллельны данным прямым.

• Угол между прямой и плоскостью — это угол между самой прямой и ее проекцией на данную плоскость.

• Угол между двумя плоскостями — это угол между прямыми, которые лежат в данных плоскостях и перпендикулярны линии пересечения этих плоскостей.

Прямые всегда задаются двумя точками на поверхности или внутри многогранника, а плоскости — тремя. Сами многогранники всегда задаются длинами своих граней.

3.Традиционный метод решения

В школьном курсе стереометрии упор делается на дополнительные построения, которые позволяют выделить искомый угол, а затем рассчитать его величину.

Здесь уместно вспомнить задачи на построение сечений многогранников, которые рассматриваются в 10 классе и у многих вызывают трудности. Существование формального алгоритма для таких построений совершенно не облегчает задачу, поскольку каждый случай достаточно уникален, а любая систематизация лишь усложняют процесс.

Именно поэтому задача C2 оценивается в два балла. Первый балл дается за правильные построения, а второй — за правильные вычисления и собственно ответ.

Преимущества традиционного решения:

• Высокая наглядность дополнительных построений, которые подробно изучаются на уроках геометрии в 10-11 классах;

• При правильном подходе значительно сокращается объем вычислений.

• Недостатки:

• Необходимо знать большое количество формул из стереометрии и планиметрии;

• Дополнительные построения каждый раз приходится придумывать «с нуля». И это может оказаться серьезной проблемой даже для хорошо подготовленных учеников.

Впрочем, если у читателя хорошее стереометрическое воображение, проблем с дополнительными построениями не возникнет. Остальным предлагаю отказаться от традиционного геометрического метода и рассмотреть более эффективный алгебраический подход.

4.Метод координат в задаче C2

1. Метод координат в пространстве — о чем, собственно, идет речь. Работать будем только с векторами. Прямые и плоскости тоже заменяются векторами, поэтому никаких проблем не возникнет.

2. Введение системы координат для многогранников. Дело в том, что в настоящей задаче C2 никаких координат не будет. Их надо вводить самостоятельно.

3. Вычисление угла между двумя прямыми. А это уже решение конкретных задач C2.

4. Вычисление угла между прямой и плоскостью. Во многих задачах C2 встречаются плоскости. Для любой прямой можно рассчитать синус угла между плоскостью и этой прямой. Именно синус — и только затем косинус!

5. Вычисление угла между двумя плоскостями. Заменяем плоскости нормальными векторами и считаем угол между последними. Косинус угла между векторами — это и косинус угла между плоскостями.

6. Дополнительные соображения — как можно упростить вычисления и грамотно их оформить. Все-таки C2 — это не B2, и здесь требуется привести полноценно решение задачи.

Четырехугольная пирамида в задаче C2

Пирамида — самый нелюбимый многогранник в задаче C2. Потому что ее координаты находятся труднее всего. И если точки основания еще как-то рассчитываются, то вершины пирамиды — настоящий ад. Сегодня мы разберемся с четырехугольной пирамидой, а в следующий раз — с треугольной.

Дополнительные соображения

Что можно сделать, когда все уже сделано? Правильно: можно попробовать упростить. А поскольку метод координат простотой и маленькими объемами вычислений не страдает, некоторая оптимизация здесь просто необходима.

Угол между двумя прямыми

Чаще всего в задаче C2 требуется найти угол именно между двумя прямыми. Иногда точки подобраны так, что вычислить угол между прямыми иначе как с помощью метода координат будет затруднительно. Во всех случаях сложность вычислений сильно зависит от того, какая фигура дается в задаче. Самый простой вариант — это куб и точки на его гранях. Чуть сложнее обстоит дело с трехгранной призмой.

Введение системы координат

В чистом виде метод координат встречается редко. Как правило, сначала требуется ввести систему координат, отыскать нужные точки — и только затем находить ответ. Для каждого многогранника в задаче C2 существует оптимальный вариант введения системы координат, который повышает наглядность самого решения и значительно сокращает общий объем вычислений.

Метод координат в пространстве

Метод координат — это только на первый взгляд сложно. Координаты, векторы, километровые вычисления... А в результате получается намного быстрее и проще, чем стандартные приемы. В задаче C2 метод координат работает на полную силу, и многие специалисты по ЕГЭ признают, что координатный подход — самый оптимальный способ нахождения ответа.

5.Примеры решения задач C2 в подготовке к ЕГЭ

Угол между двумя прямыми

Угол между двумя прямыми равен углу между их направляющими векторами. Таким образом, если вам удастся найти координаты направляющих векторов a = (x₁; y₁; z₁) и b = (x₂; y₂; z₂), то сможете найти угол. Точнее, косинус угла по формуле:

Посмотрим, как эта формула работает на конкретных примерах:

• Задача. В кубе ABCDA₁B₁C₁D₁ отмечены точки E и F — середины ребер A₁B₁ и B₁C₁ соответственно. Найдите угол между прямыми AE и BF.

Решение. Поскольку ребро куба не указано, положим AB = 1. Введем стандартную систему координат: начало в точке A, оси x, y, z направим вдоль AB, AD и AA₁ соответственно. Единичный отрезок равен AB = 1. Теперь найдем координаты направляющих векторов для наших прямых.

Найдем координаты вектора AE. Для этого нам потребуются точки A = (0; 0; 0) и E = (0,5; 0; 1). Поскольку точка E — середина отрезка A₁B₁, ее координаты равны среднему арифметическому координат концов. Заметим, что начало вектора AE совпадает с началом координат, поэтому AE = (0,5; 0; 1).

Теперь разберемся с вектором BF. Аналогично, разбираем точки B = (1; 0; 0) и F = (1; 0,5; 1), т.к. F — середина отрезка B₁C₁. Имеем:
BF = (1 − 1; 0,5 − 0; 1 − 0) = (0; 0,5; 1).

Итак, направляющие векторы готовы. Косинус угла между прямыми — это косинус угла между направляющими векторами, поэтому имеем:

Ответ: arccos 0,8

Задача. В правильной трехгранной призме ABCA₁B₁C₁, все ребра которой равны 1, отмечены точки D и E — середины ребер A₁B₁ и B₁C₁ соответственно. Найдите угол между прямыми AD и BE.

• Решение. Введем стандартную систему координат: начало координат в точке A, ось x направим вдоль AB, z — вдоль AA₁. Ось y направим так, чтобы плоскость OXY совпадала с плоскостью ABC. Единичный отрезок равен AB = 1. Найдем координаты направляющих векторов для искомых прямых.

Для начала найдем координаты вектора AD. Рассмотрим точки: A = (0; 0; 0) и D = (0,5; 0; 1), т.к. D — середина отрезка A₁B₁. Поскольку начало вектора AD совпадает с началом координат, получаем AD = (0,5; 0; 1).

Теперь найдем координаты вектора BE. Точка B = (1; 0; 0) считается легко. С точкой E — серединой отрезка C₁B₁ — чуть сложнее. Имеем:

Осталось найти косинус угла:

Ответ: arccos 0,7

• Задача. В правильной шестигранной призме ABCDEFA₁B₁C₁D₁E₁F₁, все ребра которой равны 1, отмечены точки K и L — середины ребер A₁B₁ и B₁C₁ соответственно. Найдите угол между прямыми AK и BL.

Решение. Введем стандартную для призмы систему координат: начало координат поместим в центр нижнего основания, ось x направим вдоль FC, ось y — через середины отрезков AB и DE, а ось z — вертикально вверх. Единичный отрезок снова равен AB = 1. Выпишем координаты интересующих нас точек:

Точки K и L — середины отрезков A₁B₁ и B₁C₁ соответственно, поэтому их координаты находятся через среднее арифметическое. Зная точки, найдем координаты направляющих векторов AK и BL:

Теперь найдем косинус угла:

Ответ: arccos 0,9

• Задача. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, отмечены точки E и F — середины сторон SB и SC соответственно. Найдите угол между прямыми AE и BF.

Решение. Введем стандартную систему координат: начало в точке A, оси x и y направим вдоль AB и AD соответственно, а ось z направим вертикально вверх. Единичный отрезок равен AB = 1.

Точки E и F — середины отрезков SB и SC соответственно, поэтому их координаты находятся как среднее арифметическое концов. Выпишем координаты интересующих нас точек:
A = (0; 0; 0); B = (1; 0; 0)

Зная точки, найдем координаты направляющих векторов AE и BF:

Координаты вектора AE совпадают с координатами точки E, поскольку точка A — начало координат. Осталось найти косинус угла:

Четырехугольная пирамида в задаче C2

Решая задачу C2 методом координат, многие ученики сталкиваются с одной и той же проблемой. Они не могут рассчитать координаты точек, входящих в формулу скалярного произведения. Наибольшие трудности вызывают пирамиды. И если точки основания считаются более-менее нормально, то вершины — настоящий ад.

Есть еще треугольная пирамида (она же — тетраэдр).

Для начала вспомним определение:

Определение

Правильная пирамида — это такая пирамида, у которой:

1. В основании лежит правильный многоугольник: треугольник, квадрат и т.д.;

2. Высота, проведенная к основанию, проходит через его центр.

В частности, основанием четырехугольной пирамиды является квадрат. Прямо как у Хеопса, только чуть поменьше.

Ниже приведены расчеты для пирамиды, у которой все ребра равны 1. Если в вашей задаче это не так, выкладки не меняются — просто числа будут другими.

Заключение

ЕГЭ – уже не новая форма проверки знаний ученика. Проверяя эти знания, мы довольно часто приходим к неутешительным результатам. Эти результаты не радуют чаще всего не только учителя, но и самого ученика. И это бывает потому, что ученик не владеет знаниями даже на базовом уровне.

Значит учить и научить так, чтобы, по возможности, каждый получил “зачет” на экзамене, мы должны всех, кто пришел учиться в зависимости от уровня их знаний и способностей, а также потребностей каждого отдельно взятого ученика.

Задача учителя – научить всех сидящих перед ним учеников с учетом их возможностей и способностей. Это очень трудная и ответственная работа для каждого учителя, работающего в выпускном классе.

Список литературы

1. Единственные реальные варианты заданий для подготовки к единому государственному экзамену. ЕГЭ – 2007, 2008. Математика/ А.Г.Клово. – М.: Федеральный центр тестирования, 2007, 2008.

2. Математика. Подготовка к ЕГЭ – 2008. Вступительные испытания. Под редакцией Ф.Ф. Лысенко. – Ростов-на Дону: Легион, 2007.

3. В.В. Кочагин, М.Н.Кочагина. Тестовые задания к основным учебникам. Рабочая тетрадь. 9 класс. – М. Эксмо, 2008.

4. Алгебра и начала анализа: учеб. Для 10 кл. общеобразоват.учреждений: базовый и профил. уровни (С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин). – 6-е изд. – М.: Просвещение, 2007.

5. Алгебра и начала анализа: учеб. Для 11 кл. общеобразоват.учреждений: базовый и профил. уровни (С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин). – 6-е изд. – М.: Просвещение, 2007.

6. Математика. ЕГЭ – 2008. Тематические тесты. Часть I (А 1 – А10, В 1 – 3). Под редакцией Ф.Ф. Лысенко. – Ростов-на-Дону: Легион, 2008.

7. Математика. ЕГЭ – 2008. Тематические тесты. Часть II (В 4 – 11, С 1, С 2). Под редакцией Ф.Ф. Лысенко. – Ростов-на-Дону: Легион, 2008.

12