Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Решение задач с помощью систем уравнений
Тип урока: практикум по решению задач.
Оборудование: тетради, учебники, компьютеры, карточки для выполнения групповой и индивидуальной работы.
Цель: научить решать задачи с помощью систем уравнений
Задачи:
• образовательная: продолжить формирование навыков сознательного выбора способа решения системы;
• развивающая: развивать потребность в нахождении рациональных способов решения;
• воспитательная:
• способствовать воспитанию чувства ответственности за совместную деятельность;
• способствовать воспитанию целеустремленности и настойчивости; умения преодолевать трудности, делать осознанный выбор;
• способствовать развитию любознательности и творческой активности
Планируемый результат:
Знать:
• способы решения систем линейных уравнений;
• алгоритм решения задач.
Уметь:
• применять удобный способ решения систем линейных уравнений;
• применять алгоритм решения задач на практике;
• использовать различные источники знаний;
• работать с карточками различного содержания;
• работать в группах, индивидуально.
Используемые технологии: уровневой дифференциации, индивидуального обучения, проблемно поисковой, групповые, ИКТ.
Методы работы:
а) методы организации учебно-познавательной деятельности: словесный, наглядный, практический, самостоятельная работа, работа под куроводством.
б) методы контроля и самоконтроля: устный опрос, фронтальный опрос, письменный контроль.1. этап. Постановка целей и задач урока
-Здравствуйте. Я рада видеть вас на уроке. Посмотрите друг на друга, улыбнитесь, и с хорошим настроением начнем урок. Всем желаю хорошей работы и успеха.
На протяжении нескольких уроков мы с вами рассматривали понятие, которое необходимо для нас.
Ответьте на вопрос, что объединяет данные высказывания? (слайд №1).
Что означает слово система?
Где еще встречается данное слово?
Ответьте на вопросы:
-Что называется решением системы уравнений?
-Что значит решить систему уравнений?
-Перечислите методы решения систем уравнений?
Чтобы узнать тему нашего урока я предлагаю решить следующие ребусы и соединить полученные слова в единое целое и назвать тему нашего урока.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Решение задач с помощью систем уравнений »
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1690 руб.
2820 руб.
1720 руб.
2860 руб.
1730 руб.
2880 руб.
1340 руб.
2240 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства




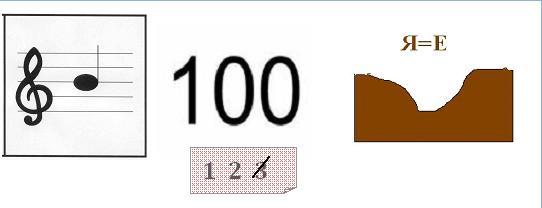
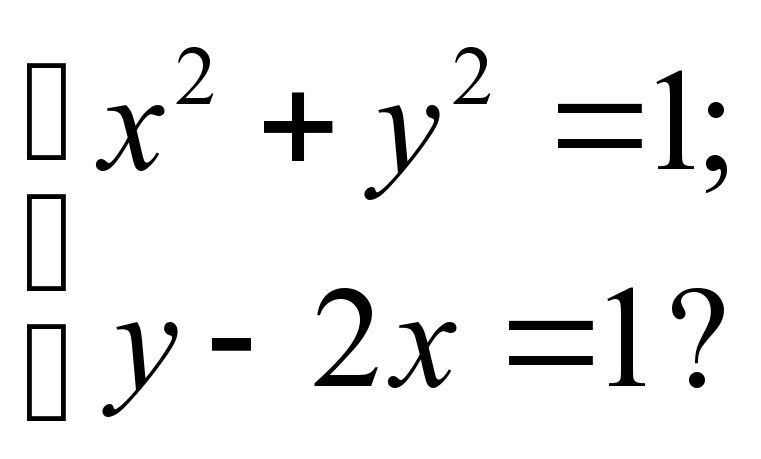
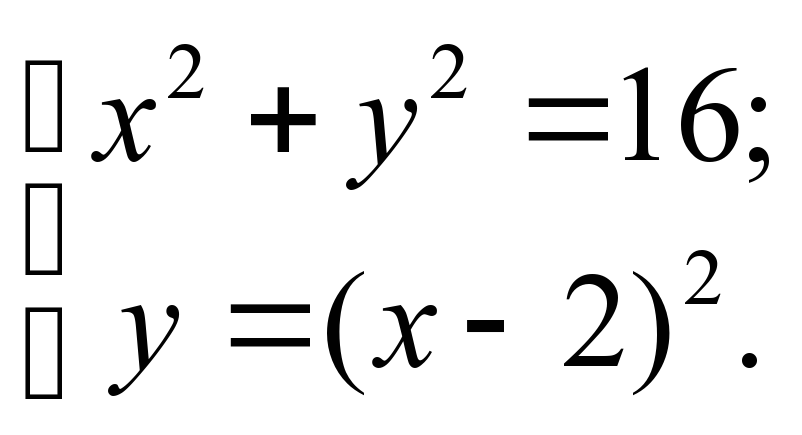
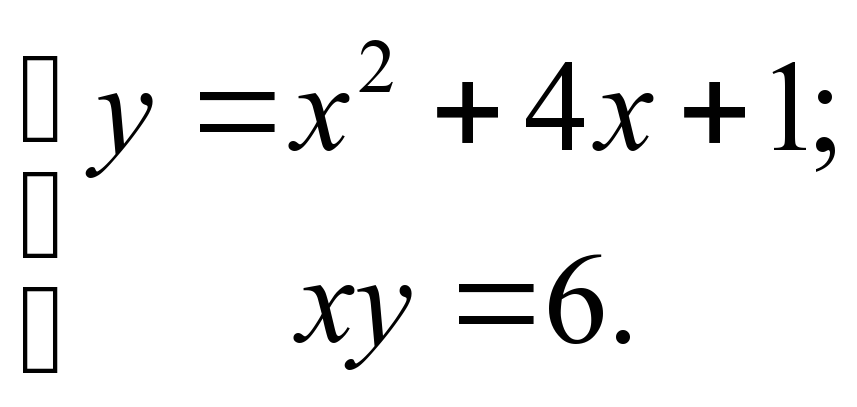
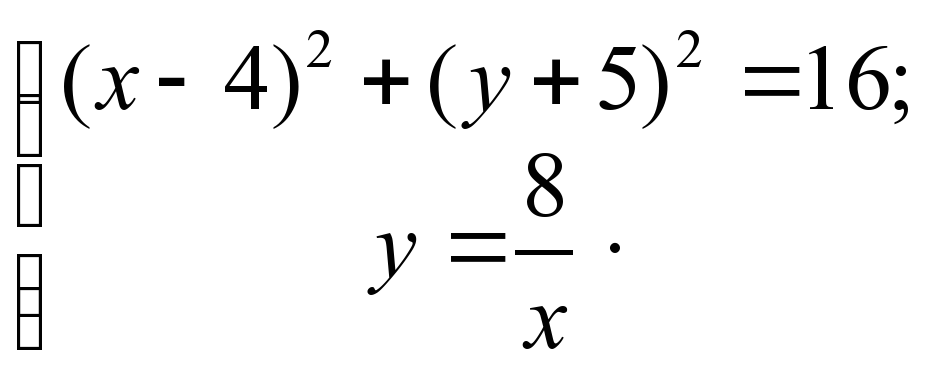
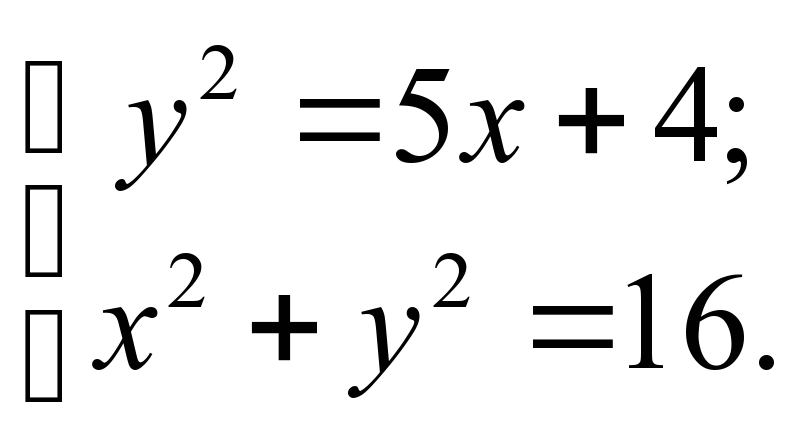
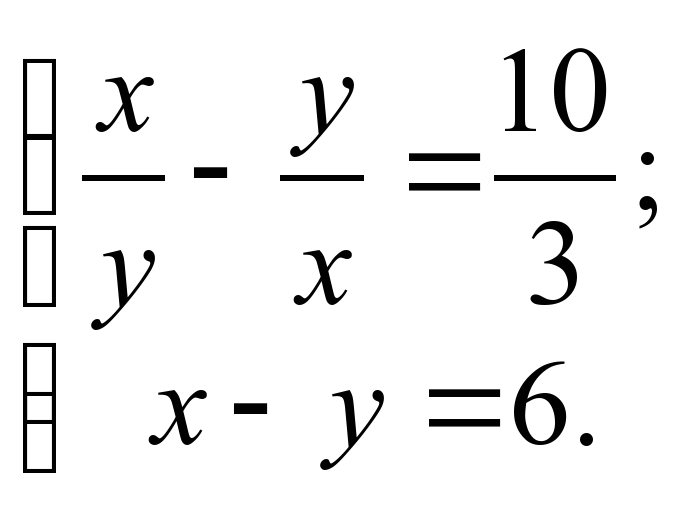





 + У =35,
+ У =35, Рифовый узел
Рифовый узел 

 2 отряд
2 отряд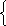 х-4у=4,8 ,
х-4у=4,8 ,

















