| Актуализация знаний 5–7 минут | 1) Из дробей 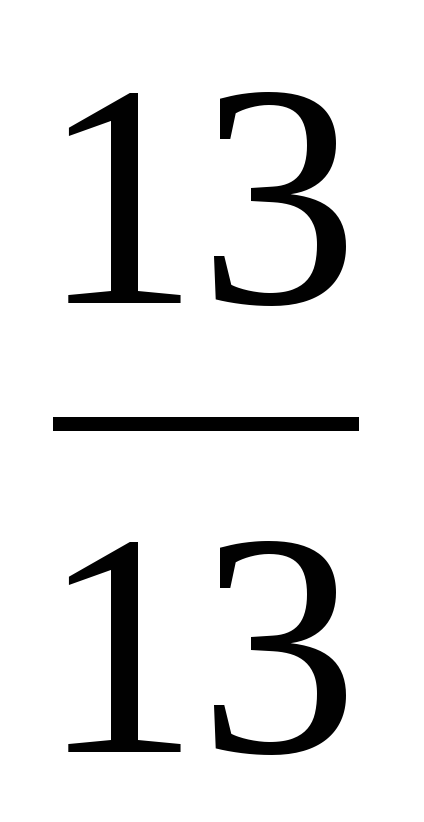 , , 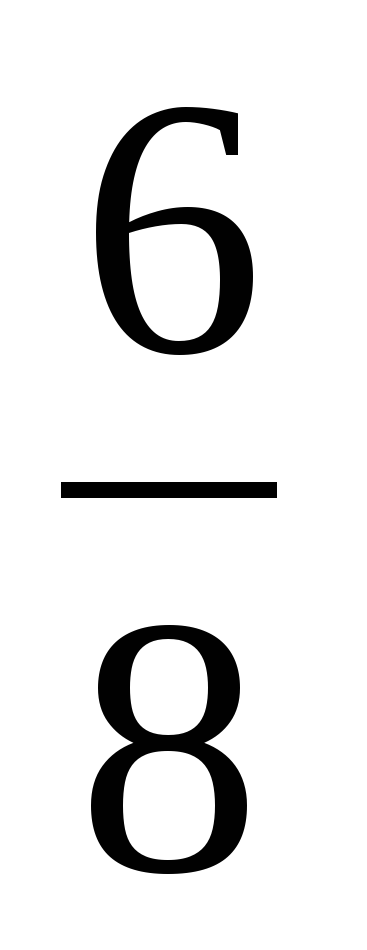 , , 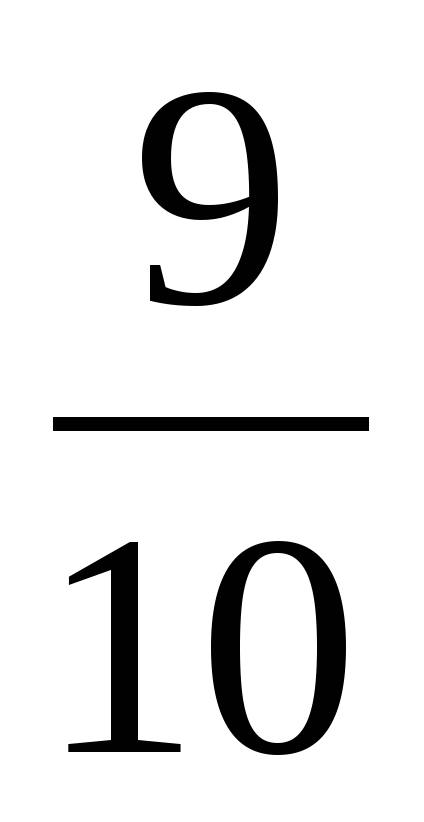 , , 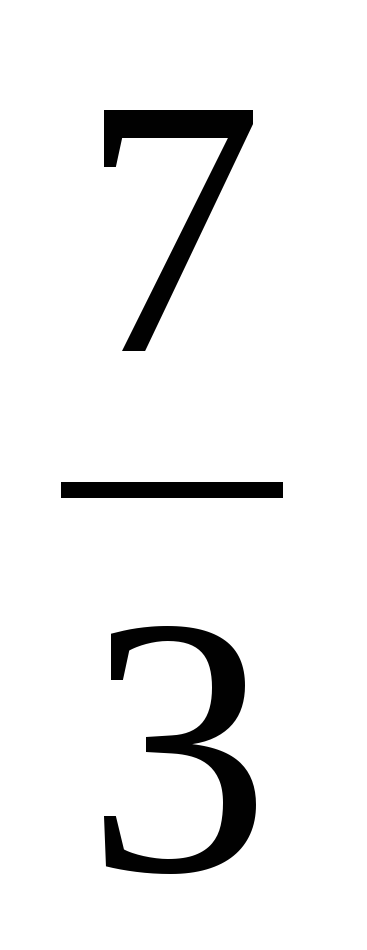 выберите правильные дроби и неправильные дроби. выберите правильные дроби и неправильные дроби. 2) Сократите дробь 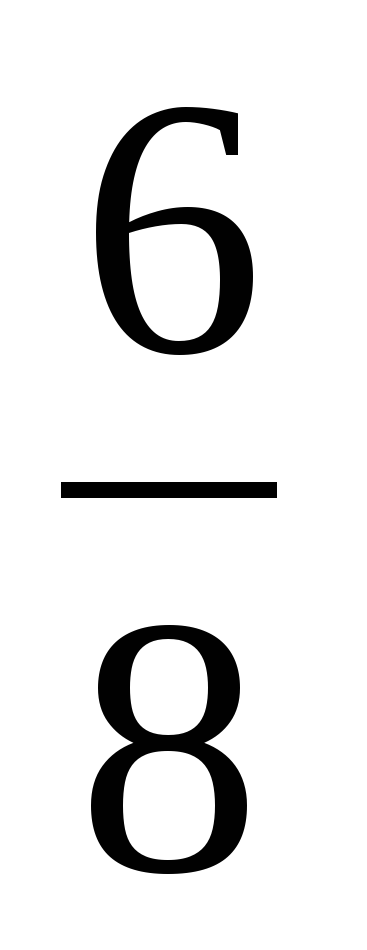 . . 3) Выделите целую часть из неправильных дробей. 4) Какая часть фигуры закрашена? Ответ дайте двумя способами – в виде смешанного числа и в виде неправильной дроби.
В ходе устной работы актуализируются умения учащихся сокращать дроби, выделять целую часть из неправильной дроби, повторяют понятия обыкновенной дроби и смешанного числа. | Ученики отвечают: 1)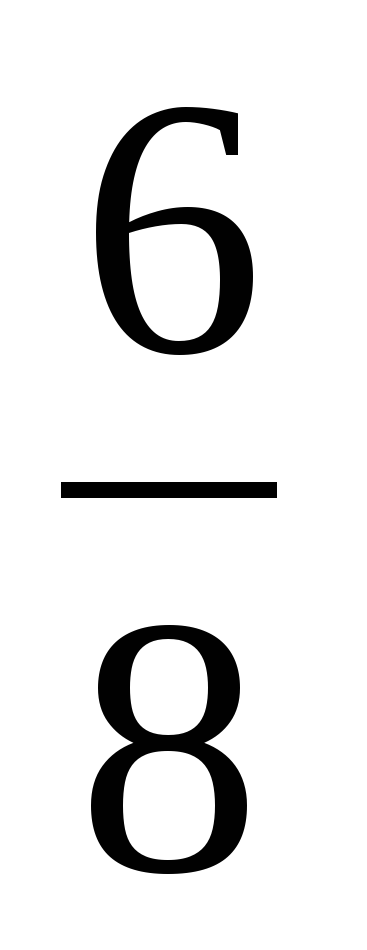 , , 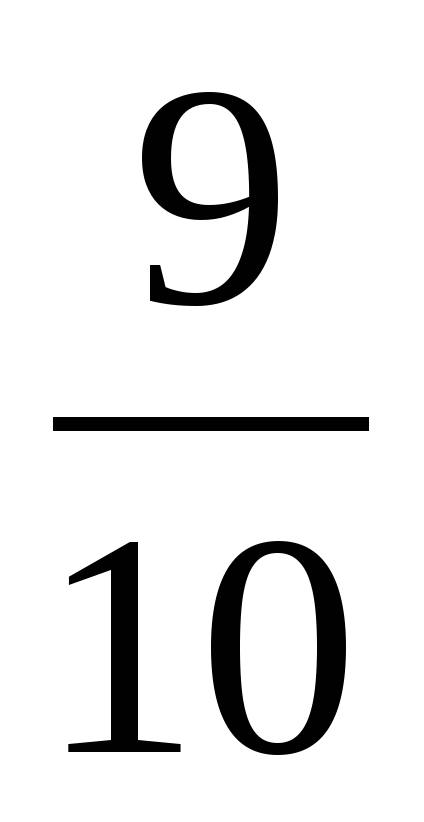 – правильные – правильные 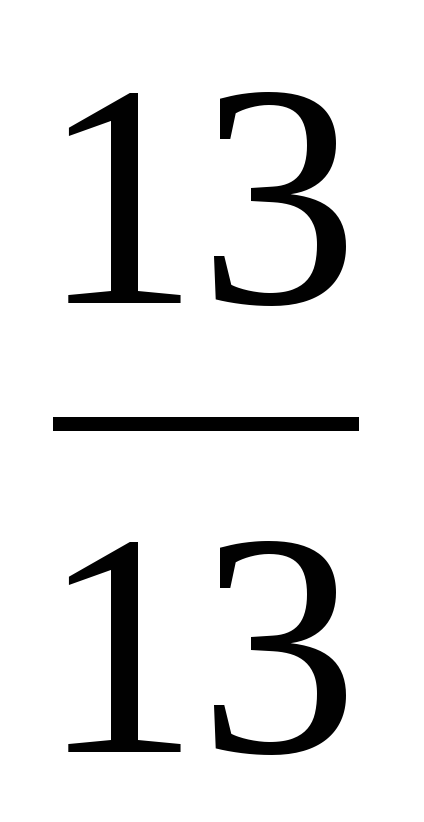 , , 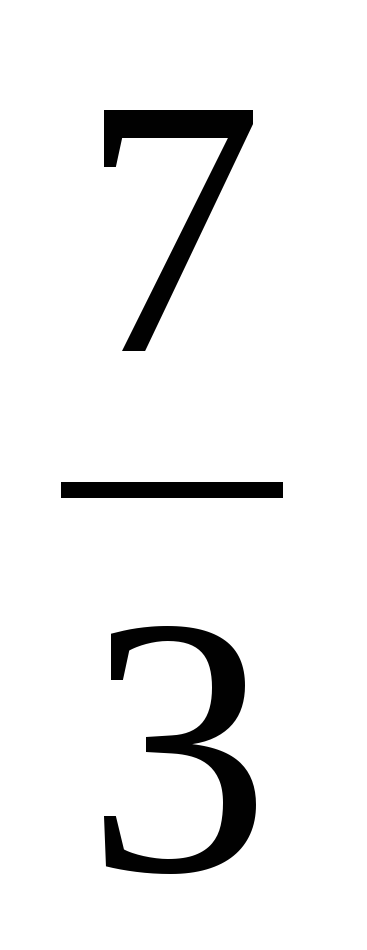 – неправильные – неправильные 2) 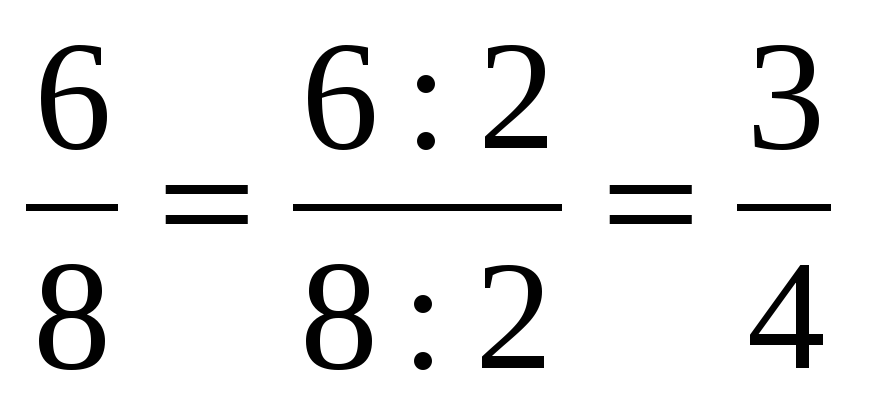 3) 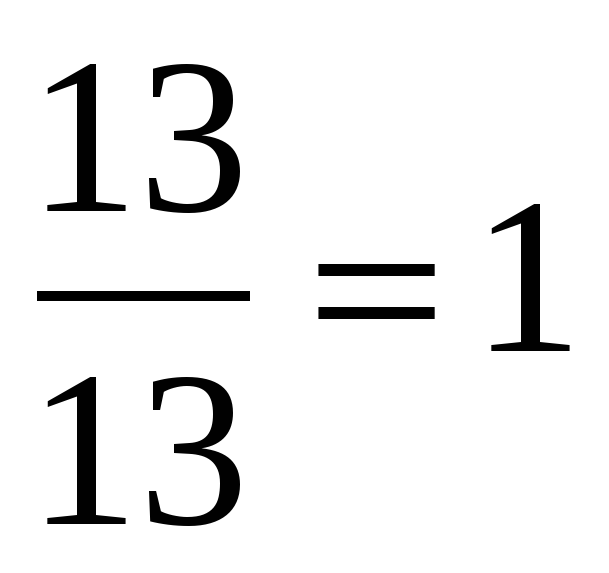 , , 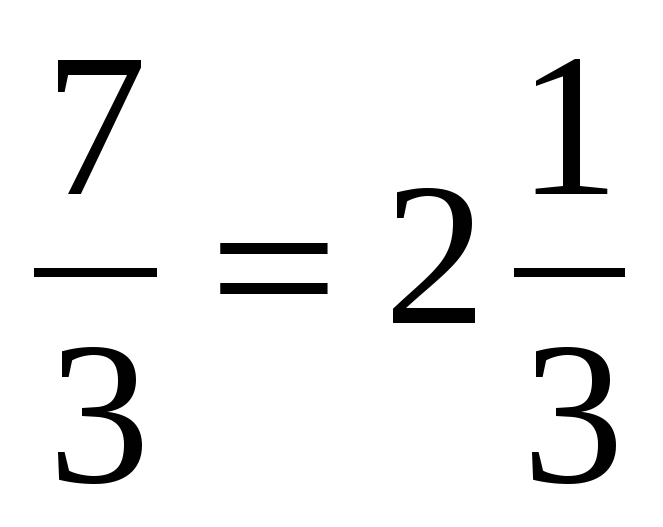 4) 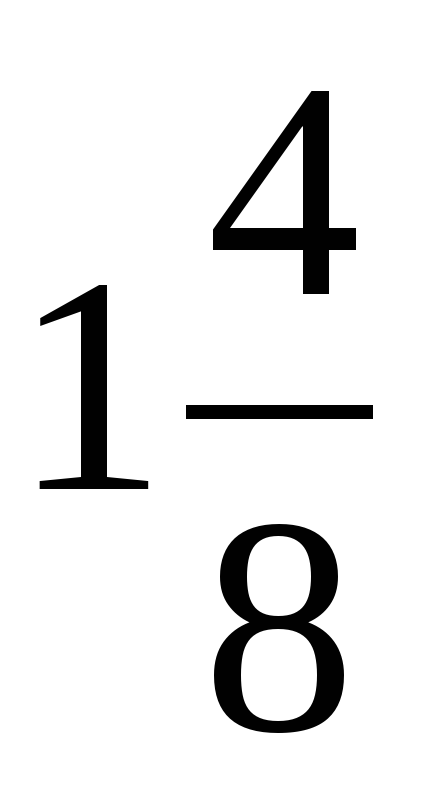 или или 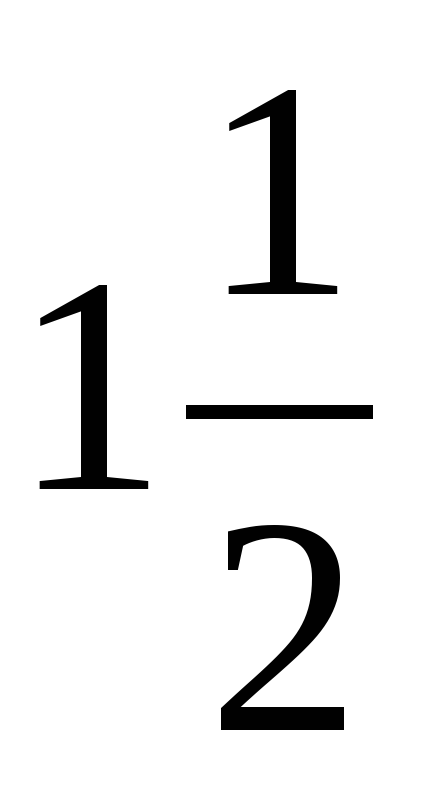 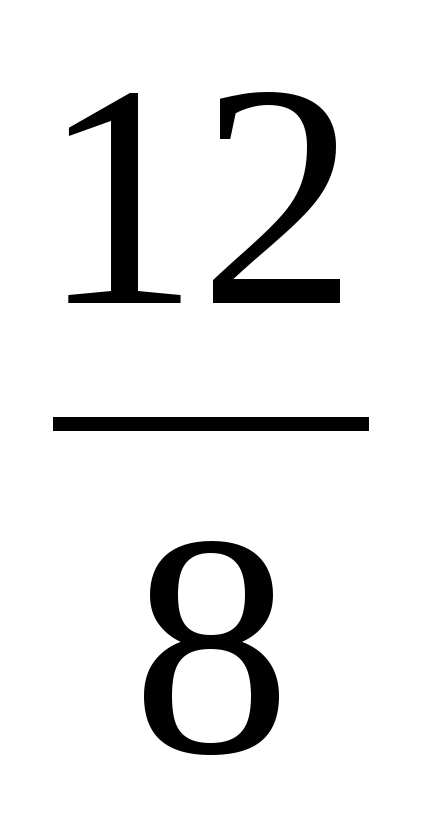 или или 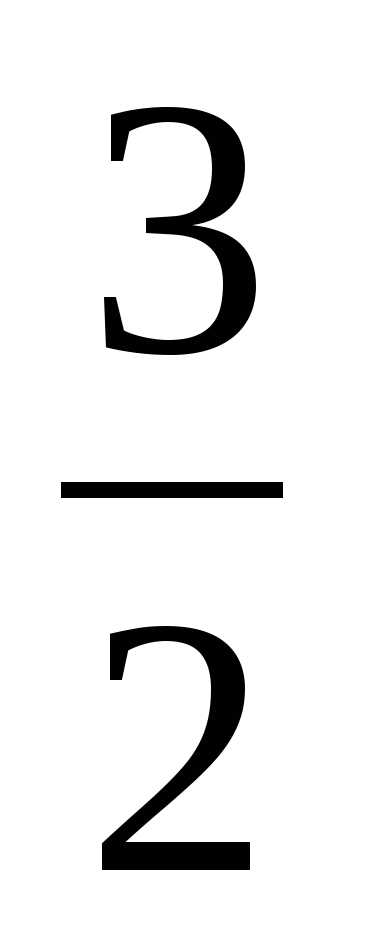 | В левом углу доски: 1) 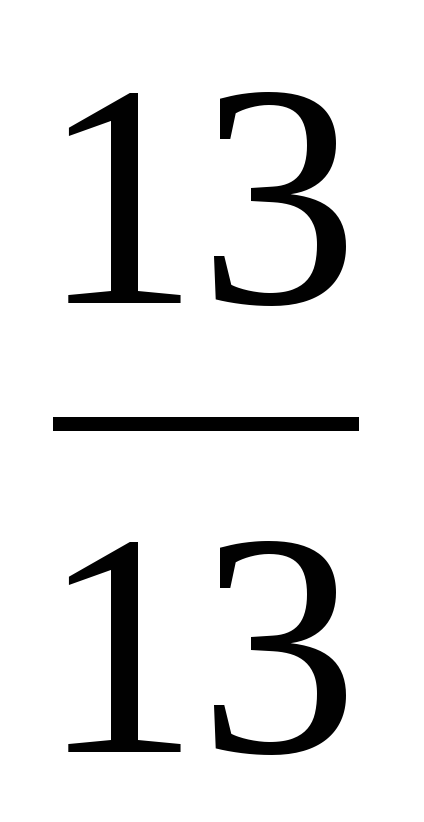 , , 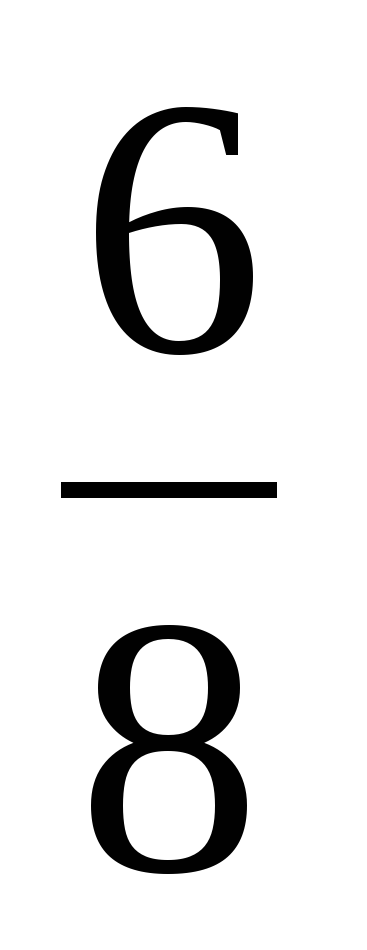 , , 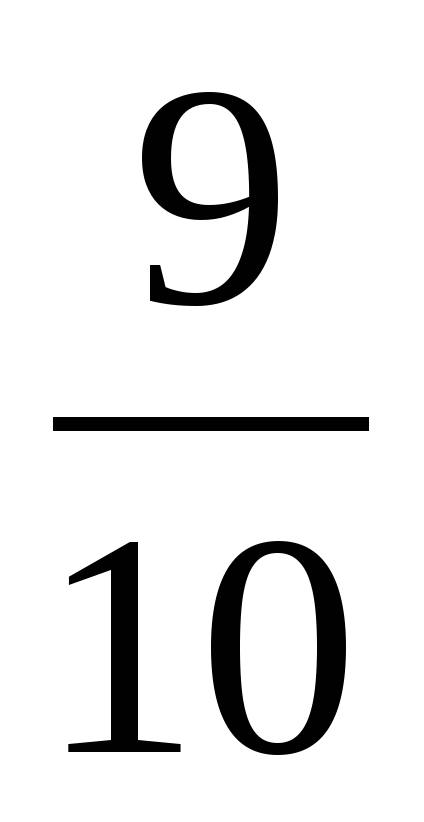 , , 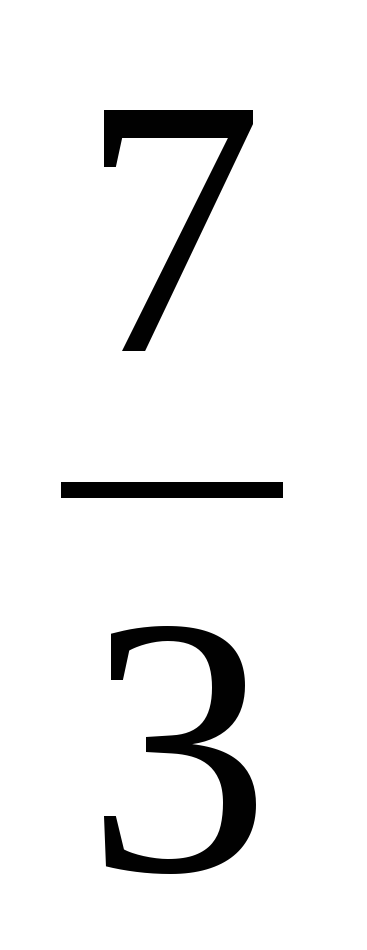 2)
| Коммуникативные (отстаивают свою точку зрения, аргументируя её) |
| Создание проблемной ситуации 3–5 минут | —Вот вам еще одно задание – выполните действия: 1) 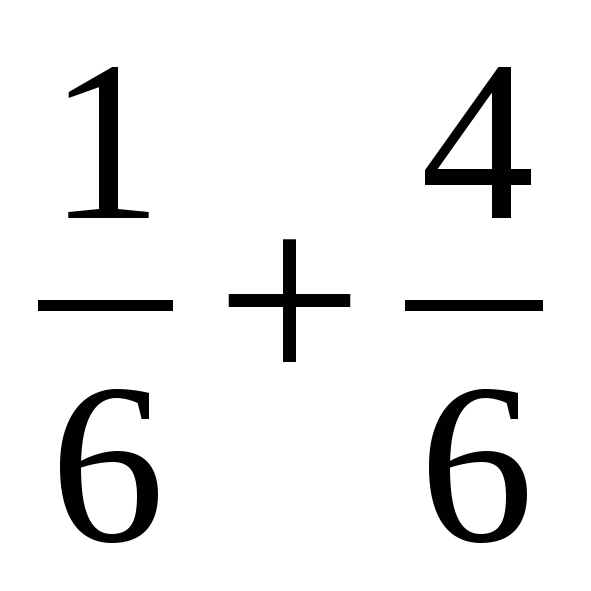 3) 3) 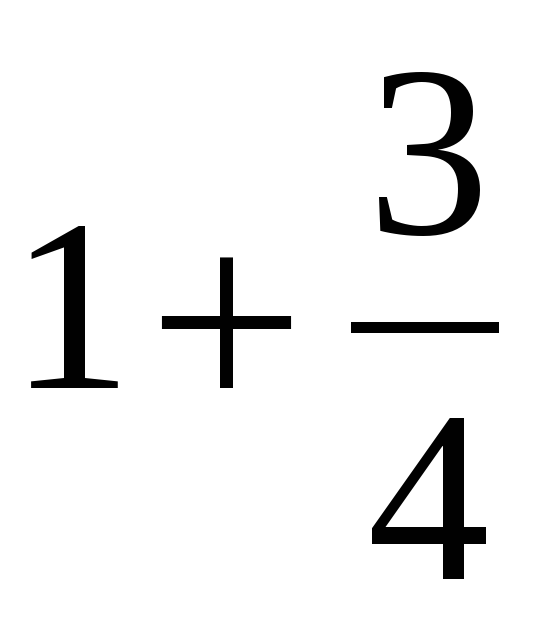 2) 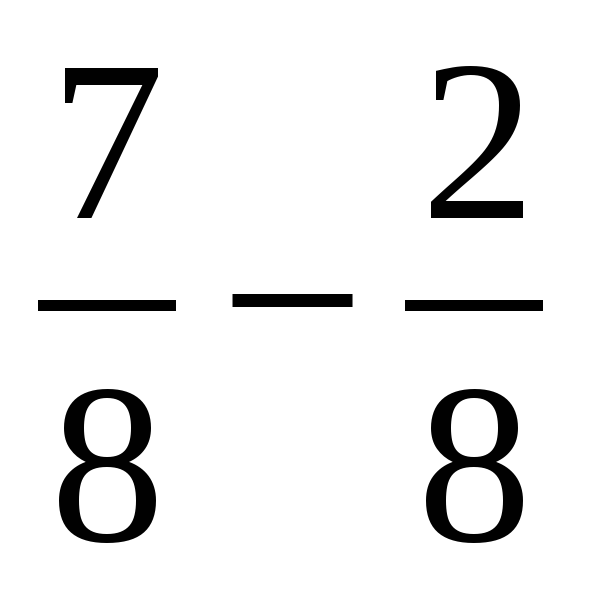 4) 4) 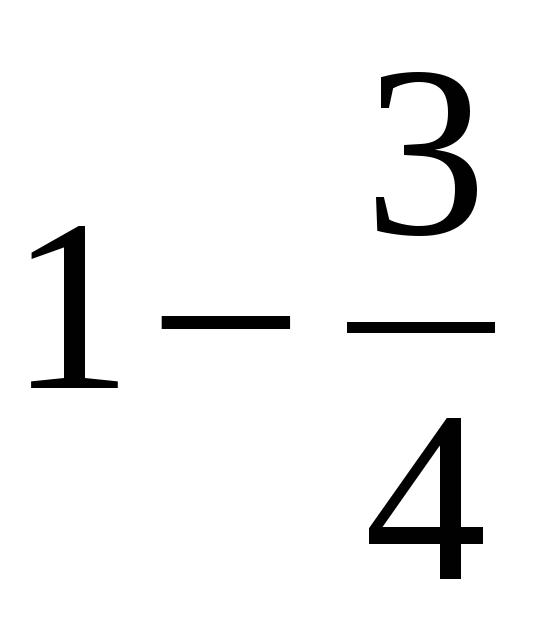 —Ребята, почему получилось столько вариантов ответов? —А какие из этих ответов правильные? | —Предполагаемые ответы: 1) 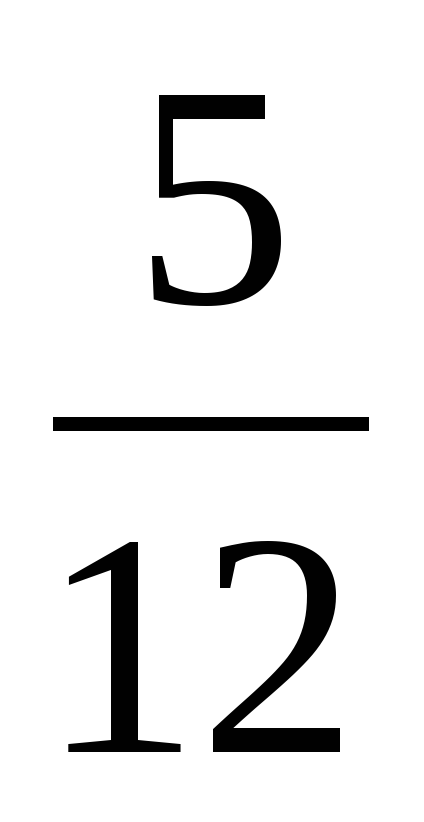 или или 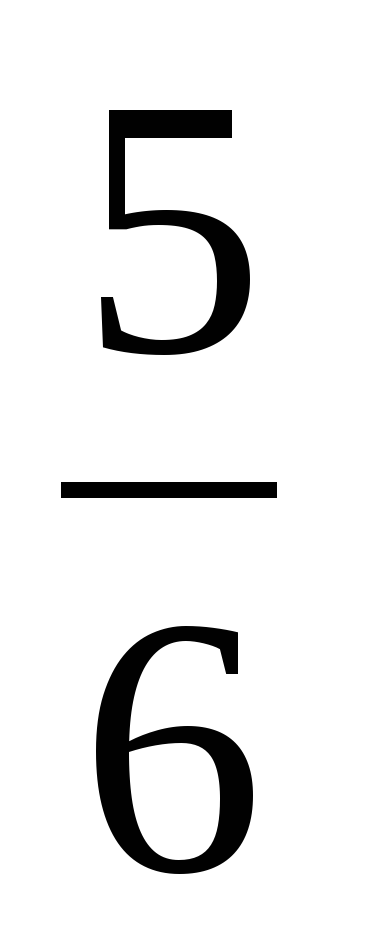 2) 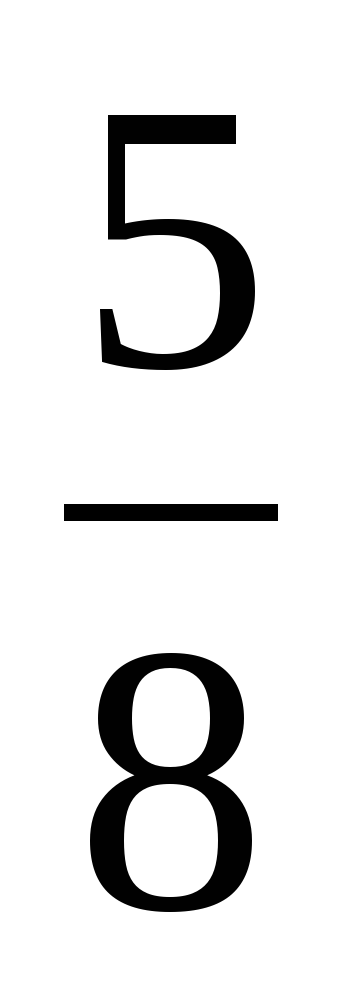 или или 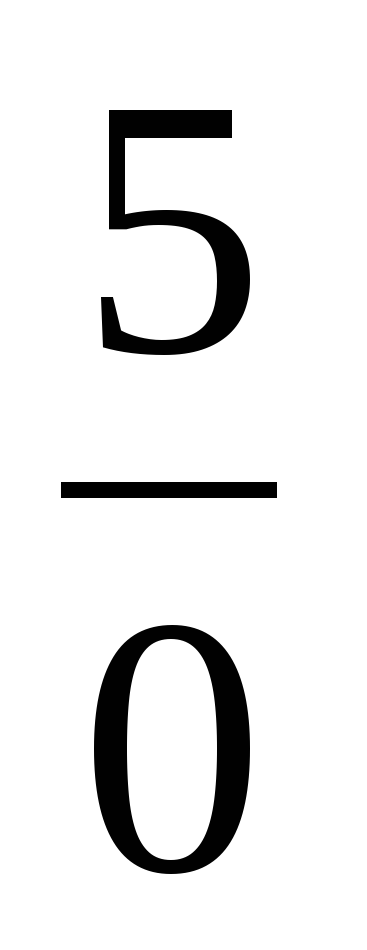 3) 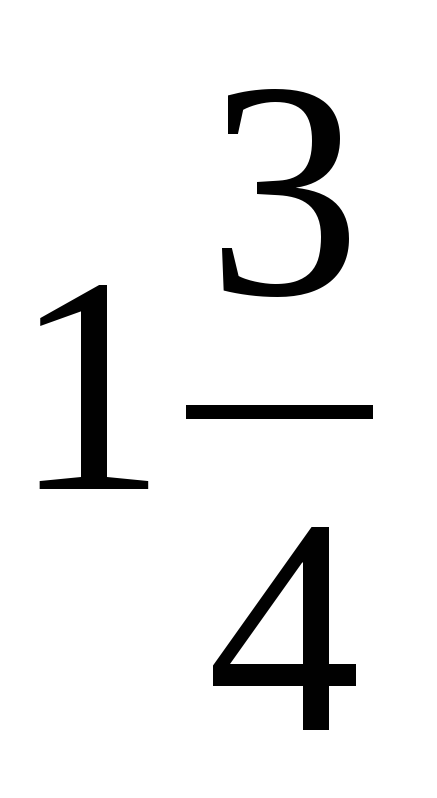 4) =? 4) =? —Потому что не умеем складывать и вычитать дроби. —Мы не знаем какие ответы правильные. | В центре доски: 1) 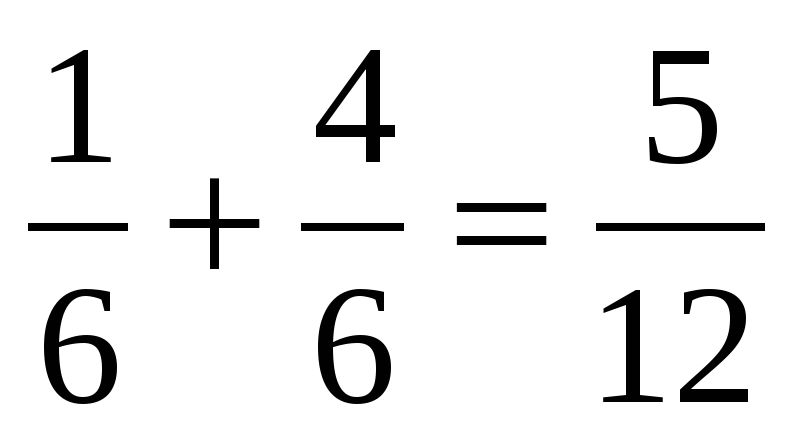 или или 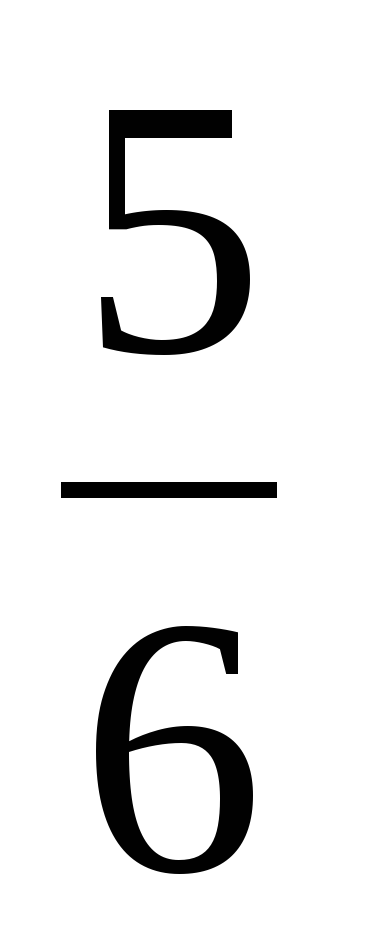 2) 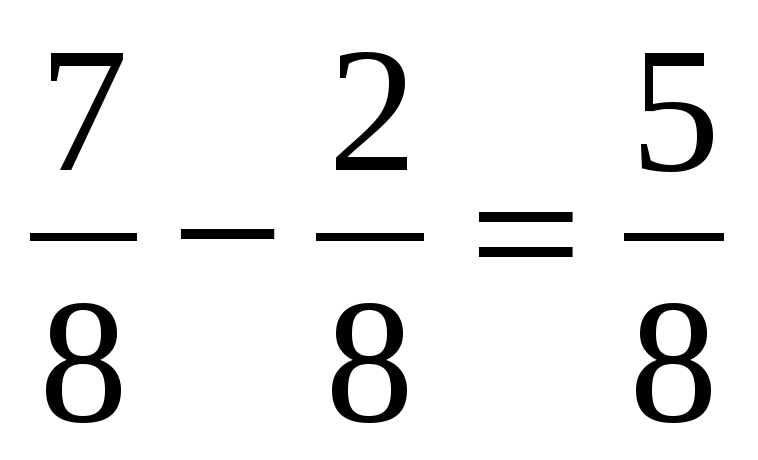 или или 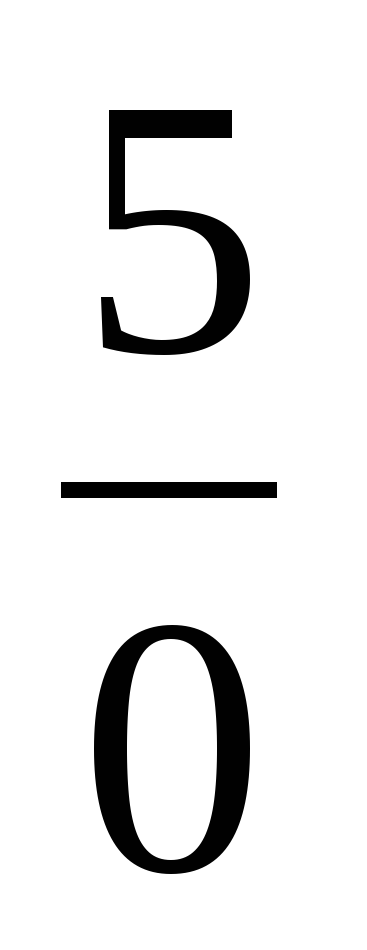 3) 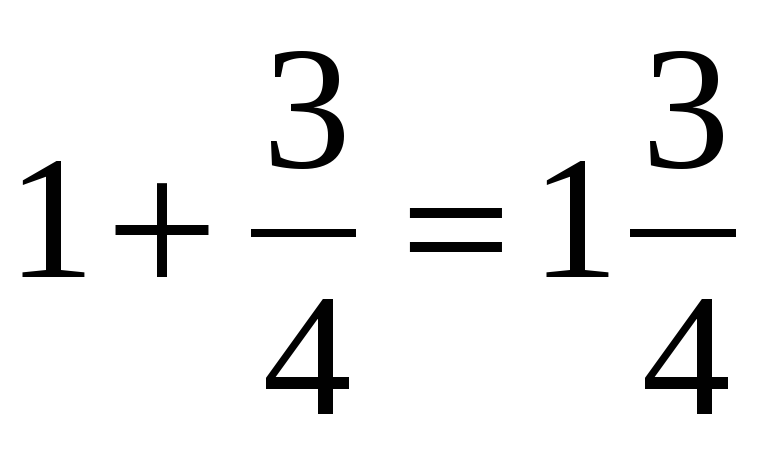 4) 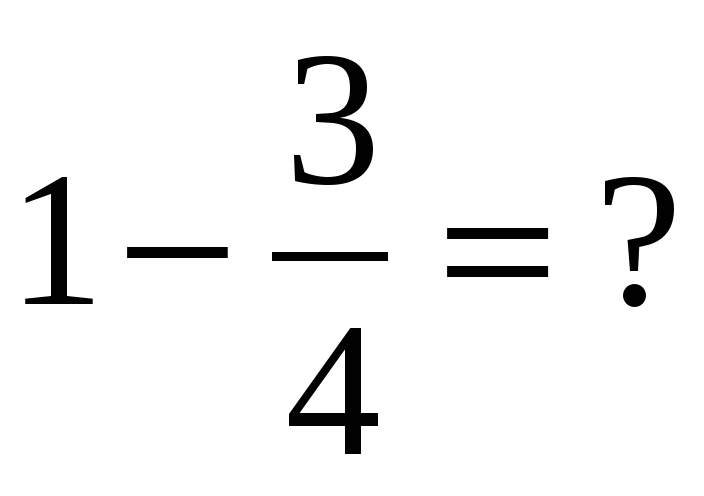 | Коммуникативные: 1) оформляют свои мысли в устной речи; 2) слушают других, пытаются принимать другую точку зрения, быть готовым изменить её
|
| Формулирование проблемы (темы и целей урока) 1–2 минуты | —Следовательно, чему сегодня надо научиться? —Как называются такие дроби?
—А какие знаменатели у дробей в данных примерах? —Тогда какова тема нашего урока?
—Запишем тему урока в тетрадях и на доске. | —Сегодня надо научиться складывать и вычитать дроби. —Такие дроби называются обыкновенными. —Знаменатели у дробей одинаковые.
—Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями. | Классная работа. Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями. | Регулятивные (обнаруживают и формулируют учебную проблему) |
| Открытие нового знания 3–5 минут | —Рассмотрите фигуру и ответьте на вопрос – какая часть фигуры закрашена: а) зеленым цветом; б) желтым цветом; в) зеленым и желтым вместе?
—Какую математическую модель можно составить для последней ситуации? —Был ли у нас такой пример в устной работе?
—Так мы теперь можем выбрать правильный ответ? —А как без рисунка выполнить сложение таких дробей?
—Рассмотрите еще одну фигуру и ответьте на вопрос – какая часть фигуры не закрашена? —Какую математическую модель можно составить для данной ситуации?
—А такой пример в устной работе был?
—И какой же правильный ответ?
—А как без рисунка выполнить вычитание дробей? —Тогда какой ответ правильный в примере №2? | —Закрашена: а) 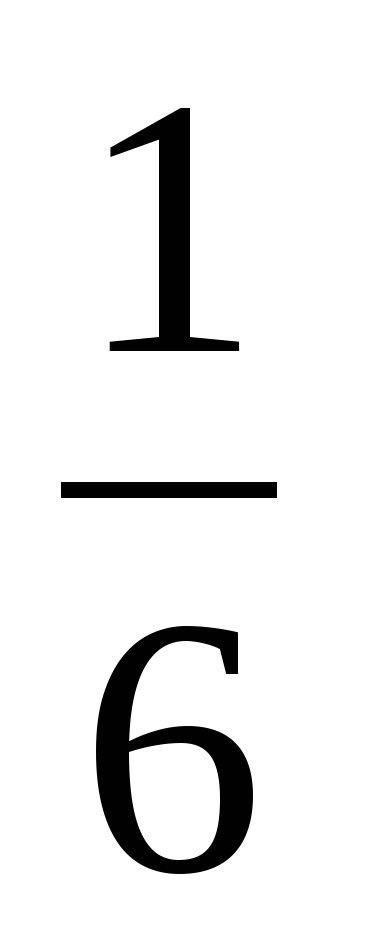 часть фигуры; часть фигуры; б) 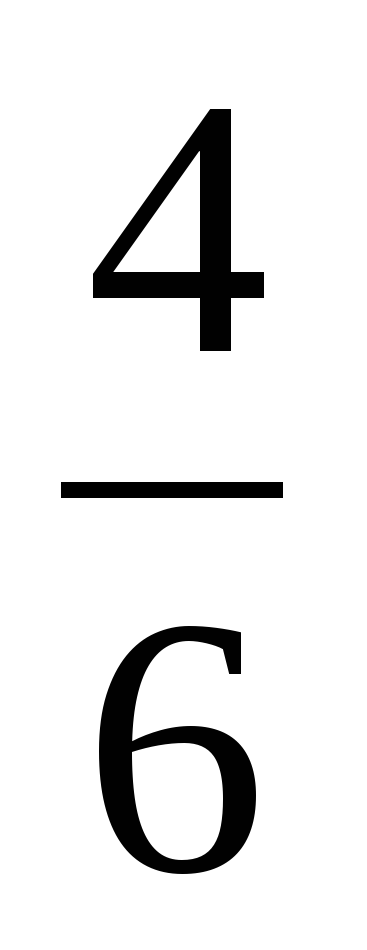 ; в) ; в) 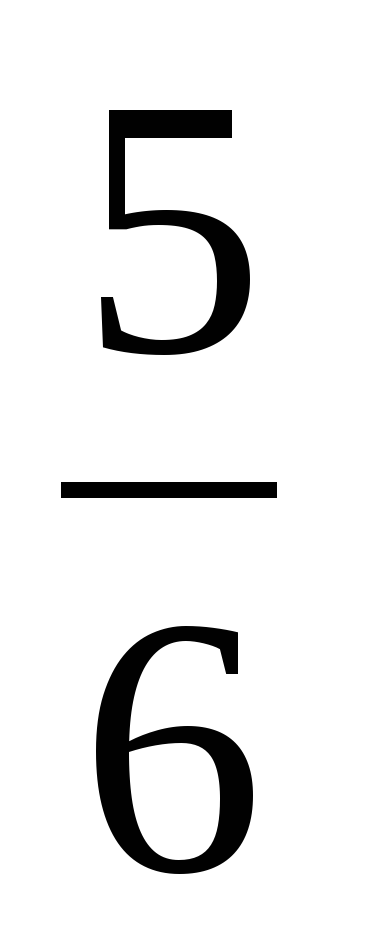 . .
—Модель такая: 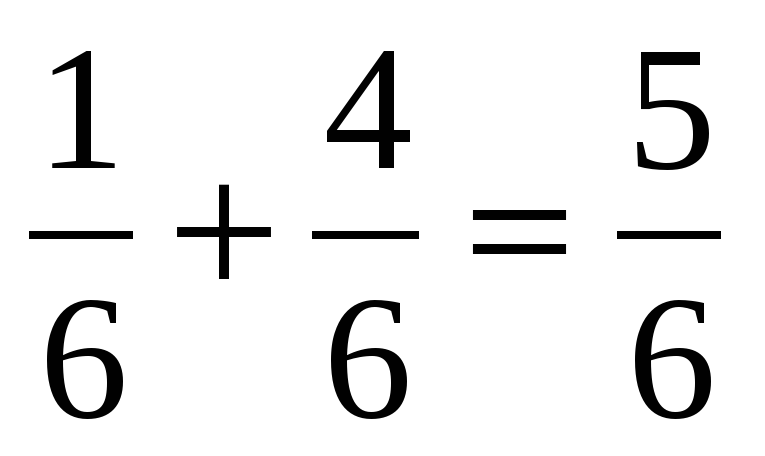
—Да, был. Это первый пример. —Да, это 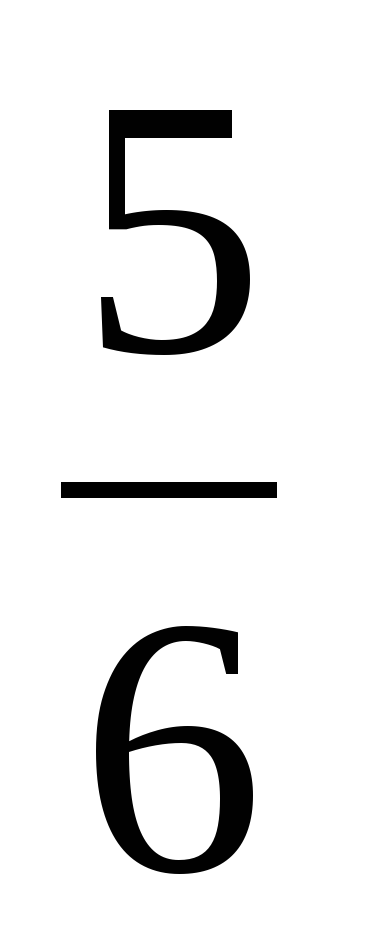 . . —Надо сложить числители, а знаменатель оставить без изменения.
—Закрашена 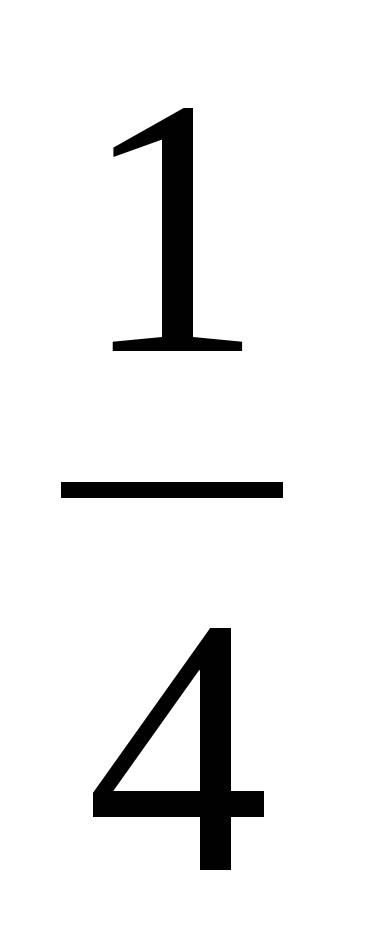 фигуры. фигуры.
—Модель такая: 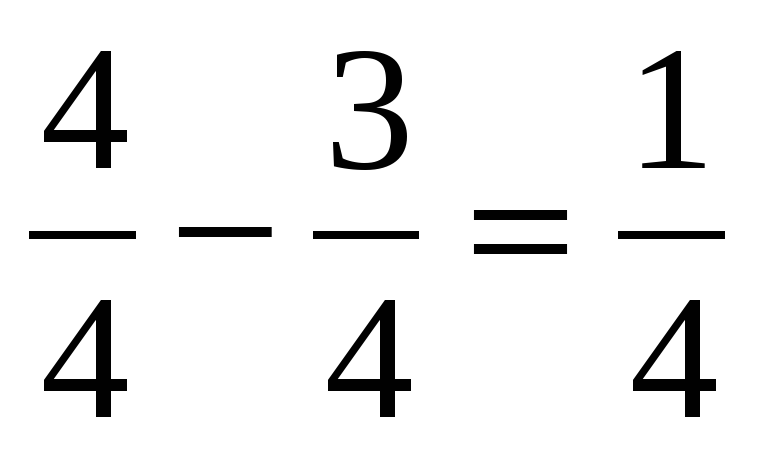
—Да, это четвертый пример. —Ответ выбираем 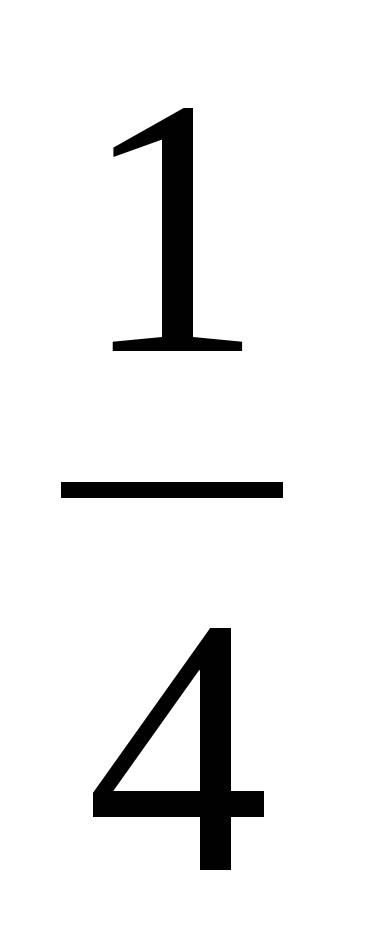 . . —Надо вычесть числители, а знаменатель не менять. —Получится 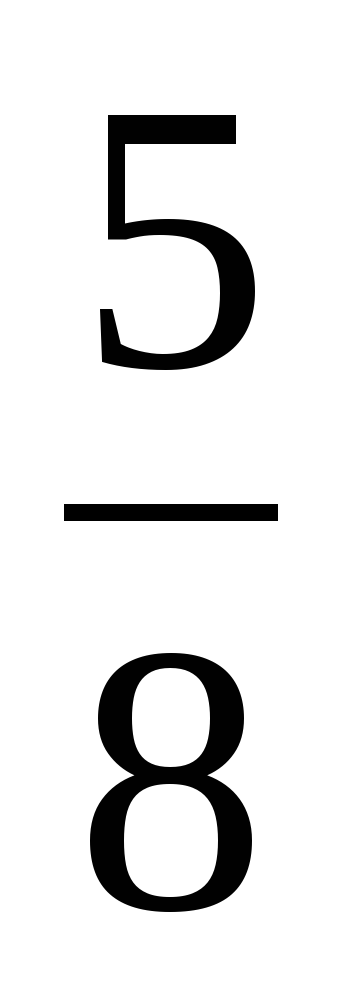 . . | В левом углу доски:
По ходу урока появляется: 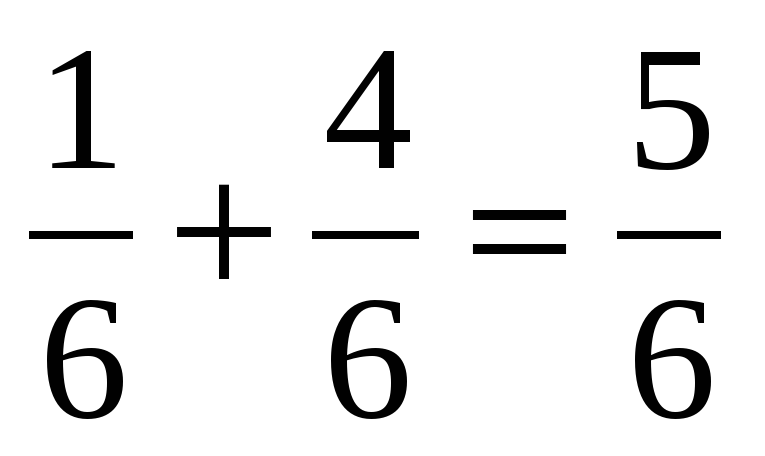
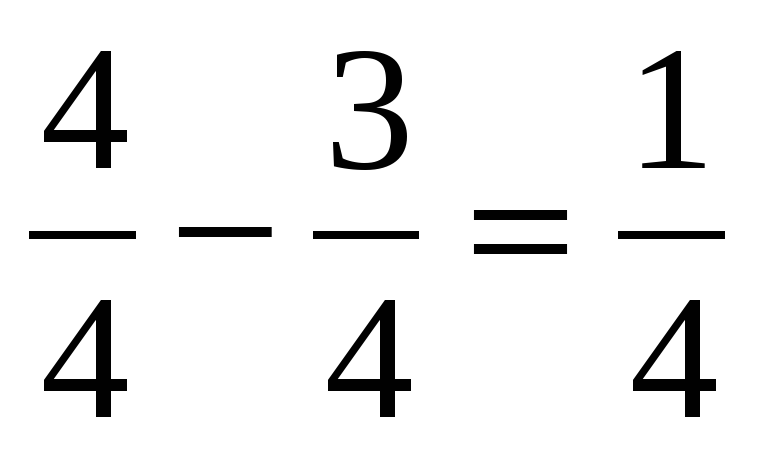
| Познавательные (выполняют сравнение, анализ) |
| Формулирование нового знания 1–2 минуты | —Где можно посмотреть точную формулировку правил? —Правильно. Тогда откройте учебник, найдите правила и назовите страницу. Прочитаем эти правила. —Перепишите правила в тетрадь, а затем в паре проговорите их друг другу. | —В учебнике.
—На странице 118. (Один ученик читает правила вслух.) —Записывают в тетрадях и проговаривают в паре: Чтобы сложить (вычесть) дроби с одинаковыми знаменателями, надо сложить (вычесть) их числители, а знаменатель оставить без изменения. | На центральной доске появляется образец решения: 1) 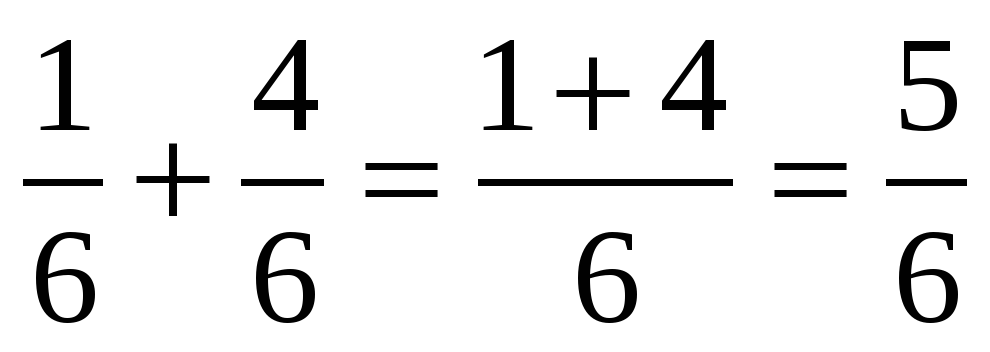 2) 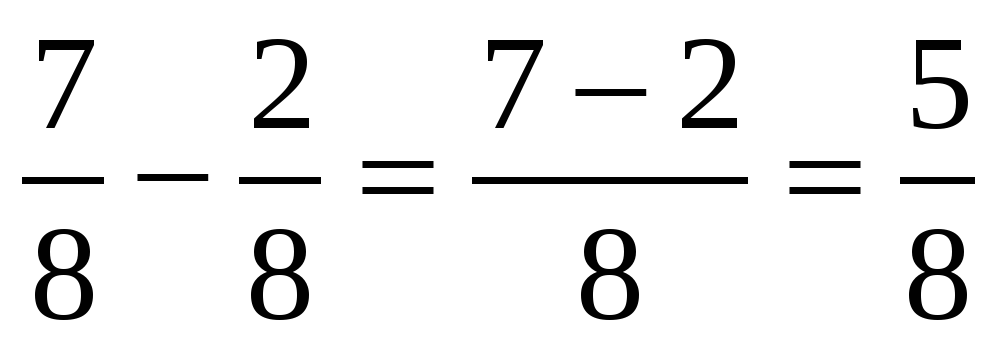
| Коммуникативные (читают вслух и про себя текст учебника)
|
| Первичное применение нового знания 2–3 минуты | —Применим новые правила при выполнении заданий в учебнике: № 422 (а, б) № 423 (а, в) + № 424 для тех, кто работает вперед. | —Два ученика по очереди выполняют у доски (по два примера): № 422 (а, б) а) 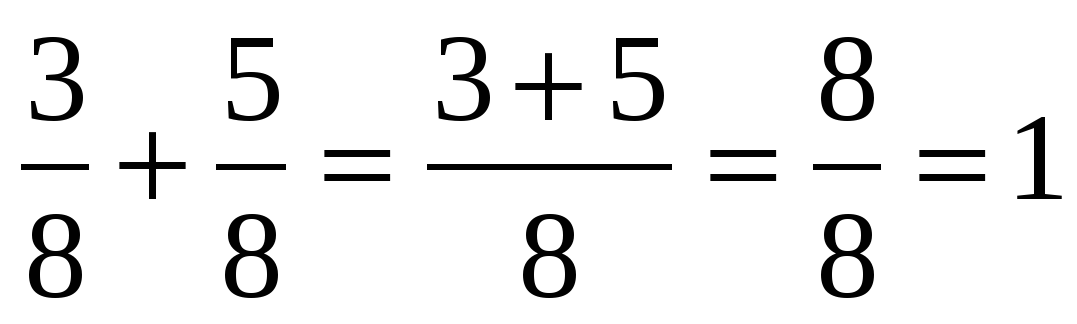 б) № 423 (а, в) а) в) | Критерии самооценки (для учеников, работающих у доски): -самостоятельность выполнения; -наличие комментариев по ходу решения; -была ли помощь учителя или учеников по ходу решения; -были ли ошибки в решении.
Остальным ученикам дается задание учителем – найти ошибки в решении ученика у доски. | Регулятивные (определяют степень успешности своей работы) |
| Самостоятельная работа 3–5 минут | —А теперь проверим, как вы усвоили новые правила. В самостоятельной работе два задания. —Разработаем критерии оценивания работы: -выполнили сложение по правилу (1 балл); -выполнили вычитание по правилу (1 балл); -сократил дробь (1 балл); -выделил целую часть (1 балл). Итого: максимум 4 балла – оценка «5», 3 балла – оценка «4», 2 балла – оценка «3», 0-1 балл – оценка «2». —Приступаем к проверке. На доске написан правильный вариант решения. Оцените свою работу по данным критериям. | Ученики выполняют примеры по вариантам: В-1 1) 2)
В-2 1) 2) | На обратной стороне доски образец выполнения. В-1 1) 2)
В-2 1) 2) | Регулятивные (планирование, самооценивание) |
| Рефлексия. Итог урока 1–2 минуты | —Урок подходит к концу. Давайте посмотрим, а мы цели достигли? В начале урока вам были выданы оценочные листы. По следующим критериям оцените свою работу на уроке. —Подпишите и сдайте оценочные листы.
По желанию учащихся учитель выставляет эти оценки в журнал. | —Работают с оценочным листом, выставляют себе оценки за урок. Перевод баллов в оценку: 10 баллов и больше – оценка «5»; 8-9 баллов – оценка «4»; 6-7 баллов – оценка «3»; 5 баллов и меньше – оценка «2». | Критерии для оценочного листа: -организационный момент (готов – 1 балл, не готов – 0 баллов); -устная работа (по 1 баллу за правильный ответ); -открытие нового знания (за каждый устный правильный ответ на вопросы учителя – плюс 1 балл); -формулирование нового знания (понял тему – 1 балл, не понял – 0 баллов); -первичное применение нового правила (самостоятельно, без доски решал все примеры - 4 балла, минус 1 балл за каждый списанный с доски пример); -самостоятельная работа (максимум 4 балла). | Личностные (личностная саморефлексия) |
| Домашнее задание 1–2 минуты | —Откройте дневники, запишем домашнее задание: выполнить № 425, № 426 и выучить правила на страницах 118-119. —Это было домашнее задание для всех, а теперь творческое задание на дом по желанию: составить свои пять примеров на сложение и вычитание обыкновенных дробей с одинаковыми знаменателями, решить их и красиво оформить на формате А4. У нас получится сборник примеров, например, для устной работы. | —Записывают домашнее задание в дневники. | В правом углу доски учитель записывает:
Д/З: № 425, № 426 и правила. + Творческое задание по желанию. | Личностные (важность познания нового) |

















