МОУ средняя общеобразовательная школа №2
Комбинированный урок
«Построение графика функции у =а (х-х0)2 + у0 с помощью сдвига графика функции у = ах2 ».
Алгебра 8 класс.
Урок подготовила и провела
учитель математики
Кочеткова Татьяна Васильевна.
Урок 3: «Функция у= а(х-х0)2+у0»
Слайд 2
Цель нашего урока – научиться строить графики квадратичной функции, представленной в виде у=а(х-х0)2+у0 сдвигом графика функции у=ах2
Слайд 3
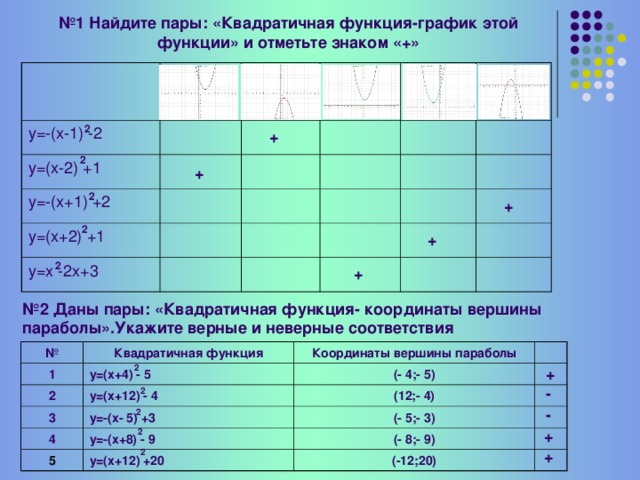
Актуализация: Вспомним, как можно найти координаты вершины параболы, заданной формулой.
1) у=-2(х-7)2+3 (7;3)
2) у=3(х-8)2 (8;0)
3) у=-(х+2)2-6 (-2;-6)
4) у= 4х2 -1 (0;1)
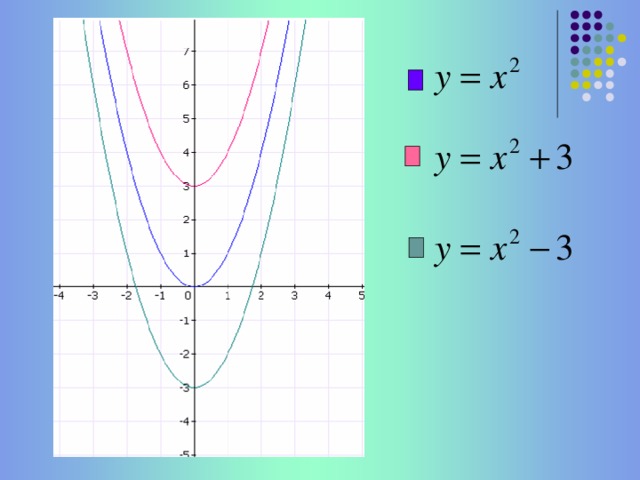
(слайд 4) Найдите соответствие между графиком и формулой
У=х2 – синий у= х2+3 – красный у= х2-3 – зеленый (Зеленый и красный графики можно получить сдвигом. Вопрос сдвигом какого графика , куда и на сколько ?)
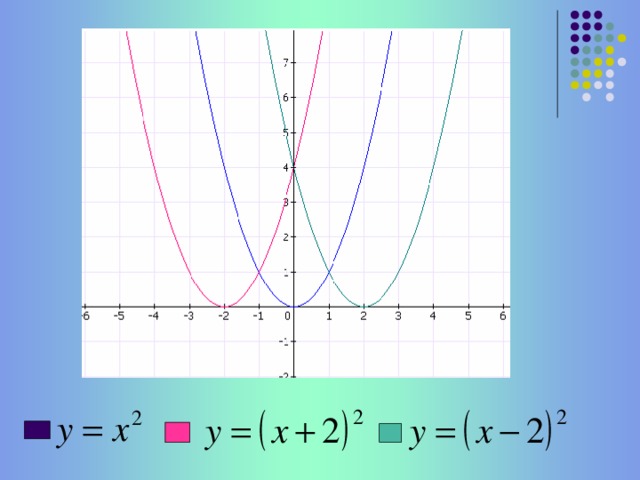
(слайд 5) Установите соответствие между графиком и формулой.
у=х2 –синий у=(х+2)2 –красный у=(х-2)2 –зеленый (Сдвигом какого графика , куда и на сколько могут быть получены зеленый и красный графики)
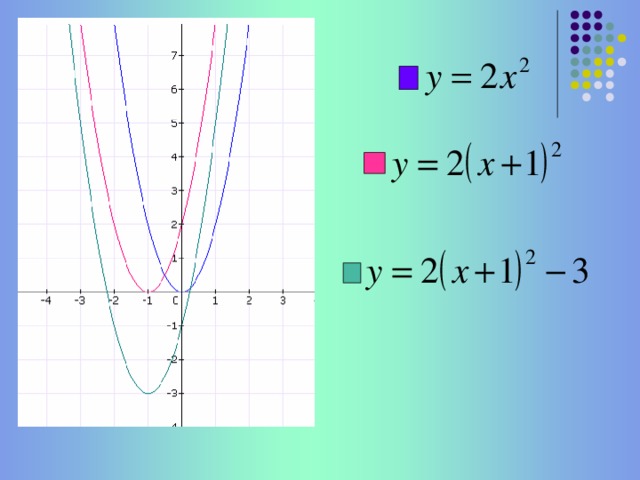
(слайд 6) Установите соответствие между графиком и формулой
У=2х2 –синий у= 2(х+1)2 –красный у=2(х+1)2 – 3 –зеленый
(Влияет ли старший коэффициент на нахождение координат вершины параболы)
(Слайд 7-8) Мотивация и применение умений нахождения вершины параболы к построению графиков.
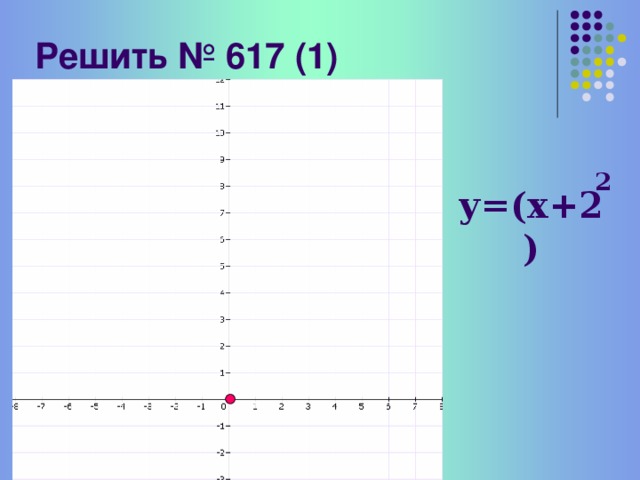
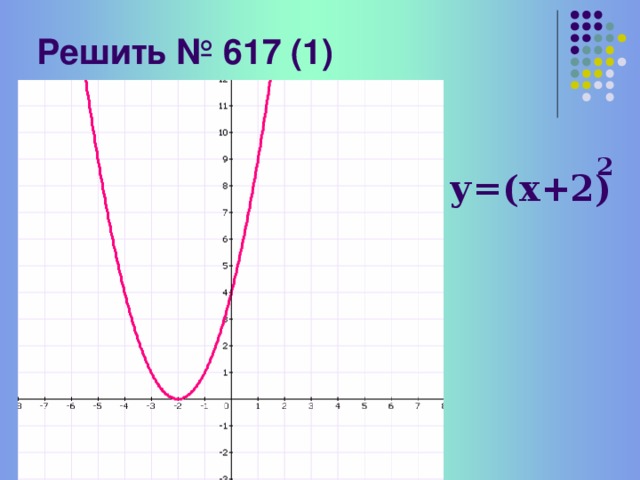
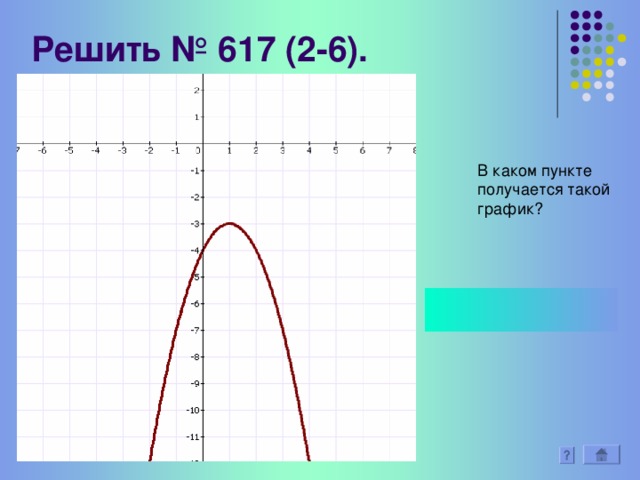
Переходим к письменной работе №617(1)- разбираем совместно построение графика функции у= (х+2)2 .Сдвигом какого графика, куда и насколько может быть получен график функции?
(1-записываем уравнение параболы, 2-двигаем вершину, 3-по шаблону строим график функции у=х2)
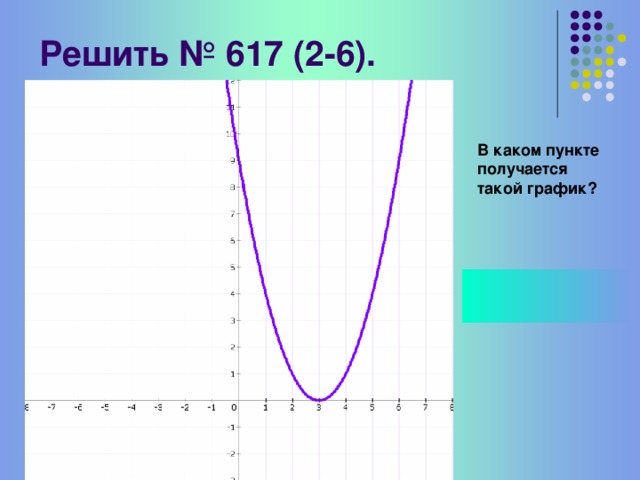
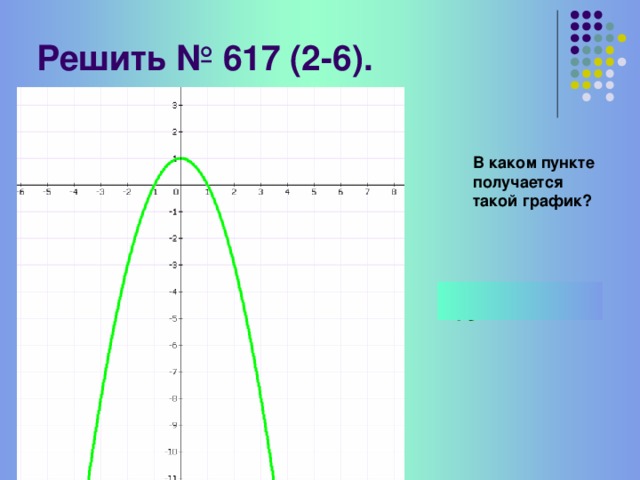
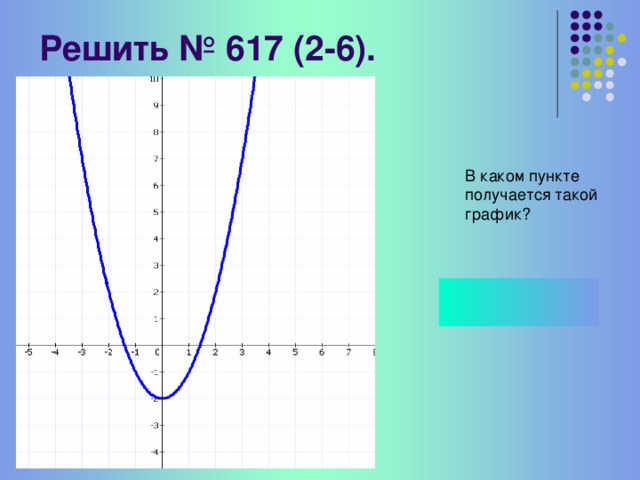
(Слайд 9-13) Закрепление с последующей проверкой
Самостоятельно постройте графики оставшихся функций, после чего выполним совместную проверку. При построении не забудьте про направление ветвей параболы.
Мотивация – проблемная ситуация
Построить график функции у=?х2-2?, содержащей модуль
Для этого вспомним определение модуля ?а?= а, а ≥ 0
-а, а < 0
Таким образом, ребята делают вывод, если по модулю берется целая функция, то все значения функции д.б. не отрицательны.
(Слайд 14) открытие новых знаний
Алгоритм построения:
1)График функции, стоящей под знаком модуля у=х2 -2
2)Зеркально (симметрично) отображаем относительно оси Ох ту часть графика, которая лежит ниже оси наверх
Зеленый график и будет графиком исходной функции
(Слайд 15) Осознание
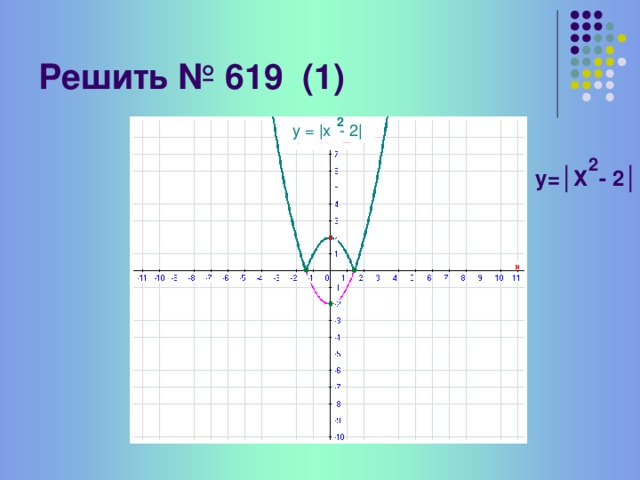
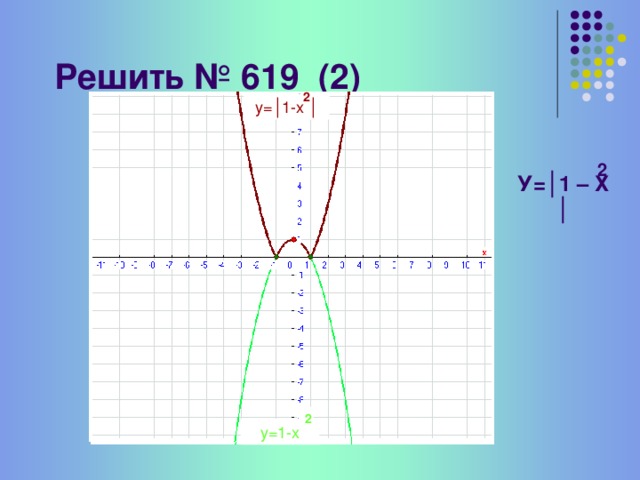
№619(2)
У=?1-х2?
- у=1- х2 –парабола, ветви, которой направлены вниз, полученная сдвигом параболы у=-х2 вверх на 1
2)У=?1-х2?-зеркальное отображение относительно Ох
(Слайд 16) Закрепление
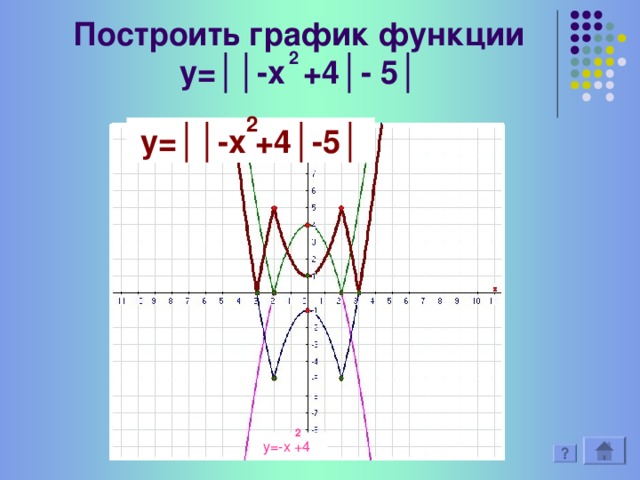
Встречаются более сложные формулы ,задающие квадратичные функции, тогда и графики получаются более интересные и красивые (пример с двойным модулем у=??-х2+4?-5?)
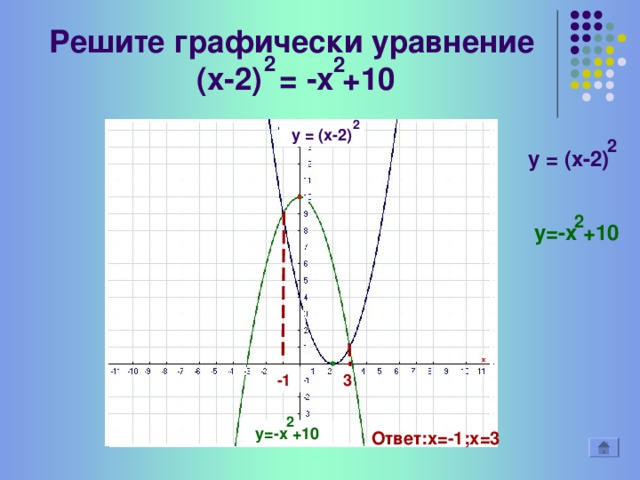
(Слайд 17) Решение квадратного уравнения графически (х-2)2=-х2+10
(Слайд 18) Подведение итогов: Преобразование графика функции у =f(x) в общем виде
(Слайд 19)Проверочная работа
(Слайд 20)Домашнее задание: №608(1,2)-построить графики, №618,№619(3),решить графически уравнения х2+2=-(х+2)2, х2+2= 5(х-3)2
(Слайд 21, 22) Упражнения на быстроту мышления
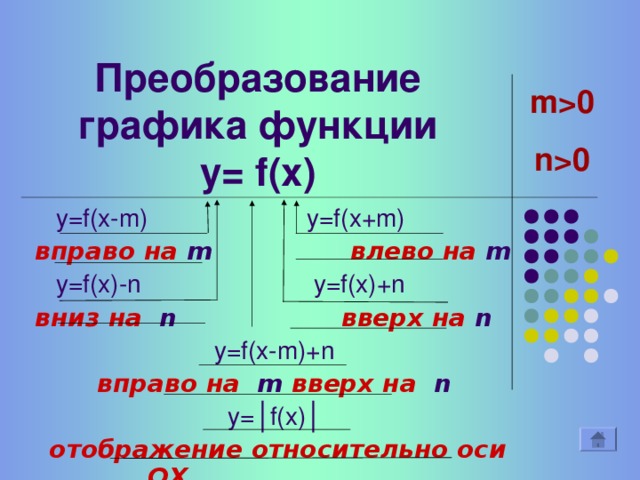
0 n0 Преобразование графика функции y= f(x) y=f(x-m) y=f(x+m) вправо на m влево на m y=f(x)-n y=f(x)+n вниз на n вверх на n y=f(x-m)+n вправо на m вверх на n у = │ f(x) │ отображение относительно оси ОХ" width="640"
