| I. ОРГАНИЗАЦИОННЫЙ МОМЕНТ Задача: Организовать учащихся на урок
Здравствуйте, ребята! Садитесь все на свои места.
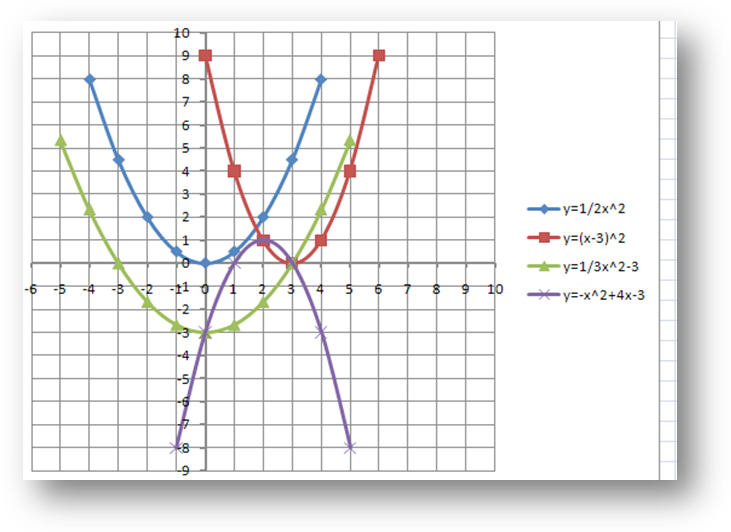
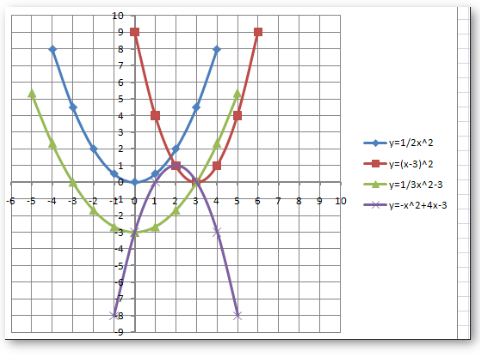
II. ОЗНАКОМЛЕНИЕ УЧАЩИХСЯ С НОВЫМ МАТЕРИАЛОМ Задача: Познакомить учащихся с алгоритмом построения графика параболы при помощи графических средств табличного процессора Подготовительная работа к изучению нового материала Работаем устно. Как называется линия, являющаяся графиком функции �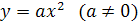 � ? � ? Парабола Посмотрите внимательно на доску. На доске изображены параболы – графики квадратичных функций: 1. у=1/2 x2
2. y=(x-3) 2
3. y=1/3 x2 -3
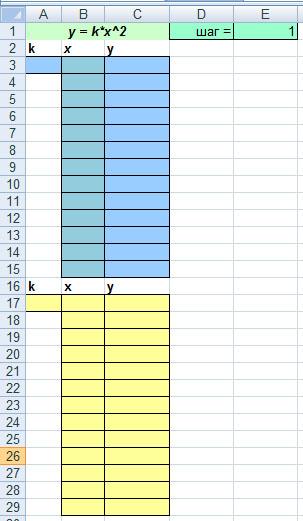
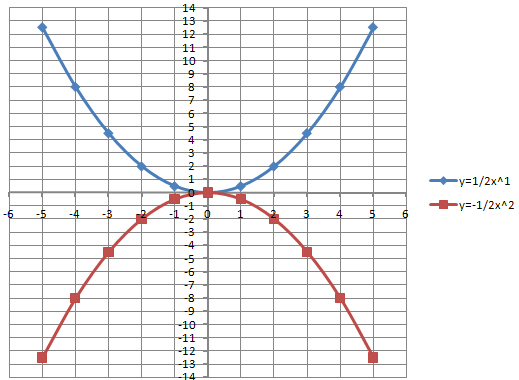
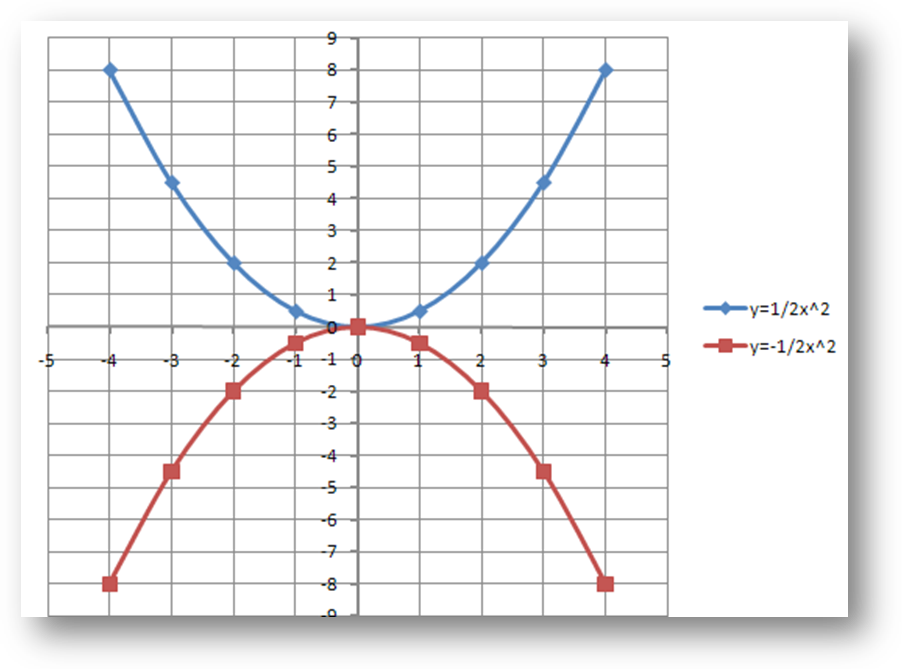
4. y= - x2 +4x-3 Охарактеризуйте каждую из них. 1. у=1/2 x2 Направление ветвей – вверх Уравнение оси симметрии x=0 Координаты вершины (0,0) Область определения (-∞;+∞) 2. y=(x-3) 2 Направление ветвей – вверх Уравнение оси симметрии x=3 Координаты вершины (3,0) Область определения (-∞;+∞) 3. y=1/3x2 -3 Направление ветвей – вверх Уравнение оси симметрии x=0 Координаты вершины (0,-3) Область определения (-∞;+∞) 4. y= - x2 +4x-3 Направление ветвей – вниз Уравнение оси симметрии x=2 Координаты вершины (2,1) Область определения (-∞;+∞) Молодцы! Сообщение темы и цели урока Сегодня на уроке мы научимся получать графики параболы с помощью табличного процессора MS Excel 2007. 3. Формирование знания построения графиков в табличном процессоре Мы знаем, что компьютер – инструмент, который работает с конкретными математическими моделями. Рассмотрим математические модели квадратичной функции. Открываем электронную таблицу Параболы, лист1. Первая математическая модель парабола вида: y=kx2 Задание: Построить графики функции у=1/2 x2 и у = -1/2 x2 в одной системе координат. Для этого сначала укажем коэффициент k для первой и второй функции. Чему равен коэффициент k для функции у=1/2 x2 ? 1/2 Чему равен k для функции у= -1/2 x2 ? -1/2
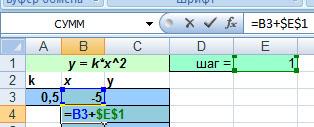
Теперь нужно указать диапазон значений для x. Для этого введем в ячейку для Х любое начальное значение диапазона. Пусть начальным значением будет, например, число -5. Как задать диапазон ячеек изменяющих значение с шагом 1? Задать формулу заморозив значение шага, используя абсолютную адресацию.
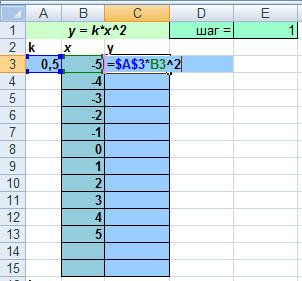
А теперь дублируем формулу с помощью черного крестика в нижнем правом углу. Так как парабола симметрична относительно оси ОY, то дублируем до тех пор пока конечное значение функции не станет = начальному значению функции. Это нужно для того, чтобы точки были симметричны относительно оси ОY. Затем нужно ввести формулу в ячейку для Y. Как записать математическую модель параболы y=kx2 в виде формулы в Excel ? =$A$3*B3^2
Какие значения остаются неизменными? k Что тогда нужно сделать с этой ячейкой? Заморозить. Теперь дублируем эту формулу. Аналогично выполняем для функции у = -1/2 x2
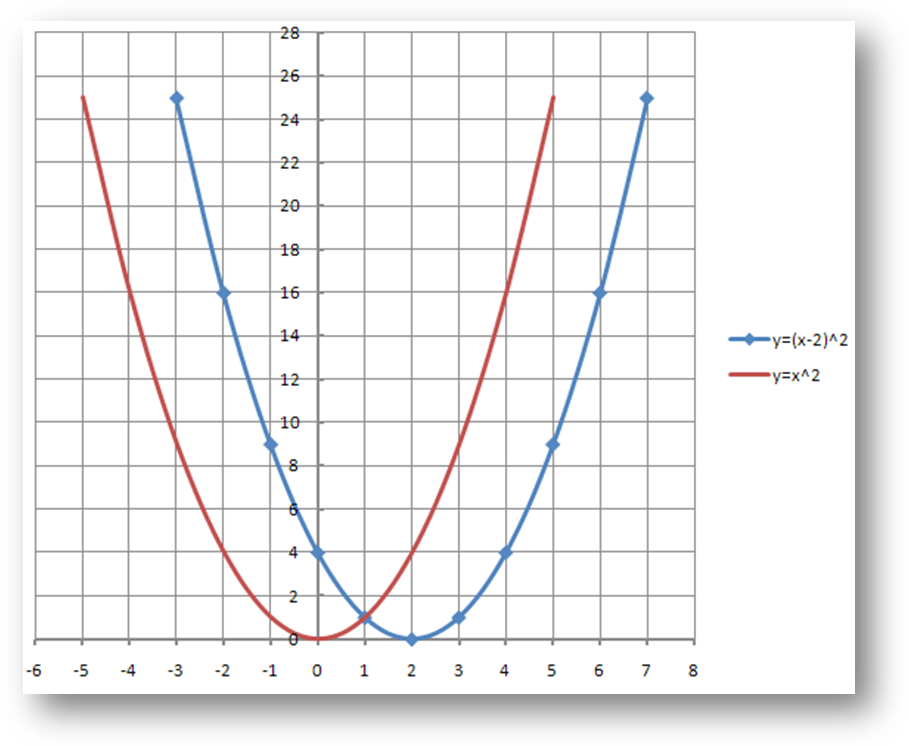
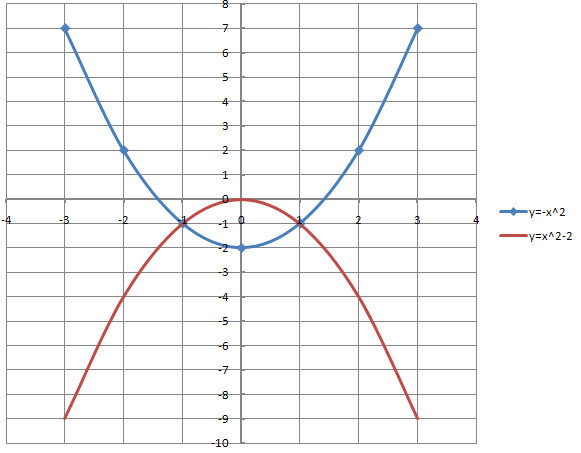
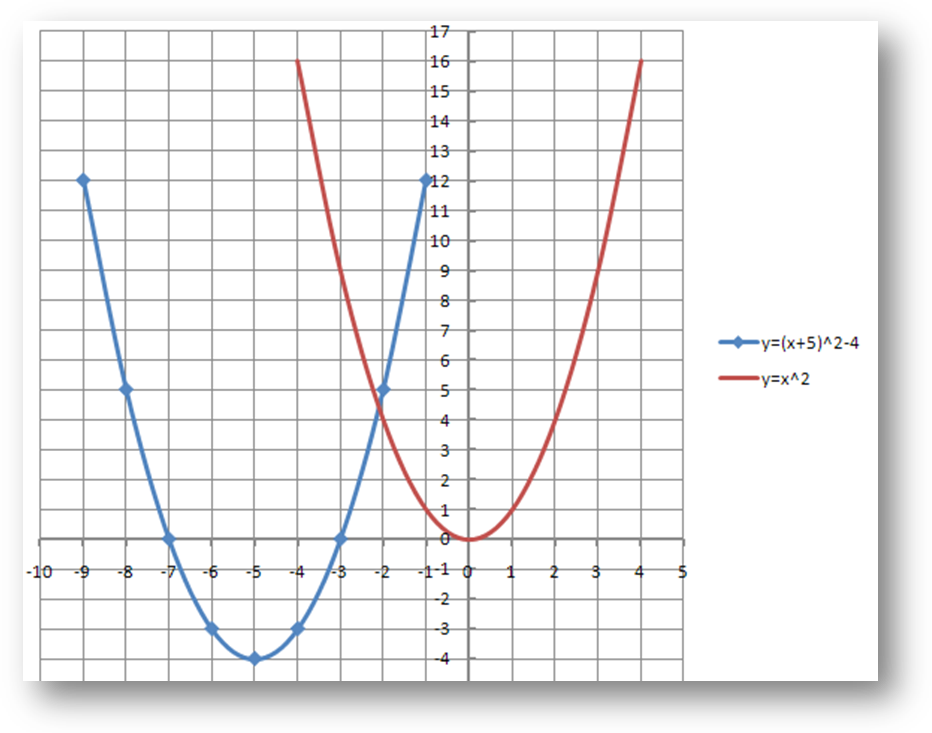
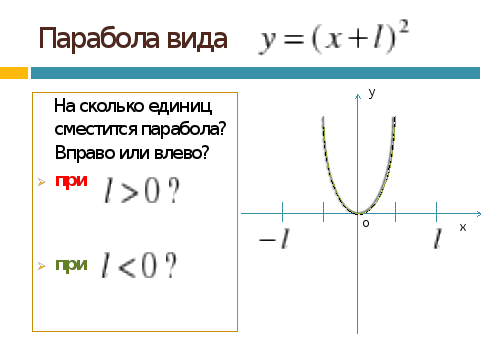
Для построения графика данных функций выбираем ВСТАВКА – ГРАФИК ТОЧЕЧНЫЙ–С ГЛАДКИМИ КРИВЫМИ и МАРКЕРАМИ. Затем ВЫБРАТЬ ДАННЫЕ – ДОБАВИТЬ – указать название ряда, диапазон значений для Х и диапазон значений для Y - ОК. Затем снова добавить и применить уже к значениям второй функции. Теперь рассмотрим вторую математическую модель: y=f(x+l) на примере квадратичной функции.
Итак, мы с вами рассмотрели построение графиков двух математических моделей параболы, а сейчас закрепим полученные знания. III. ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО НА УРОКЕ МАТЕРИАЛА Задача: формировать у учащихся умение получать графики парабол с помощью графических средств табличного процессора. Выполнить практическую работу. Сейчас Вы садитесь за компьютеры по два человека и выполняете данную практическую работу. Всего 5 математических моделей параболы. На отметку «5» необходимо выполнить 5 заданий. На отметку «4» - 3-4 задания. На отметку «3» - 1-2 задания IV. ПОСТАНОВКА ДОМАШНЕГО ЗАДАНИЯ Задача: сообщить учащимся домашнее задание Откройте дневники и запишите домашнее задание: построить графики функций: y=2x2+4; y=2(x+3)2-5; y=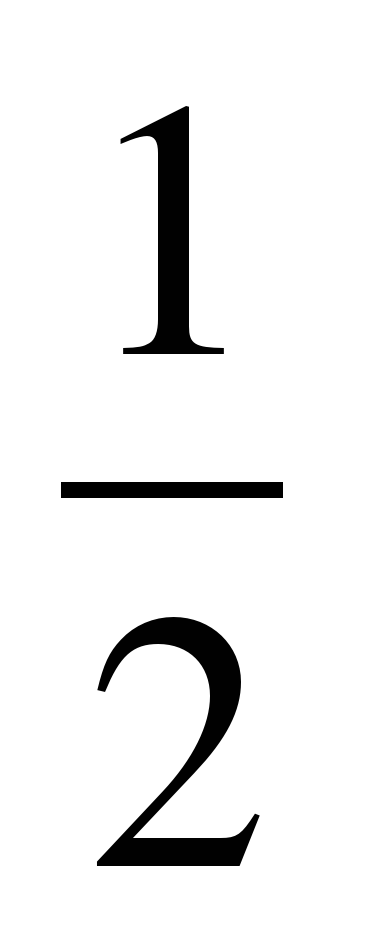 (x-6)2; y= – (x-6)2; y= –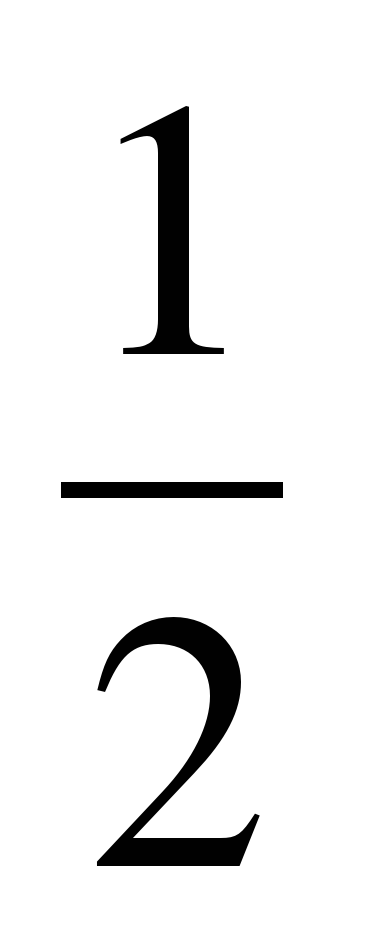 (x-3)2+4 (x-3)2+4 V. ПОДВЕДЕНИЕ ИТОГОВ УРОКА |