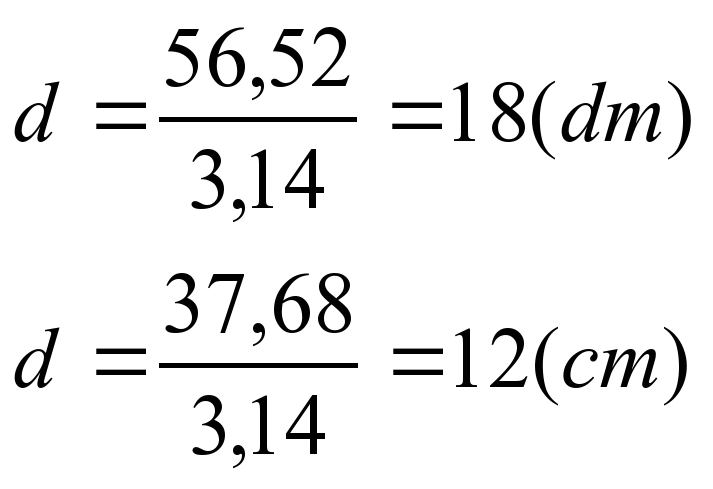| 1.
2.
3.
4.
5.
6.
| Орг. момент - Здравствуйте, садитесь. Мы сегодня на уроке познакомимся с новой темой. Актуализация прежних знаний Округлите число до единиц, десятых долей, сотых долей 32,829 Найдите среднее арифметическое чисел: 4,8; 6,1; 7,1. Формирование новых знаний Если острие ножки циркуля установить неподвижно в точке О, а другую ножку с грифелем вращать на плоскости листа (или доски), то грифель опишет замкнутую кривую линию, все точки которой будут равноудалены от одной точки О. Эта кривая линия называется окружностью. Точка О – центр окружности. Отрезок, соединяющий любую точку окружности с ее центром, называется радиусом окружности. Обозначим радиус r. Все радиусы окружности равны между собой. Отрезок, проходящий через центр окружности и соединяющий две ее точки, называется диаметром окружности (d). Диаметр вдвое больше радиуса (d=2r). Концы диаметра делят окружность на две равные части. Возьмем круглый стакан, поставим на лист бумаги и обведем его карандашом. На бумаге получится окружность. Если «опоясать» стакан ниткой, а потом распрямить ее, то длина нитки будет приближенно равна длине нарисованной на листке окружности. Длина окружности тем больше, чем больше ее диаметр. Длина окружности прямо пропорциональна длине ее диаметра. Поэтому для всех окружностей отношение длины окружности к длине ее диаметра является одним и тем же числом. Это отношение обозначают греческой буквой π («пи»). Если длину окружности обозначить буквой С, а диаметр – d, то С:d=π или С=πd. Т.к. d=2r, то С=πd=2rπ – формула длины окружности. Подсчеты показали, что с точностью до десятитысячных π ≈ 3,1416. Если значение округлить до сотых, то получим значение π=3,14 (π ≈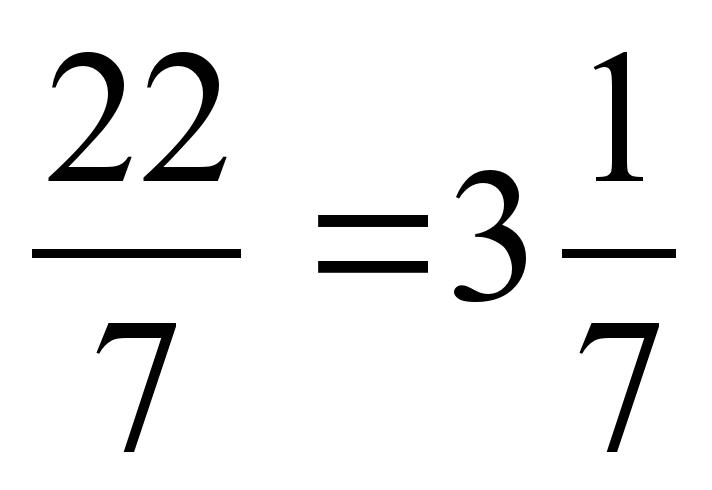 ). ). Закрепление изученного материала № 833 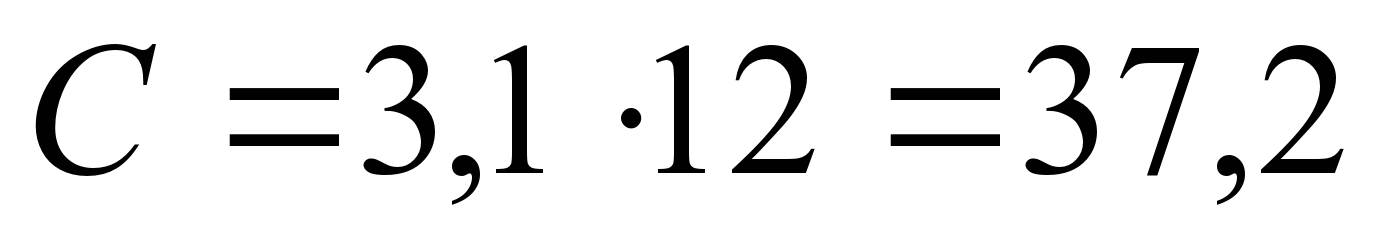 (см) (см)
№ 831 
№ 832 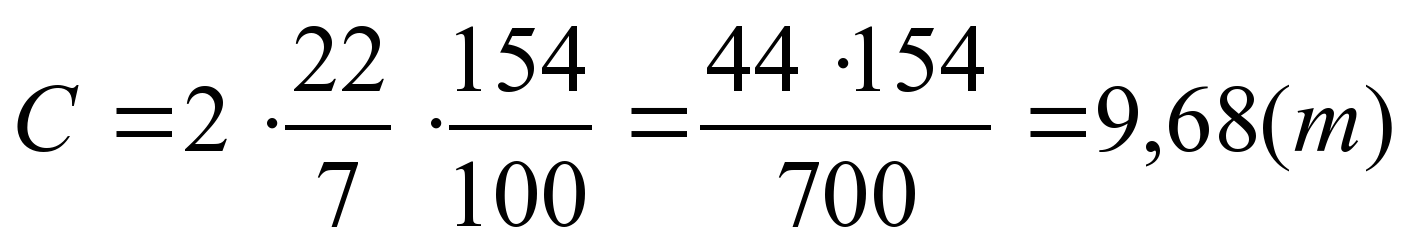
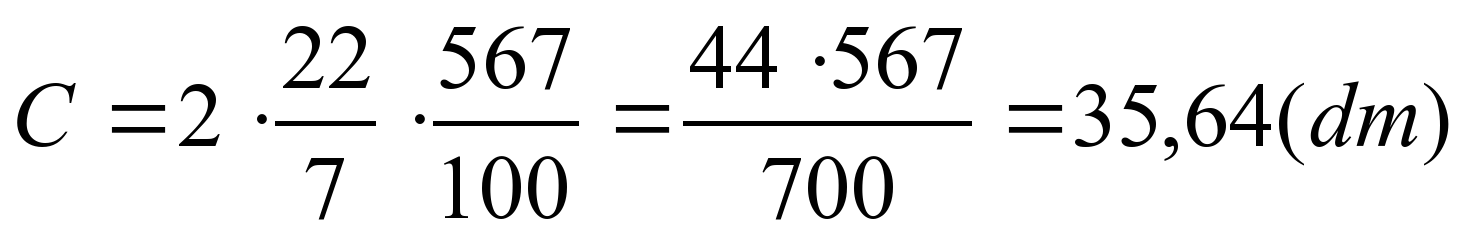
№ 842 (а, б)
№ 834 
№ 835 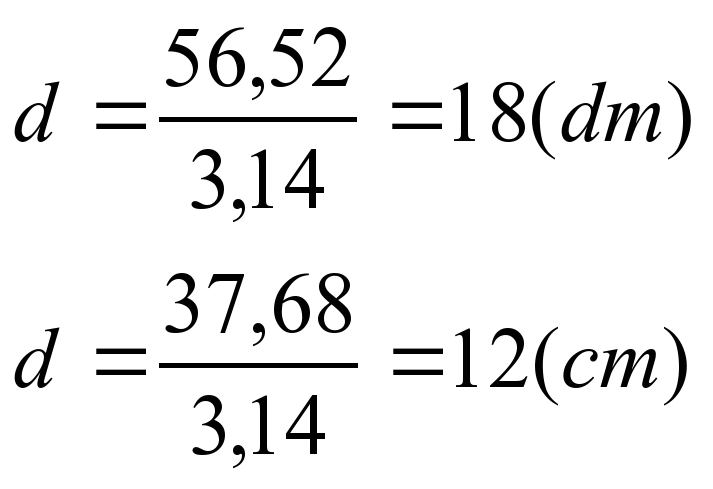
Домашнее задание п.24 № 851 № 852 № 853 № 854
Итог урока
|
Устно.
Учитель объясняет.
Формулы на доске.
На доске.
3 уч-ся на доске.
2 уч-ся на доске.
Устно.
На доске.
На доске, самостоятельно.
Д/з на доске. |