Конспект урока математики
по теме «Координатная плоскость», 6 класс.
Цели урока:
Обобщение и закрепление понятий координатная плоскость; координаты точки.
Обобщение и закрепление построений точки по её координатам и нахождение координат точки.
Развитие интереса учащихся к предмету.
Развитие внимательности, точности, сообразительности.
Расширение кругозора учащихся.
Оборудование: портреты ученых-математиков, учебник, карточки-задания,
карточки-координатная плоскость, тест.
План урока:
Организационный момент.
Проверка домашнего задания:
Устный опрос:
Практическая часть:
Рене Декарт.
Карл Гаусс.
Пифагор.
Самостоятельная работа:
Задание на дом.
Итоги урока.
Ход урока:
Организационный момент.
На прошлых уроках мы с вами побывали в зоопарке, рисовали фигурки различных животных; рассматривали картины в картинной галерее, некоторые из работ учащихся представлены в классе и сейчас; также побывали в мире созвездий, а дома вы продолжили знакомство с созвездиями.
Истории созвездий очень интересны. Давным-давно наблюдатели неба объединили наиболее заметные группы звезд в созвездия и дали им различные наименования. Это были имена мифических героев или животных, персонажей легенд и сказаний.
На первый взгляд, названия созвездий кажутся странными, ведь в расположении звезд трудно или даже невозможно рассмотреть то, о чем говорит название созвездия. Ведь, например, большая медведица напоминает…(ковш).
Проверка домашнего задания:
№ 1*. Постройте на одной координатной плоскости точки, последовательно соединив их отрезками:
(6; 6) , (3; 7) , (0; 7,5) , (-3; 5,5) , (-5; 7) , (-8; 5) , (-6; 3) , (-3; 5,5).
( -15; -7) , (-10; -5) , (-6; -5,5) , (-3; -6) , (-1; -10) , (5; -10) , (6; -6) , (-3; -6).
Газета «Математика» № 5- 2008-6.
Устный опрос:
Вопросы.
Вспомните, что представляет собой прямоугольная система координат?
(Прямоугольная система координат – это две взаимно перпендикулярные прямые с выбранными направлениями и единицей длины.)
Дайте определение координатной плоскости.
(Плоскость, на которой выбрана система координат, называют координатной плоскостью. Пример: лист тетради, на котором нарисована система координат.)
Что мы называем координатами точки?
(Абсциссу х и ординату у заданной точки)
Как называют координатную прямую х, ось Ох?
(Ось абсцисс)
Как называют координатную прямую у, ось Оу?
(Ось ординат)
Практическая часть:
Рене Декарт.
Кто из вас, ребята, знает, с именем какого выдающегося математика связано понятие прямоугольная система координат? (Рене Декарт)
Введенные на плоскости координаты х и у называют декартовыми по имени французского математика Рене Декарта.
Вы видите портрет Рене Декарта, французского философа, математика, физика и физиолога.
№ 1. Заполните таблицу координатами точек, используя данный чертеж.
(ПРИЛОЖЕНИЕ 1)
РЕНЕ ДЕКАРТ – французский философ, математик, физик.
| Д | Е | К | А | Р | Т |
| ( ; ) | ( ; ) | ( ; ) | ( ; ) | ( ; ) | ( ; ) |
Ученик 6 класса ______________________________________
№ 2. Расшифруйте высказывание немецкого математика Карла Гаусса. Запишите название точки, по известным координатам, используя рисунок.
(ПРИЛОЖЕНИЕ 2)
| ( 11; 4)
| ( 6; 1)
| ( 1; 4) | ( 15; 5) | ( 11; 4) | ( 6; 1) | ( 1; 4) | ( 9; 6) | ( 2; 7) | ( 6; 1) |
|
|
|
|
|
|
|
|
|
|
|
| ( 4; 5)
| ( 6; 1) | ( 12; 2) | ( 9; 6) | ( 4; 5) | ( 6; 1) |
|
|
|
|
|
|
|
| ( 7; 4) | ( 6; 1) | ( 14; 1) | ( 2; 7)
|
|
|
|
|
|
Высказывание немецкого математика Карла Гаусса. Ученик 6 кл ____________________
(«Математика – царица наук»)
Вспомним, ребята, слова известного физика Эдисона «Гений состоит из 1 % вдохновения и 99 % потения», т.е. только благодаря великому труду и старанию можно достичь успехов.
«Все есть число», «числа правят миром» - искренне верил Пифагор. Учение о числах было одной из составных частей его религии. Он считал, что можно выразить все закономерности в мире через числа. Пифагорейцы обожествляли числа и геометрические фигуры, а их богатая фантазия наделяла их невероятными свойствами.
Число 1 означало огонь, 2 – землю, 3 – воду, 4 – воздух.
№ 3. Постройте на координатной плоскости символы любви и разума.
Работа по вариантам.
1 вариант: (2;2), (0;2), (-1;1), (1;1), (0;-1), (-2;-1).
2 вариант: (4;1), (6;1), (4;-2) и (4;-1), (5;-1).
Самостоятельная работа:
Каждая точка с целочисленными координатами обозначена буквой. Например, точка с координатами (0;0) есть точка А; (2;1) – точка Ж, точка Ч (-1;2) и т.д. Такую сетку можно использовать в качестве шифра.
Расшифруйте запись: (-1;-2), (2;-3), (-2;-3), (1; -1), (0;1), (1;-1), (-1;0), (-2;0), (0;-2).
(Ты молодец)
Итоги урока.
Задание на дом:
№ 4. Постройте рисунок на координатной плоскости.
А ( 0 ; 3) , В ( -0,8 ; 1) , С ( -3 ; 1) , D ( -1,2 ; 0) , Е ( -2 ; -2) , F ( 0 ; -1) , G ( 2 ; -2) , К (1,2 ; 0) , L ( 3 ; 1) , М ( 0,8 ; 1) , А ( 0 ; 3) .
Этот знак в школе Пифагора, считался символом дружбы, он был чем-то вроде талисмана, которым одаривали друзей, тайным знаком, по которому пифагорейцы узнавали друг друга. В средние века он предохранял от нечистой силы, что, впрочем, не мешало называть его «лапой ведьмы».
5

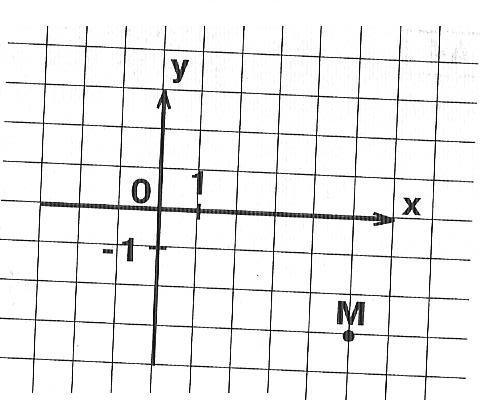 Рис.1
Рис.1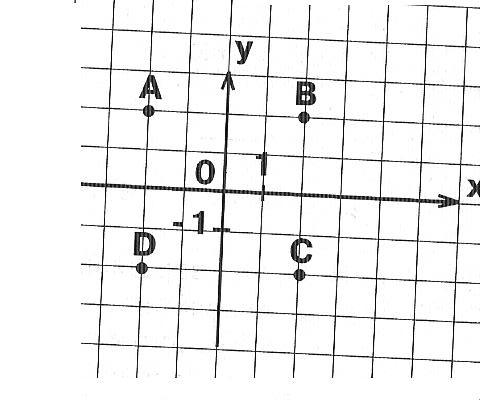 Рис.2
Рис.2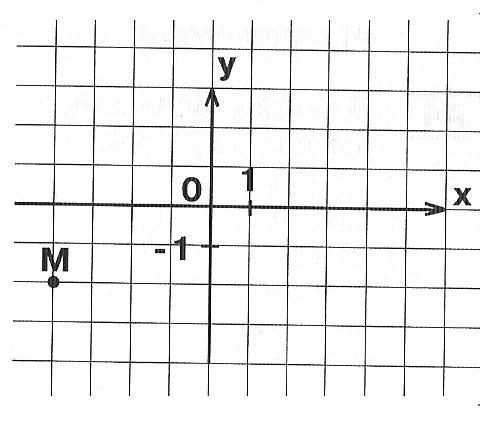 Рис.1
Рис.1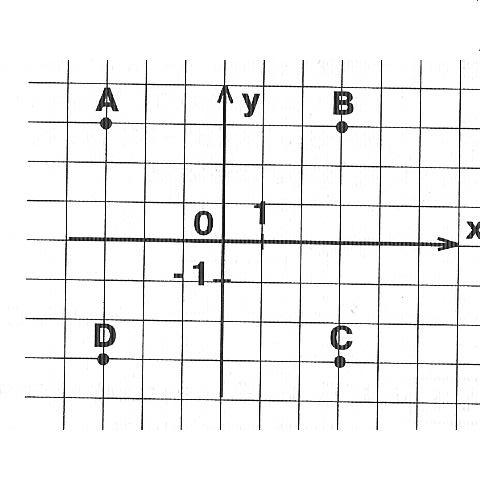 Рис.2
Рис.2
















