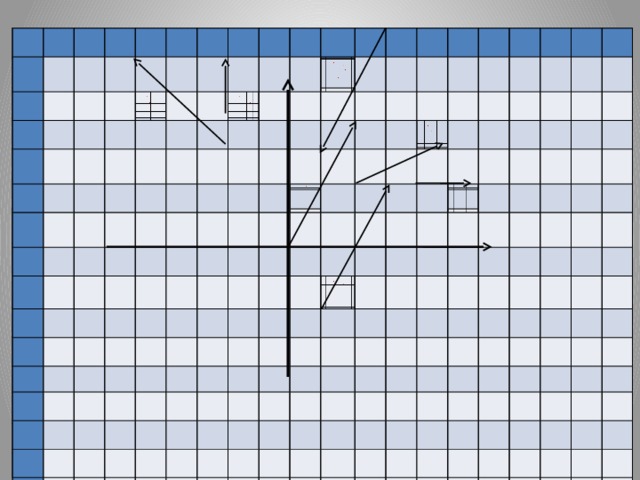
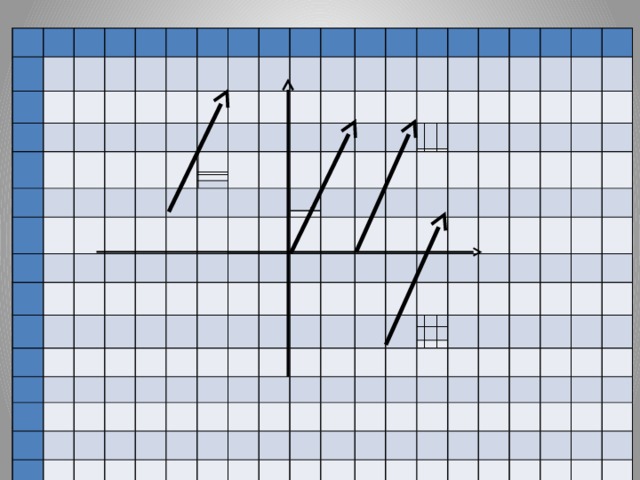
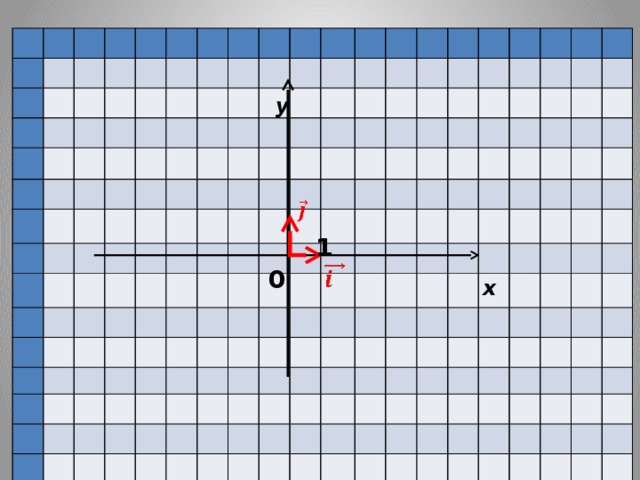
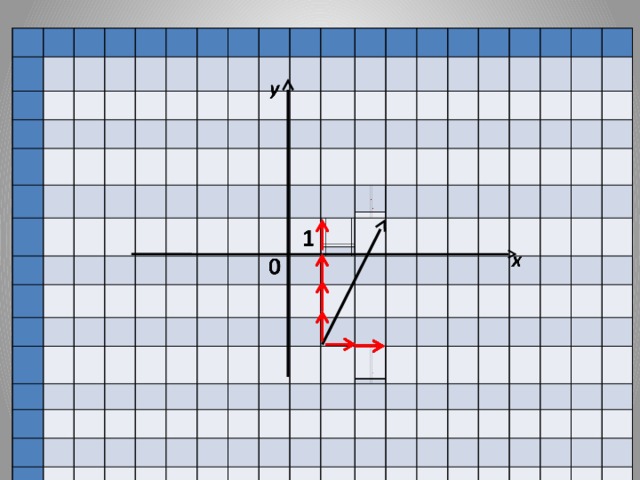
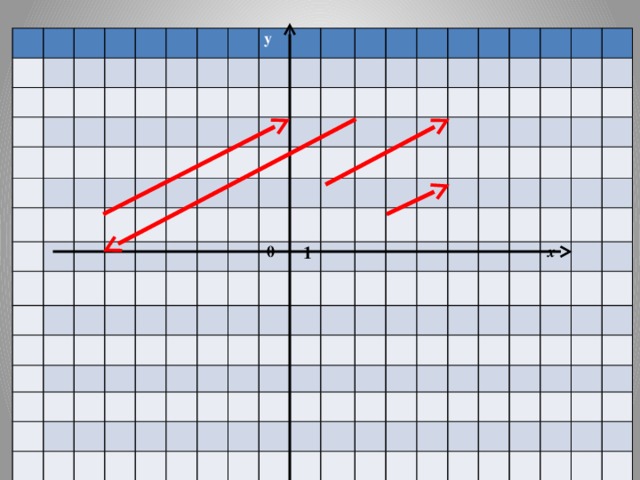
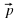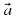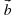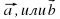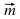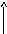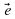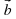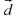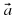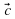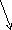| Работать будем с кластерами, которые пока не заполнены.(Приложение№2) Запишите тему: Координаты вектора Понятие координат вектора кардинально отличается от понятия координат точки. Координаты точки- однозначно определяют её место, а вот координаты вектора нет. Посмотрите на слайд (№): все эти векторы имеют одинаковые координаты. Координаты вектора записывают иначе, чем координаты точки. Обозначение 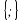 Введём понятие единичных векторов, которые отложим от начала координат. Предположите, что это за векторы. Обозначаются 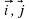 . . Их взаимное расположение? Аналогичное понятие перпендикулярности – ортогональные векторы. Также эти векторы называют базис. - Любой ли вектор 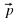 можно разложить по векторам можно разложить по векторам 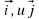 ? ? -Обоснуйте ваше мнение
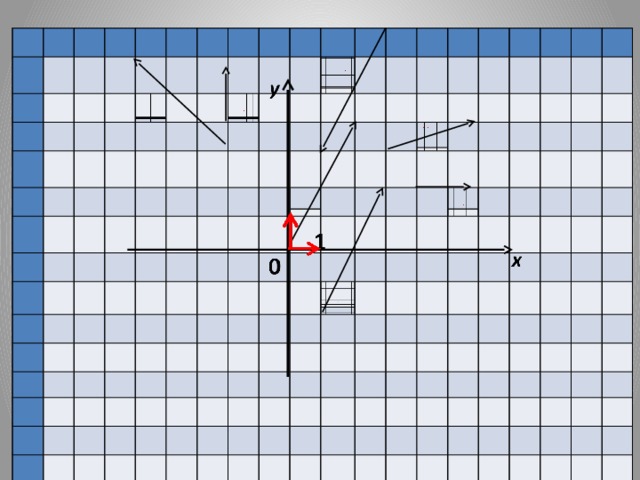
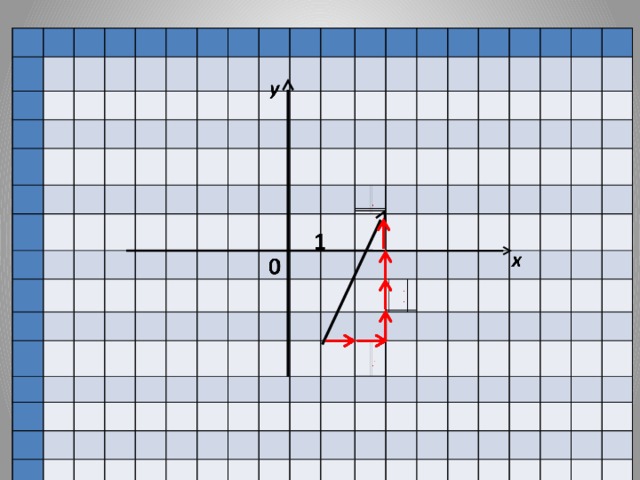
Запишем: 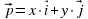 Коэффициенты разложения вектора по координатным векторам и есть координаты вектора. Сколько возможностей разложить вектор по координатным векторам? Определим координаты векторов приведенных в кластере. (Аналогичный рисунок на слайде № 7). Определять координаты можно двумя способами: по правилу треугольника, по правилу параллелограмма. (слайд № 8,9) Запишем в рабочих тетрадях разложение данных векторов по координатным векторам. -Сравните векторы и их координаты: 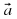 и и 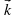 , , 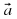 и и 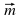
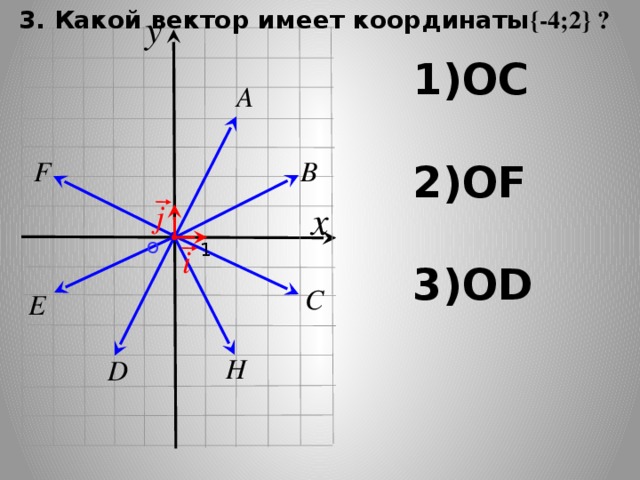
- Сформулируйте выводы о координатах равных векторов и координатах противоположных векторов. - Рассмотрим обратную задачу: по координатам векторов- разложить их по координатным векторам. №920 (а,в,д) -Как разложить нулевой вектор по координатным? -Чему равны координаты нулевого вектора? -Посмотрите на слайд и предположите, как связаны координаты коллинеарных векторов. - Поиграем в игру: Если я правильно назвала пару коллинеарных векторов, вы встаёте и хлопаете на головой, если нет- встаете и поворачиваете туловищем влево-вправо. -В нашем кластере осталось незаполненное поле ПРАВИЛА. -Предлагаю открыть учебник на стр 230-231 и поработать в группах (3 гр). Каждая группа работает над одним правилом, кратко записывать его в кластер и через 4-5 минут один из группы объяснит его у доски. Объяснение правил учащимися. Учитель направляет - Предлагаю применить правила в конкретной задаче. № 926 (б,г). (Учитель показывает на одном примере оформление, учащиеся продолжают остальные задания выполнять с места с комментарием) -Рассмотрим задания составлены по типу заданий из ОГЭ. Задания на слайде № 1 |
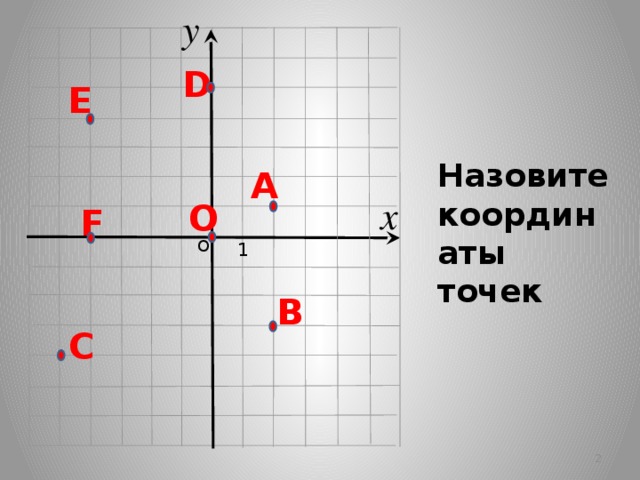
Отмечают в кластере сходства и различие координат вектора и координат точки.
Высказывают предположения, отмечают в системе координат, записывают определение в кластер
Да По теореме о разложении векторов по двум неколлинеарным векторам
Единственным образом.
Комментируют, записывают
Рассуждают. Делают вывод .
Формулируют, записывают в кластер.
Решают у доски.
Рассуждают. 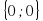
Выявляют закономерность.
Ребята смотрят на слайд и выполняют движения.
Объединяются в группы (учитель заранее обговаривает с ребятами состав групп), работают.
Защищают своё правило. Остальные кратко фиксируют его в кластер
Работают в тетрадях
Выполняют задания | 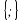
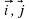 .
.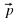 можно разложить по векторам
можно разложить по векторам 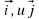 ?
?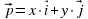
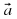 и
и 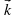 ,
, 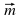
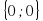
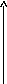



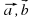 - неколлинеарные векторы
- неколлинеарные векторы