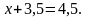| Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу) | 6.2.2.2 знать определение линейного уравнения с одной переменной, равносильных уравнений; |
| Цели урока | Учащиеся будут: знать: определение равносильных уравнений, свойства равносильных уравнений какие преобразования приводят к равносильным уравнениям и способы их применения к решению простейших уравнений с одной переменной; уметь:
|
| Критерии оценивания | Учащийся: знает: свойства равносильных уравнений и способы их применения к решению простейших уравнений с одной переменной; умеет:
|
| Языковые цели | Учащиеся будут:
Предметная лексика и терминология:
Серия полезных фраз для диалога/ письма: Если к обеим частям уравнения прибавить одно и то же число, то. Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то. Если в уравнении какое-нибудь слагаемое перенести из одной части в другую, изменив его знак, то. |
| Привитие ценностей | Умение учиться, добывать самостоятельно информацию, анализировать ситуацию, адаптироваться к новым ситуациям, ставить проблемы и принимать решения, работать в команде, отвечать за качество своей работы, умение организовывать свое время. Привитие ценностей осуществляется посредством работ, запланированных на данном уроке. |
| Межпредметные связи | Взаимосвязь с жизнью, через решение практических задач. |
| Предварительные знания | Знание нахождение неизвестных компонентов действий Умение решать элементарные уравнения. |
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Равносильные уравнения. Линейное уравнение с одной переменной.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Равносильные уравнения. Линейное уравнение с одной переменной.»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1630 руб.
2710 руб.
1800 руб.
3000 руб.
1690 руб.
2820 руб.
1540 руб.
2560 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
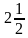 ; с) –4, получим уравнения:
; с) –4, получим уравнения: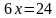 ;
;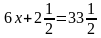 ;
;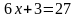 .
.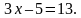
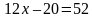 .
.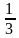 , получим уравнения:
, получим уравнения: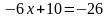 ; б)
; б) 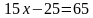 ; в)
; в) 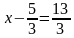 .
.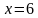 . Значит, все они равносильны данному уравнению.
. Значит, все они равносильны данному уравнению.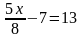 (1)
(1)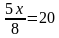
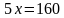 равносильно (2), а следовательно, и данному.
равносильно (2), а следовательно, и данному.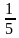 ), получим уравнение x = 32,
), получим уравнение x = 32,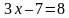 . Доказать, что если прибавить к обеим частям этого уравнения буквенное выражение –2x, то получится равносильное уравнение.
. Доказать, что если прибавить к обеим частям этого уравнения буквенное выражение –2x, то получится равносильное уравнение.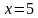 .
.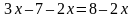 ;
; 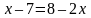 .
.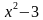 .
.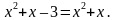
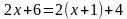 имеющее любое значение неизвестного. Доказать, что умножив обе его части на 3; –2; 0,5, получим равносильные уравнения.
имеющее любое значение неизвестного. Доказать, что умножив обе его части на 3; –2; 0,5, получим равносильные уравнения.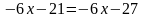 ;
;