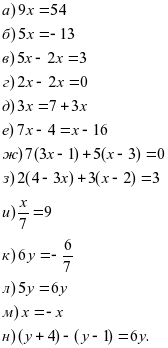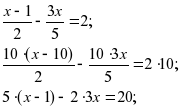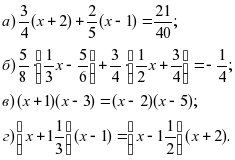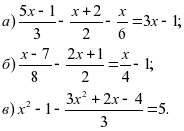Дифференцированные вопросы и задания по теме «Линейные уравнения с одной переменной»
Понятие уравнения с одной переменной. Равносильные уравнения. Решение линейных уравнений
Требования к уровню подготовки учащихся
Уровень обязательной подготовки
знать определение уравнения, корня уравнения, определение уравнения с одной переменной; знать, что означает решить уравнение;
иметь представление о равносильных уравнениях;
знать свойства уравнений;
уметь проверять, является ли данное число корнем уравнения;
уметь решать несложные уравнения с одной переменной;
уметь использовать условие равности произведения нулю во время решения уравнений.
Высокий уровень
знать строгое определение уравнения с одной переменной;
знать определение уравнения первой степени с одной переменной;
решать линейные уравнения с дробными коэффициентами;
уметь доказывать равносильность уравнений;
уметь решать уравнения с модулем;
уметь решать уравнения с параметром;
уметь определять и доказывать количество корней линейного уравнения с одной переменной.
1. Актуализация знаний
1. Решите уравнения:
А. 3,7 + х = 4; Б. 8х = - 16; В. х - 1 = 2 ; Г. х : = 1;
Д. 5 – х = 8,4 Е. 2 : х = 4.
2. Найдите наименьший общий знаменатель дробей
А.
3. Выполните умножение:
2. Объяснение нового материала
1) Определение уравнения
2) Уравнение с одной переменной
3) Что значит решить уравнение?
4) Понятие уравнение первой степени с одной переменной
5) Корень уравнения
6) Равносильные уравнения
7) Свойства уравнений
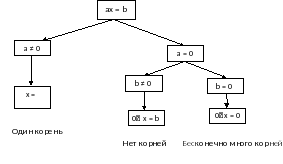
8) Алгоритм решения линейного уравнения с одной переменной:
Выполнить тождественные преобразования в двух частях уравнения, если это необходимо.
Перенести слагаемые, содержащие переменную в одну часть уравнения, а слагаемые без переменной в другую часть, меняя их знаки на противоположные.
В каждой части уравнения привести подобные слагаемые (привести уравнение к виду ах = b .
аx = b
а ≠ 0
а = 0
x =
b ≠ 0
b = 0
0?x = 0
0? x = b
Один корень
Нет корней
Бесконечно много корней
Решите получившееся уравнение по схеме
Пример. Решите уравнение
Вопросы и задания
?. Является ли линейным уравнение
А. = 3 Б. 5х2 = 4,5 В. 5 + х = - 0,1
?. Является ли уравнением первой степени с одной переменной следующие уравнения? Ответ объясните.
А. 3 х2 = 8 Б. = 5 В. 6х = 7х – 1 Г. 7 – х = 6 – х
?. Является ли число 2 корнем уравнения
А. – 5 ? (х – 2) = 0 Б. 3 х2 -2 = 5
¡. Составьте уравнение, корнем которого является число 5
А. Уравнение является линейным
Б. Уравнение не является линейным
?. Решите уравнения:
?. Закончить решение уравнения:
¡. Решите уравнения:
®. Решите уравнения:
Типовые задания для контрольной работы
1?. Определите какое уравнение является уравнением первой степени с одной переменной:
А. 3х + 1 = 20; Б. 0 х = 13; В. 0х = 0
2?. Является ли число 8 корнем уравнения:
А. 2х +3 = 19; Б. 25х – 56 = 10?
3?. Равносильны ли уравнения:
А. 5х = 25 и х – 5 = 0; Б. 0х = 2 и 6х = 0?
4?. Найдите корень уравнения:
А. – 5 х = 25; Б. 9х – 14 = 6х + 7; В. 2х – 4 = - 3(4 – 2х) – 6.
5?. Решите задачу:
Периметр прямоугольника 56 см, его длина на 8 см больше, чем ширина. Найдите стороны прямоугольника.
6¡. Решите уравнения:
А. – (4х + 0,2) = 3(1 – 2х); Б. ; В. |3 – x| = 6;
Г. 4(0,25x – 6) = 8(0,125x +3); Д®. (|x| - 10)(|x| +4) = 0.
7¡. При каком значении переменной т уравнение (т – 3)х = 18:
А. имеет корень, равный 6; Б. не имеет корней.
8¡. Решите задачу
Из двух пристаней, расстояние между которыми 57 км, навстречу друг другу вышли два катера, собственные скорости которых равны. Катер, который идет по течению реки до встречи плыл 1 час, а катер, плывший против течения – 2 часа. Найдите собственную скорость катеров, если скорость течения реки 3 км/ч.
9®. Решите задачу.
Поезд прошел пути со скоростью 60 км/ч, потом задержался на 6 мин. Чтобы прибыть в конечный путь вовремя, остальной участок пути шел со скоростью 75 км/ч. Найдите расстояние, которое прошел поезд.
Просмотр содержимого документа
«Дифференцированные задания "Линейные уравнения с одной переменной" »
Дифференцированные вопросы и задания по теме «Линейные уравнения с одной переменной»
Понятие уравнения с одной переменной. Равносильные уравнения. Решение линейных уравнений
Требования к уровню подготовки учащихся
Уровень обязательной подготовки
знать определение уравнения, корня уравнения, определение уравнения с одной переменной; знать, что означает решить уравнение;
иметь представление о равносильных уравнениях;
знать свойства уравнений;
уметь проверять, является ли данное число корнем уравнения;
уметь решать несложные уравнения с одной переменной;
уметь использовать условие равности произведения нулю во время решения уравнений.
Высокий уровень
знать строгое определение уравнения с одной переменной;
знать определение уравнения первой степени с одной переменной;
решать линейные уравнения с дробными коэффициентами;
уметь доказывать равносильность уравнений;
уметь решать уравнения с модулем;
уметь решать уравнения с параметром;
уметь определять и доказывать количество корней линейного уравнения с одной переменной.
1. Актуализация знаний
1. Решите уравнения:
А. 3,7 + х = 4; Б. 8х = - 16; В. х - 1 = 2; Г. х : = 1;
Д. 5 – х = 8,4 Е. 2 : х = 4.
2. Найдите наименьший общий знаменатель дробей
А.
3. Выполните умножение:
2. Объяснение нового материала
1) Определение уравнения
2) Уравнение с одной переменной
3) Что значит решить уравнение?
4) Понятие уравнение первой степени с одной переменной
5) Корень уравнения
6) Равносильные уравнения
7) Свойства уравнений
8) Алгоритм решения линейного уравнения с одной переменной:
Выполнить тождественные преобразования в двух частях уравнения, если это необходимо.
Перенести слагаемые, содержащие переменную в одну часть уравнения, а слагаемые без переменной в другую часть, меняя их знаки на противоположные.
В каждой части уравнения привести подобные слагаемые (привести уравнение к виду ах = b .
Решите получившееся уравнение по схеме
Пример. Решите уравнение
Вопросы и задания
1. Является ли линейным уравнение
А. = 3 Б. 5х2 = 4,5 В. 5 + х = - 0,1
2. Является ли уравнением первой степени с одной переменной следующие уравнения? Ответ объясните.
А. 3 х2 = 8 Б. = 5 В. 6х = 7х – 1 Г. 7 – х = 6 – х
3. Является ли число 2 корнем уравнения
А. – 5 ∙ (х – 2) = 0 Б. 3 х2 -2 = 5
4. Составьте уравнение , корнем которого является число 5
А. Уравнение является линейным
Б. Уравнение не является линейным
5. Решите уравнения:
6. Закончить решение уравнения:
7. Решите уравнения:
8. Решите уравнения:
Типовые задания для контрольной работы
1. Определите какое уравнение является уравнением первой степени с одной переменной:
А. 3х + 1 = 20; Б. 0 х = 13; В. 0х = 0
2. Является ли число 8 корнем уравнения:
А. 2х +3 = 19; Б. 25х – 56 = 10?
3. Равносильны ли уравнения:
А. 5х = 25 и х – 5 = 0; Б. 0х = 2 и 6х = 0?
4. Найдите корень уравнения:
А. – 5 х = 25; Б. 9х – 14 = 6х + 7; В. 2х – 4 = - 3(4 – 2х) – 6.
5. Решите задачу:
Периметр прямоугольника 56 см, его длина на 8 см больше, чем ширина. Найдите стороны прямоугольника.
6. Решите уравнения:
А. – (4х + 0,2) = 3(1 – 2х); Б. ; В. |3 – x| = 6;
Г. 4(0,25x – 6) = 8(0,125x +3); Д. (|x| - 10)(|x| +4) = 0.
7. При каком значении переменной т уравнение (т – 3)х = 18:
А. имеет корень, равный 6; Б. не имеет корней.
8. Решите задачу
Из двух пристаней, расстояние между которыми 57 км, навстречу друг другу вышли два катера, собственные скорости которых равны. Катер, который идет по течению реки до встречи плыл 1 час, а катер, плывший против течения – 2 часа. Найдите собственную скорость катеров, если скорость течения реки 3 км/ч.
9. Решите задачу.
Поезд прошел пути со скоростью 60 км/ч, потом задержался на 6 мин. Чтобы прибыть в конечный путь вовремя, остальной участок пути шел со скоростью 75 км/ч. Найдите расстояние, которое прошел поезд.