" Пространственные фигуры. Куб, прямоугольный параллелепипед"

Предмет: Математика

Урок:

Школа:

Дата:

ФИО учителя:

Класс:3

Количество

присутствующих:

Количество

отсутствующих:

Раздел (сквозная тема):

Раздел 3В. Пространственные фигуры

Тема урока:

Куб, прямоугольный параллелепипед.

Фотоискусство.

Цели обучения, которым посвящен урок:

3.3.2.3- изготавливать развертку пространственной геометрической фигуры (куб, прямоугольный параллелепипед) и собирать ее модель

3.3.2.4 - объяснять изменения в положении пространственных фигур, с поворотом налево, направо, вид ее сверху и сбоку

Развитие навыков:

3.2 Изображение и построение геометрических фигур

Предполагаемый результат:

Все учащиеся смогут:

изготавливать развертку пространственной геометрической фигуры

(куб, прямоугольный параллелепипед) и собирать ее модель.

Большинство учащихся смогут:

объяснять изменения в положении пространственных фигур,

с поворотом налево, направо, вид ее сверху и сбоку;

объяснять изменения в положении пространственных фигур,

с поворотом налево, направо, вид ее сверху и сбоку

Некоторые учащиеся смогут:

изготавливать развертку пространственной геометрической фигуры

(куб, прямоугольный параллелепипед) и собирать ее модель

с объяснением изменения в положении пространственных фигур,

с поворотом налево, направо, вид ее сверху и сбоку.

Языковая цель

Учащиеся могут:

объяснять, почему данная развертка является правильной или нет,

обосновывать количество граней в развертке.

Предметная лексика и терминология:

Развертка куба, изменение положения в пространстве с поворотом

налево, направо, вид ее сверху и сбоку.

Серия полезных фраз для диалога/письма

Обсуждение:

Как вы думаете, почему для изготовления разверток прямоугольного параллелепипеда нужно чертить прямоугольники?

Сколько и каких прямоугольников необходимо изобразить?

Почему их удобно расположить на листе так?

Для чего изготавливают «ушки» на развертках?

Какие фигуры являются гранями куба?

Можно ли куб назвать прямоугольным параллелепипедом и почему?

Как можно догадаться, что изображено с каждой стороны куба или прямоугольного параллелепипеда при его повороте по развертке?

Письмо:

Черчение развертки.

Материал прошедших уроков:

Прямоугольник, квадрат, куб, прямоугольный параллелепипед,

измерения фигур – длина, ширина, высота.

Ход урока:

Этапы урока

Запланированная деятельность на уроке

Ресурсы

0-3 мин

Мотивация

Педагог показывает красивые фотографии: пейзажи,

портреты, натюрморты, виды городов.

Спрашивает:

– Почему фотографию тоже можно назвать искусством?

Фотоискусство – искусство создания художественной

фотографии. Это фотографии, отражающие творческое

видение фотографа как художника.

Для фотоискусства характерно значительное

разнообразие технических средств и богатство

изобразительного языка. Фотоискусство

противопоставляется коммерческой фотографии,

которая используется для рекламы товаров и услуг.

Настрой на урок

Середина урока

4-6 мин

7-11 мин

12-29 мин

31-37 мин

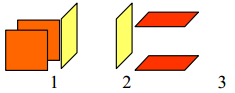
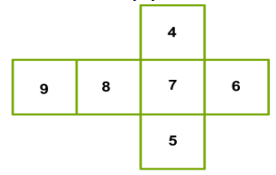
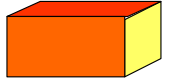
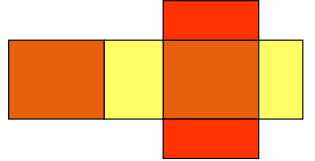
Актуализация.

Можно принести фотоаппарат и наводить его на

нужный объект либо сделать модель фотоаппарата.

Дети будут смотреть в объектив, и видеть одну из

сторон кубика.

Спрашивает у детей:

– С какой стороны надо расположить фотоаппарат,

чтобы увидеть эти грани?

Педагог показывает картинки:

1. впереди и сзади;

2. слева и справа;

3. снизу и сверху.

Педагог предлагает рассмотреть развертку. А затем

посмотреть в фотоаппарат (прямо, сверху вниз и т.д.).

– Какую грань вы увидели?

– Что на ней написано?

– Какие числа будут написаны на других гранях?

Предлагает выбрать число. Представить, что это верх

(передняя сторона, и т.д.) кубика. Назвать, что написано

снизу, слева, справа, впереди, сзади.

В действительности мы часто встречаем предметы,

имеющие похожую форму. Они могут быть сделаны из

разного материала и окрашены в разные цвета, но по

форме они напоминают друг друга. Например: коробок,

шкаф, колонки и т.д.

Эти предметы имеют похожую форму. Правда они

отличаются мелкими деталями: у колонок есть кнопки,

у шкафа – двери, но если не обращать внимания на эти

мелкие детали, то можно сказать, что все эти предметы

имеют примерно одинаковую форму. Все они

напоминают по форме изображенный на рисунке

предмет, не имеющий никаких второстепенных деталей.

– Как называют изображенное тело?

(называется прямоугольный параллелепипед).

– Оглянитесь вокруг себя.

Предлагает назвать три предмета, имеющие форму

прямоугольного параллелепипеда.

Пример ответа: тумбочка, системный блок, ящик.

Предлагает рассмотреть прямоугольный

параллелепипед.

– Ребята, что бы вы хотели узнать о прямоугольном

параллелепипеде?

Вопросы записывает на доске.

1. Чем отличается прямоугольник от прямоугольного

параллелепипеда?

2. Как найти площадь прямоугольного

параллелепипеда?

3. От какого слова произошло название

параллелепипед?

Поверхность его состоит из 6 прямоугольников,

которые называются гранями прямоугольного

параллелепипеда. Стоит запомнить, какая грань как

называется: та грань, которая обращена к нам

называется передней, точно такая же грань имеется

сзади – это задняя грань, боковые грани – левая и

правая. Та грань, которая сверху, называется верхняя, а

грань, на которой фигура стоит, называется нижней

или основанием.

Стороны граней называются ребрами, а вершины

граней – вершинами параллелепипеда.

– Посчитайте, сколько ребер у прямоугольного

параллелепипеда?

Ответ:12.

– Сколько вершин у прямоугольного параллелепипеда?

Ответ: 8.

Сколько граней у прямоугольного параллелепипеда?

Ответ: 6.

Прямоугольный параллелепипед имеет:

ребер – 12;

вершин – 8;

граней – 6.

Две грани называются противоположными, если у них

нет общего ребра.

Для противоположных граней выполняется такое же

свойство, как и для противоположных сторон

прямоугольника, именно противоположные грани

равны.

Площади противоположных граней равны.

Вывод записывают в тетради.

– Покажите противоположные грани в классной

комнате.

Постановка цели (проблемная ситуация).

Предлагает измерить длину, ширину и высоту

прямоугольного параллелепипеда.

Ответ записать в виде.

а =

в =

с =

– Мы с вами на предыдущих уроках познакомились

с прямоугольным параллелепипедом и его элементами.

Осталось нам научиться строить модель

прямоугольного параллелепипеда, а поможет нам в этом

алгоритм построения развертки параллелепипеда.

Самостоятельная работа.

Восстановить алгоритм построения развертки

параллелепипеда.

Проиллюстрировать его на бумаге и вырезать развертку.

1. Измерить длину, ширину, высоту прямоугольного

параллелепипеда. Записать, какие могут быть измерения

у прямоугольников, составляющих развертку.

2. Начертить 3 пары прямоугольников так, чтобы они не

граничили между собой (не имели общей грани) на

листе бумаги А4.

3. Сделать 3 пары «ушек» для склеивания с двух

противоположных сторон прямоугольников и еще одно

с третьей стороны одного из крайних прямоугольников.

Коррекция затруднений

Педагог проверяет правильность выполнения.

– У кого возникли затруднения?

– В каком месте вы допустили ошибку?

– В чем причина допущенной ошибки?

– Те, у кого не возникло затруднений в самостоятельной

работе, сформулируйте цель вашей деятельности.

(Выполнить дополнительные задания).

– Какова дальнейшая цель работы у тех, кто выявил

затруднения?

(Исправить ошибки).

– Используем алгоритм исправления ошибок.

– Каждый проговаривает свою учебную задачу.

Педагог предлагает задание в тетради с критериями

оценивания.

Я могу:

 объяснить изменения в положении фигур, с

поворотом налево, направо, вид ее сверху и сбоку;

 изготовить развертку геометрической фигуры

(куб, прямоугольный параллелепипед);

 собрать ее модель.

Работа над ранее изученным

Педагог дает задания индивидуально, в зависимости от

уровня продвижения ребенка.

Задача.

Сколько проволоки потребуется на изготовление

каркаса куба с ребром 10 см?

Ответ: 120 см.

Задача.

Нужно окрасить куб с ребром 5 см. Какую площадь

нужно окрасить?

Ответ: 25·6=150 см²

Самостоятельная работа.

Тест.

1. Любой прямоугольный параллелепипед состоит из

граней. Их у него:

а) 12; б) 8; в) 6.

2. У каждого прямоугольного параллелепипеда есть

ребра. Это:

а) прямоугольники; б) отрезки; в) точки.

3. Прямоугольный параллелепипед, у которого все

ребра равны, называется:

а) куб; б) прямоугольник; в) квадрат.

Ответы к тесту выводятся на экран.

1) С; 2) В; 3)А.

Задания №2, 3 нужно дать для самостоятельной работы.

Задание №7 логического характера.

Рационально вести подсчет рядами.

Есть разные варианты.

На первом рисунке, например, дети могут высчитать

сначала количество кубиков высокой стенки.

Три кубика (в одном ряду) умножить 5 рядов (15

кубиков). Затем вычислить объем оставшейся части

3∙2∙2=12

15+12=27

Другой вариант.

Вычислить объем той части, что составляет низ –

основу (3∙3∙2=18), а затем ту часть, что поставлена

сверху (3∙3=9)

18+9=27

Есть и другой рациональный способ. Дети могут

предложить «положить» торчащую часть постройки 3

на 3 сверху и посчитать объем получившегося

прямоугольного параллелепипеда 3∙3∙3=27.

Во втором случае самым рациональным будет способ:

посчитать, сколько рядов по 3 кубика в фигуре.

9 рядов по 3 кубика 3∙9=27

Задание можно усложнять.

Например, задать объем кубика: представьте, что такой

кубик 1 см³, а можно задать его сторону: представьте,

что такой кубик иммеет сторону 2 см ит.д

Учебник

Тетрадь

Тетрадь

Тетрадь

Конец урока

38-40 мин

Рефлексия.

Определяет домашнее задание с учетом

индивидуальных трудностей детей.

– Какие задачи мы ставили перед собой в начале урока?

– Удалось ли достичь этих задач?

– Возникали у вас затруднения?

– Вы смогли их преодолеть?

– Чем интересен был сегодняшний урок?

Предлагает оценить свою работу при помощи линейки

успеха.

Самооценивание

Дифференциация

Оценивание

Межпредметные

связи

В процессе работы на уроке учитель индивидуально помогает учащимся строить монологическое высказывание на заданную тему. Мотивированные дети разыгрывают ситуации общения.

Формативное оценивание.

Самооценивание в тетради «Что я знаю и умею».

Взаимооценивание при работе в паре, группе, классом.

Результаты наблюдения учителем качества ответов учащихся на уроке.

Определение уровня усвоения навыка по теме (тетрадь «Что я знаю и умею»).

– литература

– самопознание

Рефлексия для учителя:

Важные вопросы

по уроку:

Итоговая оценка (с точки зрения преподавания и обучения)

Какие два момента были наиболее успешны?

Какие два момента улучшили урок?

Что я узнал из урока о классе и отдель­ных людях, что я расскажу на следу­ющем уроке?