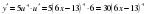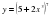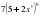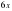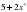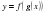Ақмола облысы
Жарқайың ауданы «Білім бөлімі» ММ
«Өмірлік орта мектебі» мемлекеттік мекемесі
Ашық сабақ
Тақырыбы: «Күрделі функцияның туындысын табу»
Сыныбы: 10
Мерзімі: 04.02.2014 жыл
Пән мұғалімі: Каримов Ерқанат Қамысбайұлы
2013 – 2014 оқу жылы
Сабақтың тақырыбы: «Күрделі функцияның туындысы»
Сабақтың мақсаттары:
а) оқушыларға күрделі функция ұғымын, оның туындысын есептеу формуласын меңгерту;
ә) ойлау жүйелілігін және талдау , салыстыра білу қабілетін дамыту;
б) іздену, бақылау арқылы оқушылардың дүние таным қабілеттерін қалыптастыру.
Құрал-жабдықтар, көрнекті құралдар: тақырып бойынша таблицалар (туынды табу ережелері, туынды табу формулалары), жаңа сабақ бойынша мысалдар, тест тапсырмалары.
Сабақтың типі: Жаңа білім беру
Сабақтың әдісі: түсіндірмелі, практикалық.
Сабақтың барысы
І.Ұйымдастыру кезеңі.Оқушыларды түгелдеп, сабаққа назарын аудару.
Сабақтың жоспарымен, бағалау шкаласымен таныстыру.
II.Үй тапсырмасын тексеру.
«С» деңгейінің №209 есебі.
Берілгені:
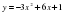 функциясы графигінің ордината осімен қиылысу нүктесі арқылы өтетін жанамасының теңдеуін жазыңдар.
функциясы графигінің ордината осімен қиылысу нүктесі арқылы өтетін жанамасының теңдеуін жазыңдар.
Шешуі:
Алдымен функцияның туындысын табамыз: 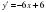 . Шыққан туындыдағы
. Шыққан туындыдағы 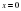 (ордината осімен қиылысуы) деп аламыз. Сонда
(ордината осімен қиылысуы) деп аламыз. Сонда 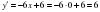 туындысын аламыз.
туындысын аламыз. 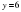 нүктесі, бұл жанаманың тангенс бұрышының ауытқу нүктесі болып табылады.
нүктесі, бұл жанаманың тангенс бұрышының ауытқу нүктесі болып табылады.
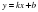 түзудің теңдеуіндегі k-ның мәні 6-ға тең. Енді бізге х=0 нүктесіндегі b – ординататысын табу ғана қалды. Ол үшін басында берілген функциядағы х=0 деп қарастырып b – ординатасын табамыз:
түзудің теңдеуіндегі k-ның мәні 6-ға тең. Енді бізге х=0 нүктесіндегі b – ординататысын табу ғана қалды. Ол үшін басында берілген функциядағы х=0 деп қарастырып b – ординатасын табамыз: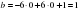 . Түзудің теңдеуіне сәйкес мәндерді қоямыз сонда біздің жанама теңдеуіміз келесі түрде болады:
. Түзудің теңдеуіне сәйкес мәндерді қоямыз сонда біздің жанама теңдеуіміз келесі түрде болады: 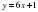
2) Қатесін тап!
| № | Функция | Функцияның туындысы | Реттік номері |
| 1 | С | k | 3 |
| 2 | х | 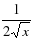
| 5 |
| 3 | kx+b | 0 | 1 |
| 4 | 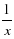
| 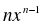
| 6 |
| 5 | 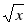
| 1 | 2 |
| 6 | 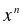
| 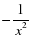
| 4 |
3)Математикалық диктант.
| № | Тапсырма мазмұны | Жауабы |
| 1 | 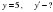
| 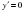
|
| 2 | 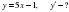
| 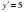
|
| 3 | 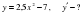
| 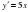
|
| 4 | 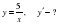
| 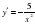
|
| 5 | 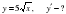
| 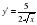
|
| 6 | 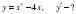
| 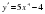
|
| 7 | 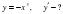
| 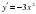
|
| 8 | 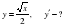
| 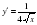
|
| 9 | 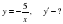
| 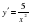
|
| 10 | Жанаманың теңдеуі | 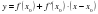
|
Орындалуын тексеру: тақтадағы есепті тексеру үшін дұрыс жауабы ілінеді.
Оқушы өзін-өзі тексереді.
Орында отырған оқушылардың жұмыстарын жинап алып тақтаға дұрыс жауабы ілінеді, бірден алған ұпайлары жарияланады.
III. Жаңа сабақ.
а) Туындының көмегімен күрделі теңдеулерді шешуге, физикада жылдамдық пен үдеуді есептеуге, геометрияда жанаманың теңдеуін анықтауға және де білімнің басқа салаларында да пайдаланылады.
Осы уақытқа дейін элементар функциялардан туынды алып үйрендік. Бүгінгі сабақта күрделі функция ұғымымен және оның туындысын есептеу формуласын пайдаланып есептер шығаруды үйренеміз.
б) y=f(x) функциясы берілсін. Оның анықталу облысы uϵU, ал функция мәндерінің жиыны Ү болсын. Айнымалы u өз кезегінде айнымалы х-ке тәуелді функция болса, яғни u=g(x), xϵX, онда y=f(g(x)) функциясы x аргументі бойынша X жиынында анықталған күрделі функция болады.
Күрделі функцияның жалпы түрі: y=f(g(x))
Күрделі функцияның туындысын табу ережесі:
Егер y=f(u) функциясының u нүктесінде, ал u=g(x) функциясының х нүктесінде туындылары бар болса, онда күрделі функцияның х аргументі бойынша туындысы бар болып және ол туынды
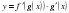 (1)
(1)
формуласымен анықталады.
y= f(g(x)) күрделі функцияның жалпы түрі u=g(x) күрделі функцияның ішкі бөлігі, ал y=f(u) сыртқы бөлігі деуге болады.
Енді күрделі функцияның ішкі және сыртқы бөлігін ажыратуға бірнеше мысал келтірейік: y=f(u), u=g(x)
1-мысал.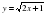 -күрделі функция. Себебі,
-күрделі функция. Себебі, 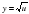 фунцияның сыртқы бөлігі, u= 2х+1 функцияның ішкі бөлігі.
фунцияның сыртқы бөлігі, u= 2х+1 функцияның ішкі бөлігі.
2-мысал.  және
және 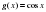 функцияларынан
функцияларынан 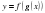 және
және 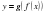 күрделі функцияларды құрастырайық.
күрделі функцияларды құрастырайық.
Күрделі функцияның туындысытабу ережесі: 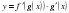
Осы формуланы пайдалануға мысал келтірейік:
3-мысал. 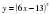 функциясының туындысын табайық. Мұнда
функциясының туындысын табайық. Мұнда 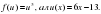 Онда
Онда 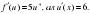 Ендеше (1) формула бойынша
Ендеше (1) формула бойынша 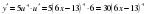
ІV.Жаңа сабақты бекіту. Күрделі функцияның туындысын табу жұмыртқаның бөліктері ретінде қарастырып, сыртқы бөлігінен туынды алу, «қабығын ашу» ретінде қарастыру бірақ ақ уызы алынып, сары уызы өзгеріссіз қалады, яғни:
| Жұмыртқа | Қабығын ажыратып тастау нәтижесі | Ақ уызын алып тастау нәтижесі | Сары уызы |
| 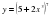
| 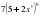
| 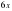
| 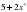
|
| 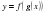
| 
| 
| 
|
V Жаттығу есептерін шығару
№213 (а, б); №214 (а, б); №216 (а, б); №217 (а, б); №220 (а, б)
№213 Күрделі функциясын құрайтын функцияларды анықта:
a) 
б)
№214 Элементар функциялардан тұратын күрделі функция жазу керек:
а) 
б) 
№216 Функцияның туындысын тап:
а) 
б) 

№217 Функцияның туындысын тап:
а)
б)
№220 Функцияның туындысын тап:
а)
б)
VI. Тест алу
1. Функцияның туындысын табыңыз: 
А)  В)
В)  С)
С)  Д)
Д)  Е)
Е) 
2.  функциясы берілген.
функциясы берілген.  табыңыз
табыңыз
А)  В)
В)  С)
С)  Д)
Д)  Е)
Е) 
3.  функциясының туындысын табыңыз
функциясының туындысын табыңыз
А) В)
В)  С)
С)  Д)
Д)  Е) 1
Е) 1
4. Функцияның туындысын табыңыз: 
А) В)
В)  С)
С)  Д)
Д)  Е)
Е) 
5.  функциясының туындысын табыңыз
функциясының туындысын табыңыз
А)  В)
В)  С)
С)  Д)
Д)  Е)
Е) 
Дұрыс жауаптары: 1.А 2.В 3.В 4.С 5.Д
VII.Қорытынды.
а) Күрделі функцияның туындысын қандай ереже бойынша аламыз?
ә)есеп шығаруда қандай ереже жиі пайдаланылды?
VIII. Үйгетапсырма: №213-216-220 (ә,в)
IX.Бағалау.
Бағалау шкаласы
13-15 -«5»
9-11- «4»
5-8 -«3»
Математикалық диктант-2есеп -1ұпай
Жаңа сабақ бойынша есеп-1 есеп -1 ұпай
Тест-1 есеп -1 ұпай
Қосымша 1
Үлгермеуші оқушылармен жұмыс
1-карточка
1-тапсырма . Туындыны есепте 
2-тапсырма.  функциясының туындысын есепте
функциясының туындысын есепте
3-тапсырма . 
2-карточка
1-тапсырма . Туындыны есепте 
2-тапсырма.  функциясының туындысын есепте
функциясының туындысын есепте
3-тапсырма . 
3-карточка
1-тапсырма . Туындыны есепте 
2-тапсырма.  функциясының туындысын есепте
функциясының туындысын есепте
3-тапсырма . 
4-карточка
1-тапсырма . Туындыны есепте 
2-тапсырма.  функциясының туындысын есепте
функциясының туындысын есепте
3-тапсырма . 
Қосымша 2
Оқушылардың бағалау парағы
| № | Оқушының аты-жөні:________________________________ | Ұпай саны |
| 1 | Математикалық диктант-2есеп -1ұпай
|
|
| 2 | Жаңа сабақ бойынша есеп-1 есеп -1 ұпай
|
|
| 3 | Тест-1 есеп -1 ұпай
|
|
| 4 | Жалпы ұпайлар саны және алған бағасы: |
|
Бағалау шкаласы: 13-15 -«5» 9-11- «4» 5-8 -«3»
| № | Оқушының аты-жөні:________________________________ | Ұпай саны |
| 1 | Математикалық диктант-2есеп -1ұпай
|
|
| 2 | Жаңа сабақ бойынша есеп-1 есеп -1 ұпай
|
|
| 3 | Тест-1 есеп -1 ұпай
|
|
| 4 | Жалпы ұпайлар саны және алған бағасы: |
|
Бағалау шкаласы: 13-15 -«5» 9-11- «4» 5-8 -«3»
| № | Оқушының аты-жөні:________________________________ | Ұпай саны |
| 1 | Математикалық диктант-2есеп -1ұпай
|
|
| 2 | Жаңа сабақ бойынша есеп-1 есеп -1 ұпай
|
|
| 3 | Тест-1 есеп -1 ұпай
|
|
| 4 | Жалпы ұпайлар саны және алған бағасы: |
|
Бағалау шкаласы: 13-15 -«5» 9-11- «4» 5-8 -«3»

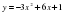
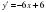
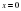 (ордината осімен қиылысуы) деп аламыз. Сонда
(ордината осімен қиылысуы) деп аламыз. Сонда 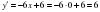 туындысын аламыз.
туындысын аламыз. 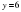 нүктесі, бұл жанаманың тангенс бұрышының ауытқу нүктесі болып табылады.
нүктесі, бұл жанаманың тангенс бұрышының ауытқу нүктесі болып табылады. 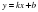
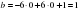
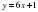
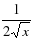
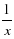
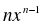
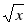
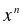
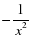
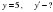
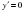
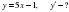
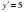
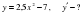
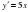
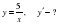
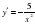
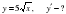
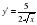
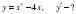
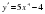
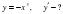
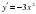
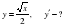
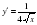
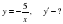
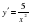
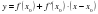
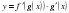
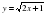 -күрделі функция. Себебі,
-күрделі функция. Себебі, 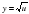 фунцияның сыртқы бөлігі,
фунцияның сыртқы бөлігі,  және
және 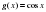 функцияларынан
функцияларынан 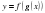 және
және 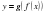 күрделі функцияларды құрастырайық.
күрделі функцияларды құрастырайық. 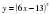 функциясының туындысын табайық. Мұнда
функциясының туындысын табайық. Мұнда 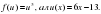 Онда
Онда 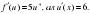 Ендеше (1) формула бойынша
Ендеше (1) формула бойынша