Презентация для урока "Производная сложной функций"

Тип урока: урок изучения нового материала

Вид урока: урок-экскурсия

Методы и приёмы: информационный, частично-поисковый, взаимообучения, метод ошибок, словесный, наглядный.

Формы работы: индивидуальная, групповая, коллективная, устная, письменная.

Цели урока:

Образовательные:

ü Сформировать у учащихся понятие сложной функции.

ü Изучить алгоритм вычисления производной сложной функции;

Показать его применение при вычислении производных.

ü Научить выполнять простейшие задания на применение правила дифференцирования сложной функции.

Развивающие:

ü Продолжить развитие умений логически и аргументировано рассуждать, используя обобщения, анализ, сравнение при изучении производной сложной функции.

ü Способствовать развитию умений осуществлять самоконтроль, самооценку и самокоррекцию.

Воспитательные:

Воспитывать наблюдательность в ходе отыскания математических зависимостей, продолжить формирование самооценки при осуществлении дифференцированного обучения, повышать интерес к математике.

ü Воспитание познавательной активности, воспитать у учащихся любовь и уважение к предмету, научить видеть в ней не только строгость, сложность, но и логичность, простоту и красоту.

ü Воспитание любви к Родине.

Ожидаемые результаты: учащиеся должны иметь представление о сложной функции и правилах ее дифференцирования, уметь выполнять простейшие задания на применение правила дифференцирования сложной функции.

Используемые учебники и учебные пособия:

ü Алгебра и начала анализа. Учебник для 10-11 классов общеобразовательных учреждений под ред. А.Е. Абылкасымовой;

ü Алгебра и начала анализа. Учебник для 10-11 классов общеобразовательных учреждений под ред. А.Н.Колмогорова.

Используемое оборудование: компьютер, мультимедийная установка.

Используемые ЦОР:

Мультимедийная презентация учителя "Производная сложной функции", тесты, подготовленные средствами MS PowerPoint, карточки для индивидуальной работы.

План урока:

I. Организация начала урока.

II. Проверка выполнения домашнего задания.

III. Актуализация опорных знаний и умений.

IV. Усвоение новых знаний.

V. Первичная проверка понимания учащимися учебного нового материала.

VI. Закрепление знаний.

VII. Контроль и самоконтроль знаний.

VIII. Задание на дом.

IX. Оценка знаний.

X. Подведение итогов урока.

Ход урока:

I. Организация начала урока. Формулировка темы урока и постановка целей. (2 мин)

(Слайд 1,2)

Здравствуйте, ребята! Садитесь, пожалуйста. Сегодня у нас с вами необычный урок. Тема урока "Производная сложной функции". Я надеюсь, что этот урок пройдет интересно, с большой пользой для всех. Мне бы хотелось взять эпиграфом к нашему уроку высказывание

(Слайд 3)

Эпиграф:
«Кто хочет ограничиться настоящим без знания прошлого, тот никогда его не поймет».

Готфрид Вильгельм Лейбниц

Значит, на уроке нам необходимы знания прошлых уроков.

У вас на столе лежат различные задания и лист оценивания. Внесите туда свою фамилию. Все достигнутые результаты вы будете заносить в таблицу, после чего подсчитаете баллы и оцените себя.

Сегодня на уроке мы повторим понятие производной, правила вычисления производных, научимся находить производную сложной функции.

Открываем тетради, записываем число и тему урока. Урок у нас с вами будет необычный потому, что отправимся мы сегодня в путешествие. А куда? Узнаем, если проверим ваше домашнее задание.

II. Проверка домашнего задания. (Слайд 4)

Вы дома вычисляли производные функции.

Теперь сопоставьте свой ответ с буквой на листке тестов и составьте предложение.

Итак, получилось слово "КОКШЕТАУ".

И сегодня на уроке мы не только изучим новую тему, но и проследим основные этапы жизни нашего города Кокшетау.

III. Актуализация опорных знаний и умений.

Проверим знание определений, формул и правил.

Устно: Вставьте пропущенные слова.

1)Производной функции в точке называется число, к которому стремится отношение (приращения функции к приращению аргумента)

2) Нахождение производной функции f называется (дифференцированием).

3) Производная суммы равна (сумме производных).

4) Постоянный множитель можно выносить за знак производной.

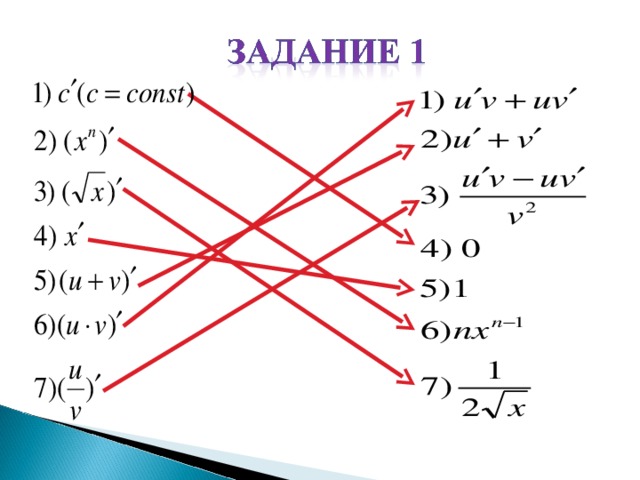
Задание1.

Вам предлагается карточка, в которой работая в паре, для каждой формулы вы должны найти ответ, соединив их стрелкой. (слайд 7)

Задание 2.

Найдите производные функции: (слайд 8)

Группа Cтепень (основан 1824г. как военное укрепление Кокчетав)

Группа Теорема (статус города Кокчетав приобрел в 1862г)

Группа Константа

В 1993г Постановлением Президиума Верховного Совета Республики Казахстан город Кокчетав был переименован в Кокшетау

Сейчас мы выясним, как называются функции под номерами 5, как вычисляются их производные.

IV. Усвоение новых знаний

Сложная функция — это функция от функции. Если g — функция от x, то есть g=g(x), а f — функция от g: f=f(g), то функция h=f(g) — сложная. А g в этом случае называют промежуточным аргументом. Еще часто f называют внешней функцией, а g — внутренней. Лучший способ понять, что такое сложная функция — рассмотреть примеры сложных функций.

Если h=f(g), где g=g(x), то есть h — сложная функция, то производная сложной функции находится по следующему правилу: h’=f’(g(x))·g’(x), то есть производную внешней функции g надо умножить на производную внутренней функции f.

Примеры.

Итак, мы выяснили, что такое сложная функция.

Алгоритм вычисления сложной функции h(x) = f(g(x)).

определить внешнюю функцию f(g)
найти производную внешней функции f'(g)
определить внутреннюю функцию g(x).

4) найти производную внутренней функции g'(x)

найти произведение производной внутренней на производную внешней функции f’(g(x))·g’(x).

Каждому дается памятника с алгоритмом.

Примеры.

V.Первичная проверка понимания учащимися учебного нового материала.

Задание 3.

Задайте формулами элементарные функции f и g, из которых составлена сложная функция h(x)=f(g(x))

Ответы:

Задание 4. Перед вами 5 решённых примеров, среди которых есть правильные, остальные с ошибкой. Определите правильный пример (назовите его номер), в остальных исправьте ошибки.

Получаем, примеры, с номерами 1, 4, 5

Численность населения Кокшетау 154 тыс.человек

Решение записывают в тетради, номера правильных ответов записывают в оценочный лист.

VI. Закрепление знаний.

Задание 5 (Работа у доски по учебнику).

№ 154

VII. Контроль и самоконтроль знаний.

Задание 6

Тесты (индивидуально).

Вам предлагается за определённое время решить небольшой тест. Запишите ответы в оценочный лист. Сопоставьте полученные ответы буквам и прочтите зашифрованное слово.(слайд 13)

Какое слово у вас получилось? Бурабай

VIII. Задание на дом.

(Слайд 15)

Группы Степень и Теорема: Стр. 107 № 157

Группа Константа: стр.107 № 157, стр. 150 № 3

IX. Оценка знаний.

Заполнение оценочного листа, выставление оценок.

X. Подведение итогов урока.

С помощью слайдов, созданных в программе Power Point, мы выполнили большой объем работы, повторили теорию, решали различные задания, выполняли устные упражнения, провели самопроверку, получили возможность самостоятельной деятельности, ознакомились с достопримечательностями Кокшетау и статистическими данными.

Вот и подошел к концу наш урок. Тест и вычисления показали, что большинство из вас поняли новый учебный материал. Я довольна вашими результатами и вашей работой в группах. (Слайд 17)

Рефлексия.

Спасибо за урок!

Производная сложной функции

Оценочный лист учащегося

Группа________

Фамилия____________________________________

Имя________________________________________

Этапы

Задания

Количество баллов

Проверка домашнего задания

(СЛОВО______________)