Урок-расследование.
Тема урока: «Производная»
Цель урока: выяснить степень готовности учащихся по теме «Производная». Обобщить знания по теме.
Задачи урока:
Систематизация знаний учащихся по теме «Производная ».
Развитие мыслительной деятельности.
Воспитание умений работать в команде.
Ход урока.
1. Оформление доски (записи темы)
2. Организационный момент.
3. Цель и задачи урока.
4. Проверка домашней работы — опрос формул и правил. Трое учащихся записывают их на доске.
5. Устные упражнения для всех учащихся.
Найти производную. Ответы. 1) 2x-3 1) 2 2) x² -2 2) 2x 3) 3x²-6x 3) 6x-6 4) (x-3)4 4) 4(x-3)³
5) (2x+1)² 5) 4(2x+1) 6) 3cosx 6) -3sinx
7) cos5x 7) -5sin5x
8) 2sinx 8) 2cosx
9) sin2x 9) 2cos2x
10) 5tgx 10) 5/cos²x
11) tg3x 11) 3/cos²3x
12) ctg2x 12) -2/sin²2x
13) 2ctg3x 13) -6/sin²3x
6) Проверка домашней работы и выставление оценок.
7) Программированный контроль (10 мин.)
Задание Варианты ответов
| IB | IIB | 1 | 2 | 3 | 4 |
| 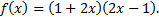 Найдите �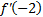 � � | 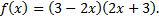 Найдите �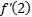 � � | -16 | 17 | 16 | -17 |
| 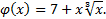 Найдите �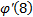 � � | 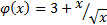 Найдите �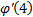 � � | 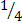 | 2� � � | 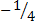 | 1 |
| 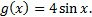 Найдите �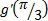 � � | 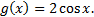 Найдите �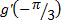 � � | -2 | 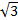 | 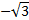 | 2 |
| �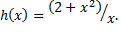 � Найдите� � Найдите�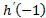 � � | �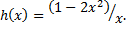 � Найдите� � Найдите�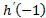 � � | 3 | 1 | -1 | -3 |
Проверка этого задания в парах.
Верный ответ: I в. - 1,2,4,3.
II в. - 3,1,2,4.
Устная или письменная работа по устранению ошибок учащихся.
Полученные правильные ответы являются кодом для нашего расследования.
8) Учащиеся садятся в группы по 6 человек.
Каждая группа получает карточку с заданием и таблицу ответов.
№1
1) Найдите f'(5), если f(x)= 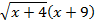
2) Найдите f'(x)0, если f(x)= 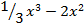
3) Решите уравнение f'(x)=0, f(x)=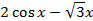
4) f(x)=2sin3x. Найдите f' 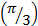
№2
1) Решите уравнение f'(x)=0, если f(x)=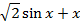
2)Решите неравенство f'(x)0, если f(x)=(4/3)x³-8x²
3) Найдите f'(п/2), если f(x)=3sin2x
4) Найдите f'(6), если f(x)=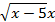
№3
1)Решите уравнение f'(x)=0, f(x)=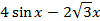
2) Найдите f'(п/6), если f(x)=4cos5x
3) Найдите f'(4), если f(x)= 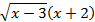
4) Решите неравенство f'(x)0, если f(x)=4x³-3x²
№4
1) Найдите f'(3), если f(x)=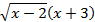
2) Решите неравенство f'(x)0, если f(x)=x³-6x²
3) Найдите f'(п/2), если f(x)=5cos4x
4) Решите уравнение f'(x)=0, если f(x)=cosx-x
Таблица ответов:
Группа с карточкой №1 и №3 решают по коду I варианта, а группы с карточками №2 и №4 решают по коду II варианта.
| 1 | 4 (е) | 11 | �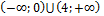 �(д) �(д) |
| 2 | 8 (у) | 12 | �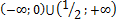 � (п) � (п) |
| 3 | -6 (а) | 13 | �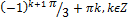 �(ч) �(ч) |
| 4 | -20 (в) | 14 | �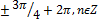 � (ж) � (ж) |
| 5 | 0 (р) | 15 | �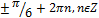 � (m) � (m) |
| 6 | -4 (к) | 16 | �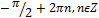 � (и) � (и) |
| 7 | -10 (н) | 17 | �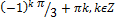 � (м) � (м) |
| 8 | 5 (я) | 18 | �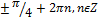 � (0) � (0) |
| 9 | (0;�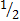 �) (б) �) (б) | 19 | �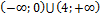 � (с) � (с) |
| 10 | (0;4) (г) | 20 | �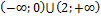 � (з) � (з) |
9) Одновременно с этим к доске выходят учащиеся по карточкам с подобными заданиями.
№1
Найдите f'(6), если f(x)=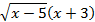
№2
Решите неравенство f'(x)0, если f(x)= (1/4)x4-2x³.
№3
Решите уравнение f'(x)=0, f(x)=2cosx+x
№4
Найдите f'(п/6), если f(x)=4cos3x
После решения своей карточки учащиеся получают оценки и садятся в свои группы и присоединяются к решению.
10) После того как каждая группа решила свои задания, она получила шифр. Этот шифр записывается на доске
I к. - У Д А Ч
II к. - А Ж Д Е
III к. - Т В П Е
IV к. - Р Е Д И
И если все команды решили верно, то в результате получится фраза:
«Удача ждет впереди»
11) А теперь, ребята, посмотрим, кому сегодня улыбнется удача.
Упражнения с дифференцированным подходом.
а) f'(x)/g'(x)≥0, если f(x)=x³-3x
g(x)=x²-6x
б) h'(x)h(x)=(1/4)x4-x³-x²+6x+1997
в) f'(x)f(x)=(2x+1)/(x-2)²
“5” - любые 2 задания
“4” - любое 1 задание
“3” - найти производную в б) и в)
12) Итог урока
13) Домашнее задание к контрольной работе по теме «Производная».
















