ПрактическАЯ РАБОТА№ 8
Тема: Механический смысл производной
Цели:
- повторить, в чем заключается механический смысл производной
- рассмотреть решение примеров на механический смысл производной
Оснащение занятия: конспект лекций.
Критерии оценок
оценка «5» ставится за правильные ответы на все вопросы и верное выполнение всех заданий работы
оценка «4» ставится за правильные ответы на все вопросы и верное выполнение любых шести заданий работы
оценка «3» ставится за правильные ответы на вопросы и верное выполнение любых пяти заданий работы
Порядок выполнения работы
Задание 1.
- Ознакомиться с лекцией № 8
- Пользуясь лекциями, ответить на вопросы и ответы записать в тетрадь:
1. В чем заключается механический смысл производной?
2. Как находится скорость движения материальной точки?
3. Как вычисляется ускорение с помощью производной
Лекция 8.
Тема «Механические приложения производной»
Производная от функции y = y(x), вычисленная при значении аргумента х = х0, представляет собой скорость изменения этой функции относительно независимой переменной х в точке х = х0.
В частности, если зависимость между пройденным путем s и временем t при прямолинейном движении выражается формулой s = s(t), то скорость движения в любой момент времени t есть (т. е. скорость изменения скорости) есть
Пример.
1. Точка движется прямолинейно по закону s = (s выражается в метрах, - в секундах). Найти скорость и ускорение движения через 1 с после начала движения.
Решение:
Скорость прямолинейного движения равна производной пути по времени:
v(t) = =, откуда v(1) = 4 (м/с)
Ускорение прямолинейного движения равно второй производной пути по времени: a(t) = = 2t + 4.
Следовательно, a(1) = 6(м/с2)
Задание 2. Решить предложенные примеры
Решить самостоятельно следующие задачи:
2. Закон прямолинейного движения точки выражается формулой
s = 1 + (s выражается в метрах, - в секундах). Найти скорость и ускорение движения в момент времени
3. Тело массой 25 кг движется прямолинейно по закону s = ln(1 + Найти кинетическую энергию тела (0.5m через 2с после начала движения.
4. Точка движется по оси абсцисс по закону x = 0,25(
(х выражается в метрах, - в секундах). В какой момент времени точка остановится?
5. Точка движется прямолинейно по закону s(t) = 4 +4 (s измеряется в метрах, t – в секундах). Напишите формулы, выражающие скорость и ускорение в любой момент времени и вычислите их при t = 3с.
6. Материальная точка движется по прямой согласно уравнению
s(t) = + 3t. Найдите, в какой момент времени ускорение будет равно нулю и вычислите скорость в этот момент времени.
7. Маховик, задерживаемый тормозом, поворачивается за t секунд на угол α = 2t – 0,04(рад). Определите угловую скорость вращения маховика в момент t = 12с и выяснить, в какой момент маховик остановится.
8. Материальная точка движется прямолинейно
ПрактическАЯ РАБОТА№ 8
Тема: Механический смысл производной
Цели:
- повторить, в чем заключается механический смысл производной
- рассмотреть решение примеров на механический смысл производной
Оснащение занятия: конспект лекций.
Критерии оценок
оценка «5» ставится за правильные ответы на все вопросы и верное выполнение всех заданий работы
оценка «4» ставится за правильные ответы на все вопросы и верное выполнение любых шести заданий работы
оценка «3» ставится за правильные ответы на вопросы и верное выполнение любых пяти заданий работы
Порядок выполнения работы
Задание 1.
- Ознакомиться с лекцией № 8
- Пользуясь лекциями, ответить на вопросы и ответы записать в тетрадь:
1. В чем заключается механический смысл производной?
2. Как находится скорость движения материальной точки?
3. Как вычисляется ускорение с помощью производной
Лекция 8.
Тема «Механические приложения производной»
Производная от функции y = y(x), вычисленная при значении аргумента х = х0, представляет собой скорость изменения этой функции относительно независимой переменной х в точке х = х0.
В частности, если зависимость между пройденным путем s и временем t при прямолинейном движении выражается формулой s = s(t), то скорость движения в любой момент времени t есть (т. е. скорость изменения скорости) есть
Пример.
1. Точка движется прямолинейно по закону s = (s выражается в метрах, - в секундах). Найти скорость и ускорение движения через 1 с после начала движения.
Решение:
Скорость прямолинейного движения равна производной пути по времени:
v(t) = =, откуда v(1) = 4 (м/с)
Ускорение прямолинейного движения равно второй производной пути по времени: a(t) = = 2t + 4.
Следовательно, a(1) = 6(м/с2)
Задание 2. Решить предложенные примеры
Решить самостоятельно следующие задачи:
2. Закон прямолинейного движения точки выражается формулой
s = 1 + (s выражается в метрах, - в секундах). Найти скорость и ускорение движения в момент времени
3. Тело массой 25 кг движется прямолинейно по закону s = ln(1 + Найти кинетическую энергию тела (0.5m через 2с после начала движения.
4. Точка движется по оси абсцисс по закону x = 0,25(
(х выражается в метрах, - в секундах). В какой момент времени точка остановится?
5. Точка движется прямолинейно по закону s(t) = 4 +4 (s измеряется в метрах, t – в секундах). Напишите формулы, выражающие скорость и ускорение в любой момент времени и вычислите их при t = 3с.
6. Материальная точка движется по прямой согласно уравнению
s(t) = + 3t. Найдите, в какой момент времени ускорение будет равно нулю и вычислите скорость в этот момент времени.
7. Маховик, задерживаемый тормозом, поворачивается за t секунд на угол α = 2t – 0,04(рад). Определите угловую скорость вращения маховика в момент t = 12с и выяснить, в какой момент маховик остановится.
8. Материальная точка движется прямолинейно
ПрактическАЯ РАБОТА№ 8
Тема: Механический смысл производной
Цели:
- повторить, в чем заключается механический смысл производной
- рассмотреть решение примеров на механический смысл производной
Оснащение занятия: конспект лекций.
Критерии оценок
оценка «5» ставится за правильные ответы на все вопросы и верное выполнение всех заданий работы
оценка «4» ставится за правильные ответы на все вопросы и верное выполнение любых шести заданий работы
оценка «3» ставится за правильные ответы на вопросы и верное выполнение любых пяти заданий работы
Порядок выполнения работы
Задание 1.
- Ознакомиться с лекцией № 8
- Пользуясь лекциями, ответить на вопросы и ответы записать в тетрадь:
1. В чем заключается механический смысл производной?
2. Как находится скорость движения материальной точки?
3. Как вычисляется ускорение с помощью производной
Лекция 8.
Тема «Механические приложения производной»
Производная от функции y = y(x), вычисленная при значении аргумента х = х0, представляет собой скорость изменения этой функции относительно независимой переменной х в точке х = х0.
В частности, если зависимость между пройденным путем s и временем t при прямолинейном движении выражается формулой s = s(t), то скорость движения в любой момент времени t есть (т. е. скорость изменения скорости) есть
Пример.
1. Точка движется прямолинейно по закону s = (s выражается в метрах, - в секундах). Найти скорость и ускорение движения через 1 с после начала движения.
Решение:
Скорость прямолинейного движения равна производной пути по времени:
v(t) = =, откуда v(1) = 4 (м/с)
Ускорение прямолинейного движения равно второй производной пути по времени: a(t) = = 2t + 4.
Следовательно, a(1) = 6(м/с2)
Задание 2. Решить предложенные примеры
Решить самостоятельно следующие задачи:
2. Закон прямолинейного движения точки выражается формулой
s = 1 + (s выражается в метрах, - в секундах). Найти скорость и ускорение движения в момент времени
3. Тело массой 25 кг движется прямолинейно по закону s = ln(1 + Найти кинетическую энергию тела (0.5m через 2с после начала движения.
4. Точка движется по оси абсцисс по закону x = 0,25(
(х выражается в метрах, - в секундах). В какой момент времени точка остановится?
5. Точка движется прямолинейно по закону s(t) = 4 +4 (s измеряется в метрах, t – в секундах). Напишите формулы, выражающие скорость и ускорение в любой момент времени и вычислите их при t = 3с.
6. Материальная точка движется по прямой согласно уравнению
s(t) = + 3t. Найдите, в какой момент времени ускорение будет равно нулю и вычислите скорость в этот момент времени.
7. Маховик, задерживаемый тормозом, поворачивается за t секунд на угол α = 2t – 0,04(рад). Определите угловую скорость вращения маховика в момент t = 12с и выяснить, в какой момент маховик остановится.
8. Материальная точка движется прямолинейно
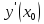 от функции y = y(x), вычисленная при значении аргумента х = х0, представляет собой скорость изменения этой функции относительно независимой переменной х в точке х = х0.
от функции y = y(x), вычисленная при значении аргумента х = х0, представляет собой скорость изменения этой функции относительно независимой переменной х в точке х = х0. 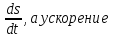 (т. е. скорость изменения скорости) есть
(т. е. скорость изменения скорости) есть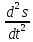
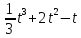 (s выражается в метрах,
(s выражается в метрах, 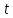 - в секундах). Найти скорость и ускорение движения через 1 с после начала движения.
- в секундах). Найти скорость и ускорение движения через 1 с после начала движения. 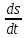 =
= 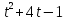 , откуда v(1) = 4 (м/с)
, откуда v(1) = 4 (м/с)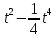 (s выражается в метрах,
(s выражается в метрах, 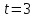
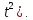 Найти кинетическую энергию тела (0.5m
Найти кинетическую энергию тела (0.5m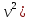 через 2с после начала движения.
через 2с после начала движения.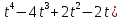
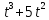 +4 (s измеряется в метрах, t – в секундах). Напишите формулы, выражающие скорость и ускорение в любой момент времени и вычислите их при t = 3с.
+4 (s измеряется в метрах, t – в секундах). Напишите формулы, выражающие скорость и ускорение в любой момент времени и вычислите их при t = 3с.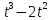 + 3t. Найдите, в какой момент времени ускорение будет равно нулю и вычислите скорость в этот момент времени.
+ 3t. Найдите, в какой момент времени ускорение будет равно нулю и вычислите скорость в этот момент времени.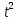 (рад). Определите угловую скорость вращения маховика в момент t = 12с и выяснить, в какой момент маховик остановится.
(рад). Определите угловую скорость вращения маховика в момент t = 12с и выяснить, в какой момент маховик остановится.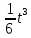 +
+ 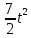 – t, (s измеряется в метрах, t – в секундах). Найдите момент времени, когда ускорение точки будет равно нулю и скорость, с какой движется точка в этот момент времени.
– t, (s измеряется в метрах, t – в секундах). Найдите момент времени, когда ускорение точки будет равно нулю и скорость, с какой движется точка в этот момент времени.















