Урок: Использование формул в решении уравнения.
Цель урока: изучить особенности применения формул в решении уравнений, получить механизм оценки, когда использование математической формулы, может приводить к потере корней или к приобретению посторонних корней.
Ход урока
Тема Использование формул в решении уравнений
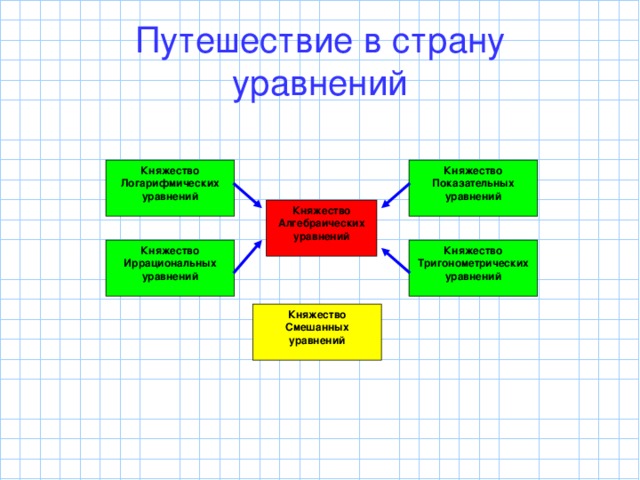
Вступление: Сегодня ребята мы совершим с вами путешествие в удивительную страну - страну уравнений. Это государство состоит из отдельных княжеств и живут в них удивительные люди формулы, законы, определения. Давайте же поближе познакомимся с княжествами этого государства.
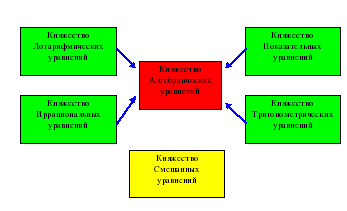
Самым древним и самым могущественным является княжество Алгебраических уравнений, возраст его жителей - не одно тысячелетие, и наполнялось оно своими обитателями мучительно и долго. Многие великие математики участвовали в его создании, результатом их открытий стали формулы решения базовых уравнений, с некоторыми жителями этого княжества вы уже хорошо знакомы это уравнения первой степени ( линейные) и второй степени (квадратные).
Уравнения первой степени решали еще в древнем Вавилоне, правда они решали их довольно сложным спсообом, похожим на решение системы по теореме Виета,
Евклид решал квадратные уравнения с помощью геометрических соображне
Аль-хорезми впервые начал решать задачи с помощью формул, похожих на теми какими пользуемся мы.
Но не только знакомые жители живут в этом государстве, 6 веков понадобилось человечеству чтобы появился новый житель этого княжества формула корня кубического уравнения и заслуга в этом усилие Итальянских математиков Кардано, Тарталье и Ферро. Существует бесконечное множество уравнений и если бы математики искали для каждого свое решение, то математика наверно бы утонула в бесконечности этих формул, государство формул было бы перенаселено, и нам было бы очень трудно найти решение. Понятно, что такой подход не является продуктивным. Математики сосредоточили свои усилия на решение базовых уравнений, к которым сводятся другие уравнения данного класса. Выпишем базовые уравнения и формулы их корней.
Уравнения первой степени – метод решения переносы известных и неизвестных слагаемых
Уравнение второй степени вида 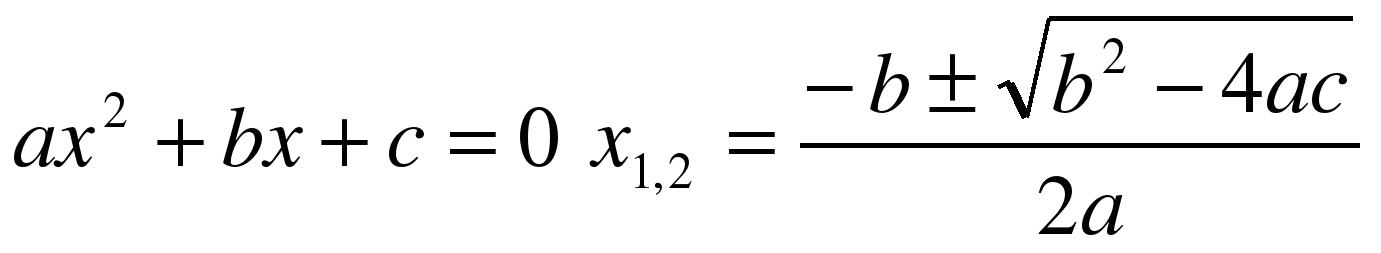
Уравнения третьей степени вида 
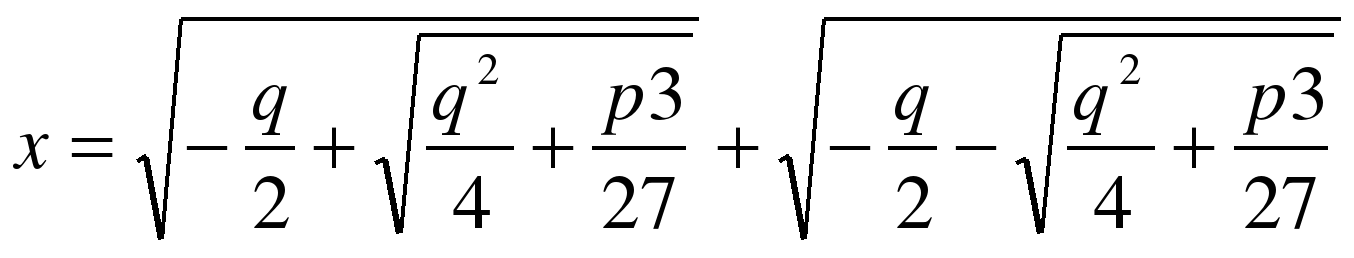 Открыты в 16 веке, Кардано, Тарталье и Ферро. Один корень может быть найден по этой формуле, остальные могут быть отделены с помощью теоремы Безу.
Открыты в 16 веке, Кардано, Тарталье и Ферро. Один корень может быть найден по этой формуле, остальные могут быть отделены с помощью теоремы Безу.
Уравнения, которые могут быть сведены к произведению многочленов первой и второй степени.
Каждый путешественник, заезжает в эту страну не просто так, он приходит со своим уравнением. Если это уравнение имеет базовый вид, его сразу направляют к формулам получения корней и благодарный путник получает свое сокровище, он получает решение уравнения. Но чтобы получить решение, надо точно знать, действительно ли полученный результат является решением.
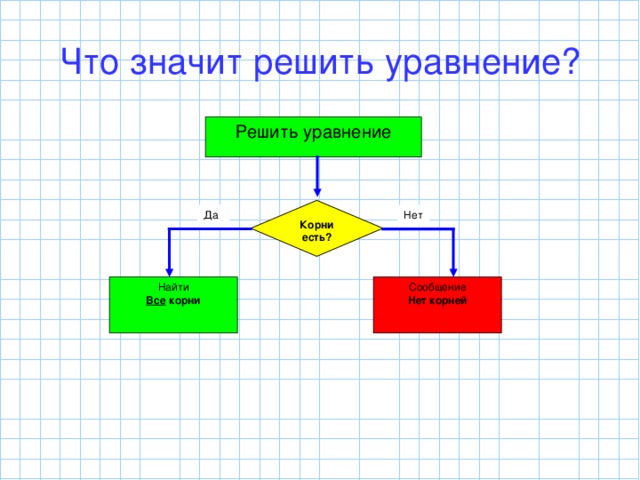
Вопрос что значит решить уравнение? Обсуждается ответы учеников, в конце на доске записывается блок-схема.
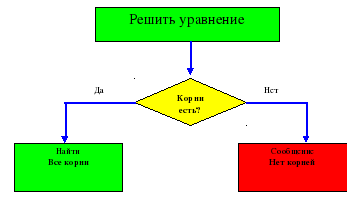
В каждом княжестве живут формулы и здесь принято дружелюбное и вежливое общение, поэтому в этой стране принято к ее жителям обращаться по именам. Давайте зайдем в каждое княжество и обратимся к его обитателям. Я начинаю, а вы ребята продолжаете в своих тетрадях, а потом формулы выписываются на доске и обсуждаются, где формулы, где определение, где формулы корней. Итак, страна формул начала наполняться своими обитателями. А теперь внимательно посмотрим на получившиеся формулы, какие-то выполнены в виде переходов, а какие-то в виде равенств.
Первые - это коренные жители этой страны, они позволяют получать корни или сводить уравнение к алгебраическому, Здесь мы видим, что формулы корней уравнения помогают нам получить решение уравнения, не задумываясь как они получены, они выполняют работу, которая однажды уже проделана и мы используем эти результаты, что сокращает затраченное время и избавляет нас от необходимости всякий раз заново проводить эти вычисления.
А другие выполнены в виде равенств состоящих из левой и правой части. Эти жители пришли в эту страну из страны вычислений и они берут какую-то часть уравнения и ее преобразуют.
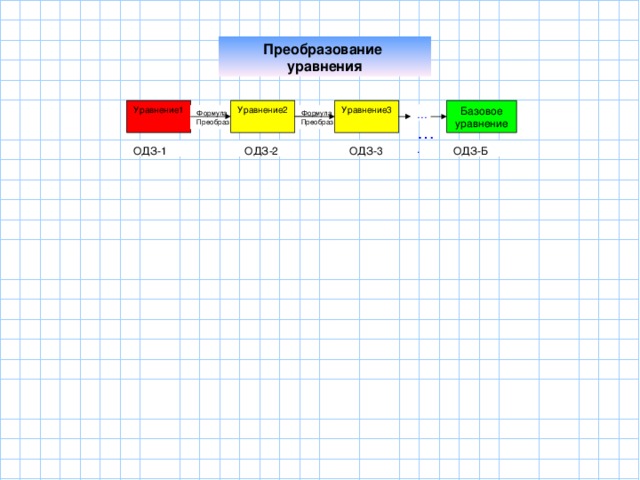
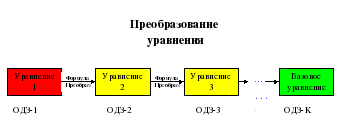
Демонстрируется слайд перехода между одним уравнением к другому.


Так продвигаясь шаг за шагом по дороге преобразований, мы приближаемся к базовому уравнению, случается что путешественники и заходят в тупик или находят не то что искали или находят не все что хотели или ложные решения. Историю этих путешествий хранят жители это государства, вот послушайте некоторые.
Это путешествие было короткое, путник направился в княжество логарифмических уравнений. Вот его хронология.
log3(x-2)2=2
2 log3(x-2)=2
log3(x-2)=1 (Базовое уравнение)
x-2=3
x=5
Он сделал проверку все получилось.
Второе путешествие было в страну Иррациональных уравнений, здесь путешественник применил известную формулу и сразу встал в тупик, уравнение было простым и он сразу остановился в недоумении, в чем же дело? Может формула что-то не то присоветовала?
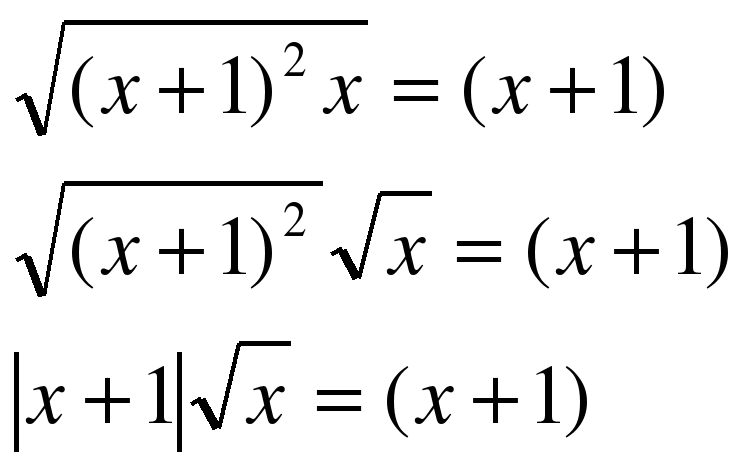 Были корни {-1;1} а стал единственный корень{1}
Были корни {-1;1} а стал единственный корень{1}
Третье путешествие было в страну тригонометрических формул, здесь пришел не с пустыми руками, он смог в закоулках этого княжества отыскать формулу, которая носит имя универсальная тригонометрическая подстановка и с помощью неё он решал уравнение
sin(x)+cos(x)=-1
x=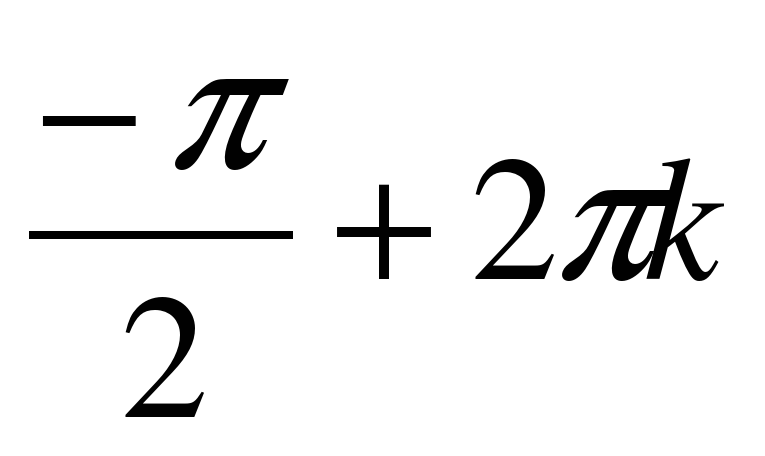
А потом вдруг увидел еще одно решение уравнения, где он его смог потерять? Как вы думаете почему путешествия зашли в тупик ?
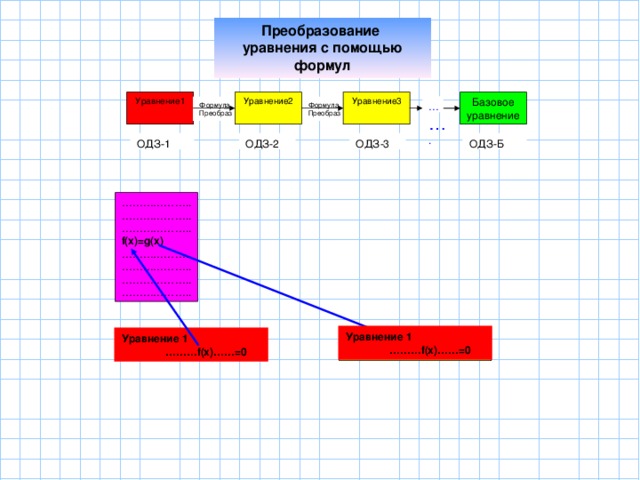
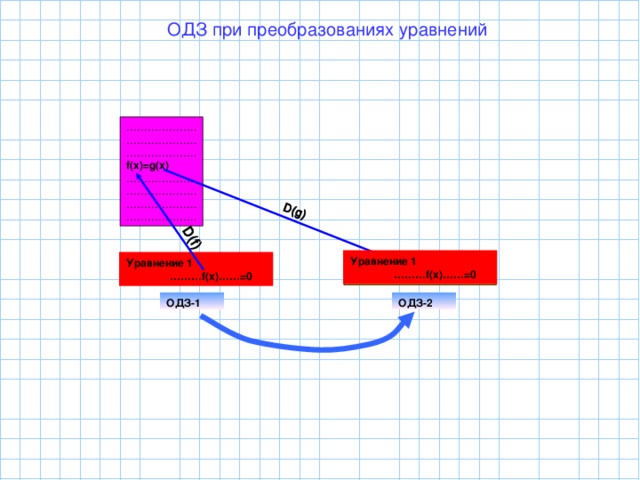
Каждое уравнение имеет свое ОДЗ, давайте вспомним а что же такое ОДЗ уравнения. Ученики формулируют понятие ОДЗ уравнения, как пересечение области определений входящих в него функций. Давайте еще раз посмотрим на схемы преобразований. Демонстрируется слайд
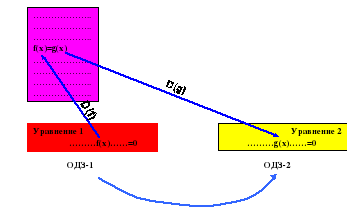
Применение формулы может привести к изменению ОДЗ уравнения, т.е. изменяется область поиска корней уравнения. Какие случаи при этом возможны?
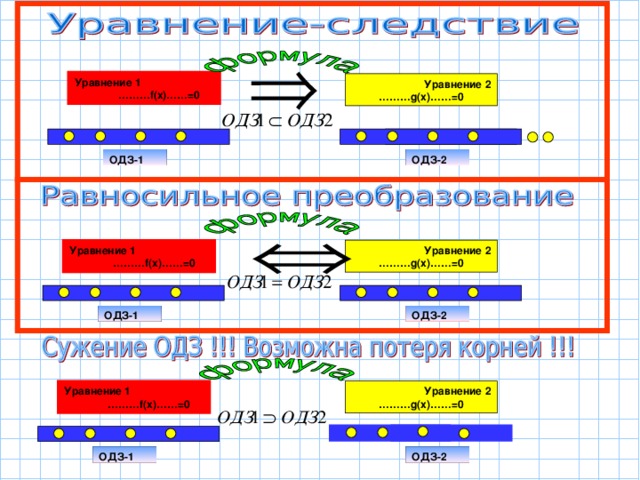
ОДЗ1 ОДЗ2 происходит расширение ОДЗ уравнения, т.е. увеличивается область поиска решений и количество корней может быть больше исходного. Мы переходим к уравнению - следствию, т.е. необходимо произвести проверку корней.
ОДЗ2 происходит расширение ОДЗ уравнения, т.е. увеличивается область поиска решений и количество корней может быть больше исходного. Мы переходим к уравнению - следствию, т.е. необходимо произвести проверку корней.
ОДЗ1=ОДЗ2 применение формулы не изменяет ОДЗ и является равносильным, т.е. корни в уравнении1 и в уравниении2 совпадают.
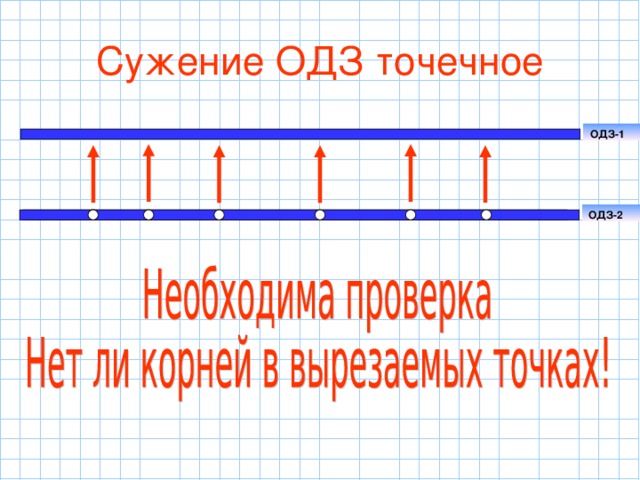
ОДЗ1 ОДЗ2 то происходит сужение ОДЗ уравнения, т.е. уменьшается область поиска решений и количество корней может стать меньше исходного. Сужение может быть на промежуток, тогда неизбежна потеря корней, и сужение на какое-то дискретное множество точек, тогда эти точки можно подставить в уравнение и убедиться нет ли там корней.
ОДЗ2 то происходит сужение ОДЗ уравнения, т.е. уменьшается область поиска решений и количество корней может стать меньше исходного. Сужение может быть на промежуток, тогда неизбежна потеря корней, и сужение на какое-то дискретное множество точек, тогда эти точки можно подставить в уравнение и убедиться нет ли там корней.
Вопрос Какие преобразования были произведены в рассмотренных путешествиях?
Рассмотрим пример применения формул.
Формула вычислительная logc(ab)=logca+logcb
Когда в уравнении мы встречаем формулу логарифм прозведения, то заменяем ее на сумму логарифмов и наоборот, что можно сказать об области определения левой и правой части? Что происходит при переходах от левой части к правой и наоборот? Какой переход приводит к уравнению- следствию? Какой к потере корней?
logca+logcb → logc(ab)
logc(ab) → logca+logcb
Как можно избежать потери корней?
Что изменить в формуле чтобы не возникала потеря корней?
Показывается способы оформления уравнения записи решения логарифмических уравнений: переход к уравнению следствию, равносильный переход и равносильный переход на множестве. На примере уравнения lg x+lg(x+1)=1
Замечание Далеко не всегда нахождения ОДЗ гарантирует нас в получении верного результата, скажем при решении Иррациональных уравнений ограничения накладываются не только на подкоренное выражение, но и на результат.
Пример 
Задание
В тетрадях пометьте формулы преобразования которые могут приводить к изменению ОДЗ значком треугольник с восклицательным знаком.
Составьте из формул помеченных треугольником формулы переходов для уравнений.
Что надо исправить в решении предложенных уравнений, чтобы решение было верным?
Отдельно акцентировать внимание на формуле логарифм степени и разбор случая, когда показатель четный и нечетный.
Итак мы с вами смотрели на путешествия других а теперь давайте сами попробуем свои силы . Предлагаются уравнения
Log3x2=2
lg(3x-17)-lg(x+1)=0
2lg(x-1)=lg(5x+1)
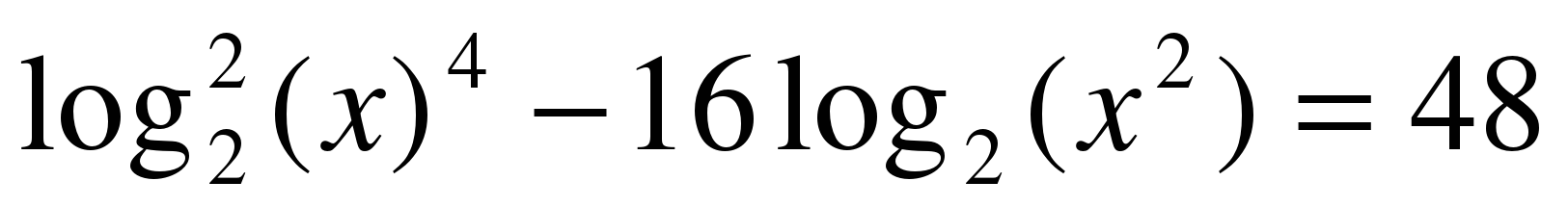
3lg(x2)-lg(-x)=4
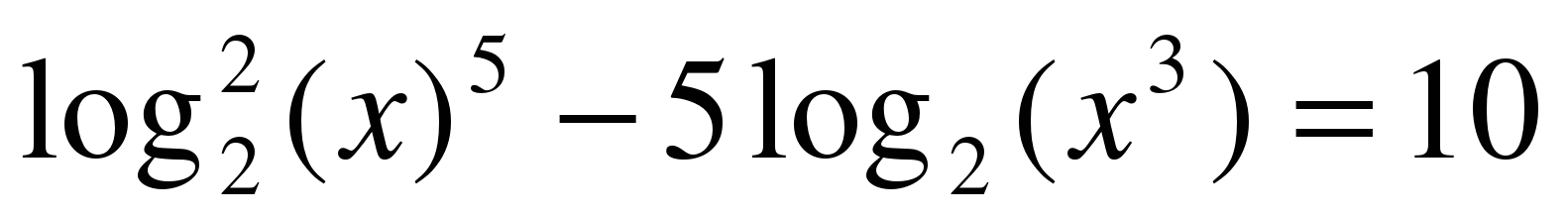
log4(log2x)+log2(log4x)=2
Домашнее задание Доделать предложенные уравнения.
Подводятся итоги урока


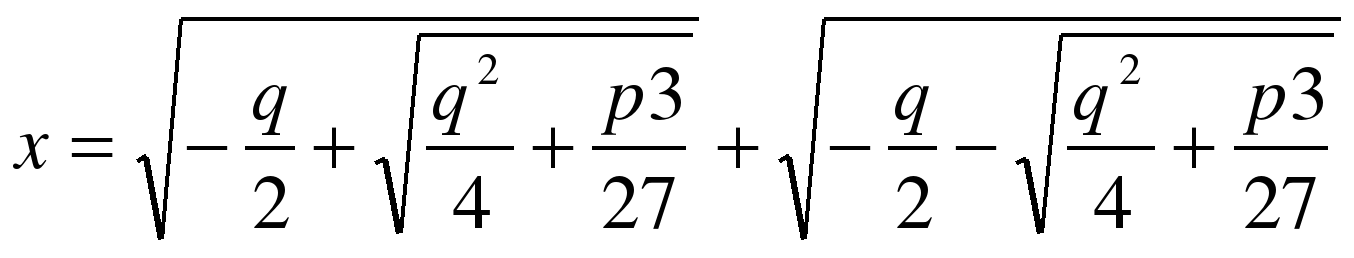 Открыты в 16 веке, Кардано, Тарталье и Ферро. Один корень может быть найден по этой формуле, остальные могут быть отделены с помощью теоремы Безу.
Открыты в 16 веке, Кардано, Тарталье и Ферро. Один корень может быть найден по этой формуле, остальные могут быть отделены с помощью теоремы Безу.


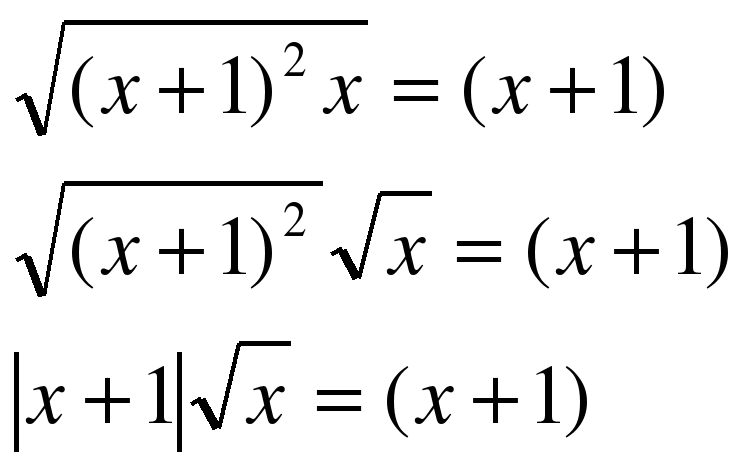 Были корни
Были корни