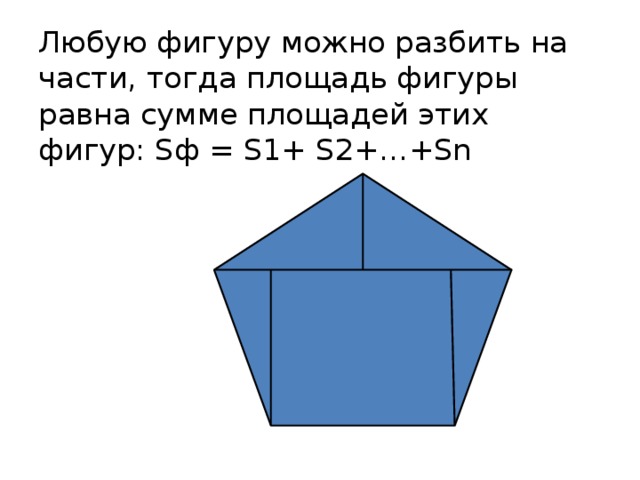
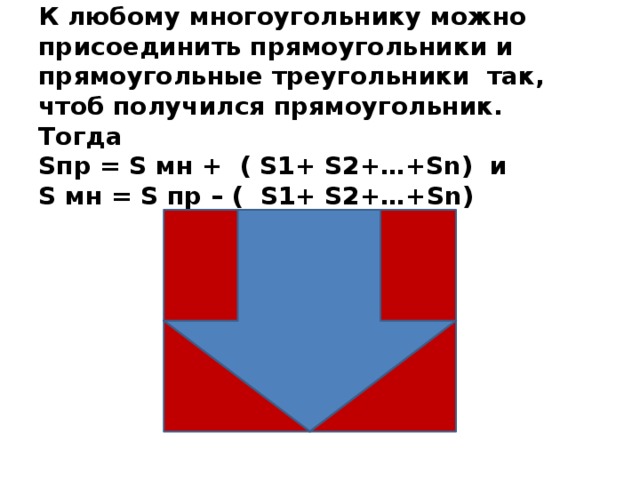
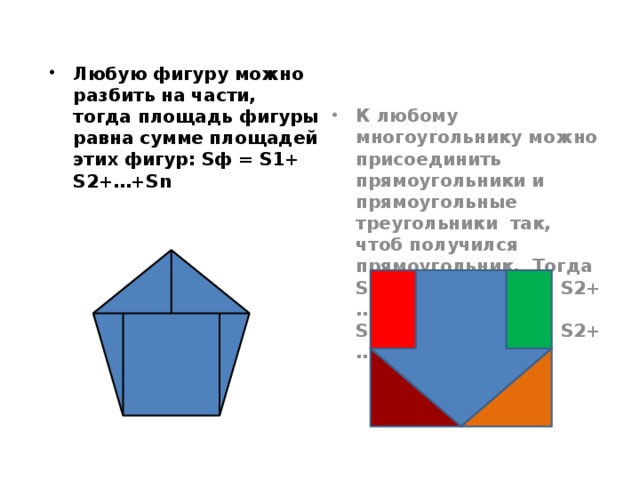
Для каждого выпускника существует своя планка, которую ему надо преодолеть. Некоторым достаточно и 24 баллов, большинство же желает большего.
Но каждый из них должен хорошо решать как минимум 5 – 7 заданий части В. Одно из этих заданий – практико-ориентированная задача В3 « Вычисление площади многоугольника»
Поэтому тему своего мастер – класса я выбрала следующую:
Мастер – класс по теме «Решение задач части В. Площадь многоугольника»
Проблема: найти площадь произвольного многоугольника с вершинами в узлах клетчатой бумаги с клетками размером 1 см Х 1 см. ( на слайде дан произвольный многоугольник на клетчатой бумаге)
Для решения задачи воспользуемся проблемно – поисковым методом.
Мы будем искать всевозможные способы вычисления площади одного и того же многоугольника и среди этих способов выберем один - оптимальный.
Добиваемся следующего:
- Время, затраченное на решение этого задания, было минимальным;
- применение минимума теоретического материала ( необходимо, чтобы этот теоретический материал смог запомнить ученик с любым уровнем знаний);
- результат должен быть точным.
Итак, итог работы: алгоритм вычисления площади представленного многоугольника.
наглядно представить результат своей деятельности в виде информационного листа по теме «Площадь многоугольника».