Тема: « Подготовка к ЕГЭ. Решение текстовых задач».
Тип урока: обобщение и систематизация знаний, умений навыков по теме «Решение текстовых задач».
Форма организации урока: урок- практикум.
Оборудование: интерактивная доска iWboard, мультимедийная презентация, компьютеры по количеству обучающихся.
Цель урока: Подготовка к ЕГЭ. Обобщение и систематизация знаний обучающихся по решению текстовых задач (задание В14) на основе знания основных способов решения алгебраических уравнений из курса алгебры.
Задачи:
1.Обучающая:
- Обобщение и систематизация знаний обучающихся по решению текстовых задач различными способами на основе знания основных способов решения алгебраических уравнений из курса алгебры.
- Создание условий для осознанной подготовки к ЕГЭ.
- Формирование навыков самоконтроля, алгоритмической и компьютерной культуры обучающихся.
2.Развивающая:
- Продолжить развитие устной математической речи, внимания.
- Обеспечение условий для развития умений решать уравнения.
- Совершенствовать мыслительные умения старшеклассников (сравнивать, анализировать, классифицировать, обобщать и навыки обработки информации).
3.Воспитывающая:
- Развитие коммуникативных умений делового общения сверстников.
- Воспитание уверенности в собственных силах.
Особенность урока:
- Целенаправленно и продуктивно подготавливать обучающихся к итоговой аттестации в форме ЕГЭ.
- Поддерживать интерес к познавательному общению, к уроку, к обучению.
Особая роль в сознательном и продуктивном усвоении знаний принадлежит интересу, который может проявляться благодаря использованию ярких примеров, информационно-компьютерных технологий. Учитывая эту особенность, на уроке используется
Тема: « Подготовка к ЕГЭ. Решение текстовых задач».
Тип урока: обобщение и систематизация знаний, умений навыков по теме «Решение текстовых задач».
Форма организации урока: урок- практикум.
Оборудование: интерактивная доска iWboard, мультимедийная презентация, компьютеры по количеству обучающихся.
Цель урока: Подготовка к ЕГЭ. Обобщение и систематизация знаний обучающихся по решению текстовых задач (задание В14) на основе знания основных способов решения алгебраических уравнений из курса алгебры.
Задачи:
1.Обучающая:
- Обобщение и систематизация знаний обучающихся по решению текстовых задач различными способами на основе знания основных способов решения алгебраических уравнений из курса алгебры.
- Создание условий для осознанной подготовки к ЕГЭ.
- Формирование навыков самоконтроля, алгоритмической и компьютерной культуры обучающихся.
2.Развивающая:
- Продолжить развитие устной математической речи, внимания.
- Обеспечение условий для развития умений решать уравнения.
- Совершенствовать мыслительные умения старшеклассников (сравнивать, анализировать, классифицировать, обобщать и навыки обработки информации).
3.Воспитывающая:
- Развитие коммуникативных умений делового общения сверстников.
- Воспитание уверенности в собственных силах.
Особенность урока:
- Целенаправленно и продуктивно подготавливать обучающихся к итоговой аттестации в форме ЕГЭ.
- Поддерживать интерес к познавательному общению, к уроку, к обучению.
Особая роль в сознательном и продуктивном усвоении знаний принадлежит интересу, который может проявляться благодаря использованию ярких примеров, информационно-компьютерных технологий. Учитывая эту особенность, на уроке используется
Тема: « Подготовка к ЕГЭ. Решение текстовых задач».
Тип урока: обобщение и систематизация знаний, умений навыков по теме «Решение текстовых задач».
Форма организации урока: урок- практикум.
Оборудование: интерактивная доска iWboard, мультимедийная презентация, компьютеры по количеству обучающихся.
Цель урока: Подготовка к ЕГЭ. Обобщение и систематизация знаний обучающихся по решению текстовых задач (задание В14) на основе знания основных способов решения алгебраических уравнений из курса алгебры.
Задачи:
1.Обучающая:
- Обобщение и систематизация знаний обучающихся по решению текстовых задач различными способами на основе знания основных способов решения алгебраических уравнений из курса алгебры.
- Создание условий для осознанной подготовки к ЕГЭ.
- Формирование навыков самоконтроля, алгоритмической и компьютерной культуры обучающихся.
2.Развивающая:
- Продолжить развитие устной математической речи, внимания.
- Обеспечение условий для развития умений решать уравнения.
- Совершенствовать мыслительные умения старшеклассников (сравнивать, анализировать, классифицировать, обобщать и навыки обработки информации).
3.Воспитывающая:
- Развитие коммуникативных умений делового общения сверстников.
- Воспитание уверенности в собственных силах.
Особенность урока:
- Целенаправленно и продуктивно подготавливать обучающихся к итоговой аттестации в форме ЕГЭ.
- Поддерживать интерес к познавательному общению, к уроку, к обучению.
Особая роль в сознательном и продуктивном усвоении знаний принадлежит интересу, который может проявляться благодаря использованию ярких примеров, информационно-компьютерных технологий. Учитывая эту особенность, на уроке используетсяТема: « Подготовка к ЕГЭ. Решение текстовых задач».
Тип урока: обобщение и систематизация знаний, умений навыков по теме «Решение текстовых задач».
Форма организации урока: урок- практикум.
Оборудование: интерактивная доска iWboard, мультимедийная презентация, компьютеры по количеству обучающихся.
Цель урока: Подготовка к ЕГЭ. Обобщение и систематизация знаний обучающихся по решению текстовых задач (задание В14) на основе знания основных способов решения алгебраических уравнений из курса алгебры.
Задачи:
1.Обучающая:
- Обобщение и систематизация знаний обучающихся по решению текстовых задач различными способами на основе знания основных способов решения алгебраических уравнений из курса алгебры.
- Создание условий для осознанной подготовки к ЕГЭ.
- Формирование навыков самоконтроля, алгоритмической и компьютерной культуры обучающихся.
2.Развивающая:
- Продолжить развитие устной математической речи, внимания.
- Обеспечение условий для развития умений решать уравнения.
- Совершенствовать мыслительные умения старшеклассников (сравнивать, анализировать, классифицировать, обобщать и навыки обработки информации).
3.Воспитывающая:
- Развитие коммуникативных умений делового общения сверстников.
- Воспитание уверенности в собственных силах.
Особенность урока:
- Целенаправленно и продуктивно подготавливать обучающихся к итоговой аттестации в форме ЕГЭ.
- Поддерживать интерес к познавательному общению, к уроку, к обучению.
Особая роль в сознательном и продуктивном усвоении знаний принадлежит интересу, который может проявляться благодаря использованию ярких примеров, информационно-компьютерных технологий. Учитывая эту особенность, на уроке используетсяТема: « Подготовка к ЕГЭ. Решение текстовых задач».
Тип урока: обобщение и систематизация знаний, умений навыков по теме «Решение текстовых задач».
Форма организации урока: урок- практикум.
Оборудование: интерактивная доска iWboard, мультимедийная презентация, компьютеры по количеству обучающихся.
Цель урока: Подготовка к ЕГЭ. Обобщение и систематизация знаний обучающихся по решению текстовых задач (задание В14) на основе знания основных способов решения алгебраических уравнений из курса алгебры.
Задачи:
1.Обучающая:
- Обобщение и систематизация знаний обучающихся по решению текстовых задач различными способами на основе знания основных способов решения алгебраических уравнений из курса алгебры.
- Создание условий для осознанной подготовки к ЕГЭ.
- Формирование навыков самоконтроля, алгоритмической и компьютерной культуры обучающихся.
2.Развивающая:
- Продолжить развитие устной математической речи, внимания.
- Обеспечение условий для развития умений решать уравнения.
- Совершенствовать мыслительные умения старшеклассников (сравнивать, анализировать, классифицировать, обобщать и навыки обработки информации).
3.Воспитывающая:
- Развитие коммуникативных умений делового общения сверстников.
- Воспитание уверенности в собственных силах.
Особенность урока:
- Целенаправленно и продуктивно подготавливать обучающихся к итоговой аттестации в форме ЕГЭ.
- Поддерживать интерес к познавательному общению, к уроку, к обучению.
Особая роль в сознательном и продуктивном усвоении знаний принадлежит интересу, который может проявляться благодаря использованию ярких примеров, информационно-компьютерных технологий. Учитывая эту особенность, на уроке используетсяТема: « Подготовка к ЕГЭ. Решение текстовых задач».
Тип урока: обобщение и систематизация знаний, умений навыков по теме «Решение текстовых задач».
Форма организации урока: урок- практикум.
Оборудование: интерактивная доска iWboard, мультимедийная презентация, компьютеры по количеству обучающихся.
Цель урока: Подготовка к ЕГЭ. Обобщение и систематизация знаний обучающихся по решению текстовых задач (задание В14) на основе знания основных способов решения алгебраических уравнений из курса алгебры.
Задачи:
1.Обучающая:
- Обобщение и систематизация знаний обучающихся по решению текстовых задач различными способами на основе знания основных способов решения алгебраических уравнений из курса алгебры.
- Создание условий для осознанной подготовки к ЕГЭ.
- Формирование навыков самоконтроля, алгоритмической и компьютерной культуры обучающихся.
2.Развивающая:
- Продолжить развитие устной математической речи, внимания.
- Обеспечение условий для развития умений решать уравнения.
- Совершенствовать мыслительные умения старшеклассников (сравнивать, анализировать, классифицировать, обобщать и навыки обработки информации).
3.Воспитывающая:
- Развитие коммуникативных умений делового общения сверстников.
- Воспитание уверенности в собственных силах.
Особенность урока:
- Целенаправленно и продуктивно подготавливать обучающихся к итоговой аттестации в форме ЕГЭ.
- Поддерживать интерес к познавательному общению, к уроку, к обучению.
Особая роль в сознательном и продуктивном усвоении знаний принадлежит интересу, который может проявляться благодаря использованию ярких примеров, информационно-компьютерных технологий. Учитывая эту особенность, на уроке используется
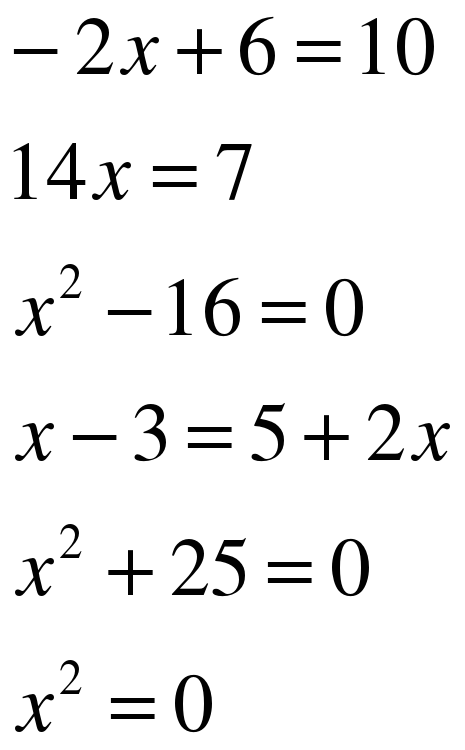

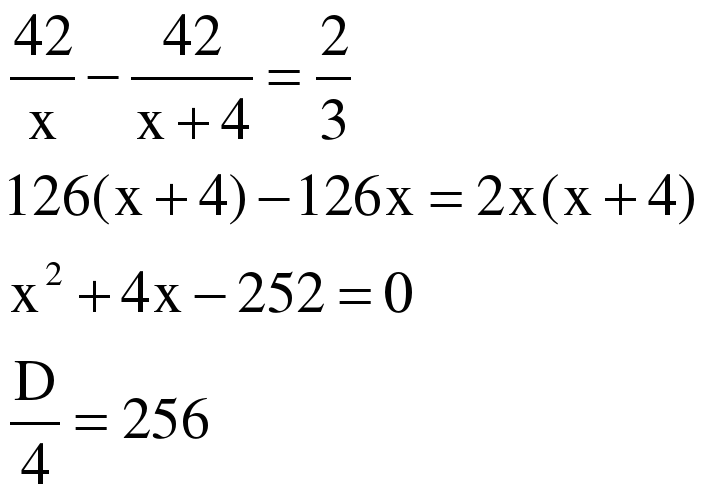
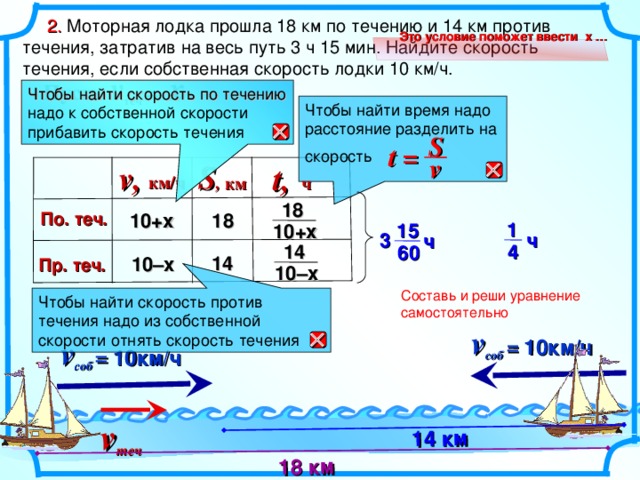
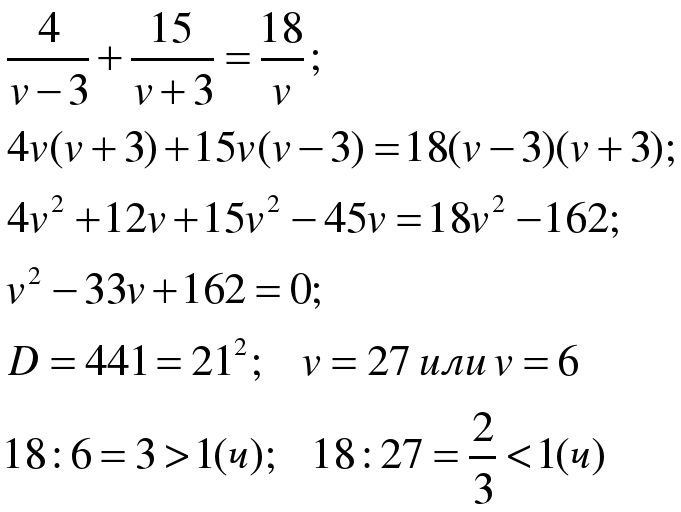 атер прошел 4 км против течения реки и 15 км – по течению за то же время, которое ему понадобилось для прохождения 18 км по озеру. Найдите собственную скорость катера, если известно, что скорость течения реки равна 3 км/ч и 18 км по озеру катер проходит за время меньшее 1 часа.
атер прошел 4 км против течения реки и 15 км – по течению за то же время, которое ему понадобилось для прохождения 18 км по озеру. Найдите собственную скорость катера, если известно, что скорость течения реки равна 3 км/ч и 18 км по озеру катер проходит за время меньшее 1 часа. 
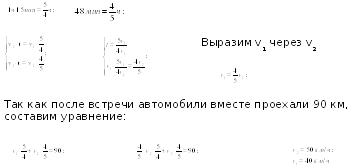












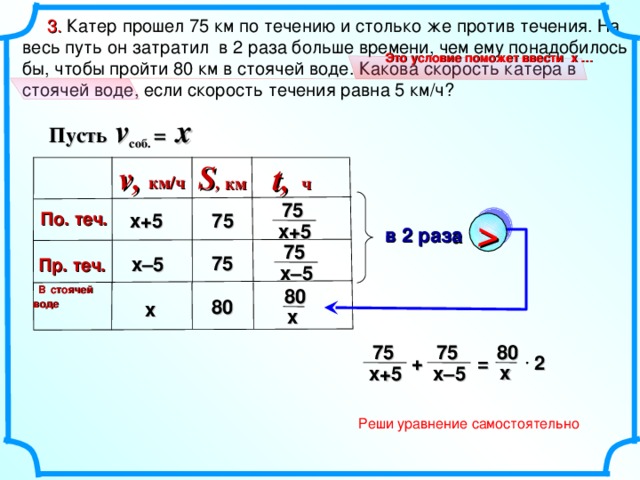 3. Катер прошел 75 км по течению и столько же против течения. На весь путь он затратил в 2 раза больше времени, чем ему понадобилось бы, чтобы пройти 80 км в стоячей воде. Какова скорость катера в стоячей воде, если скорость течения равна 5 км/ч? Это условие поможет ввести х … Пусть v соб. = x S , v, t, км/ч ч км 75 По. теч. х+5 75 х+5 75 75 х – 5 Пр. теч. В стоячей воде х–5 80 80 х х Глава III , 9 класс. 9.2 Физика . Задача 9. 2 .34 Бродский И.Л., Видус А.М., Коротаев А.Б. Сборник текстовых задач по математике ля профильных классов. 7-11 классы/ Под ред. И.Л. Бродского. М.: АРКТИ, 2004. – 140с. 80 75 75 2 + = х х–5 х+5 Реши уравнение самостоятельно 12" width="640"
3. Катер прошел 75 км по течению и столько же против течения. На весь путь он затратил в 2 раза больше времени, чем ему понадобилось бы, чтобы пройти 80 км в стоячей воде. Какова скорость катера в стоячей воде, если скорость течения равна 5 км/ч? Это условие поможет ввести х … Пусть v соб. = x S , v, t, км/ч ч км 75 По. теч. х+5 75 х+5 75 75 х – 5 Пр. теч. В стоячей воде х–5 80 80 х х Глава III , 9 класс. 9.2 Физика . Задача 9. 2 .34 Бродский И.Л., Видус А.М., Коротаев А.Б. Сборник текстовых задач по математике ля профильных классов. 7-11 классы/ Под ред. И.Л. Бродского. М.: АРКТИ, 2004. – 140с. 80 75 75 2 + = х х–5 х+5 Реши уравнение самостоятельно 12" width="640"
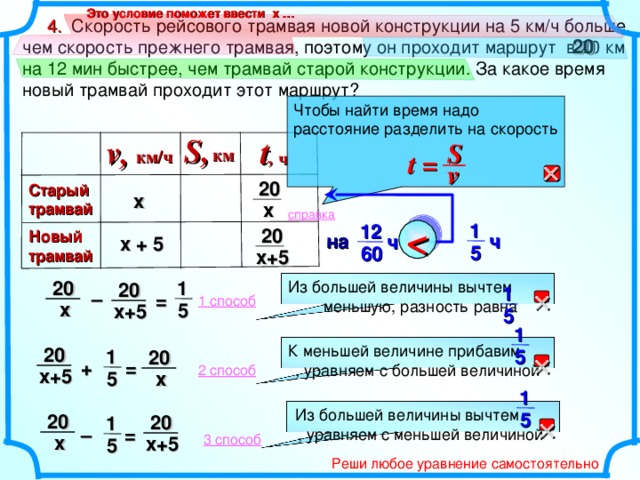






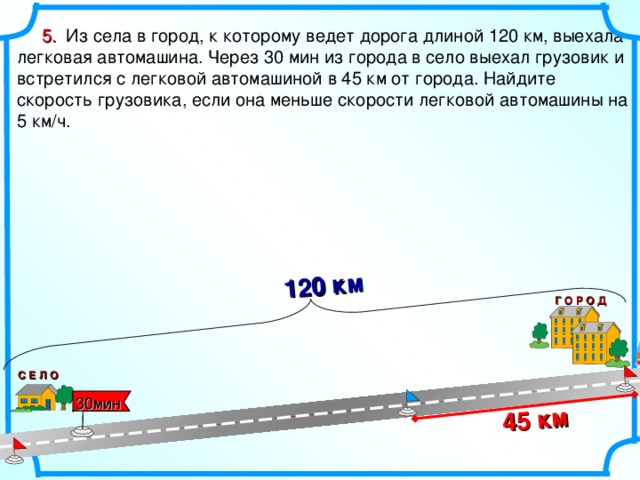
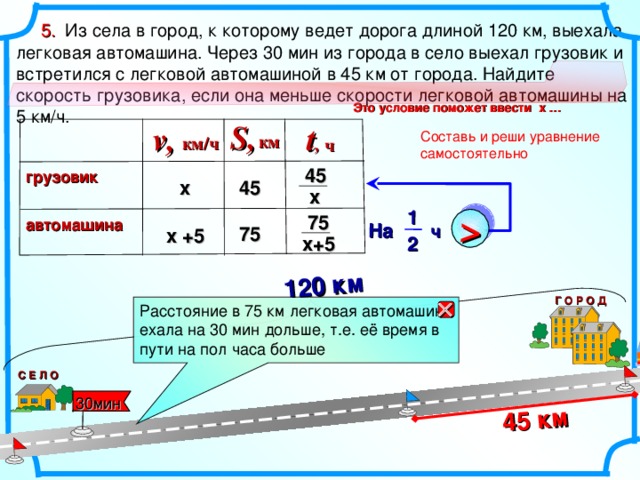 1 2 5. Из села в город, к которому ведет дорога длиной 120 км, выехала легковая автомашина. Через 30 мин из города в село выехал грузовик и встретился с легковой автомашиной в 45 км от города. Найдите скорость грузовика, если она меньше скорости легковой автомашины на 5 км/ч. Это условие поможет ввести х … S, v, t , Составь и реши уравнение самостоятельно км км/ч ч 45 грузовик х 45 х 75 автомашина 75 х +5 х+5 Г О Р О Д Расстояние в 75 км легковая автомашина ехала на 30 мин дольше, т.е. её время в пути на пол часа больше Глава III, 9 класс. 9.2 Физика Задача 9.2.38 Бродский И.Л., Видус А.М., Коротаев А.Б. Сборник текстовых задач по математике ля профильных классов. 7-11 классы/ Под ред. И.Л. Бродского. М.: АРКТИ, 2004. – 140с. С Е Л О 30мин 21" width="640"
1 2 5. Из села в город, к которому ведет дорога длиной 120 км, выехала легковая автомашина. Через 30 мин из города в село выехал грузовик и встретился с легковой автомашиной в 45 км от города. Найдите скорость грузовика, если она меньше скорости легковой автомашины на 5 км/ч. Это условие поможет ввести х … S, v, t , Составь и реши уравнение самостоятельно км км/ч ч 45 грузовик х 45 х 75 автомашина 75 х +5 х+5 Г О Р О Д Расстояние в 75 км легковая автомашина ехала на 30 мин дольше, т.е. её время в пути на пол часа больше Глава III, 9 класс. 9.2 Физика Задача 9.2.38 Бродский И.Л., Видус А.М., Коротаев А.Б. Сборник текстовых задач по математике ля профильных классов. 7-11 классы/ Под ред. И.Л. Бродского. М.: АРКТИ, 2004. – 140с. С Е Л О 30мин 21" width="640"





 0) Ответ: скорость первого велосипедиста 14 км/ч. Задачи Условие" width="640"
0) Ответ: скорость первого велосипедиста 14 км/ч. Задачи Условие" width="640"

























