Площадь параллелограмма

Урок геометрии в 8 классе по теме "Площадь параллелограмма" с использованием электронно-образовательных ресурсов

Цели урока:

1. Обучающие:

- Вывести формулу для вычисления площади параллелограмма,

- Совершенствовать навыки решения задач.

2. Развивающие:

- Содействовать развитию у обучающихся самостоятельности и способности к самоорганизации,

- Содействовать развитию навыка исследовательской и познавательной деятельности у обучающихся,

- Содействовать развитию умения анализтировать, сравнивать и обобщать.

3. Воспитательные:

- Содействовать формированию толерантности и умения работать в группах.

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«Конспект»

ТЕМА: ПЛОЩАДЬ ПАРАЛЛЕЛОГРАММА. УРОК 1

ЦЕЛИ УРОКА

Обучающие:

Вывести формулу для вычисления площади параллелограмма;
Совершенствовать навыки решения задач.

Развивающие:

Содействовать развитию у обучающихся самостоятельности и способности к самоорганизации;
Содействовать развитию навыка исследовательской и познавательной деятельности у обучающихся;
Содействовать развитию умения анализировать, сравнивать и обобщать.

Воспитательные:

Содействовать формированию толерантности и умения работать в группах.

ТИП УРОКА: Изучение нового материала.

ОБОРУДОВАНИЕ:

Мультимедийный проектор;
Карточки для исследовательской деятельности;
Карточки для самостоятельной работы.

ХОД УРОКА

I. Организационный момент

-Здравствуйте, ребята!

Сегодня мы продолжим изучение площадей многоугольников

Слайд 1

II. Актуализация опорных знаний

Чтобы узнать площадь какого многоугольника мы будем сегодня находить, вы должны расшифровать тему, записанную на экране. Каждое число закрывает свою букву. Чтобы узнать, какая буква скрывается за числом, вы должны ответить на вопросы. В слове может быть несколько одинаковых букв.

Чему равна площадь квадрата со стороной 2 см? (4)
Найти периметр квадрата со стороной 0,5 см (2)
На сколько букв больше в слове «гипотенуза», чем в слове «катет»? (5)
Найти площадь прямоугольника со сторонами 2 см и 3 см. (6)
Найти сторону квадрата, если его площадь 9 см². (3)

У нас остались неоткрытыми звездочки. Чтобы их убрать, нужно будет выполнить следующее задание.

На экране вы видите утверждение, которое мы изучали в 7 классе. Чисто математическая формулировка должна быть достаточно полной, но без ненужных слов. Найдите ненужные слова в следующих знакомых вам предложениях:

- Сумма двух острых углов прямоугольного треугольника равна 90˚.

- Если катет прямоугольного треугольника равен половине гипотенузы, то противолежащий ему острый угол содержит 30˚.

Итак, тема нашего урока «Площадь параллелограмма».

Запишите в тетради число и тему урока.

Слайд 2

Слайд 3

III. Усвоение новых знаний и способов действий

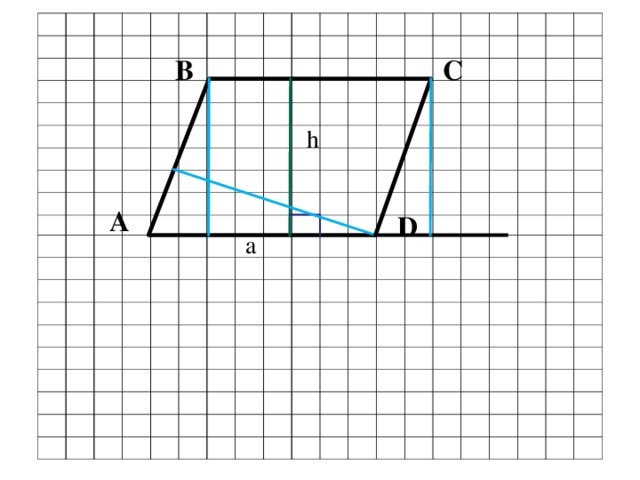
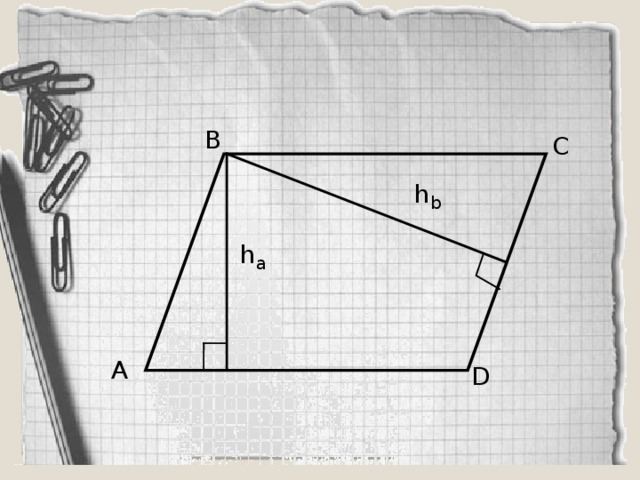
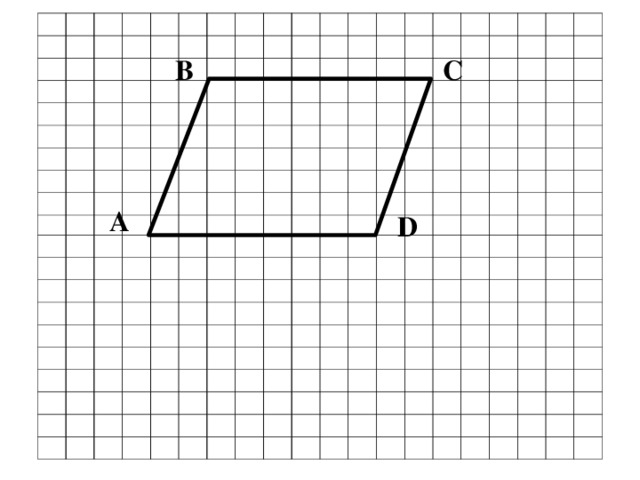
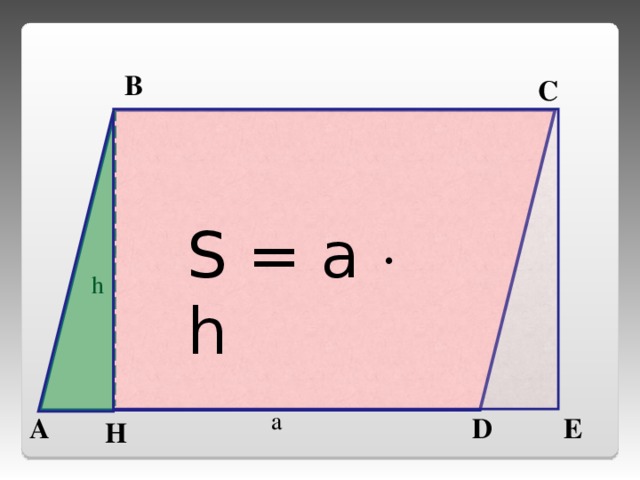
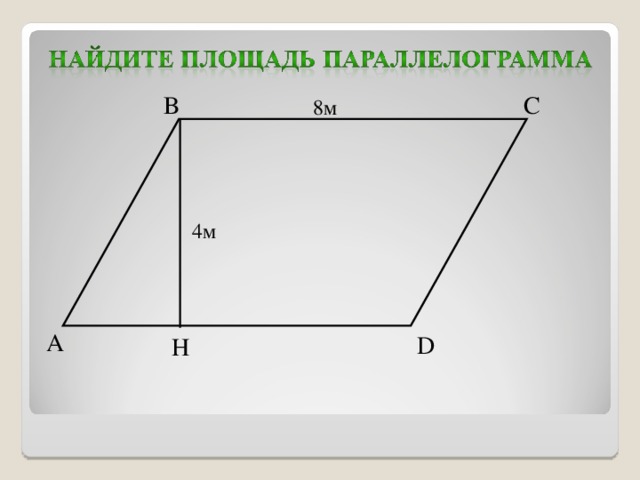
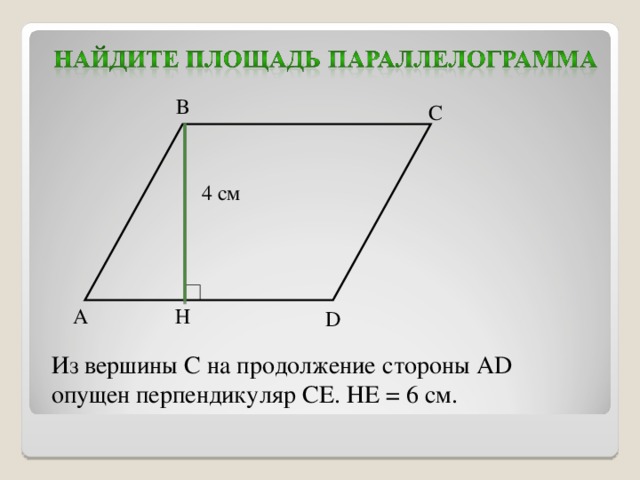
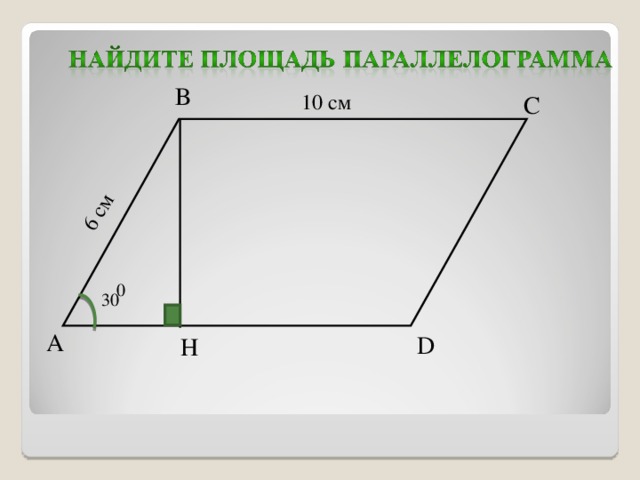
Какая же фигура называется параллелограммом?

Найдите среди данных многоугольников параллелограммы.

Почему вы решили, что эти фигуры являются параллелограммом?

Постройте параллелограмм АВСД. На доске сетка - клеточки, как в тетради. Одну сторону параллелограмма назовем основанием. Подпишем. Проведем перпендикуляр из любой точки противоположной стороны к прямой, содержащей основание. Такой перпендикуляр называется высотой параллелограмма.

Сколько таких перпендикуляров можно провести? Много

Что можно сказать об их длине? Равны

Из какой точки нам удобнее провести перпендикуляр? Из вершины

Построим высоту из точки С. Чтобы построить перпендикуляр к основанию АД, продолжим прямую АД.

Если мы примем другую сторону за основание, то соответственно будет и другая высота.

Показать на чертеже.

Итак, высота – перпендикуляр из любой точки противоположной стороны к прямой, содержащей основание.

Обозначим высоту и основание для удобства маленькими латинскими буквами.

На экране вы видите параллелограмм. Назовите основание и высоту в каждом параллелограмме.

Вспомним тему урока. Мы должны вывести формулу для вычисления площади параллелограмма. Подсчитаем площадь нашего параллелограмма в клеточках.

Считают.

Удобно ли вам было находить площадь?

Это неудобно, т.к. клеточки нецелые.

Давайте попробуем упростить свою работу.

Формулы площади каких фигур мы уже знаем?

Как найти площадь квадрата?

Как найти площадь прямоугольника?

Давайте воспользуемся одной из них. Для этого надо решить, какую из этих фигур напоминает параллелограмм. (Прямоугольник)

У вас на столах фигуры. /Приложение 1/Составьте параллелограмм. Как из параллелограмма получить прямоугольник? Вы можете переставить часть параллелограмма и составить из полученных частичек прямоугольник.

Молодцы. А площадь прямоугольника мы можем вычислить?

Как мы вычислили площадь прямоугольника?

Чему она равна?

Что тогда можно сказать о площади параллелограмма?

Почему мы можем сделать такой вывод?

Показать на чертеже на экране.

Каким свойством мы воспользовались?

Из каких многоугольников состоит прямоугольник?

Из каких многоугольников состоит параллелограмм?

А почему из данных частичек получился параллелограмм? (треугольники равны)

Почему эти треугольники равны? (по гипотенузе и острому углу)

Итак, можем сделать вывод, что площадь параллелограмма тоже можем вычислить по формуле площади прямоугольника.

Сравните вычисленную площадь по формуле и сосчитанную по клеточкам.

Докажем теорему.

Площадь параллелограмма равна произведению его основания на высоту.

Слайд 4

Слайд 5

Слайд 6

Слайд 7

IV. Первичная проверка понимания

Решаем устно

Пусть а – основание, h – высота, а S – площадь параллелограмма.

А) найти S, если а = 14 см, h= 5 cм.

Б) найти а, если S=32 cм², h=16 cм.

На столах лежат параллелограммы, /Приложение 2/площади которых нам нужно найти. Возьмите первый параллелограмм. Что нужно знать для нахождения площади параллелограмма? Измерьте высоту и основание и найдите его площадь. Запишите данные и вычисления в тетрадь.

Возьмите второй параллелограмм. Постройте высоту, выполните необходимые измерения и найдите площадь параллелограмма. Запишите данные и вычисления в тетрадь.

Слайды 9-12

V. Обобщение и систематизация знаний

Решение задач из учебника №№ 459(а-в), 464(а)

VI. Подведение итогов урока

Итак, что мы с вами узнали на уроке?

Что такое высота?

Как называется сторона параллелограмма, к которой проведена высота?

Как найти площадь параллелограмма?

Запишем домашнее задание: п. 51, № 459(г), 464 (б).

Откройте п. 51. Отметим, что вы должны выучить. Что называется основанием и высотой. Теорему о площади параллелограмма.

Откройте задачи.

Нужно найти значение выражения, как мы делали на уроке.