Урок геометрии в 8-м классе по теме "Площадь параллелограмма"
Цели урока:
- Повторить свойства площадей фигур; формулы площади прямоугольника и квадрата; вывести формулу для нахождения площади параллелограмма; рассмотреть задачи с её применением.
- Развивать умения анализировать, сопоставлять, логически мыслить, обобщать; развивать внимание, память, активность и самостоятельность.
- Воспитывать ответственное отношение к учебному труду, настойчивость для достижения конечного результата, умение работать в коллективе; воспитывать в учащихся личностную рефлексию: стал ли он сам для себя изменяющимся субъектом деятельности.
Ход урока.
1. Организационный момент.
2. Мотивация урока.
Ребята, урок я начну с высказывания Г.Галилея: «Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать». Я хочу, чтобы вы на уроке думали и рассуждали.
3. Актуализация опорных знаний. Проверка д/з.
6 cм
По рисунку составить задачу и решить.
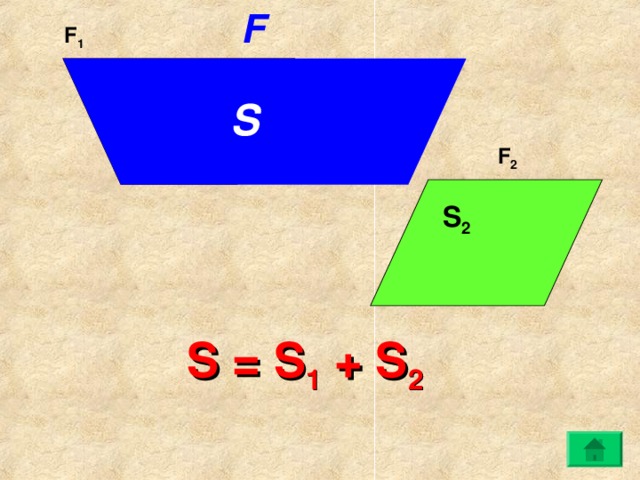
S2
?
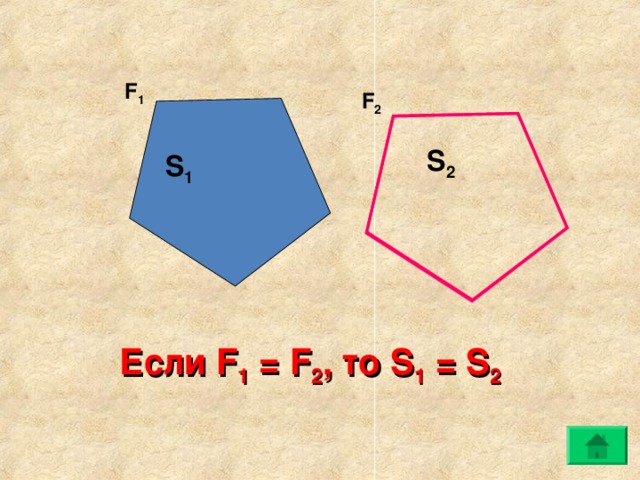
S1=S2.
4 см
S1
1)
2) А D
SABCD = Q
SΔ ABC =?
В С
Найдите площадь дачного участка такой формы.
Определение и свойства параллелограмма
- А какие Вы знаете свойства? (сторон, углов, диагоналей).
- Дети, Вы всё знаете о данной фигуре? (нет, площадь).
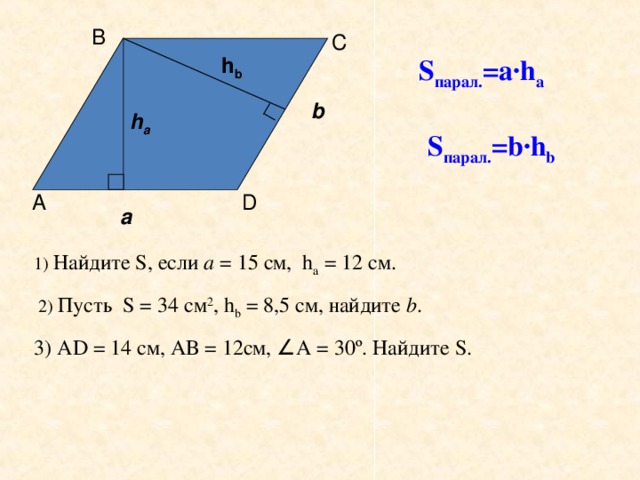
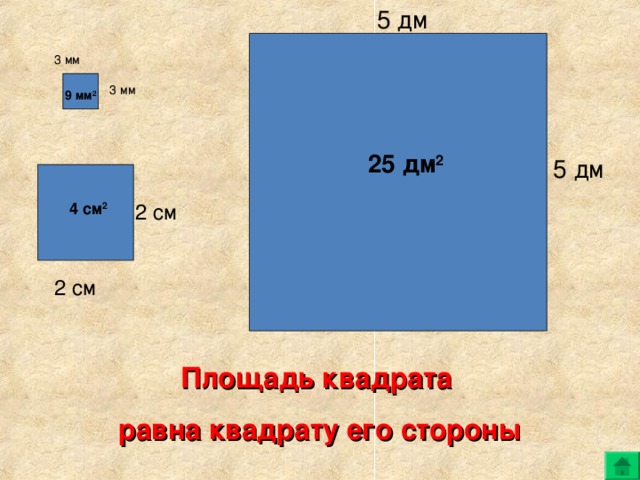
- Площадь каких фигур Вы знаете? (Sкв=а2; Sпрям=а*b).
- А Вы знаете, чему равна площадь параллелограмма? (нет).
- О чём мы сегодня будем говорить на уроке геометрии? (Sпарал).
Итак, вы сегодня на уроке будет учениками «Евклида» и исследуете параллелограмм и докажите чему равна площадь параллелограмма.
4. Объяснение нового материала
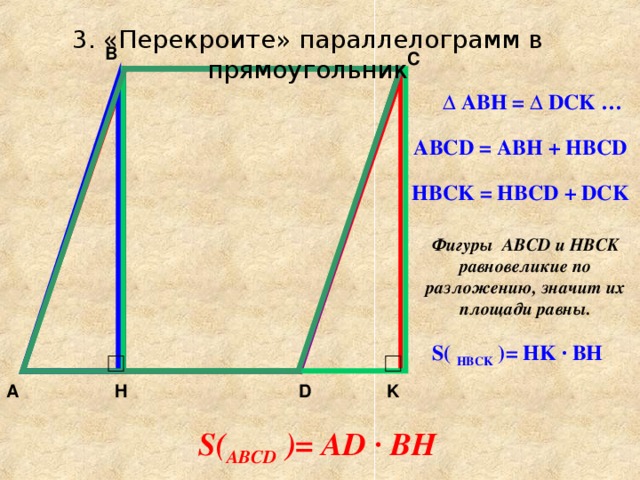
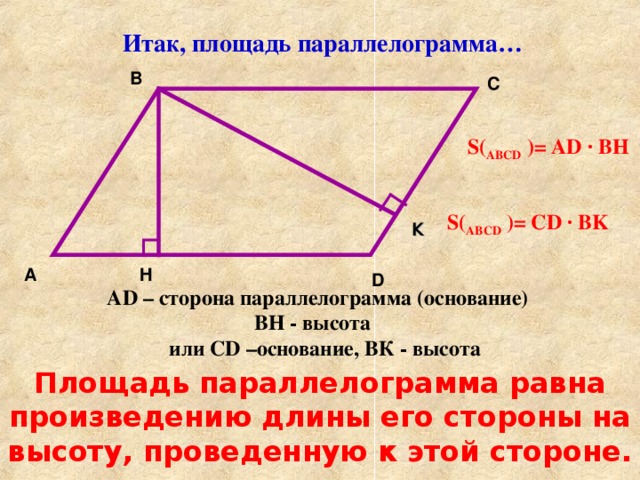
Вывод формулы площади параллелограмма.
Задача.
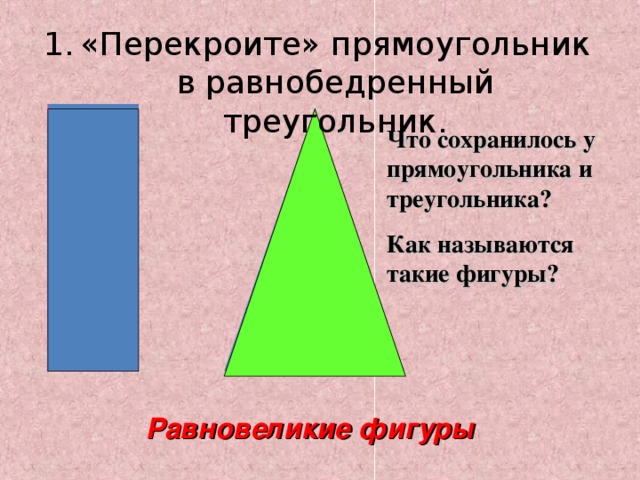
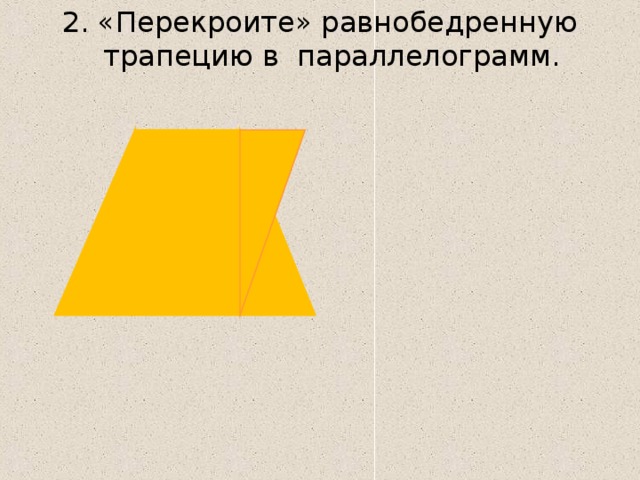
Как «перекроить» параллелограмм, чтобы получить прямоугольник с такой же площадью?
После вывода формулы учитель требует ее словесное описание. Несколько учеников «проговариваются» вслух, тем самым, развивая математическую речь.
Найти площадь фигуры.
Теорема о площади ромба по его диагоналям.
Площадь ромба равна половине произведения его диагоналей.
Рассмотреть доказательство теоремы на с. 142.
5. Минутки релаксации:
- Быстро поморгать, закрыть глаза и посидеть спокойно, медленно считая до пяти. Повторить 4-5 раз.
- Вытянуть правую руку вперёд. Следить глазами, не поворачивая головы, за медленным движением указательного пальца вытянутой руки влево и вправо, вверх и вниз. Повторить 4-5 раз.
- В среднем темпе проделать 3-4 круговых движения глазами в правую сторону, столько же в левую сторону. Расслабив глазные мышцы, посмотреть вдаль на счет 1-6. Повторить 1-2 раза.
6. Первичное закрепление нового материала.
Решить:
устно № 721, 722, 723, 724;
письменно № 725 (1, 2), 726(1, 2), 727(1, 2), 732, 743(1).
7. Самостоятельная работа учащихся.
Решить № 725(3), 726(3).
8. Итог урока.
9. Рефлексия. Д/з.
Выучить п.17, решить № 727(3, 4), 743(2), 729(1).