Площадь параллелограмма.
«Считай несчастным тот день или тот час,
в который ты не усвоил ничего нового
и ничего не прибавил к образованию».
Ян Амос Каменский
Цель урока: изучить теорему о площади параллелограмма.
Задачи урока:
· образовательные – формирование практических навыков вычисления площадей многоугольников в ходе решения задач (квадрат, прямоугольник, параллелограмм);
· развивающие – активизация мыслительной деятельности: перенос знаний в новую ситуацию;
· воспитательные – развитие познавательного интереса, культуры математической речи, способности критически, объективно оценивать действия товарищей и свои.
Оборудование: компьютер, проектор, бумажные модели параллелограмма, презентация.
Ход урока.
Организационный момент.
- Какую тему мы начали изучать два урока назад?
- Сегодня на уроке мы научимся вычислять площадь еще одной фигуры – параллелограмма.
- В тетрадях число, классная работа, тема урока.
Актуализация знаний учащихся.
- Площади каких фигур вычислять мы умеем?
- Как найти площадь квадрата?
- Как вычислить площадь прямоугольника?
- Проверим некоторые задачи из домашней работы.
Приготовить рисунки на доске. Выходит уч-ся и устно объясняет решение.
№ 454.
№ 456.
Изучение нового материала.
- Начертите в тетради квадрат, прямоугольник и параллелограмм.
- Подпишите под ними формулы для нахождения площади этих фигур.
- Что нужно знать для нахождения площади квадрата? Что такое а в квадрате? Какие эти стороны? (перпендикулярные)
- Что нужно знать для нахождения площади прямоугольника?
- Какие это стороны?
- Как вы думаете, как мы будем искать площадь параллелограмма?
- Эти стороны перпендикулярны?
- А как получить перпендикулярный отрезок, который можно использовать для нахождения площади параллелограмма?
- Это отрезок называется высотой параллелограмма.
- С помощью чего удобно проводить перпендикуляр?
- Сколько высот можно провести из одной вершины?
- Итак, вынесем предположение о том, как мы будем находить площадь параллелограмма.
И сейчас мы докажем, что вы оказались правы.
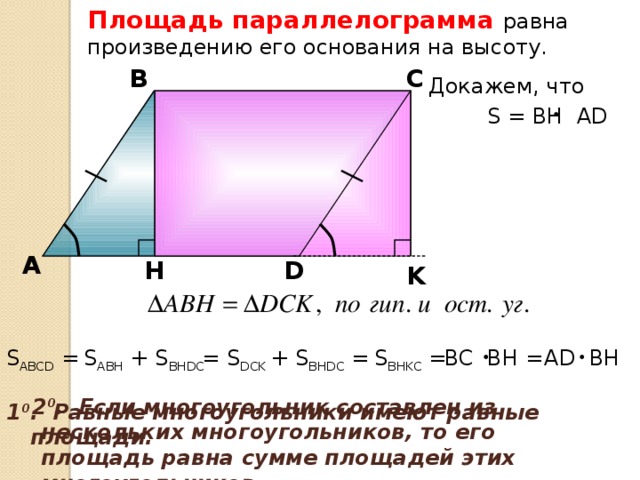
- Доказательство теоремы по слайду презентации.
- Найдем подтверждение нашей правоты в учебнике. По оглавлению находим главу 6 параграф 2 пункт «Площадь параллелограмма». Прочитаем теорему.
Закрепление изученного.
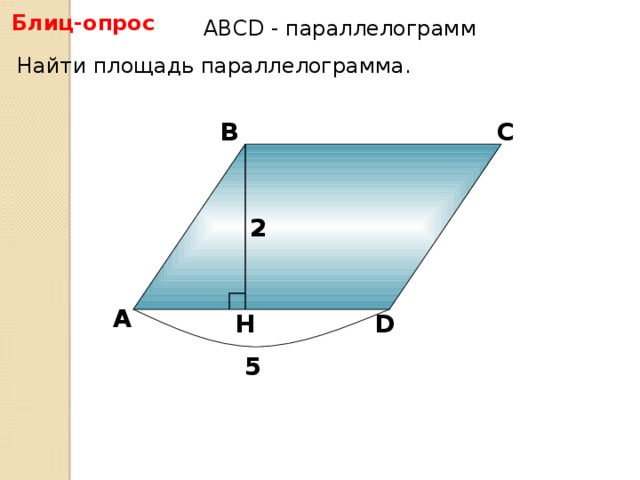
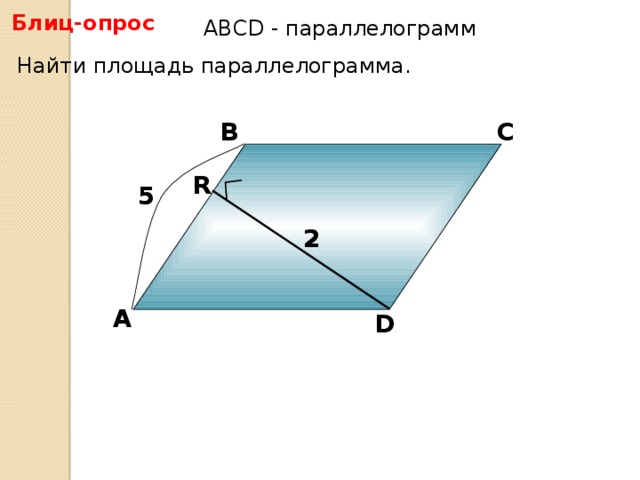
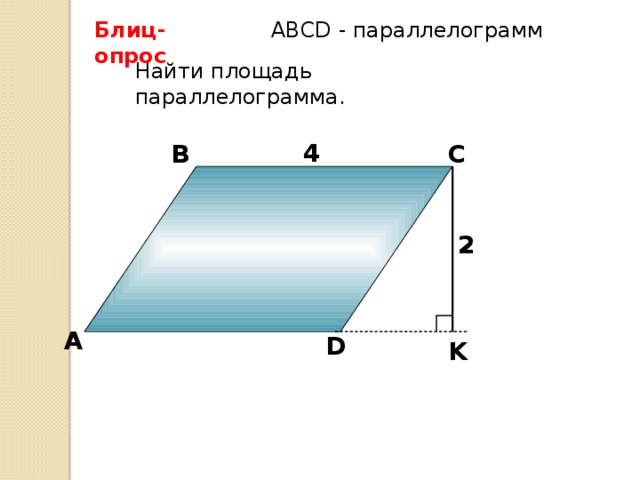
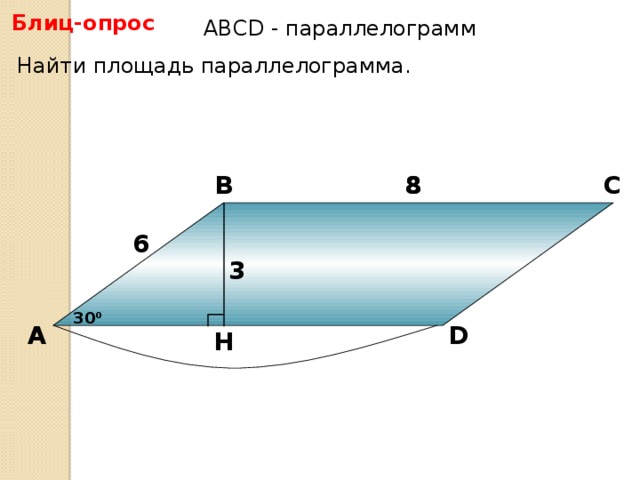
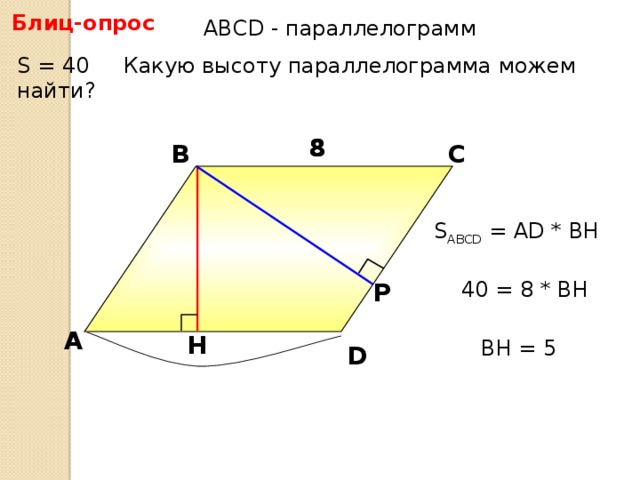
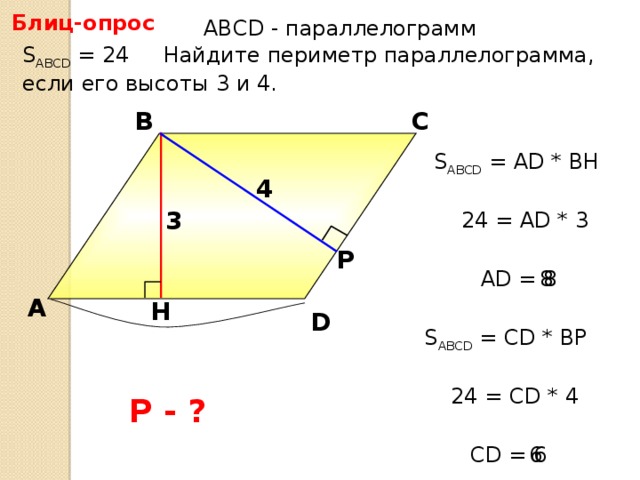
- Задачи со слайдов. Решение первых трех задач устное, следующих трех - письменное.
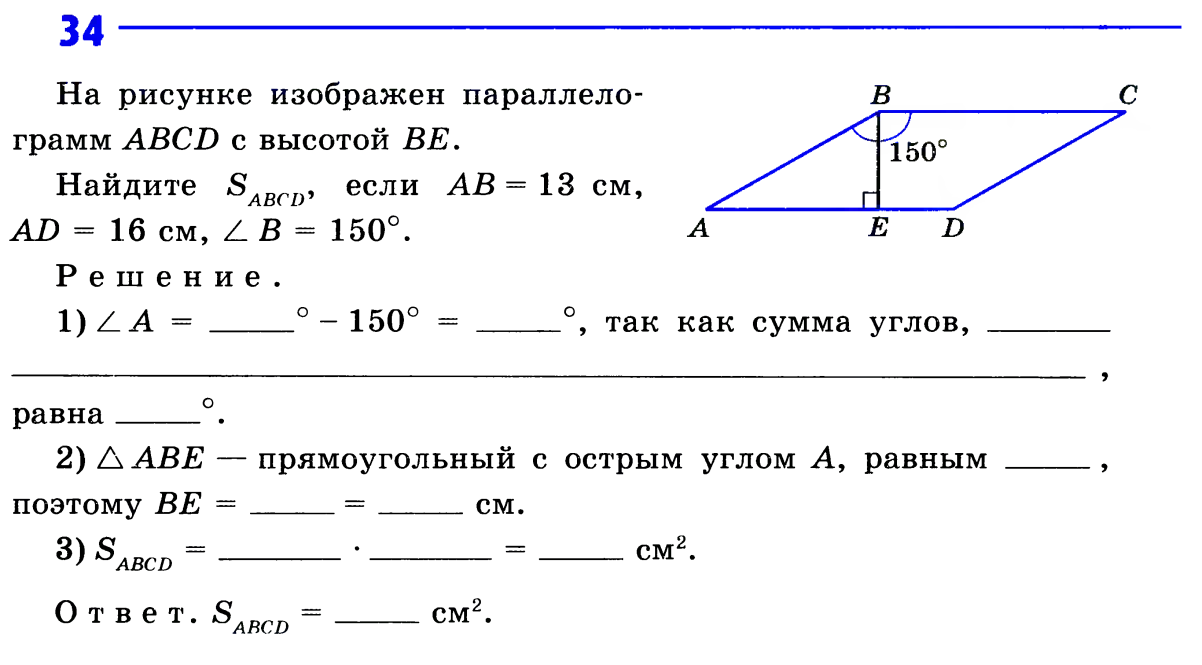
- Работа в рабочих тетрадях № 33, 34.
- № 463 из учебника.
Подведение итогов урока.
- Вернемся к словам Яна Амоса Каменского. Как вы оцените этот урок: как счастливый час или несчастный?
- Сумели ли вы усвоить новое?
- Что удалось вам прибавить к образованию?
Домашнее задание.
П. 51 – теорема + доказательство; №№ 459ав, 460, 464а.
Литература.
- Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. Геометрия, 7-9.
- Л.С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков, И.И. Юдина. Рабочая тетрадь по геометрии для 8 класса.
 а)
а)