Воронежской области.
Урок - исследование по геометрии в 8 классе.
| Этапы урока | Время | Содержание деятельности учителя | Содержание деятельности ученика | Использование ИКТ |
| Организацион-ный момент. |
| Здравствуйте, рада приветствовать всех собравшихся в этом классе. У нас урок геометрии. Я пожелаю вам и себе учебной плодотворной работы. Эпиграфом к нашему занятию я взяла слова великого итальянского физика Галилео Галилея: «Геометрия является самым могущественным средством для изощрения умственных способностей и дает нам возможность правильно мыслить и рассуждать». | Класс разбит на 4 группы. | 
|
| Актуализация опорных знаний. |
| -Давайте вспомним какую тему мы изучали на последних уроках? -Запишите тему урока. У каждой группы на столах ЛИСТОК КОНТРОЛЯ. После выполнения каждого задания, вы будете заносить в листок контроля полученные баллы. А в конце урока мы подведем итоги. Итак, устная работа. А в это время по 1 человеку с каждой группы работают с тестом» (приложение1) РАЗДЕЛ «Определения». 20. Дайте определение параллелограмма. 40.Какой многоугольник называется выпуклым? 60.Какие треугольники называются пифагоровыми? РАЗДЕЛ «Теоремы». 20. Теорема Пифагора. 40.Теорема, обратная теореме Пифагора 60.Теорема об отношении площадей двух треугольников, имеющих по равному углу. РАЗДЕЛ «Свойства». 20. Особое свойство прямоугольника. 40.Основные свойства площадей многоугольников. 60.Основные свойства квадрата. | -Площади фигур. Теорема Пифагора. |

Презентация. |
|
|
|
РАЗДЕЛ «Площадь четырехугольника». |
|
|
|
|
| 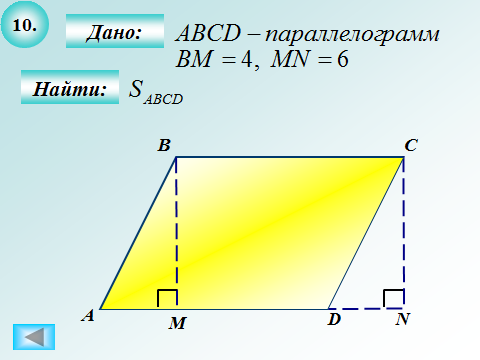 Ответ: 24 Ответ: 24
| 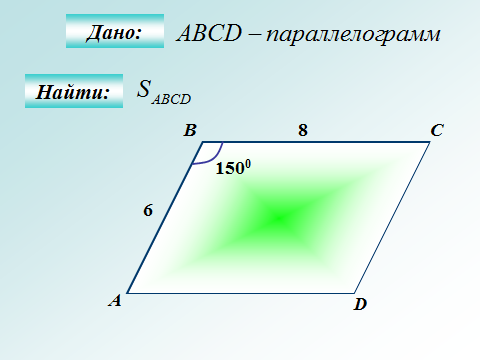 Ответ: 24 Ответ: 24
| 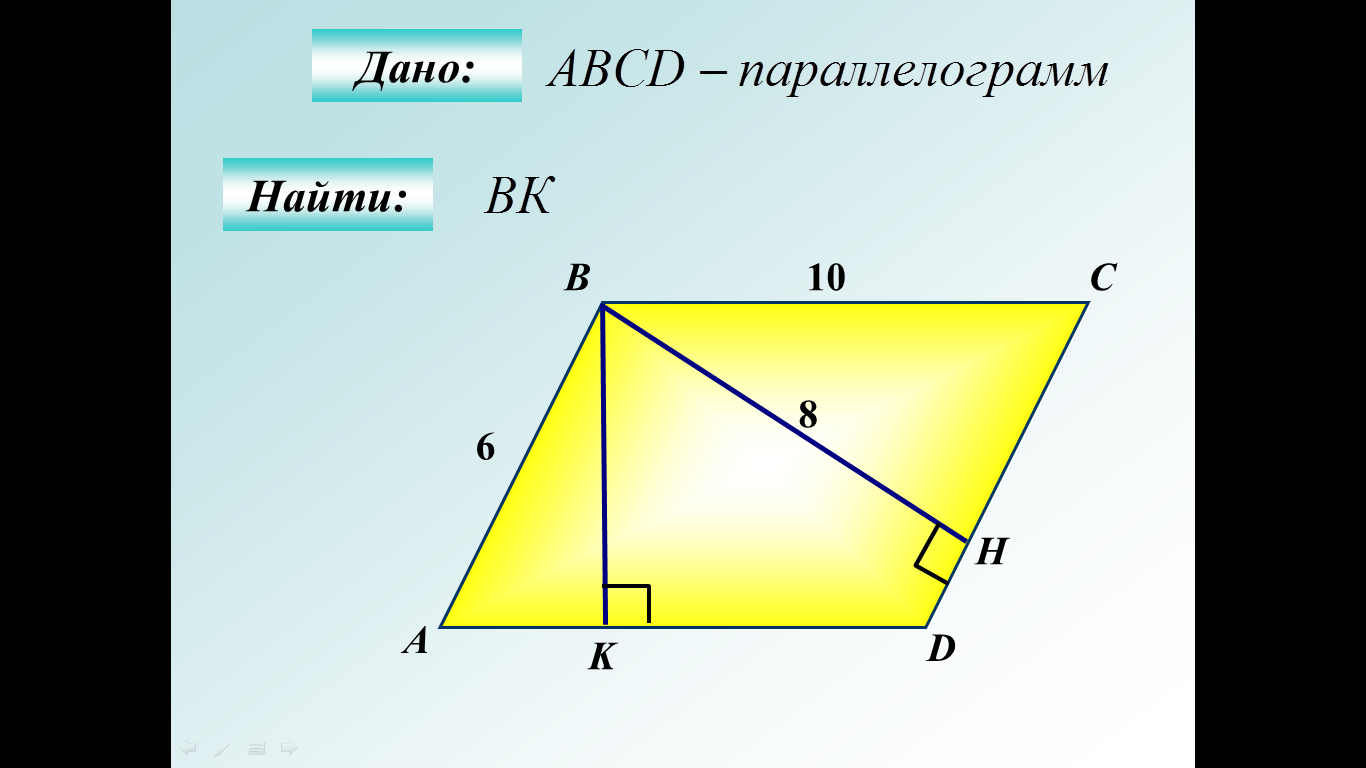 Ответ:4,8 Ответ:4,8
|
|
|
|
РАЗДЕЛ «Площадь треугольника». |
|
|
|
|
| 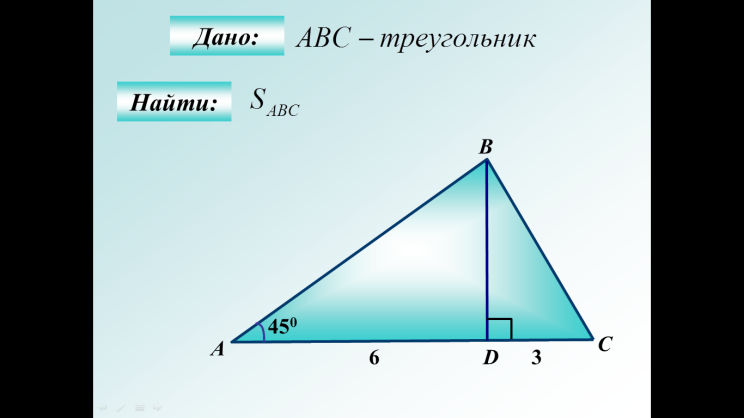
Ответ:27 | 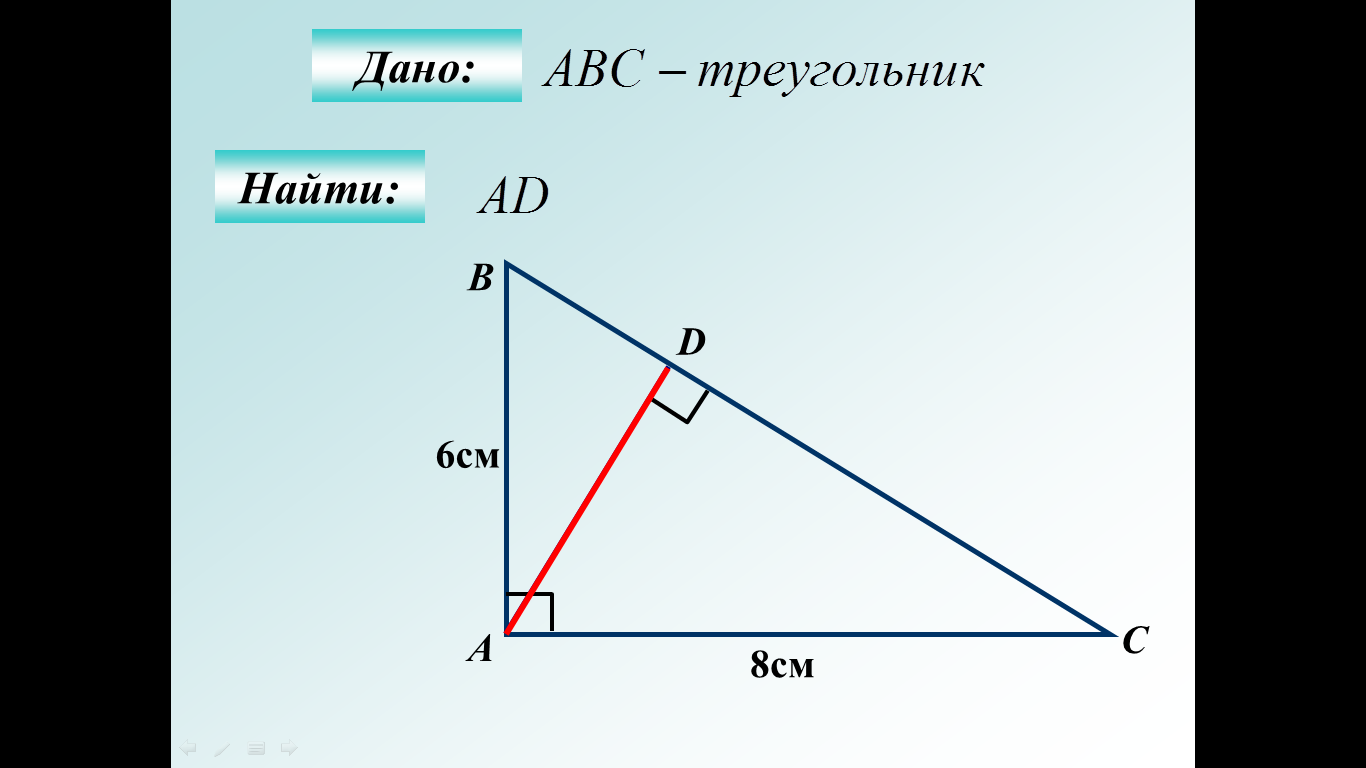 Ответ:27 Ответ:27
| Ответ:42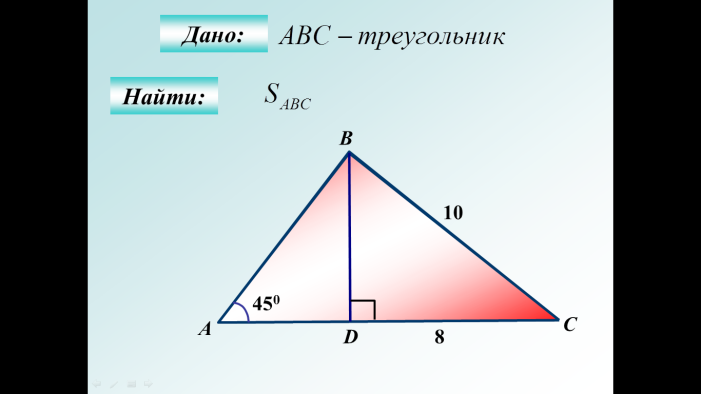 |
|
|
| РАЗДЕЛ «Теорема Пифагора». |
|
|
|
|
| 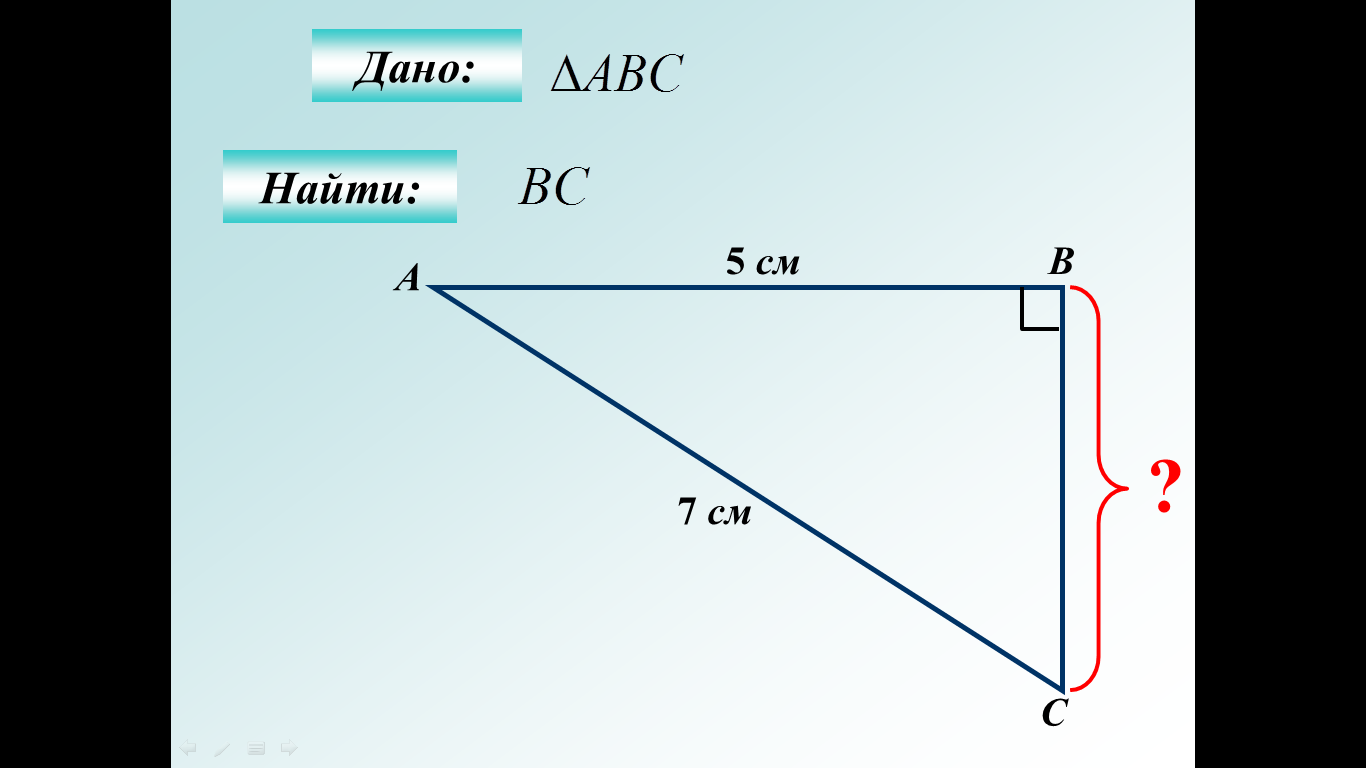 Ответ: Ответ:
| 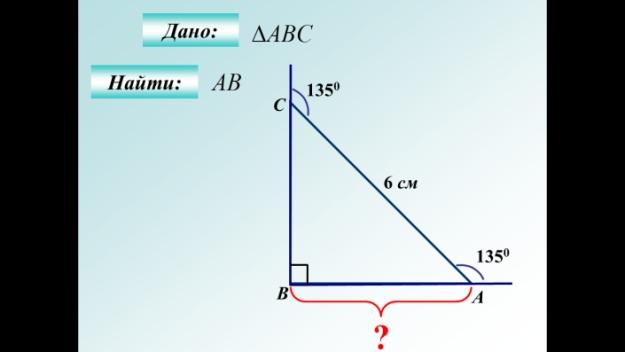
Ответ: | 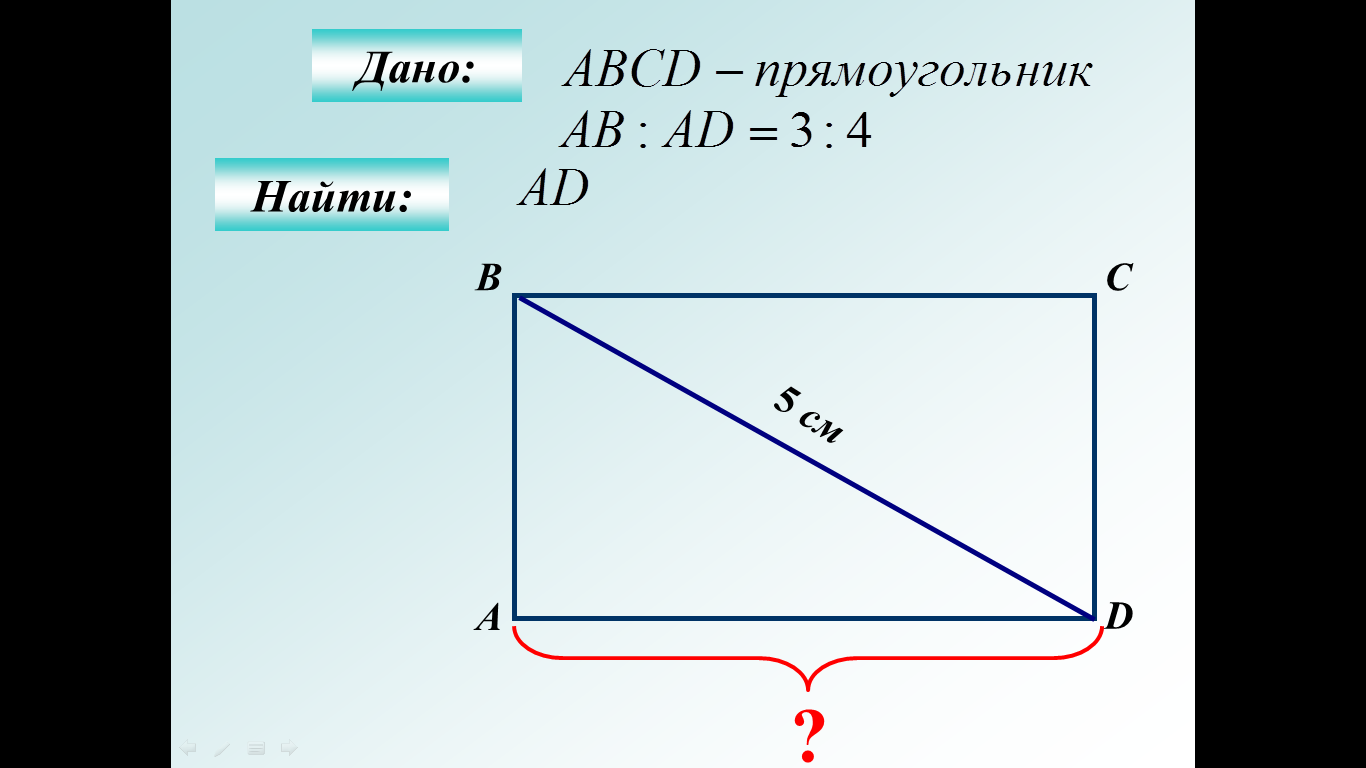 Ответ: 4 Ответ: 4
|
| Исследовательс-кая работа |
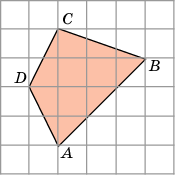
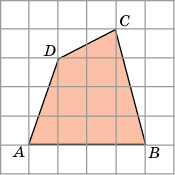
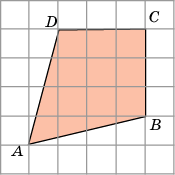
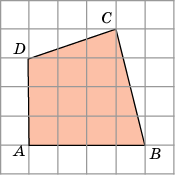
| А вы знаете, ребята, что традиционно при сдаче ЕГЭ в 11 классе наибольшую трудность у выпускников вызывают геометрические задачи. Поэтому сегодня я для вас подготовила задания, встречающиеся на ЕГЭ. ЗАДАНИЕ: У вас на столах лежат листы с заданиями из открытого банка заданий ЕГЭ по математике. Вы должны вычислить площади заданных многоугольников. Каждой команде дается лист с заданиями.(Приложение 2) |
|
|
| Физминутка. |
| Рисуй глазами треугольник. Теперь его переверни Вершиной вниз. И вновь глазами Ты по периметру веди. Рисуй восьмерку вертикально. Ты головою не крути, А лишь глазами осторожно Ты вдоль по линиям води. И на бочок ее клади. Теперь следи горизонтально, И в центре ты остановись. Зажмурься крепко, не ленись. Глаза открываем мы, наконец, Зарядка окончилась. Ты- молодец! |
|
|
| Изучение нового материала. |
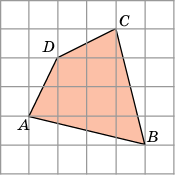
| -Давайте подведем итог наших исследований. (Каждая группа показывает свое решение) -Итак, дана клетчатая бумага, ширина одной клетки равна 1см. На ней изображена фигура, в данном случае треугольник. И нам требуется найти площадь этого треугольника.
|
| 
|
|
|
| "Считаем по клеткам" 1.Посчитаем количество полных клеток внутри данного треугольника. 2.Дополним неполные клетки друг другом до полных клеток 3.Сложим полученные количества полных клеток:
|
| 
|
|
|
| "Формула площади фигуры" -Давайте вспомним формулу для нахождения площади треугольника. -По рисунку определим, чему равны основание и высота треугольника. -А теперь нам только осталось подставить эти значения в готовую формулу. |
| 
|
|
|
| "Сложение площадей фигур" -Разобьем данный треугольник на два прямоугольных треугольника, для этого проведем высоту. -Найдем площадь прямоугольного треугольника S1. -Найдем площадь прямоугольного треугольника S2. -Площадь искомого треугольника найдем по формуле: S =S1+S2 -Идея этого способа состоит в том, что мы должны разбить данную фигуру на более простые фигуры, чтобы затем найти их площади и сложить их. |
| 
|
|
|
| "Вычитание площадей фигур" -А мы переходим к следующему способу решения задачи. Он в некотором случае противоположен методу разбиения, это наоборот: достраивание до прямоугольника. -Достроим до прямоугольника со сторонами 5 на 6. -Найдем площадь прямоугольника S . -Найдем площадь прямоугольного треугольника S1. -Найдем площадь прямоугольного треугольника S2. -Площадь искомого треугольника найдем по формуле: Sтр=Sпр – (S1+S2)
|
| 
|
|
|
| Формула Пика - Это еще один метод для нахождения площадей фигур, который не входит в школьную программу, но он ОЧЕНЬ прост и КРАСИВ. Георг Алекса́ндр Пик –австрийский математик, который жил в 20 веке. В чем состоит формула Пика? -Если дан многоугольник на некоторой клетчатой решетке, вершины которого находятся в узлах этой клетчатой решетки, то его площадь можно найти по следующей формуле:S=Г/2+В-1 |
| 
|
|
|
| - А теперь проверьте, правильно ли вы нашли площади своих многоугольников, используя еще один из методов. |
|
|
| Закрепление нового материала. |
| Задачи для самостоятельного .решения. |
Ответ:10 | 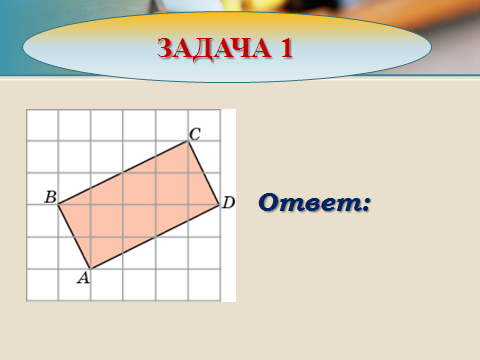
|
|
|
|
|
Ответ:6 | 
|
|
|
|
|
Ответ:9 | 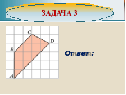
|
| Итог урока. |
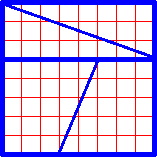
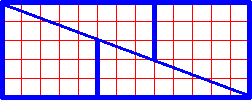
| Дан квадрат 8 на 8 см. Не трудно посчитать площадь этого квадрата. Она равна 64 м2. Этот квадрат разрезали и сложили прямоугольник. Но прямоугольник получился 13 на 5 см, т.е. площадь его равна 65 см2. -Почему так получилось? Ответ: Если вы действительно проделаете все указанные действия, то сразу заметите, что половинки не сходятся по диагональной линии. На самом деле, вместо общей диагонали есть две ломаные линии, и внутри прямоугольника образуется пустое пространство. Площадь этого пустого пространства как раз и равна площади одного маленького квадратика, который якобы возник из ничего. |
| 
Гиперссылка на пример |
| Рефлексия. |
| Выберите из данных утверждений то, которое на сегодняшнем уроке стало ближе всего.
|
|
|


 Ответ: 24
Ответ: 24 Ответ: 24
Ответ: 24 Ответ:4,8
Ответ:4,8
 Ответ:27
Ответ:27
 Ответ:
Ответ: 
 Ответ: 4
Ответ: 4