| № | Этап урока | Название используемых ЭОР (с указанием порядкового номера из Таблицы 2) | Деятельность учителя (с указанием действий с ЭОР, например, демонстрация) | Деятельность ученика | Время (в мин.)
|
| 1 | 2 | 3 | 4 | 5 | 6 |
Мотивационно-ориентировочная часть | 5 мин |
| 1.1 | Самоопределение к учебной деятельности | Видео с притчей http://my.mail.ru/list/drt19801983/video/423/687.html?time=64&from=videoplayer | Перед началом урока хочу предложить вам старинную суфийскую притчу «Делёж верблюдов». - Живший некогда Суфий хотел сделать так, чтобы ученики после его смерти нашли подходящего им учителя Пути. Поэтому в завещании, после обязательного по закону раздела имущества, он оставил своим ученикам семнадцать верблюдов с таким указанием: «Разделите верблюдов между самым старшим, средним по возрасту и самым младшим из вас следующим образом: старшему пусть будет половина, среднему — треть, а младшему — одна девятая». Когда Суфий умер, и завещание было прочитано, ученики вначале были изумлены таким неумелым распределением имущества Мастера. Одни предлагали: «Давайте владеть верблюдами сообща»; другие искали совета и затем говорили: «Нам советовали разделить способом, наиболее близким к указанному»; третьим судья посоветовал продать верблюдов и поделить деньги; а ещё некоторые считали, что завещание утратило свою законную силу, поскольку его условия не могут быть выполнены. Спустя некоторое время ученики пришли к мысли, что в завещании Мастера мог быть какой-то скрытый смысл, и они стали расспрашивать повсюду о человеке, который может решать неразрешимые задачи. К кому бы они ни обращались, никто не мог помочь им, пока они не постучали в дверь Хазрата Али, зятя Пророка. Он сказал: «Вот вам решение. Я добавлю одного верблюда к этим семнадцати. Из восемнадцати верблюдов вы возьмете половину — девять верблюдов — для старшего ученика. Второй ученик возьмет треть — то есть шесть верблюдов. Третий получит одну девятую — двух верблюдов. Это как раз семнадцать. Остался один — мой верблюд, он вернётся ко мне». Вот так ученики нашли себе учителя.
- Какой серьёзной темой мы начали заниматься в этой четверти? - Чему мы уже научились?
- Как вы думаете, куда дальше в изучении дробей мы продолжим продвигаться?
|
- обыкновенные дроби
-сокращать дроби, отмечать их на координатном луче, приводить к наименьшему общему знаменателю, сравнивать дроби с разными знаменателями, складывать дроби с одинаковыми знаменателями, выделять целую часть. - мы должны научиться производить с ними все арифметические действия.
|
|
| 1.2 | Актуализация знаний |
| - А начнём мы как всегда с устной работы, потому что, чтобы узнать что-то новое ... Задания для устной работы: (презентация) 1) Составь неправильную дробь и перейди к смешанному числу. 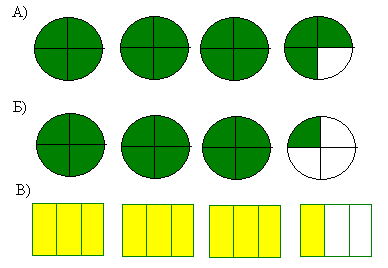
2) Определи координату обозначенных точек на координатном луче. Что называют координатным лучом?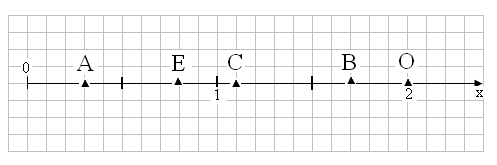
3) Сократите дроби: , , , . 4) Выделите целую часть из дробей: , , , . 5) Дан ряд дробей: , , , . Что мы можем о нём сказать? К какому наименьшему общему знаменателю можно привести все дроби? Почему? Приведите все дроби к знаменателю 24. Прочитайте получившейся ряд чисел. 6) Найдите сумму дробей. Если потребуется, сократите дроби и выделите целую часть: а) + ; б) + . -А каким правилом сложения дробей вы воспользовались? Давайте восстановим алгоритм сложения дробей с одинаковыми знаменателями.
предыдущее задание, с которым вы все хорошо справились от этого? (В предыдущем задании дроби были с одинаковыми знаменателями, и у нас был алгоритм сложения таких дробей, а в последнем задании у дробей разные знаменатели). – Что же нам надо сделать, чтобы выполнить задание, определить, кто его выполнил правильно? (Надо найти способ нахождения суммы дробей с разными знаменателями, построить для таких дробей алгоритм сложения). – Сформулируйте цели урока. (Построить алгоритм сложения дробей с разными знаменателями, научиться выполнять действия по построенному алгоритму). – Хорошо! Чтобы продолжить работу, надо записать тему урока, что мы запишем в тетрадь? (Сложение дробей с разными знаменателями.) – Запишите тему. (На доске открывается тема урока).
|
…(необходимо повторить уже изученный материал).
-к 24, т.к. 24 – НОК всех знаменателей.
- проговаривают алгоритм сложения дробей с одинаковыми знаменателями | 12 мин.
|
| 1.3 | Фиксация затруднений |
| Работа в группах: Предлагаю поработать в группах. Ваши результаты не забудьте прикрепить на доску. Время выполнения: 5 минут. Закрасьте указанные части прямоугольника разным цветом. Какая часть закрашена? а) + = 
б) + = 
Затем предлагаю выполнить задания без закрашивания частей: а) + ; б) + . (После завершения работы защита своих работ). Выявление места и причины затруднения. – Почему у вас получились такие разные ответы, как выяснить, кто выполнил задание правильно, а кто-то совсем не дал ответы, чем отличается предыдущее задание, с которым вы все хорошо справились от этого?
– Что же нам надо сделать, чтобы выполнить задание, определить, кто его выполнил правильно?
Сформулируйте цели урока.
Хорошо! Чтобы продолжить работу, надо записать тему урока, что мы запишем в тетрадь?
| Каждая группа показывает свои результаты работы. Проводим обсуждение. Приходим к выводу о том, что результат суммы дробей является частью этого же прямоугольника.
-В предыдущем задании дроби были с одинаковыми знаменателями, и у нас был алгоритм сложения таких дробей, а в последнем задании у дробей разные знаменатели.
-Надо найти способ нахождения суммы дробей с разными знаменателями, построить для таких дробей алгоритм сложения.
- Построить алгоритм сложения дробей с разными знаменателями, научиться выполнять действия по построенному алгоритму.
- Сложение дробей с разными знаменателями.
| 10 мин
|
|
2.1
|
Первичное закрепление во внешней речи
|
|
II.Операционно-познавательная часть Ученики решают у доски, используя алгоритм (обратить внимание на проговаривание). Стр. 194 № 880 (а, б) а) + Приведём дроби к наименьшему общему знаменателю, для этого найдём НОК (2; 4) НОК (2; 4) = 4 Дополнительный множитель первой дроби - 2, второй дроби - 1. + = + Применим алгоритм сложения дробей с одинаковыми знаменателями, складываем числители, знаменатели оставляем без изменения + = + = = Дробь правильная, выделять из неё целую часть не нужно. (б) Проводим аналогичные рассуждения. + = + = =
Физкультминутка Работа в парах, после выполнения проводится самопроверка по образцу (слайд). Каждой паре выдается карточка с заданиями. Урок длится часа, а перемена - часа. Какую часть часа длятся урок с переменой? Рабочий в первый день выполнил , а во второй - всего заказа. Какую часть заказа сделал рабочий за два дня? Туристы прошли до привала пути, после привала – еще пути. Какую часть пути они прошли? - Кто справился с заданием? Где допущена ошибка? - Повторим ещё раз алгоритм сложения дробей с разными знаменателями.
|
Ученик решает на доске, остальные в тетрадях
|
5 мин.
2 мин.
3 мин. |
| 2.2 | Самостоятельная работа с проверкой по эталону |
|
1. Выполните действия: (обязательные задания для всех) а) + = + = = . б) + = + = = = 8. 2. Сравните значения выражений: а) + и + б) + + и + + ( дополнительное задание для сильных учеников) А сейчас каждый проверит сам себя – насколько он сам понял алгоритм сложения и может его применить. (ЦОР- тест) с проверкой и самооценкой |
После выполнения работы учащиеся проверяют свои ответы и отмечают правильно решённые примеры, исправляют допущенные ошибки, проводится выявление причин допущенных ошибок.
| 5 мин. |
| Ш Рефлексивно- оценочная часть |
| 3.1 | Рефлексия деятельности на уроке |
| – Что нового узнали на уроке? – Какую цель мы ставили в начале урока? – Наша цель достигнута? – Что нам помогло справиться с затруднением? – Какие знания нам пригодились при выполнении заданий на уроке? – Как вы можете оценить свою работу?
|
| 2 мин. |
| 3.2 | Задание на дом |
| алгоритм учить (раздать каждому), № 882(а - г), № 883. |
| 1 мин. |




















