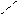Урок математики по теме "Пирамида"
Цель урока: формирование представления о пирамиде и навыков применения формулы нахождения площади поверхности и построения сечения при решении несложных задач.
Задачи:
- образовательные (формирование познавательных УУД):
использование определения следующих понятий: «пирамида», «площадь боковой поверхности пирамиды», «площадь полной поверхности пирамиды» в процессе реальной ситуации; использование свойств пирамиды и строение сечения.
- воспитательные (формирование коммуникативных и личностных УУД):
умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, воспитывать ответственность и аккуратность.
- развивающие (формирование регулятивных УУД)
развитие умений анализировать, сравнивать, обобщать, делать выводы, развивать внимание, формировать коммуникативную компетенцию учащихся, последовательность действий при решении задач в зависимости от конкретных условий, трудолюбия; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.
Тип урока: усвоение новых знаний.
План урока:
Организационный момент.
Актуализация знаний.
Изучение нового материала.
Решение простейших задач.
Рефлексия.
Домашнее задание.
Оборудование: компьютер, мультимедийный проектор, презентация.
Ход урока:
1. Организационный момент.
Сегодня мы совершим путешествие во времени.
Слайд1 Фараон Джосер повелел создать для себя необычную гробницу, похожую на гигантскую каменную лестницу, по которой фараон после смерти должен был подняться на небо. Его замысел воплотил в жизнь великий египетский зодчий Имхотеп. Правившие после Джосера фараоны тоже строили себе ступенчатые пирамиды, пока фараону Снофру не пришла в голову мысль выстроить для своей гробницы не ступенчатую, а гладкую пирамиду.
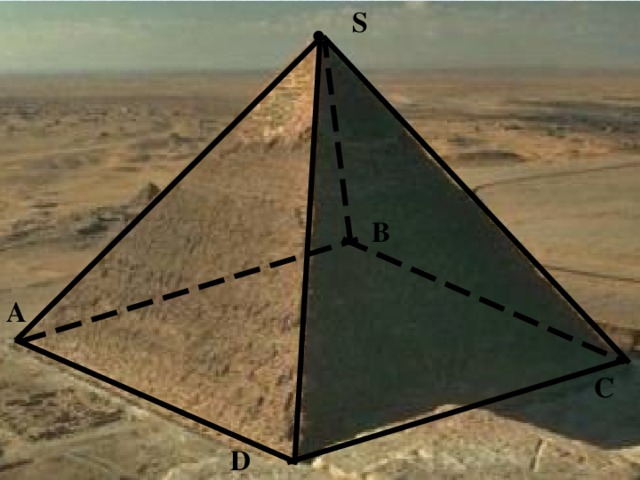
Слайд2 Вслед за Снофру Древним Египтом правил его сын, фараон Хуфу, или, как мы его привыкли называть, - Хеопс. За 23 года своего правления он сумел выстроить самую грандиозную и удивительную пирамиду, которую мы называем первым чудом света.
Пирамиды – самое грандиозное из всех чудес света. Построенная около 2600 г. до н.э., она имеет высоту 146 метров, состоит из 2300000 каменных блоков, каждый весом примерно 3 тонны.
Даже сегодня при современных машинах и механизмах выстроить такую громадную пирамиду было бы нелегко.
Но мы сегодня должны научиться строить пирамиды.
2. Актуализация знаний.
Термин «пирамида» заимствован из греческого «пирамис» или «пирамидос». Греки в свою очередь позаимствовали это слово из египетского языка. В папирусе Ахмеса встречается слово «пирамис» в смысле ребра правильной пирамиды. Другие считают, что термин берет свое начало от формы хлебцев в Древней Греции («пирос» - рожь). В связи с тем, что форма пламени напоминает образ пирамиды, некоторые ученые считали, что термин происходит от греческого слова «пир» - огонь.
Итак, тема урока “Пирамида”.
Мы с вами рассмотрим пирамиду с математической точки зрения.
Что мы можем узнать о пирамиде? Познакомиться с понятием пирамида, ее видами, элементами, свойствами, решить простейшие задачи.
Итак, цель урока: изучить новый вид многогранников – пирамиды. Рассмотреть задачи, связанные с пирамидой.
- Опишите фигуры, изображенные на Слайде3 (основание, вершина, ребра)
- Что объединяет эти тела? (в основании n-угольник, боковые грани – треугольники).
- Как можно назвать эти тела? (пирамиды)
Итак, пирамидой называется многогранник, который состоит из плоского многоугольника – основание пирамиды; точки, не лежащей в плоскости основания – вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания – боковыми ребрами.
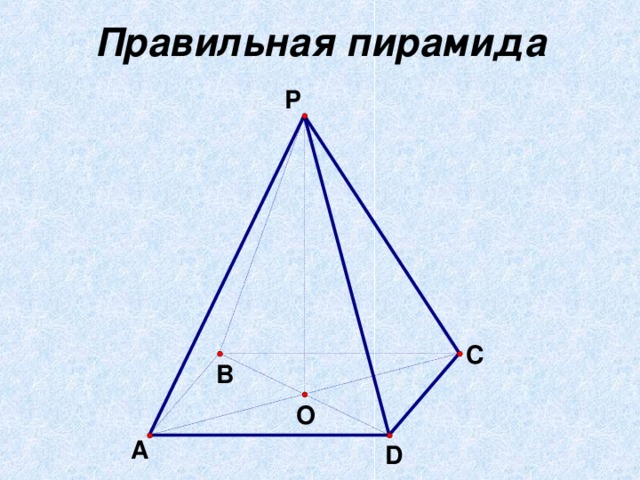
- Слайд4 Дайте определение высоты пирамиды. (Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания).
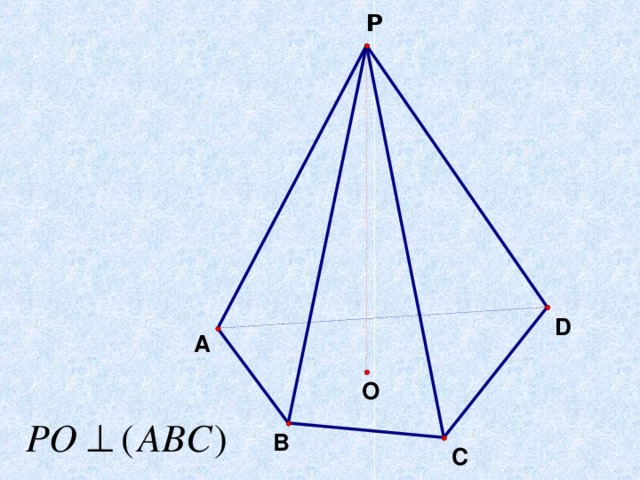
- Слайд5 Что это за многогранник? Дайте определение тетраэдра (поверхность, состоящая из четырех правильных треугольников или многогранник, состоящий их четырех треугольников)
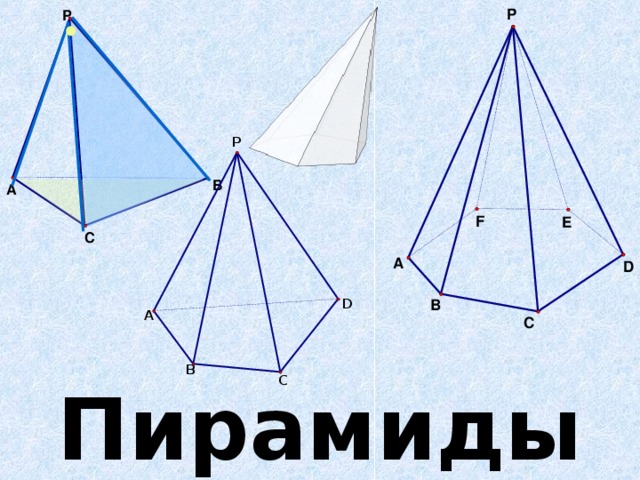
- Слайд6 Пирамида называется правильной, если её основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является её высотой.
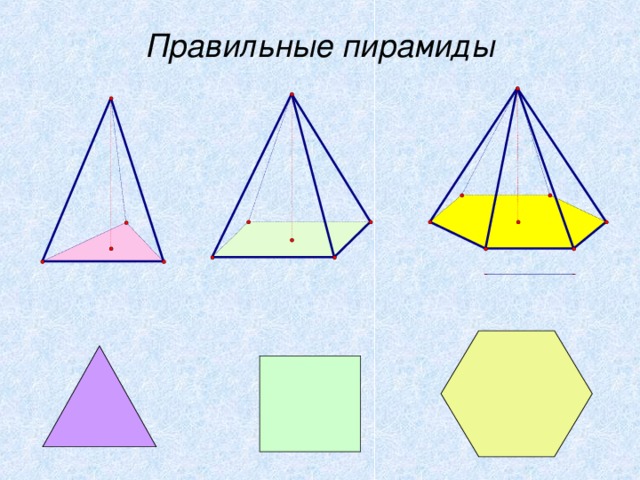
- Слайд7 Какие пирамиды могут быть правильными? (в основании лежит правильный треугольник – треугольная пирамида, в основании лежит квадрат - четырехугольная пирамида, в основании лежит правильный шестиугольник – шестиугольная пирамида)
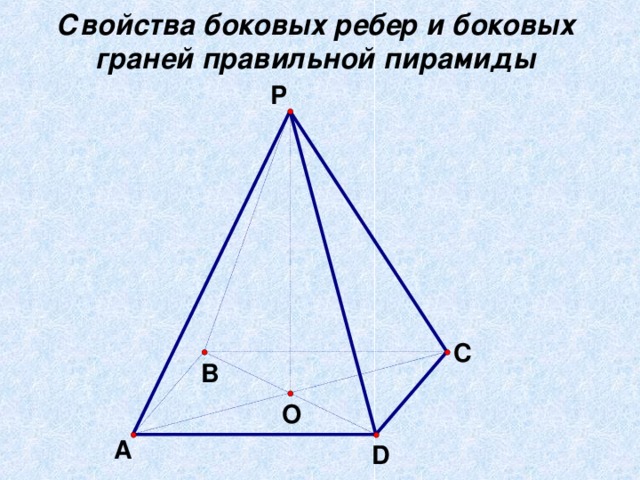
- Слайд8 Свойства боковых ребер и боковых граней правильной пирамиды. (Все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками)
Построим пирамиду Хеопса.
1. Постройка Великих пирамид Хеопса, Хефрена и Микерина требовала огромных усилий всех свободных египтян. Их труд был настоящим чудом. Строители работали с большим энтузиазмом над возведением гробницы своего великого фараона. Они верили: фараон – сын бога, и после смерти он окажется среди богов. Если они выкажут ему подлинное уважение, он позаботится о них, простых людях, об их детях, внуках и правнуках.
Выкажем же и мы ему подлинное уважение. Построим пирамиду Хеопса.
Итак, что лежит в основании пирамиды Хеопса (квадрат)
- Как изображается квадрат на плоскости? (параллелограммом)
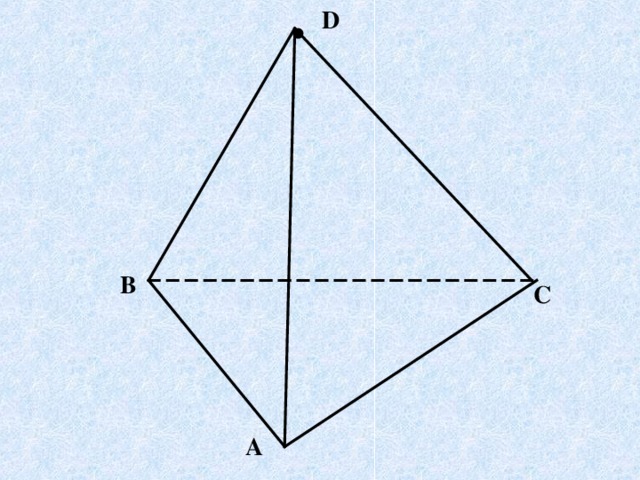
- Слайд9 построим основание,
- отметим вершину параллелограмма,
- соединим вершину боковыми ребрами с вершинами основания.
2. Построим треугольную пирамиду.
- Слайд10 Построим основание,
- отметим вершину параллелограмма,
- соединим вершину боковыми ребрами с вершинами основания.
3. Решение задач.
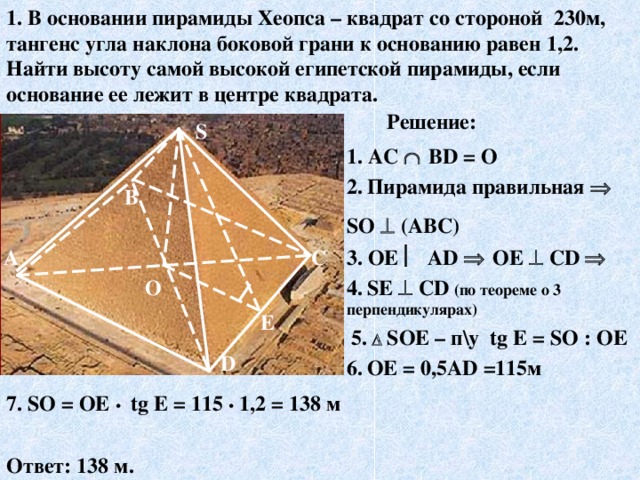
Слайд11 1. В основании пирамиды Хеопса – квадрат со стороной 230м, тангенс угла наклона боковой грани к основанию равен 1,2. Найти высоту самой высокой египетской пирамиды, если основание ее лежит в центре квадрата.
![]()
S


Решение
1. AC Ç ВD = О
2. Пирамида правильная Þ SО ^ (АВС)
3. ОЕ çç АD Þ ОЕ ^ АD Þ
4. SЕ ^ СD (по теореме о 3 перпендикулярах)
Чему равен тангенс острого угла в прямоугольном треугольнике? (отношению противолежащего катета к прилежащему катету)
5. D SОЕ – п\у tg E = SО : ОЕ = 1,2
6. ОЕ = 0,5АD =115м
7. SО = ОЕ • tg E = 1,2 • 115 = 138 м
Ответ: 138м
С
В
Е
![]()
А

О


![]()
230
D
![]()
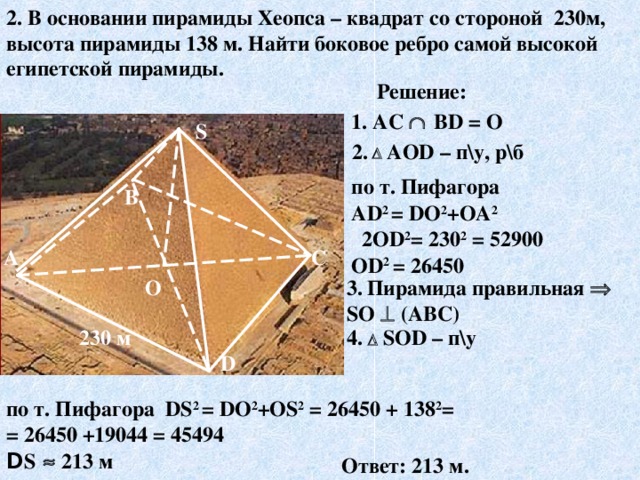
Слайд12 2. В основании пирамиды Хеопса – квадрат со стороной 230м, высота пирамиды 138 м. Найти боковое ребро самой высокой египетской пирамиды. Решение
1. AC Ç ВD = О
2. D АОD – п\у, р\б
по т. Пифагора АD2 = DО2+ОА2
2ОD2= 2302 = 52900
ОD2 = 26450
3. Пирамида правильная Þ SО ^ (АВС)
4. D SОD – п\у
по т. Пифагора DS2 = DО2+ОS2 = 26450 + 1382=
= 26450 +19044 = 45494
DS » 213 м
Ответ: 213м
![]()
S


С
В
А

О


![]()
230
D
![]()
- Слайд13 Из чего состоит поверхность пирамиды? (из основания, и боковых граней)
- Чем является боковая грань? (треугольником)
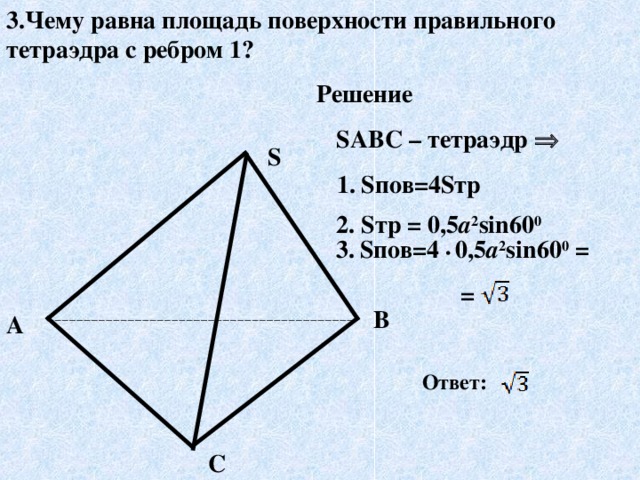
Слайд14 3.Чему равна площадь поверхности правильного тетраэдра с ребром 1?
Решение
1. Sпов=4Sтр
2. Sтр = 0,5а2sin600
3. Sпов= 4 • 0,5а2sin600 =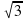
Ответ: 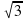
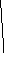



![]()

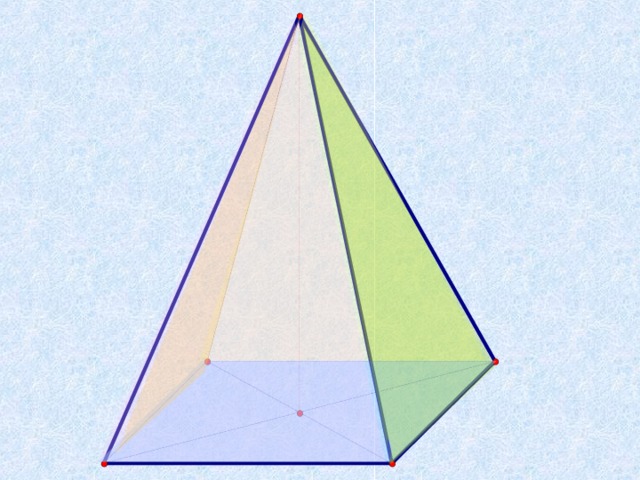
 Слайд15 4. Найдите площадь боковой поверхности пирамиды Хеопса, сторона основания которой равна 230м и высота 138м.
Слайд15 4. Найдите площадь боковой поверхности пирамиды Хеопса, сторона основания которой равна 230м и высота 138м. Решение
1. Sб.пов=4Sтр
2. AC Ç ВD = О
3. Пирамида правильная Þ
SО ^ (АВС)
4. ОЕ çç СD Þ ОЕ ^ АD Þ
5. SЕ ^ АD (по теореме о 3 перпендикулярах)
6. ЕОS- п\у по т. Пифагора ЕS2 = ЕО2+ОS2 = 1152 + 1382 =
= 13225 +19044 = 32269
ЕS 180
7. ES - высота АSD
SАSD = 0,5 ЕS•АD 0,5 •180 • 230 20700 м2
8. Sб.пов=4Sтр 4 • 20700 82800 м2
Ответ: 82800 м2
S
С
В
138
О


![]()
230
Е
D
А
![]()
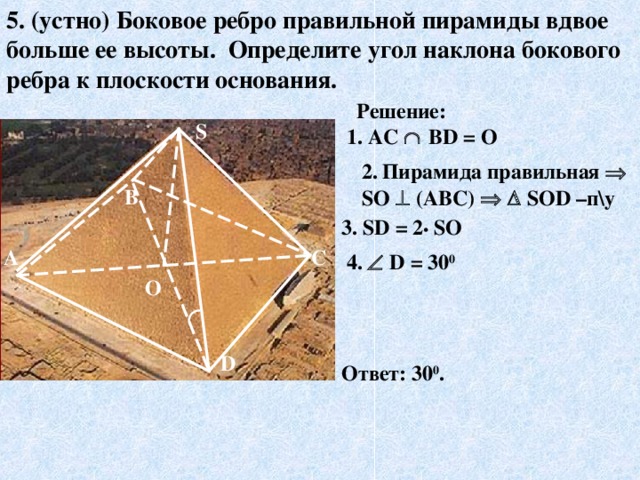
Слайд16 5. (устно) Боковое ребро правильной пирамиды вдвое больше ее высоты. Определите угол наклона бокового ребра к плоскости основания. (300)

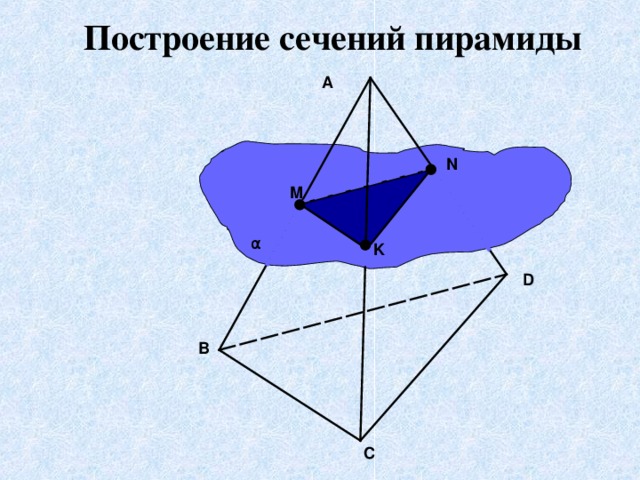
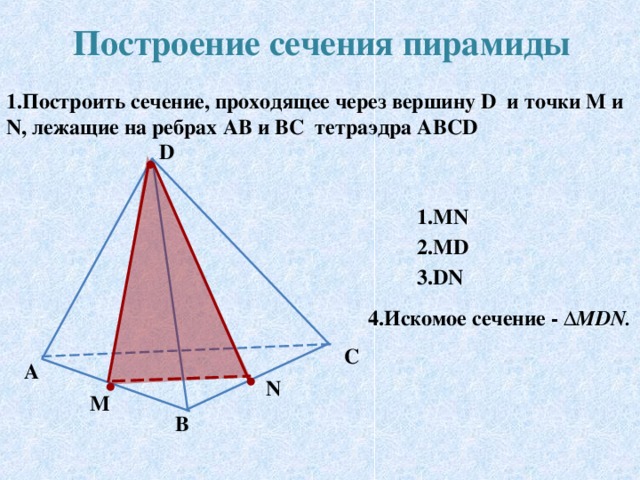
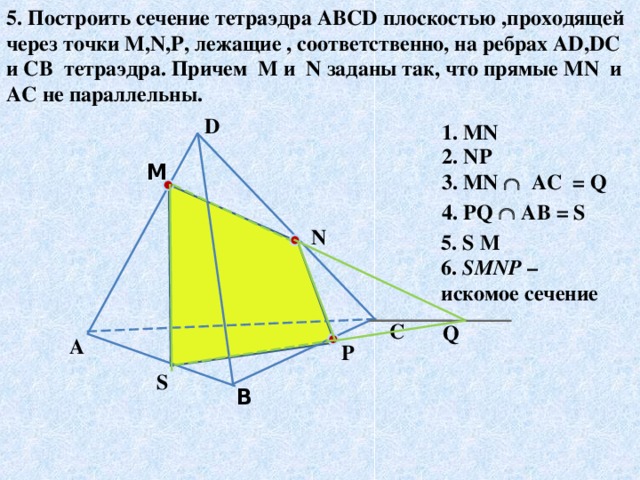
Построение сечений пирамиды. Слайд17
Перед учащимися ставится задача, в ходе решения которой повторяются основные аксиомы и теоремы. Осуществляется пошаговая проверка построения сечения.
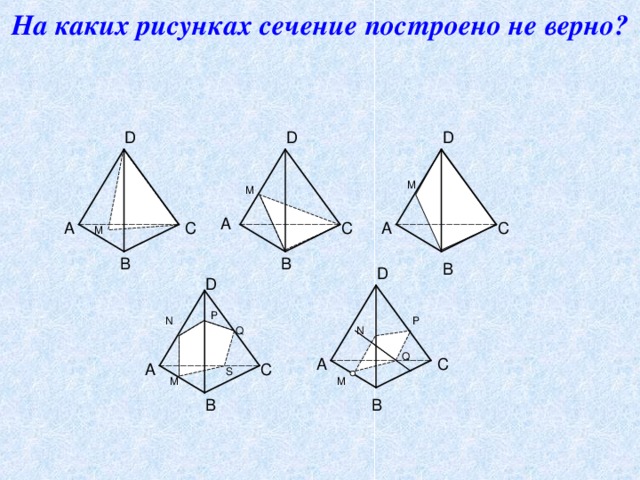
Слайд18 - На каких рисунках сечение построено не верно? (1, 3, 4)

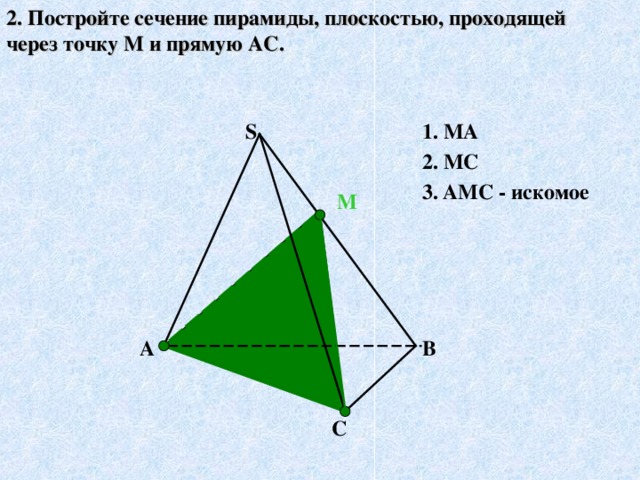
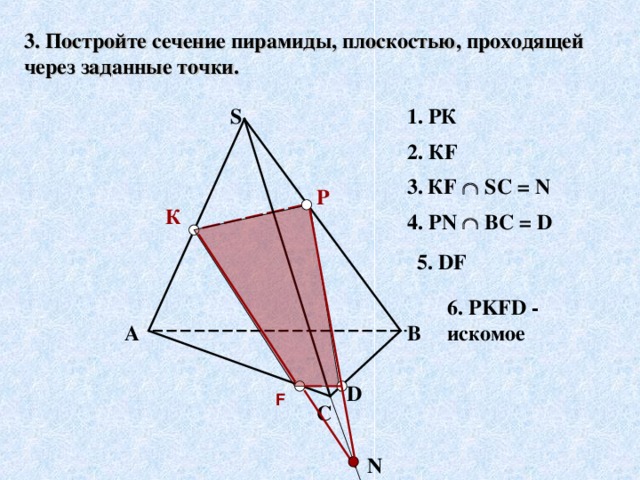
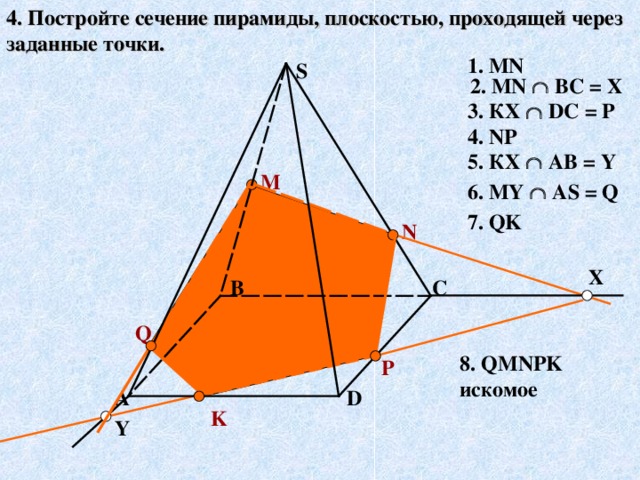
Задачи Слайд19 - 23

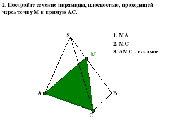
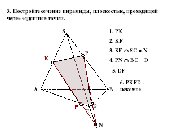
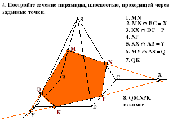
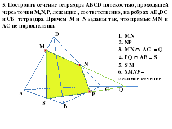
Рефлексия.
Подведем итоги нашей совместной работы.
Выставление оценок.
Что нового узнали на сегодняшнем уроке?
Какие знания пригодились?
Что было сложного?
Что понравилось на уроке?
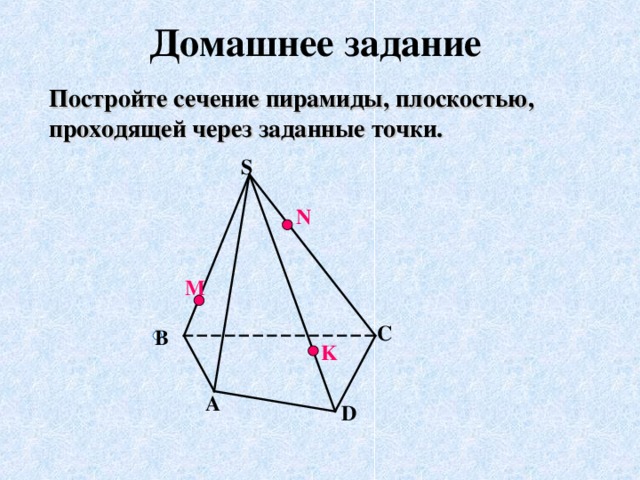
5. Домашнее задание.
1). Если в правильной треугольной пирамиде высота H равна стороне основания a, то боковые ребра составляют с плоскостью основания углы в 600. Верно ли это утверждение?
2). Сторона квадрата равна 10 см. Доказать, что нельзя, используя его в качестве основания, построить правильную четырехугольную пирамиду с боковым ребром 7 см.
3). Доказать или опровергнуть утверждение: «если в пирамиде все ребра равны, то пирамида правильная».
4). 





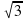




 Слайд15 4. Найдите площадь боковой поверхности пирамиды Хеопса, сторона основания которой равна 230м и высота 138м.
Слайд15 4. Найдите площадь боковой поверхности пирамиды Хеопса, сторона основания которой равна 230м и высота 138м.