Разработка урока математики по теме: «Степень числа». 5 класс.
Тема: «Степень числа»
Тип урока: Урок усвоения новых знаний.
Цель урока:
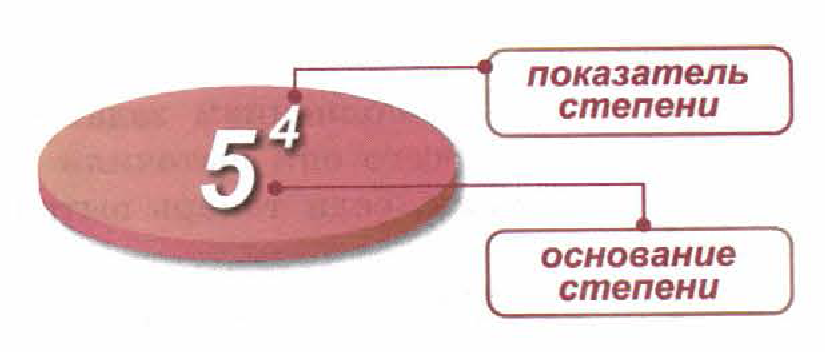
- Знать: определение степени; понятия – «основание степени », «показатель степени ».
- Уметь: находить числовое значение степени, определять порядок действий и находить значения числовых выражений, содержащих степень.
Структура урока:
1. Организационный.
2. Актуализация знаний и умений.
3. Постановка цели урока.
4. Усвоение нового материала.
5. Первичное закрепление
6. Первичный контроль
7. Подведение итогов урока.
8. Информация о домашнем задании.
Ход урока.
1. Актуализация знаний.
Мы закончили изучение темы «Порядок действий в выражениях»:
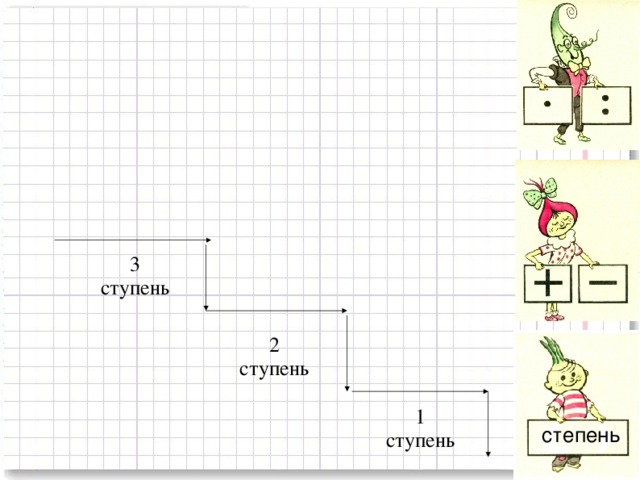
- Какие действия называются действиями первой ступени?
- Какие действия называются действиями второй ступени?
- Как вы думаете, а существуют ли действия третьей ступени?
- Как выполняются действия в выражениях со скобками?
- Как выполняются действия в выражениях без скобок?
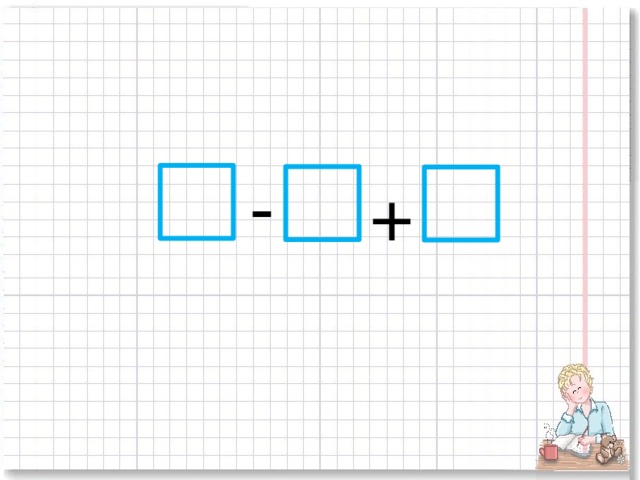
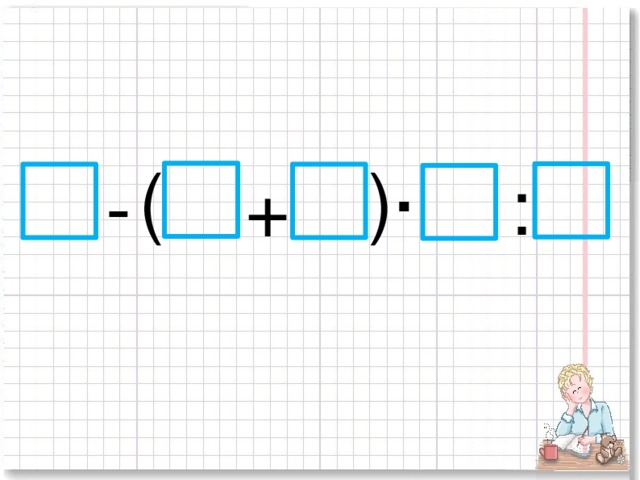
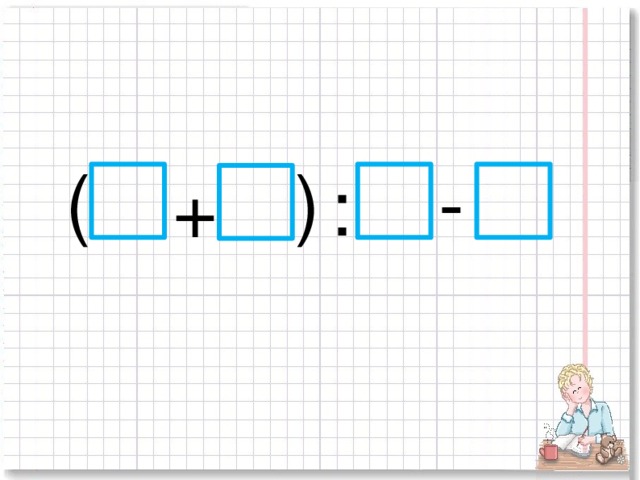
Давайте посмотрим, насколько хорошо мы ее усвоили. Игра «Баскетбол» (слайд №1)
- Какое действие в данных выражениях будет последним? (Каждый учащийся передает ход другому, подсчитываются очки).
Итак, со счетом … команда 5Б класса выиграла у команды «Порядок действий в выражениях»
2. Постановка цели урока. Изучение нового материала.
Выход на тему и цель урока: «Степень числа». Включение учащихся в самостоятельную работу по алгоритму.
Следующее задание: Найдите лишнее (слайд №2) (Учащиеся находят лишнее выражение 5∙5∙5∙5) Вот о таких выражениях у нас сегодня будет идти речь.
Посмотрите на выражения (слайд №3). Что в них общего? В чем различие? Можете ли вы продолжить? Сколько множителей будет в 10-ом ряду? Сколько в 45-ом? В 100-ом? Запишите, пожалуйста, выражение, которое получится в 1000-ом ряду? Не сможете? Почему? Слишком долго и слишком много требуется места? А какие у вас будут предложения по этому поводу? Мы умеем короче записывать сумму нескольких одинаковых слагаемых (в виде произведения). Можно предположить, что и произведение нескольких множителей тоже можно записать короче.
Итак, темой нашего урока сегодня будет произведение, в котором все множители равны друг другу. Какие задачи стоят перед нами? (Узнать, как называется произведение одинаковых множителей, как оно записывается короче, как читается, что означают числа в такой записи и как они называются, как вычислять выражения с таким произведением. А зачем все это знать? Чтобы научиться вычислять выражения, содержащие такие произведения одинаковых множителей). А как сформулировать нашу тему покороче расскажите мне вы после того, как выполните первое задание в рабочем листе.
РАБОТАЕМ С ТЕКСТОМ.
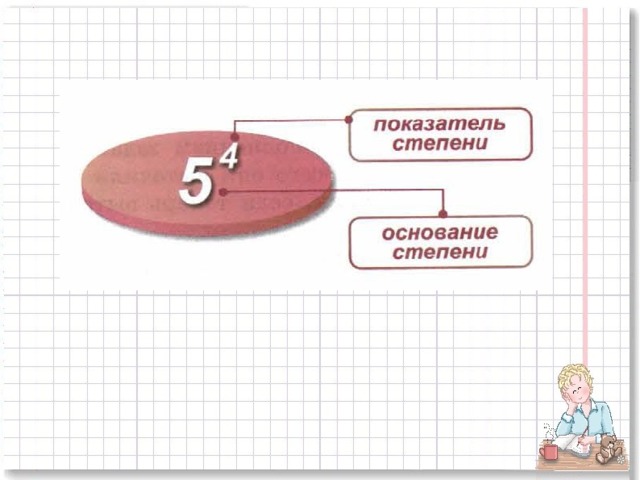
Найдите и прочитайте в учебнике на с.98 текст, в котором объясняется, что означает выражение 26. Вставьте в следующий текст пропущенные слова:
«Выражение 26 означает произведение ___________________ множителей, каждый из которых равен ____________, называют _____________________ и читают так: два в ___________________________. В этом выражении число 2 - ___________________, а число 6 - ________________________.
Основание степени - это ________________________________________, а показатель _____________________________________________________________________.
Примеры:
1. В выражении 34 число __________ - основание степени, число ___________________ - показатель степени.
2. У степени _____________ основание равно 5, а показатель равен 3».
Какое из следующих выражений можно записать в виде степени 67?
6 + 6 + 6 + 6 + 6 + 6 + 6
7 ∙ 7 ∙ 7 ∙ 7 ∙ 7 ∙ 7
6 ∙ 6 ∙ 6 ∙ 6 ∙ 6 ∙ 6 ∙ 6
6 ∙ 7
Заполните таблицу.
| Произведение | Степень | Основание степени | Показатель степени |
|
|
| 7 | 5 |
|
| 32 |
|
|
| 4 ∙ 4 ∙ 4 |
|
|
|
Прочитайте текст.


Первичное закрепление.
ОСВАИВАЕМ АЛГОРИТМЫ.
1.Запишите выражение и найдите его значение:
а) три в пятой степени
б) пять в третьей степени
в) семь в квадрате
г) шесть в кубе
Закончите равенство:
53 = 5 ∙ 5 ∙ 5
95 =
26 =
а4 =
b2 =
Выполните возведение в степень:
22 = 2∙2 = 4 03 =
52 = 33 =
122 = 43 =
72 = 13 =
Прочитайте правило вычисления выражений, содержащих степени и выполните действия:

Сравните:
13 __12
23 __2 + 2 + 2
14 __1 + 1 + 1 + 1
25 __52
13 + 23__(1 + 2)3
Найдите значение выражения:
а) 3 ∙ 42 = ________
б) (3 ∙ 2)2 = ________
в) 27 : 32 = ________
г) 250 : 53 = ________
д) (76 - 66)3∙18 = ________
е) 600 – 750 : 53 = ________
2. АНАЛИЗИРУЕМ И РАССУЖДАЕМ
Сережа невнимательно выполнил домашнюю работу и в каждом задании сделал ошибку. Найдите ошибки в Сережиных решениях.
| Задание | Сережино решение | Правильное решение |
| 5 ∙ 202 | 5 ∙ 20 ∙ 2 = 200 |
|
| (4 ∙ 3)2 – 4 ∙ 32 | 122 - 122 = 12 ∙ 12 – 12 ∙ 12 = = 144 – 144 = 0 |
|
| 63 : 3 | (6 : 3)3 = 23 = 2 ∙ 2 ∙ 2 = 8 |
|
4. Первичный контроль
1.Выполните САМОСТОЯТЕЛЬНУЮ РАБОТУ.
2.Проверьте правильность решения по ключу. Оцените работу.
САМОСТОЯТЕЛЬНАЯ РАБОТА
Запишите выражение и найдите его значение
а) три в четвертой степени ___________ а) два в пятой степени ______________
б) восемь в квадрате ________________ б) пять в кубе _____________________
Сравните значения выражений
53 __ 35 44 __ 82
Найдите значение выражений
а) 16 + 42 а) 33 – 33
б) 42 – 122 : 4 б) 2 ∙ 152 + 5
5. Подведение итогов

Задание на дом.
П. 16, №666, 668 (а-д), 669
Литература:
1.Дорофеев Г.В. и др. Математика: Учебник для 5 кл., Москва «Просвещение», 1996.
2. Дорофеев Г.В. и др. Дидактические материалы для 5 кл., Москва «Просвещение», 2001.
3. Бунимович Е.А. и др. Математика: Рабочая тетрадь для 5 кл., Москва «Просвещение»,2001.








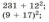
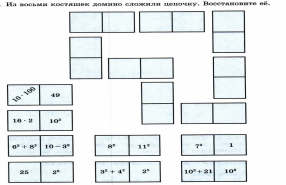





 8 2 3 . а) 6 б) 455" width="640"
8 2 3 . а) 6 б) 455" width="640"